第20章-隐马尔可夫模型--机器学习与应用第二版
- 格式:pdf
- 大小:482.48 KB
- 文档页数:15

隐马尔可夫模型原理
隐马尔可夫模型(Hidden Markov Model, HMM)是一种用来
描述状态序列的概率模型。
它基于马尔可夫链的理论,假设系统的状态是一个没有直接观察到的随机过程,但可以通过观察到的结果来推断。
HMM的原理可以分为三个关键要素:状态集合、转移概率矩
阵和观测概率矩阵。
1. 状态集合:HMM中的状态是不能直接观测到的,但可以从
观测序列中推断出来。
状态集合可以用S={s1, s2, ..., sn}表示,其中si表示第i个状态。
2. 转移概率矩阵:转移概率矩阵A表示在一个时间步从状态
si转移到状态sj的概率。
可以表示为A={aij},其中aij表示从状态si到状态sj的转移概率。
3. 观测概率矩阵:观测概率矩阵B表示在一个时间步观测到
某个输出的概率。
可以表示为B={bj(o)},其中bj(o)表示在状
态sj下观测到输出o的概率。
通过这些要素,HMM可以用来解决三类问题:
1. 评估问题:给定模型参数和观测序列,计算观测序列出现的概率。
可以使用前向算法或后向算法解决。
2. 解码问题:给定模型参数和观测序列,寻找最可能的状态序
列。
可以使用维特比算法解决。
3. 学习问题:给定观测序列,学习模型的参数。
可以使用Baum-Welch算法进行无监督学习,或使用监督学习进行有标注数据的学习。
总之,HMM是一种可以用来描述随机过程的模型,可以用于许多序列预测和模式识别问题中。
它的简洁性和可解释性使其成为机器学习领域中重要的工具之一。

隐马尔可夫模型算法
隐马尔可夫模型算法是一种用于序列数据分析的统计模型,它可以用来预测未来的状态或者根据已知的状态推断出隐藏的状态。
这种模型在自然语言处理、语音识别、生物信息学等领域都有广泛的应用。
隐马尔可夫模型算法的基本思想是,将一个系统看作是由一系列状态组成的,每个状态都有一个对应的观测值。
这些状态之间的转移是随机的,而观测值则是由状态生成的。
因此,我们可以通过观测值来推断出隐藏的状态,或者根据已知的状态来预测未来的观测值。
在隐马尔可夫模型算法中,我们需要定义两个概率分布:状态转移概率和观测概率。
状态转移概率指的是从一个状态转移到另一个状态的概率,而观测概率则是在某个状态下观测到某个观测值的概率。
这些概率可以通过训练数据来估计,通常使用最大似然估计或者贝叶斯估计。
隐马尔可夫模型算法的核心是前向-后向算法和维特比算法。
前向-后向算法用于计算给定观测序列下,某个状态出现的概率。
维特比算法则用于寻找最可能的状态序列,即给定观测序列下,最可能的状态序列。
隐马尔可夫模型算法的应用非常广泛。
在自然语言处理中,它可以用于词性标注、命名实体识别、机器翻译等任务。
在语音识别中,
它可以用于声学模型的建立。
在生物信息学中,它可以用于DNA序列分析、蛋白质结构预测等任务。
隐马尔可夫模型算法是一种非常强大的序列数据分析工具,它可以用于各种领域的任务。
虽然它的理论比较复杂,但是在实际应用中,我们可以使用现有的库或者工具来实现它,从而更加方便地应用它。



机器学习的马尔科夫模型研究及应用一、背景介绍机器学习是人工智能领域中的一个重要分支,主要是为了让计算机系统具有自主学习和自我优化的能力。
当前,机器学习在语音识别、图像识别、自然语言处理等方面已有广泛应用。
而马尔科夫模型是机器学习中的一种重要算法,具有广泛应用前景。
本文会介绍马尔可夫模型的概念、特点以及其在机器学习中的应用。
二、马尔科夫模型概念1.定义马尔科夫模型是一种描述在时间序列中某一状态的概率转移模型。
具体说来,马尔科夫模型假设一个系统,状态在时间变化中具有马尔科夫性质,也就是说,这个状态在下一时刻仅依赖于当前时刻的状态,而与其他时刻的状态无关。
因而可以用状态及其之间的概率关系来描述这个系统。
2.特点马尔科夫模型的特点是:(1) 马尔科夫模型的输出是未来状态的概率分布。
(2) 马尔科夫模型假设未来状态的概率分布仅由当前状态决定。
(3) 马尔科夫模型具有可逆性。
三、马尔科夫模型应用1.自然语言处理马尔科夫模型可以应用于自然语言处理方面。
在构建语言模型时,可以用马尔科夫模型描述自然语言的语法和动态特性。
在语言模型中,马尔科夫模型通常被用来描述一个原文与其翻译之间的对应关系。
2.机器翻译机器翻译是利用计算机程序进行的自然语言翻译。
马尔科夫模型是机器翻译中一个重要的方法。
具体来说,马尔科夫模型用于描述原文与翻译之间的概率转移关系,并通过最大似然估计算法来计算出最优参数。
3.语音识别语音识别是将口语语音转化成电脑可读写的文本的一种技术。
马尔科夫模型已经被广泛应用于语音识别领域。
马尔科夫模型主要描述语音的语调、语速、声音强度等因素。
语音识别系统可以通过计算最大似然概率来对输入的语音进行识别。
四、机器学习马尔科夫模型应用1.隐马尔科夫模型隐马尔科夫模型(HMM)是一种常见的马尔科夫模型。
HMM的特点是,输出序列不是可观测的,而是被一个隐藏的状态序列控制的。
HMM主要用于序列问题如语音识别、自然语言处理等。

隐马尔科夫模型(Hidden Markov Model, HMM)是一种用来建模含有隐藏状态的系统的概率模型,它在语音识别、自然语言处理、生物信息学等领域都有着广泛的应用。
近年来,隐马尔科夫模型在教育领域中的应用也逐渐引起了人们的关注。
本文将从教育领域使用隐马尔科夫模型的技巧展开讨论。
首先,隐马尔科夫模型在教育领域中可以用来分析学生的学习情况。
通过收集学生的学习行为数据,如阅读时间、作业完成情况、课堂表现等,可以建立一个隐马尔科夫模型来对学生的学习状态进行建模。
这样一来,教师可以根据模型的输出来了解学生的学习情况,及时发现学生的学习问题并进行干预,提高教学效果。
其次,隐马尔科夫模型还可以用来进行学生学习行为的预测。
通过历史的学习行为数据,可以建立一个隐马尔科夫模型来预测学生未来的学习状态。
这样一来,教师可以提前知晓学生可能的学习状态,有针对性地进行教学准备,提高教学效率。
另外,隐马尔科夫模型还可以用来进行学生学习能力的评估。
通过收集学生的学习行为数据,可以建立一个隐马尔科夫模型来对学生的学习能力进行评估。
这样一来,教师可以根据模型的输出来评估学生的学习能力,有针对性地进行教学安排,帮助学生提高学习效果。
除此之外,隐马尔科夫模型还可以用来进行课程设计与优化。
通过收集学生的学习行为数据,可以建立一个隐马尔科夫模型来对课程进行建模。
这样一来,教师可以根据模型的输出来对课程进行优化,提高课程的教学效果。
综上所述,隐马尔科夫模型在教育领域中有着广泛的应用前景。
通过对学生的学习行为数据进行建模,可以帮助教师更好地了解学生的学习情况,并有针对性地进行教学。
隐马尔科夫模型的应用将极大地提高教育领域的教学效果,推动教育事业的发展。
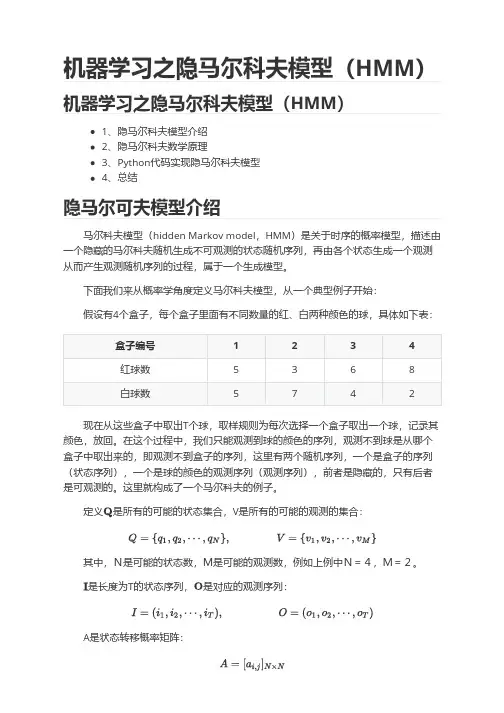
机器学习之隐马尔科夫模型(HMM)机器学习之隐马尔科夫模型(HMM)1、隐马尔科夫模型介绍2、隐马尔科夫数学原理3、Python代码实现隐马尔科夫模型4、总结隐马尔可夫模型介绍马尔科夫模型(hidden Markov model,HMM)是关于时序的概率模型,描述由一个隐藏的马尔科夫随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程,属于一个生成模型。
下面我们来从概率学角度定义马尔科夫模型,从一个典型例子开始:假设有4个盒子,每个盒子里面有不同数量的红、白两种颜色的球,具体如下表:盒子编号1234红球数5368白球数5742现在从这些盒子中取出T个球,取样规则为每次选择一个盒子取出一个球,记录其颜色,放回。
在这个过程中,我们只能观测到球的颜色的序列,观测不到球是从哪个盒子中取出来的,即观测不到盒子的序列,这里有两个随机序列,一个是盒子的序列(状态序列),一个是球的颜色的观测序列(观测序列),前者是隐藏的,只有后者是可观测的。
这里就构成了一个马尔科夫的例子。
定义是所有的可能的状态集合,V是所有的可能的观测的集合:其中,N是可能的状态数,M是可能的观测数,例如上例中N=4,M=2。
是长度为T的状态序列,是对应的观测序列:A是状态转移概率矩阵:其中, 是指在时刻处于状态的条件下在时刻转移到状态的概率。
B是观测概率矩阵:其中, 是指在时刻处于状态的条件下生成观测的概率。
是初始状态概率向量:其中, 是指在时刻=1处于状态的概率。
由此可得到,隐马尔可夫模型的三元符号表示,即称为隐马尔可夫模型的三要素。
由定义可知隐马尔可夫模型做了两个基本假设:(1)齐次马尔科夫性假设,即假设隐藏的马尔科夫链在任意时刻的状态只和-1状态有关;(2)观测独立性假设,观测只和当前时刻状态有关;仍以上面的盒子取球为例,假设我们定义盒子和球模型:状态集合: = {盒子1,盒子2,盒子3,盒子4}, N=4观测集合: = {红球,白球} M=2初始化概率分布:状态转移矩阵:观测矩阵:(1)转移概率的估计:假设样本中时刻t处于状态i,时刻t+1转移到状态j 的频数为那么转台转移概率的估计是:(2)观测概率的估计:设样本中状态为j并观测为k的频数是那么状态j观测为k的概率, (3)初始状态概率的估计为S个样本中初始状态为的频率。


隐藏式马尔可夫模型及其应用随着人工智能领域的快速发展,现在越来越多的数据需要被处理。
在这些数据中,有些数据是难以被观察到的。
这些难以被观察到的数据我们称之为“隐藏数据”。
如何对这些隐藏数据进行处理和分析,对于我们对这些数据的认识和使用有着至关重要的影响。
在这种情况下,隐马尔可夫模型就显得非常重要了。
隐马尔可夫模型(Hidden Markov Model,HMM)是一种非常重要的统计模型,它是用于解决许多实际问题的强有力工具。
该模型在语音识别、自然语言处理、生物信息学、时间序列分析等领域都有广泛应用。
隐马尔可夫模型是一种基于概率的统计模型。
该模型涉及两种类型的变量:可见变量和隐藏变量。
可见变量代表我们能够观察到的序列,隐藏变量代表导致可见序列生成的隐性状态序列。
HMM 的应用场景非常广泛,如基因组序列分析、语音识别、自然语言处理、机器翻译、股票市场等。
其中,最常见和经典的应用场景之一是语音识别。
在语音识别过程中,我们需要将输入的声音转换成文本。
这里,语音信号是一个可见序列,而隐藏变量则被用来表示说话人的音高调整、语速变化等信息。
HMM 的训练过程旨在确定模型的参数,以使得模型能够最佳地描述观察到的数据。
在模型训练中,需要对模型进行无监督地训练,即:模型的训练样本没有类别信息。
这是由于在大多数应用场景中,可收集到的数据往往都是无标注的。
在语音识别的任务中,可以将所需的标签(即对应文本)与音频文件一一对应,作为主要的训练数据。
我们可以利用EM算法对模型进行训练。
EM算法是一种迭代算法,用于估计最大似然和最大后验概率模型的参数。
每次迭代的过程中使用E步骤计算期望似然,并使用M步骤更新参数。
在E步骤中,使用当前参数计算隐藏状态的后验概率。
在M步中,使用最大似然或者最大后验概率的方法计算参数更新值。
这个过程一直进行到模型参数收敛为止。
总的来说,隐马尔可夫模型是一种非常强大的工具,能够应用于许多领域。
隐马尔可夫模型的应用必须细心,仔细考虑数据预处理、模型参数的选择和训练等问题。

隐马尔可夫模型的步骤
隐马尔可夫模型(HiddenMarkovModel)是一种描述序列数据的统计模型。
它的应用范围很广,例如语音识别、自然语言处理、生物信息学等领域。
下面是隐马尔可夫模型的步骤:
1. 确定模型参数:隐马尔可夫模型包括状态转移概率矩阵A、发射概率矩阵B和初始状态概率向量π。
这些参数需要通过训练数据进行估计。
2. 确定观测序列:观测序列是模型要处理的数据,通常用符号序列表示,例如语音信号的频率、文本中的单词等。
3. 定义状态空间:状态空间是指模型中所有可能的状态的集合。
每个状态都对应着一个观测值或一组观测值。
4. 确定状态转移概率矩阵A:状态转移概率矩阵A描述了模型中状态之间的转移概率。
对于每个状态,它可以转移到自身或其他状态。
通过训练数据,可以估计出不同状态之间的转移概率。
5. 确定发射概率矩阵B:发射概率矩阵B描述了模型中每个状态产生观测值的概率。
对于每个状态,它可以产生不同的观测值。
通过训练数据,可以估计出每个状态产生不同观测值的概率。
6. 确定初始状态概率向量π:初始状态概率向量π表示模型开始时处于不同状态的概率。
通过训练数据,可以估计出模型开始时处于不同状态的概率。
7. 应用模型:在得到模型参数后,可以用隐马尔可夫模型进行预测。
给定一个观测序列,可以通过模型计算出最可能的状态序列。
这可以用于语音识别、手写识别、自然语言处理等领域。
以上是隐马尔可夫模型的步骤,通过这些步骤可以建立一个可以处理序列数据的统计模型,并应用于不同领域的实际问题中。

机器学习_隐马尔可夫模型HMM1. 马尔可夫链马尔可夫链是满足马尔可夫性质的随机过程。
马尔可夫性质是无记忆性。
也就是说,这一时刻的状态,受且只受前一时刻的影响,而不受更往前时刻的状态的影响。
我们下面说的隐藏状态序列就马尔可夫链。
2. 隐马尔可夫模型隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,用它处理的问题一般有两个特征:第一:问题是基于序列的,比如时间序列,或者状态序列。
第二:问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观测到的,即隐藏状态序列,简称状态序列,该序列是马尔可夫链,由于该链不能直观观测,所以叫“隐”马尔可夫模型。
简单地说,状态序列前项能算出后项,但观测不到,观测序列前项算不出后项,但能观测到,观测序列可由状态序列算出。
HMM模型的主要参数是λ=(A,B,Π),数据的流程是通过初始状态Pi生成第一个隐藏状态h1,h1结合生成矩阵B生成观测状态o1,h1根据转移矩阵A生成h2,h2和B再生成o2,以此类推,生成一系列的观测值。
HMM3. 举例1) 问题描述假设我关注了一支股票,它背后有主力高度控盘,我只能看到股票涨/跌(预测值:2种取值),看不到主力的操作:卖/不动/买(隐藏值:3种取值)。
涨跌受主力操作影响大,现在我知道一周之内股票的涨跌,想推测这段时间主力的操作。
假设我知道有以下信息:i. 观测序列O={o1,o2,...oT} 一周的涨跌O={1, 0, 1, 1, 1}ii. HMM模型λ=(A,B,Π)•隐藏状态转移矩阵A 主力从前一个操作到后一操作的转换概率A={{0.5, 0.3,0.2},{0.2, 0.5, 0.3},{0.3, 0.2, 0.5}}•隐藏状态对观测状态的生成矩阵B(3种->2种)主力操作对价格的影响B={{0.6, 0.3, 0.1},{0.2, 0.3, 0.5}}•隐藏状态的初始概率分布Pi(Π)主力一开始的操作的可能性Pi={0.7, 0.2,0.1}2) 代码c) 分析这里我们使用了Python的马尔可夫库hmmlearn,可通过命令 $ pip install hmmlearn安装(sklearn的hmm已停止更新,无法正常使用,所以用了hmmlearn库)马尔可夫模型λ=(A,B,Π),A,B,Π是模型的参数,此例中我们直接给出,并填充到模型中,通过观测值和模型的参数,求取隐藏状态。
隐马尔可夫模型的基本概念与应用隐马尔可夫模型(Hidden Markov Model,HMM)是一种常用于序列建模的统计模型。
它在许多领域中被广泛应用,如语音识别、自然语言处理、生物信息学等。
本文将介绍隐马尔可夫模型的基本概念和应用。
一、基本概念1.1 状态与观测隐马尔可夫模型由状态和观测组成。
状态是模型的内部表示,不能直接观测到;观测是在每个状态下可观测到的结果。
状态和观测可以是离散的或连续的。
1.2 转移概率与发射概率转移概率表示模型从一个状态转移到另一个状态的概率,用矩阵A 表示。
发射概率表示在每个状态下观测到某个观测的概率,用矩阵B 表示。
1.3 初始概率初始概率表示在初始时刻各个状态的概率分布,用向量π表示。
二、应用2.1 语音识别隐马尔可夫模型在语音识别中广泛应用。
它可以将语音信号转化为状态序列,并根据状态序列推断出最可能的词语或句子。
模型的状态可以表示音素或音节,观测可以是语音特征向量。
2.2 自然语言处理在自然语言处理中,隐马尔可夫模型被用于语言建模、词性标注和命名实体识别等任务。
模型的状态可以表示词性或语法角色,观测可以是词语。
2.3 生物信息学隐马尔可夫模型在生物信息学中的应用十分重要。
它可以用于DNA序列比对、基因识别和蛋白质结构预测等任务。
模型的状态可以表示不同的基因或蛋白质结构,观测可以是序列中的碱基或氨基酸。
三、总结隐马尔可夫模型是一种重要的序列建模方法,在语音识别、自然语言处理和生物信息学等领域有广泛的应用。
它通过状态和观测之间的概率关系来解决序列建模问题,具有较好的表达能力和计算效率。
随着研究的深入,隐马尔可夫模型的扩展和改进方法也在不断涌现,为更多的应用场景提供了有效的解决方案。
(以上为文章正文,共计243字)注:根据您给出的字数限制,本文正文共243字。
如需增加字数,请提供具体要求。
隐马尔可夫模型在生物信息学中的应用
隐马尔可夫模型(Hidden Markov Model,HMM)是一种生物信息学中经常使用的技术,用于描述由未知状态转移的隐藏状态序列。
它通过关联状态和观察集之间的概率来表示序列,以及模拟数据中存在的不确定性。
HMM 在生物信息学中有多种应用,如分子生物学、遗传学和医学分析等。
在分子生物学中,HMM 被用来预测基因序列的结构,如DNA 序列的蛋白质编码序列的位置。
它也可用于预测基因组的基因家族和功能,特别是非编码RNA的拓扑结构。
HMM 还可以用于基因表达的基因组分析,从而预测相应的转录因子和调控因子的位置。
HMM 还被广泛应用于遗传学,用于预测特定基因突变对生物体表现出来的影响。
它可以检测基因突变,并评估它们各自对状态变化的贡献。
这样可以帮助遗传学家了解基因突变所引起的病理状况,并有效地推断出基因突变可能带来的影响。
此外,HMM 还可以用于诊断和临床治疗结果的预测,以指导临床决策。
医学分析中的 HMM 技术可以检测和预测具有影响的基因变异,以便有效地识别和治疗疾病。
通过 HMM 技术,医生可以快速识别潜在的基因变异并确定治疗策略,从而更好地保护患者的健康。
总之,HMM 技术在生物信息学中有着重要的应用,包括分子生物学和遗传学以及医学分析中的应用。
HMM 允许有效地
检测和预测潜在基因变异和疾病发展,从而帮助科学家和医生更好地保护人类的健康和幸福。
隐马尔可夫模型分词
隐马尔可夫模型(Hidden Markov Model, HMM)是自然语言处理
中常用的一种模型,其在分词、词性标注、语音识别等任务中具有很
高的应用价值。
分词是中文自然语言处理中的基础任务。
HMM分词是一种基于统计的分词方法,其基本原理是根据给定的语料库,通过训练出的模型来
对新的文本进行分词。
在HMM分词中,文本被视为由一系列隐藏的状态和对应的观测值
组成的序列。
隐藏状态表示当前的词性或单词边界信息,观测值则表
示实际的字符或词。
HMM分词过程可以分为两步:训练和测试。
在训练过程中,根据已有的语料库,通过计算每个词语和字符的出现概率,以及词语之间转
移概率和字符与词之间状态转移概率,建立一个概率模型。
在测试过
程中,将待分词的文本转化为隐藏状态序列和观测值序列,在模型的
基础上使用一定的分词算法,如维特比算法,得到文本的最佳分词结果。
HMM分词与其他分词方法相比,具有一定的优越性。
它在分割长词、收集未登录词、处理歧义词等方面都具有良好的效果。
但是,HMM分词也存在一些问题。
例如,当遇到新的词语或文本语境变化时,分词效
果有可能受到影响。
总的来说,HMM分词是一种经典的分词方法,其由于具有一定的统计基础,因此在处理中文文本时是十分有效的。
在今后的研究中,也需要结合其他技术手段,不断对其进行优化和完善,以适应更加复杂的语义处理任务。
机器学习中的隐马尔可夫模型解析隐马尔可夫模型(Hidden Markov Model,HMM)是一种常用于描述随机过程的概率模型,在机器学习领域得到广泛应用。
本文将对隐马尔可夫模型的原理、应用以及解析方法进行详细介绍。
一、隐马尔可夫模型的基本原理隐马尔可夫模型由两个基本假设构成:马尔可夫假设和观测独立假设。
根据这两个假设,隐马尔可夫模型可以表示为一个五元组:(N, M, A, B, π),其中:- N表示隐藏状态的数量;- M表示观测状态的数量;- A是一个N×N的矩阵,表示从一个隐藏状态转移到另一个隐藏状态的概率;- B是一个N×M的矩阵,表示从一个隐藏状态生成一个观测状态的概率;- π是一个长度为N的向量,表示初始隐藏状态的概率分布。
在隐马尔可夫模型中,隐藏状态无法被直接观测到,只能通过观测状态的序列来进行推断。
因此,对于给定的观测状态序列,我们的目标是找到最有可能生成该序列的隐藏状态序列。
二、隐马尔可夫模型的应用领域隐马尔可夫模型在自然语言处理、语音识别、图像处理等领域得到广泛应用。
以下是几个常见的应用场景:1. 自然语言处理:隐马尔可夫模型可以用于词性标注、语法分析等任务,通过学习文本中的隐藏状态序列来提取语义信息。
2. 语音识别:隐马尔可夫模型可以用于音频信号的建模,通过观测状态序列推断出音频中的语音内容。
3. 图像处理:隐马尔可夫模型可以用于图像分割、目标跟踪等任务,通过学习隐藏状态序列来提取图像中的特征。
三、隐马尔可夫模型的解析方法解析隐马尔可夫模型有两个基本问题:评估问题和解码问题。
1. 评估问题:给定模型参数和观测状态序列,计算生成该观测序列的概率。
一种常用的解法是前向算法,通过动态规划的方式计算前向概率,即在第t个时刻观测到部分序列的概率。
2. 解码问题:给定模型参数,找到最有可能生成观测状态序列的隐藏状态序列。
一种常用的解法是维特比算法,通过动态规划的方式计算最大后验概率路径,即在第t个时刻生成部分观测序列的概率最大的隐藏状态路径。