隐马尔可夫模型_刘秉权
- 格式:pdf
- 大小:190.09 KB
- 文档页数:37


隐马尔可夫模型在语音识别中的应用隐马尔可夫模型(Hidden Markov Model,简称HMM)是一种强大的统计工具,主要用于序列数据的建模和分析。
语音是一种典型的序列数据,因此HMM在语音识别中有着广泛的应用。
本文将就HMM在语音识别中的各种应用进行详细介绍。
一、HMM模型HMM是一种统计模型,它可以描述一个由有限个状态(state)组成的随机过程(process),该过程的状态是非观测的,而只有通过一些不完全(incomplete)可观测的随机变量(observation)来观测该过程。
HMM模型由三个部分组成:状态集合、观测集合和参数集合。
其中,状态集合和观测集合是已知的,参数集合包括状态转移概率、发射概率和初始概率。
在语音识别中,HMM通常被用来表示语音的声学性质。
每个状态对应于一个语音音素(phoneme),而每个观测向量对应于一个声学特征向量。
通常使用高斯混合模型(GMM)来建模每个状态发射概率。
由于一个语音序列对应于一个状态序列和一个观测序列,因此可以通过基于HMM的Viterbi算法来计算最可能的状态序列,从而实现语音识别。
二、基于HMM的语音识别基于HMM的语音识别可以分为三个主要步骤:训练、解码和评估。
1. 训练训练是基于HMM的语音识别的重要步骤,它用于估计HMM模型的参数。
训练过程由两个部分组成:第一部分是初始化,第二部分是迭代优化。
初始化:初始化包括确定状态集合、观测集合和参数集合。
通常情况下,状态集合与待识别的音素集合相对应,而观测集合包括语音的声学特征向量。
初始参数一般采用随机初始化,或者通过聚类方法从数据中提取初始参数。
迭代优化:优化通常采用Baum-Welch算法(也称为EM算法),该算法用于最大化模型似然函数。
Baum-Welch算法是一种迭代算法,迭代过程中会反复运用E步骤和M步骤。
在E步骤中,HMM模型会被使用来计算当前状态概率分布。
在M步骤中,HMM模型会根据已知状态分布和观测数据来更新模型参数。


隐马尔科夫模型(Hidden Markov Model, HMM)是一种用于建模时序数据的统计模型,被广泛应用于语音识别、自然语言处理、生物信息学等领域。
在HMM中,系统状态是不可观测的,只能通过可观测的输出来推断系统状态。
本文将分析隐马尔科夫模型的训练技巧,包括参数估计、初始化、收敛性等方面。
数据预处理在进行HMM的训练之前,首先需要对输入数据进行预处理。
对于语音识别任务来说,预处理包括语音信号的特征提取,通常使用的特征包括梅尔频率倒谱系数(MFCC)、过零率等。
对于文本处理任务来说,预处理包括词袋模型、词嵌入等。
预处理的质量将直接影响HMM的训练效果,因此需要特别注意。
参数估计在HMM中,有三组参数需要估计:初始状态概率π、状态转移概率矩阵A和发射概率矩阵B。
其中,π表示系统在每个隐藏状态开始的概率,A表示系统从一个隐藏状态转移到另一个隐藏状态的概率,B表示系统从一个隐藏状态生成可观测输出的概率。
Baum-Welch算法是用于HMM参数估计的一种经典算法,它是一种迭代算法,通过不断更新参数的估计值,使得模型的似然函数逐步增大。
Baum-Welch算法的核心是前向-后向算法,它可以有效地估计HMM的参数,但是在实际应用中需要注意其对初始值的敏感性,容易陷入局部最优解。
模型初始化HMM的参数估计需要一个初始值,通常使用随机初始化的方法。
然而,随机初始化容易导致参数估计的不稳定,影响模型的训练效果。
因此,对HMM模型的初始化非常重要,可以使用专门的初始化方法,如K-means聚类算法、高斯混合模型等。
模型收敛性在进行HMM的训练过程中,需要考虑模型的收敛性。
HMM的收敛性通常通过设置迭代次数或者设定阈值来实现。
对于大规模数据集,可以考虑使用分布式计算或者并行计算的方法来加速模型的训练,以提高收敛性。
参数调优HMM模型的训练过程中,需要进行参数的调优。
参数调优可以通过交叉验证等方法来实现,以找到最优的参数组合。


⼀⽂搞懂HMM(隐马尔可夫模型)什么是熵(Entropy)简单来说,熵是表⽰物质系统状态的⼀种度量,⽤它⽼表征系统的⽆序程度。
熵越⼤,系统越⽆序,意味着系统结构和运动的不确定和⽆规则;反之,,熵越⼩,系统越有序,意味着具有确定和有规则的运动状态。
熵的中⽂意思是热量被温度除的商。
负熵是物质系统有序化,组织化,复杂化状态的⼀种度量。
熵最早来原于物理学. 德国物理学家鲁道夫·克劳修斯⾸次提出熵的概念,⽤来表⽰任何⼀种能量在空间中分布的均匀程度,能量分布得越均匀,熵就越⼤。
1. ⼀滴墨⽔滴在清⽔中,部成了⼀杯淡蓝⾊溶液2. 热⽔晾在空⽓中,热量会传到空⽓中,最后使得温度⼀致更多的⼀些⽣活中的例⼦:1. 熵⼒的⼀个例⼦是⽿机线,我们将⽿机线整理好放进⼝袋,下次再拿出来已经乱了。
让⽿机线乱掉的看不见的“⼒”就是熵⼒,⽿机线喜欢变成更混乱。
2. 熵⼒另⼀个具体的例⼦是弹性⼒。
⼀根弹簧的⼒,就是熵⼒。
胡克定律其实也是⼀种熵⼒的表现。
3. 万有引⼒也是熵⼒的⼀种(热烈讨论的话题)。
4. 浑⽔澄清[1]于是从微观看,熵就表现了这个系统所处状态的不确定性程度。
⾹农,描述⼀个信息系统的时候就借⽤了熵的概念,这⾥熵表⽰的是这个信息系统的平均信息量(平均不确定程度)。
最⼤熵模型我们在投资时常常讲不要把所有的鸡蛋放在⼀个篮⼦⾥,这样可以降低风险。
在信息处理中,这个原理同样适⽤。
在数学上,这个原理称为最⼤熵原理(the maximum entropy principle)。
让我们看⼀个拼⾳转汉字的简单的例⼦。
假如输⼊的拼⾳是"wang-xiao-bo",利⽤语⾔模型,根据有限的上下⽂(⽐如前两个词),我们能给出两个最常见的名字“王⼩波”和“王晓波 ”。
⾄于要唯⼀确定是哪个名字就难了,即使利⽤较长的上下⽂也做不到。
当然,我们知道如果通篇⽂章是介绍⽂学的,作家王⼩波的可能性就较⼤;⽽在讨论两岸关系时,台湾学者王晓波的可能性会较⼤。


隐马尔科夫模型在生物信息学中的应用隐马尔科夫模型(Hidden Markov Model, HMM)是一种用来描述状态序列的概率模型,在生物信息学中有着广泛的应用。
隐马尔科夫模型可以用来模拟DNA序列、蛋白质序列等生物数据,对于基因识别、蛋白质结构预测、序列比对等方面都有着重要的作用。
本文将从隐马尔科夫模型的基本原理、在生物信息学中的应用等方面进行论述。
一、隐马尔科夫模型的基本原理隐马尔科夫模型是一种包含隐含状态和可见状态的概率模型。
隐含状态是不可直接观测到的,而可见状态则是可以观测到的。
隐马尔科夫模型可以用一个三元组(A, B, π)来描述,其中A是状态转移概率矩阵,B是观测概率矩阵,π是初始状态概率分布。
通过这些参数,可以描述隐马尔科夫模型的状态转移和观测过程。
在生物信息学中,隐马尔科夫模型通常被用来对生物序列进行建模。
例如,在基因识别中,DNA序列中的基因区域和非基因区域可以被看作是隐含状态和可见状态,通过训练隐马尔科夫模型,可以对基因区域和非基因区域进行区分。
二、隐马尔科夫模型在基因识别中的应用基因识别是生物信息学中的重要问题之一。
隐马尔科夫模型在基因识别中的应用得到了广泛的关注和研究。
通过在训练集上对隐马尔科夫模型进行训练,可以得到基因区域和非基因区域的状态转移概率和观测概率。
然后,利用这些参数,可以对新的DNA序列进行基因识别。
隐马尔科夫模型在基因识别中的应用不仅可以提高基因识别的准确率,还可以帮助研究人员发现新的基因。
这对于深入理解生物基因的功能和进化具有重要意义。
三、隐马尔科夫模型在蛋白质结构预测中的应用蛋白质结构预测是生物信息学中的另一个重要问题。
隐马尔科夫模型在蛋白质结构预测中的应用也取得了一些成果。
通过对蛋白质序列的结构特征进行建模,可以利用隐马尔科夫模型进行蛋白质结构的预测。
隐马尔科夫模型在蛋白质结构预测中的应用可以帮助研究人员理解蛋白质的结构与功能之间的关系,对于设计新的药物分子和研究蛋白质的功能具有重要意义。
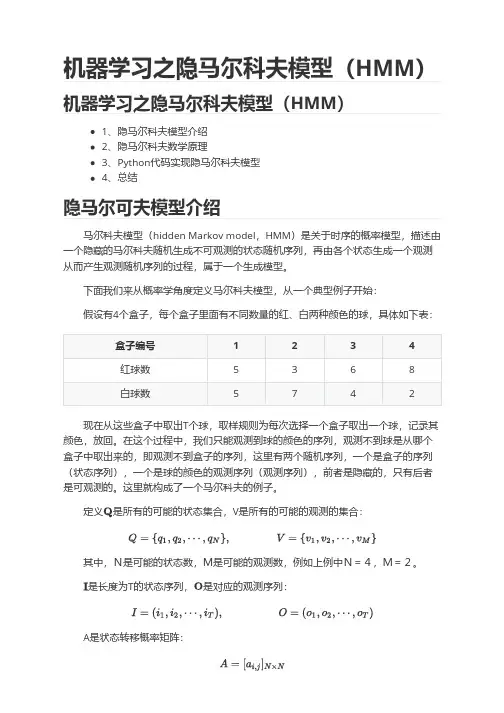
机器学习之隐马尔科夫模型(HMM)机器学习之隐马尔科夫模型(HMM)1、隐马尔科夫模型介绍2、隐马尔科夫数学原理3、Python代码实现隐马尔科夫模型4、总结隐马尔可夫模型介绍马尔科夫模型(hidden Markov model,HMM)是关于时序的概率模型,描述由一个隐藏的马尔科夫随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程,属于一个生成模型。
下面我们来从概率学角度定义马尔科夫模型,从一个典型例子开始:假设有4个盒子,每个盒子里面有不同数量的红、白两种颜色的球,具体如下表:盒子编号1234红球数5368白球数5742现在从这些盒子中取出T个球,取样规则为每次选择一个盒子取出一个球,记录其颜色,放回。
在这个过程中,我们只能观测到球的颜色的序列,观测不到球是从哪个盒子中取出来的,即观测不到盒子的序列,这里有两个随机序列,一个是盒子的序列(状态序列),一个是球的颜色的观测序列(观测序列),前者是隐藏的,只有后者是可观测的。
这里就构成了一个马尔科夫的例子。
定义是所有的可能的状态集合,V是所有的可能的观测的集合:其中,N是可能的状态数,M是可能的观测数,例如上例中N=4,M=2。
是长度为T的状态序列,是对应的观测序列:A是状态转移概率矩阵:其中, 是指在时刻处于状态的条件下在时刻转移到状态的概率。
B是观测概率矩阵:其中, 是指在时刻处于状态的条件下生成观测的概率。
是初始状态概率向量:其中, 是指在时刻=1处于状态的概率。
由此可得到,隐马尔可夫模型的三元符号表示,即称为隐马尔可夫模型的三要素。
由定义可知隐马尔可夫模型做了两个基本假设:(1)齐次马尔科夫性假设,即假设隐藏的马尔科夫链在任意时刻的状态只和-1状态有关;(2)观测独立性假设,观测只和当前时刻状态有关;仍以上面的盒子取球为例,假设我们定义盒子和球模型:状态集合: = {盒子1,盒子2,盒子3,盒子4}, N=4观测集合: = {红球,白球} M=2初始化概率分布:状态转移矩阵:观测矩阵:(1)转移概率的估计:假设样本中时刻t处于状态i,时刻t+1转移到状态j 的频数为那么转台转移概率的估计是:(2)观测概率的估计:设样本中状态为j并观测为k的频数是那么状态j观测为k的概率, (3)初始状态概率的估计为S个样本中初始状态为的频率。


隐马尔科夫模型(HMM)在生物信息学中的应用引言生物信息学是一门跨学科的学科,它将生物学和计算机科学相结合,以研究生物信息的获取、存储、分析和应用。
隐马尔科夫模型(HMM)作为一种概率模型,在生物信息学中得到了广泛的应用。
本文将探讨HMM在生物信息学中的应用,包括蛋白质结构预测、基因识别、DNA序列比对以及其他方面的应用。
HMM在蛋白质结构预测中的应用蛋白质是生物体内的重要分子,其结构对其功能起着至关重要的作用。
利用HMM可以对蛋白质结构进行预测。
HMM可以将蛋白质的氨基酸序列映射到其结构空间中,从而帮助科学家们预测出蛋白质的三维结构。
这对于研究蛋白质的功能、相互作用等方面具有重要意义。
HMM在基因识别中的应用基因是生物体遗传信息的载体,基因识别是生物信息学中的一个重要问题。
HMM可以帮助科学家们识别出基因组中的基因。
利用HMM对DNA序列进行建模,可以有效地识别出其中的编码区域和非编码区域,从而帮助科学家们理解基因的功能和结构。
HMM在DNA序列比对中的应用DNA序列比对是生物信息学中的另一个重要问题,它可以帮助科学家们研究不同物种之间的亲缘关系、寻找共同的基因等。
HMM可以用于DNA序列的比对,通过建立模型来发现序列之间的相似性和差异性。
这对于研究物种的进化、基因的保守性等方面具有重要意义。
HMM在其他生物信息学问题中的应用除了以上几个方面,HMM还在生物信息学中的其他问题中得到了广泛的应用。
比如在蛋白质家族的分类、蛋白质结构域的识别、RNA序列的结构预测等方面,HMM都发挥着重要的作用。
HMM作为一种灵活且强大的概率模型,可以对各种类型的生物信息进行建模和分析。
结论隐马尔科夫模型在生物信息学中发挥着重要的作用,它帮助科学家们解决了许多生物信息学中的重要问题,包括蛋白质结构预测、基因识别、DNA序列比对以及其他方面的应用。
随着生物信息学的发展和技术的不断进步,HMM在生物信息学中的应用将会越来越广泛,为我们深入理解生物学和生命科学提供更多的可能。
马尔科夫过程马尔科夫过程可以看做是一个自动机,以一定的概率在各个状态之间跳转。
考虑一个系统,在每个时刻都可能处于N个状态中的一个,N个状态集合是{S1,S2,S3,...S N}。
我们如今用q1,q2,q3,…q n来表示系统在t=1,2,3,…n时刻下的状态。
在t=1时,系统所在的状态q取决于一个初始概率分布PI,PI(S N)表示t=1时系统状态为S N的概率。
马尔科夫模型有两个假设:1. 系统在时刻t的状态只与时刻t-1处的状态相关;〔也称为无后效性〕2. 状态转移概率与时间无关;〔也称为齐次性或时齐性〕第一条详细可以用如下公式表示:P(q t=S j|q t-1=S i,q t-2=S k,…)= P(q t=S j|q t-1=S i)其中,t为大于1的任意数值,S k为任意状态第二个假设那么可以用如下公式表示:P(q t=S j|q t-1=S i)= P(q k=S j|q k-1=S i)其中,k为任意时刻。
下列图是一个马尔科夫过程的样例图:可以把状态转移概率用矩阵A表示,矩阵的行列长度均为状态数目,a ij表示P(S i|S i-1)。
隐马尔科夫过程与马尔科夫相比,隐马尔科夫模型那么是双重随机过程,不仅状态转移之间是个随机事件,状态和输出之间也是一个随机过程,如下列图所示:此图是从别处找来的,可能符号与我之前描绘马尔科夫时不同,相信大家也能理解。
该图分为上下两行,上面那行就是一个马尔科夫转移过程,下面这一行那么是输出,即我们可以观察到的值,如今,我们将上面那行的马尔科夫转移过程中的状态称为隐藏状态,下面的观察到的值称为观察状态,观察状态的集合表示为O={O1,O2,O3,…O M}。
相应的,隐马尔科夫也比马尔科夫多了一个假设,即输出仅与当前状态有关,可以用如下公式表示:P(O1,O2,…,O t|S1,S2,…,S t)=P(O1|S1)*P(O2|S2)*...*P(O t|S t) 其中,O1,O2,…,O t为从时刻1到时刻t的观测状态序列,S1,S2,…,S t那么为隐藏状态序列。
隐马尔可夫模型(HMM)是一种用于对时序数据进行建模和分析的概率模型,特别适用于具有一定的隐含结构和状态转移概率的数据。
在自然语言处理、语音识别、生物信息学等领域中,HMM都有着广泛的应用。
在本文中,我将向您介绍HMM的基本概念和原理,并共享如何使用Matlab来实现HMM模型。
1. HMM基本概念和原理隐马尔可夫模型是由隐含状态和可见观测两部分组成的,其中隐含状态是不可见的,而可见观测是可以被观测到的。
在HMM中,隐含状态和可见观测之间存在转移概率和发射概率。
通过这些概率,HMM可以描述一个系统在不同隐含状态下观测到不同可见观测的概率分布。
HMM可以用状态转移矩阵A和发射矩阵B来表示,同时也需要一个初始状态分布π来描述系统的初始状态。
2. Matlab实现HMM模型在Matlab中,我们可以使用HMM工具箱(HMM Toolbox)来实现隐马尔可夫模型。
我们需要定义系统的隐含状态数目、可见观测的数目以及状态转移概率矩阵A和发射概率矩阵B。
利用Matlab提供的函数,可以方便地计算出系统在给定观测下的概率分布,以及通过学习的方法来调整参数以适应实际数据。
3. 在Matlab中实现HMM模型需要注意的问题在实现HMM模型时,需要注意参数的初始化和调整,以及对于不同类型的数据如何选择合适的模型和算法。
在使用HMM模型对实际问题进行建模时,需要考虑到过拟合和欠拟合等问题,以及如何有效地利用HMM模型进行预测和决策。
总结通过本文的介绍,我们可以了解到隐马尔可夫模型在时序数据建模中的重要性,以及如何使用Matlab来实现HMM模型。
对于HMM的进一步学习和实践,我个人认为需要多实践、多探索,并结合具体应用场景来深入理解HMM模型的原理和方法。
在今后的学习和工作中,我相信掌握HMM模型的实现和应用将对我具有重要的帮助。
我会继续深入学习HMM模型,并将其运用到实际问题中,以提升自己的能力和水平。
以上是我对隐马尔可夫模型的个人理解和观点,希望对您有所帮助。
隐马尔可夫模型(HMM)是一种统计模型,常用于语音识别、自然语言处理等领域。
它主要用来描述隐藏的马尔可夫链,即一种具有未知状态的马尔可夫链。
在语音识别中,HMM被广泛应用于对语音信号进行建模和识别。
下面我将从HMM的基本概念、参数迭代和语音识别应用等方面展开阐述。
1. HMM的基本概念在隐马尔可夫模型中,有三种基本要素:状态、观测值和状态转移概率及观测概率。
状态表示未知的系统状态,它是隐藏的,无法直接观测到。
观测值则是我们可以观测到的数据,比如语音信号中的频谱特征等。
状态转移概率描述了在不同状态之间转移的概率,而观测概率则表示在每个状态下观测到不同观测值的概率分布。
2. HMM参数迭代HMM的参数包括初始状态概率、状态转移概率和观测概率。
在实际应用中,这些参数通常是未知的,需要通过观测数据进行估计。
参数迭代是指通过一定的算法不断更新参数的过程,以使模型更好地拟合观测数据。
常见的参数迭代算法包括Baum-Welch算法和Viterbi算法。
其中,Baum-Welch算法通过最大化似然函数来估计模型的参数,Viterbi算法则用于解码和预测。
3. HMM在语音识别中的应用在语音识别中,HMM被广泛用于建模和识别语音信号。
语音信号被转换成一系列的特征向量,比如MFCC(Mel-Frequency Cepstral Coefficients)特征。
这些特征向量被用来训练HMM模型,学习模型的参数。
在识别阶段,通过Viterbi算法对输入语音进行解码,得到最可能的文本输出。
4. 个人观点和理解从个人角度看,HMM作为一种强大的统计模型,在语音识别领域有着重要的应用。
通过不断迭代参数,HMM能够更好地建模语音信号,提高语音识别的准确性和鲁棒性。
然而,HMM也面临着状态空间爆炸、参数收敛速度慢等问题,需要结合其他模型和算法进行改进和优化。
总结回顾通过本文对隐马尔可夫模型(HMM)的介绍,我们从基本概念、参数迭代和语音识别应用等方面对HMM有了更深入的了解。
隐马尔科夫模型(Hidden Markov Model,HMM)是一种在语音识别中得到广泛应用的统计模型。
它的应用为语音识别技术的发展提供了重要的基础,同时也在人工智能领域起到了重要的作用。
首先,我们来了解一下HMM的基本原理。
HMM是一种用来描述一系列观测数据序列的概率模型。
它的核心思想是假设观测数据序列背后存在一个隐含的状态序列,而观测数据的生成过程是由这个隐含状态序列控制的。
在语音识别中,HMM可以用来建模一个人说话时发出的声音信号序列。
声音信号的特征可以被看作是观测数据,而人说话时所处的发音状态可以被看作是隐含的状态序列。
通过观测数据序列来推断出隐含状态序列,就可以实现对语音信号的识别。
HMM在语音识别中的应用有多个关键环节。
首先是声学建模,即对语音信号的特征进行建模。
在HMM中,通常会使用高斯混合模型(Gaussian Mixture Model,GMM)来描述不同发音状态的概率分布。
每个发音状态都可以用一个GMM来表示,而HMM则可以将这些发音状态连接起来,形成一个完整的语音模型。
这样一来,当一个声音信号输入时,HMM可以根据观测数据来推断出最有可能的发音状态序列,从而实现对语音信号的识别。
另一个关键环节是语言建模,即对语音信号的语言特征进行建模。
在语音识别中,通常会使用n-gram模型来对语言特征进行建模。
这样一来,HMM可以综合考虑声学特征和语言特征,从而提高语音识别的准确性。
除了声学建模和语言建模,HMM还可以在识别和解码阶段进行Viterbi算法来寻找最可能的词序列。
这一算法可以有效地解决HMM所带来的多义性和多解性问题,从而提高了语音识别的准确性和鲁棒性。
总的来说,HMM在语音识别中的应用可以帮助人们更准确地理解和识别语音信号,从而提高了人机交互的效率。
随着人工智能技术的不断发展,HMM在语音识别领域的应用也将不断得到拓展和完善,为人们的日常生活和工作带来更多便利和可能性。