高中数学完整讲义指数与指数函数1指数基本运算

高一指数运算知识点归纳指数运算是数学中一个重要的概念，它在高中数学中占据着重要的地位。

在高一阶段学习中，我们需要掌握指数运算的基本知识和技巧，以便能够灵活运用于各种实际问题。

本文将对高一指数运算的知识点进行归纳总结，以便同学们系统地复习和掌握。

一、指数的基本定义和性质指数是数字在乘方运算中的角色，它用于表示底数被乘的次数。

指数运算具有以下基本定义和性质：1. 指数的定义：若a和n为实数，n为正整数，则a的n次方运算定义为a^n=a*a*a*...*a（共有n个a相乘）。

2. 幂运算的性质：a) 同底数相乘，指数相加：a^m * a^n = a^(m+n)；b) 同底数相除，指数相减：a^m / a^n = a^(m-n)；c) 乘方的乘方，指数相乘：(a^m)^n = a^(m*n)；d) 乘方的分配律：a^m * b^m = (a * b)^m。

二、指数的运算规则在指数运算中，我们需要掌握如下几个重要的运算规则：1. 同底数幂相乘：a^m * a^n = a^(m+n)。

这条规则表明，在指数幂相乘时，只需保持底数不变，指数相加即可。

2. 同底数幂相除：a^m / a^n = a^(m-n)。

这条规则表明，在指数幂相除时，只需保持底数不变，指数相减即可。

3. 幂的乘方：(a^m)^n = a^(m*n)。

这条规则表明，在幂的乘方运算中，先求得幂内的乘方结果，然后将指数相乘。

4. 零次幂规定：a^0 = 1。

这条规定表明，任何非零数的0次方都等于1。

5. 负指数的规定：a^(-n) = 1 / a^n。

这条规定表明，一个数的负指数幂等于这个数的倒数的正指数幂。

6. 科学计数法：对于形如a * 10^b的科学计数法，可以将其转化为指数形式：a * 10^b = m * 10^n，其中1 ≤ m < 10，且满足a =m * 10^(b-n)。

三、指数的特殊运算在指数运算中，有几个特殊的形式需要注意和灵活应用：1. 平方数和立方数：a^2表示a的平方，a^3表示a的立方。

指数函数讲义经典整理（含答案）一、同步知识梳理知识点1：指数函数函数(01)xy a a a =>≠且叫做指数函数，其中x 是自变量，函数的定义域是R知识点2：指数函数的图像和性质知识点3：指数函数的底数与图像的关系指数函数在同一直角坐标系中的图像的相对位置与底数大小的关系 如图所示，则01c d a b <<<<<，在y 轴右侧，图像从下到上相应的底数也由小变大， 在y 轴左侧，图像从上到下相应的底数也由小变大 即无论在y 轴左侧还是右侧，底数按逆时针方向变大在第一象限内，“底大图高”知识点4：指数式、指数函数的理解① 分数指数幂与根式或以互化，通常利用分数指数幂进行根式的运算② 根式的运算、变形、求值、化简及等式证明在数学中占有重要的地位，是研究方程、不等式和函数的基础，应引起重视③ 在有关根式、分数指数幂的变形、求值过程中，要注意运用方程的观点处理问题，通过解方程或方程组来求值④ 在理解指数函数的概念时，应抓住定义的“形式”，像1223,,21xx y y x y y =⋅===- 等函数均不符合形式()01x y a a a =>≠且，因此，它们都不是指数函数⑤ 画指数函数x y a =的图像，应抓住三个关键点：()()11,,0,1,1,a a ⎛⎫- ⎪⎝⎭二、同步题型分析题型1：指数函数的定义、解析式、定义域和值域例1：已知函数，且． （1）求m 的值；（2）判定f （x ）的奇偶性；（3）判断f （x ）在（0，+∞）上的单调性，并给予证明．考点：指数函数的定义、解析式、定义域和值域；函数单调性的判断与证明． 专题： 计算题． 分析：（1）欲求m 的值，只须根据f （4）=的值，当x=4时代入f （x ）解一个指数方程即可；（2）求出函数的定义域x|x≠0}，利用奇偶性的定义判断f （x ）与f （﹣x ）的关系，即可得到答案； （3）利用单调性的定义证明即可．任取0＜x1＜x2，只要证明f （x1）＞f （x2），即可． 解答： 解：（1）因为，所以，所以m=1．（2）因为f （x ）的定义域为{x|x≠0}，又，所以f （x ）是奇函数． （3）任取x1＞x2＞0，则，因为x1＞x2＞0，所以，所以f （x1）＞f （x2），所以f（x）在（0，+∞）上为单调增函数．点评：本题主要考查了函数单调性的判断、函数奇偶性的判断，与证明及指数方程的解法．在判定函数奇偶性时，一定注意函数的定义域关于原点对称，属于基础题．例2：已知函数，（1）讨论函数的奇偶性；（2）证明：f（x）＞0．考点：指数函数的定义、解析式、定义域和值域；函数奇偶性的判断；函数奇偶性的性质．专题：计算题．分析：（1）由2x﹣1≠0解得义域为{x|x≠0}，关于原点对称．f（﹣x）=（）（﹣x）=（）x=f（x），故该函数为偶函数．（2）任取x∈{x|x≠0}，当x＞0时，2x＞20=1且x＞0，故，从而．当x＜0时，﹣x＞0，故f（﹣x）＞0，由函数为偶函数，能证明f（x）＞0在定义域上恒成立．解答：解：（1）该函数为偶函数．由2x﹣1≠0解得x≠0即义域为{x|x≠0}关于原点对称…（2分）f（﹣x）=（）（﹣x）=﹣（+）x=（）x=（）x=（）x=f（x）（6分）故该函数为偶函数．…（7分）（2）证明：任取x∈{x|x≠0}当x＞0时，2x＞20=1且x＞0，∴2x﹣1＞0，故从而…（11分）当x＜0时，﹣x＞0，∴f（﹣x）＞0，…（12分）又因为函数为偶函数，∴f（x）=f（﹣x）＞0，…（13分）∴f（x）＞0在定义域上恒成立．…（14分）点评：本题考查函数的奇偶性的判断和证明f（x）＞0．解题时要认真审题，注意指数函数性质的灵活运用．例3：已知函数y=ax（a＞0且a≠1）在[1，2]上的最大值与最小值之和为20，记．（1）求a的值；（2）求f（x）+f（1﹣x）的值；（3）求的值．考点：指数函数的定义、解析式、定义域和值域．专题：综合题；函数的性质及应用．分析：（1）由y=ax单调得a+a2=20，由此可求a；（2）写出f（x），代入运算可得；（3）借助（2）问结论分n为奇数、偶数讨论可求；解答：解：（1）∵函数y=ax（a＞0且a≠1）在[1，2]上的最大值与最小值之和为20，且y=ax单调，∴a+a2=20，得a=4，或a=﹣5（舍去）；（2）由（1）知，∴====1；（3）由（2）知f（x）+f（1﹣x）=1，得n为奇数时，=×1=；n为偶数时，=+f（）==；综上，=．点评：本题考查指数函数的单调性、最值等知识，属中档题．题型2：指数函数的图像变换．例1：已知函数y=|2x﹣2|（1）作出其图象；（2）由图象指出函数的单调区间；（3）由图象指出当x取何值时，函数有最值，并求出最值．考点：指数函数的图像变换．专题：综合题；函数的性质及应用．分析：（1）函数y=|2x﹣2|图象是由y=2x的图象向下平移2个单位，再将x轴下方的部分翻着到x轴上方得到．（2）结合函数的图象，可得函数的减区间和增区间．（3）数形结合可得，当x=1时，ymiin=0．解答：解：（1）函数y=|2x﹣2|图象是由y=2x的图象向下平移2个单位，再将x轴下方的部分翻着到x轴上方得到，如图所示：（2）结合函数的图象，可得函数的减区间为（﹣∞，1]，增区间为（1，+∞）．（3）数形结合可得，当x=1时，ymiin=0．点评：本题主要考查指数函数的图象和性质综合，体现了数形结合的数学思想，属于中档题．题型3：指数函数单调性例1：已知函数f（x）=a•2x+b•3x，其中常数a，b满足a•b≠0（1）若a•b＞0，判断函数f（x）的单调性；（2）若a=﹣3b，求f（x+1）＞f（x）时的x的取值范围．考点：指数函数的单调性与特殊点；函数单调性的判断与证明；函数单调性的性质．专题：函数的性质及应用．分析：（1）分a＞0，b＞0和a＜0，b＜0两种情况讨论，运用单调性的定义可作出判断；（2）当a=﹣3b时，f（x）=﹣3b•2x+b•3x=b（3x﹣3•2x），分b＞0，b＜0两种情况进行讨论，整理可得指数不等式解出即可；解答：解：（1）当a＞0，b＞0时，任意x1，x2∈R，且x1＜x2，则f（x1）﹣f（x2）=a（﹣）+b（﹣），∵＜，＜，a＞0，b＞0，∴a（﹣）＜0，b（﹣）＜0，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），故函数f（x）在R上是增函数；当a＜0，b＜0时，同理，可判断函数f（x）在R上是减函数；（2）当a=﹣3b时，f（x）=﹣3b•2x+b•3x=b（3x﹣3•2x），则f（x+1）＞f（x）即化为b（3x+1﹣3•2x+1）＞b（3x﹣3•2x），若b＞0，则有3x+1﹣3•2x+1＞3x﹣3•2x，整理得，解得x＞1；若b＜0，则有3x+1﹣3•2x+1＜3x﹣3•2x，整理得，解得x＜1；故b＞0时，x的范围是x＞1；当b＜0时，x的范围是x＜1．点评：本题考查函数单调性的判断、指数函数的单调性的应用，考查分类讨论思想，属基础题．例2：已知定义在（﹣1，1）上的奇函数f（x）．在x∈（﹣1，0）时，f（x）=2x+2﹣x．（1）试求f（x）的表达式；（2）用定义证明f（x）在（﹣1，0）上是减函数；（3）若对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立，求实数t的取值范围．考点：指数函数综合题；奇偶性与单调性的综合．专题：计算题；函数的性质及应用．分析：（1）由f（x）是定义在（﹣1，1）上的奇函数可得f（0）=0，x∈（0，1）时，f（x）=﹣f（﹣x）=﹣（2x+2﹣x）；从而写出f（x）的表达式；（2）取值，作差，化简，判号，下结论五步；（3）对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立转化为对于x∈（0，1）上的每一个值，不等式t＞﹣恒成立，从而可得．解答：解：（1）∵f（x）是定义在（﹣1，1）上的奇函数，∴f（0）=0，设∈（0，1），则﹣x∈（﹣1，0），则f（x）=﹣f（﹣x）=﹣（2x+2﹣x），故f（x）=；（2）任取x1，x2∈（﹣1，0），且x1＜x2，则f（x1）﹣f（x2）=+﹣（+）=，∵x1＜x2＜0，∴﹣＜0，0＜＜1，故f（x1）﹣f（x2）＞0，故f（x）在（﹣1，0）上是减函数；（3）由题意，t•2x•f（x）＜4x﹣1可化为t•2x•（﹣（2x+2﹣x））＜4x﹣1，化简可得，t＞﹣，令g（x）=﹣=﹣1+，∵x∈（0，1），∴g（x）＜﹣1+=0，故对于x∈（0，1）上的每一个值，不等式t•2x•f（x）＜4x﹣1恒成立可化为t≥0．点评：本题考查了函数的性质的综合应用及恒成立问题的处理方法，属于难题．例3：已知函数f（x）=|2x﹣1﹣1|，（x∈R）．（1）证明：函数f（x）在区间（1，+∞）上为增函数，并指出函数f（x）在区间（﹣∞，1）上的单调性；（2）若函数f（x）的图象与直线y=t有两个不同的交点A（m，t），B（n，t），其中m＜n，求m+n 的取值范围．考点：指数函数综合题．专题：计算题；证明题．分析：（1）函数单调性的证明，通常依据定义，步骤为：取值，作差，变形，定号，下结论，由于与指数函数有关，求解时要利用到指数函数的单调性；（2）由（1）可知，函数的值域为（0，1），要使函数f（x）的图象与直线y=t有两个不同的交点，故有t∈（0，1）又函数f（x）的图象与直线y=t有两个不同的交点，所以A（m，t），B（n，t）分别位于直线x=1的两侧，由m＜n，得m＜1＜n，故可以求出m+n，进而由t∈（0，1），可求m+n的取值范围．解答：解：（1）证明：任取x1∈（1，+∞），x2∈（1，+∞），且x1＜x2，=，∵x1＜x2，∴，∴，∴f（x1）＜f（x2）．所以f（x）在区间（1，+∞）上为增函数．（5分）函数f（x）在区间（﹣∞，1）上为减函数．（6分）（2）因为函数f（x）在区间（1，+∞）上为增函数，相应的函数值为（0，+∞），在区间（﹣∞，1）上为减函数，相应的函数值为（0，1），由题意函数f（x）的图象与直线y=t有两个不同的交点，故有t∈（0，1），（8分）易知A（m，t），B（n，t）分别位于直线x=1的两侧，由m＜n，得m＜1＜n，故2m﹣1﹣1＜0，2n ﹣1﹣1＞0，又A，B两点的坐标满足方程t=|2x﹣1﹣1|，故得t=1﹣2m﹣1，t=2n﹣1﹣1，即m=log2（2﹣2t），n=log2（2+2t），（12分）故m+n=log2（2﹣2t）+log2（2+2t）=log2（4﹣4t2），当0＜t＜1时，0＜4﹣4t2＜4，﹣∞＜log2（4﹣4t2）＜2．因此，m+n的取值范围为（﹣∞，2）．（17分）点评：本题的考点是指数函数综合问题，主要考查函数单调性的证明，考查函数图形的性质，有较强的综合性．依据定义，证明函数的单调性的步骤通常为：取值，作差，变形，定号，下结论三、课堂达标检测检测题1：已知函数f（x）=（其中e=2.71828…是一个无理数）．（1）求函数f（x）的定义域；（2）判断奇偶性并证明之；（3）判断单调性并证明之．考点：指数函数的定义、解析式、定义域和值域；函数单调性的判断与证明；函数奇偶性的判断．专题：计算题；证明题．分析：（1）把分子整理变化成和分母相同的一部分，进行分子常数化，则变量只在分母上出现，根据分母是一个指数形式，恒大于零，得到函数的定义域是全体实数．（2）根据上一问值函数的定义域关于原点对称，从f（﹣x）入手整理，把负指数变化为正指数，就得到结果，判断函数是一个奇函数．（3）根据判断函数单调性的定义，设出两个任意的自变量，把两个自变量的函数值做差，化成分子和分母都是因式乘积的形式，根据指数函数的性质，判断差和零的关系．解答：解：f（x）==1﹣（1）∵e2x+1恒大于零，∴x∈R（2）函数是奇函数∵f（﹣x）==又由上一问知函数的定义域关于原点对称，∴f（x）为奇函数（3）是一个单调递增函数设x1，x2∈R 且x1＜x2则f（x1）﹣f（x2）=1﹣=∵x1＜x2，∴∴f（x1）﹣f（x2）＜0即f（x1）＜f（x2）∴f（x）在R是单调增函数点评：本题考查函数的定义域，考查函数的奇偶性的判断及证明．考查函数单调性的判断及证明，考查解决问题的能力，是一个综合题目．检测题2：已知函数f（x）=2ax+2（a为常数）（1）求函数f（x）的定义域．（2）若a=1，x∈（1，2]，求函数f（x）的值域．（3）若f（x）为减函数，求实数a的取值范围．考点：指数函数的定义、解析式、定义域和值域；指数函数的单调性与特殊点．专题：常规题型；转化思想．分析：（1）利用指数函数的定义域来考虑．（2）利用函数f（x）在（1，2]上的单调性求函数的值域．（3）根据复合函数的单调性，函数u=ax+2必须为减函数．解答：解：（1）函数y=2ax+2对任意实数都有意义，所以定义域为实数集R．（2）因为a=1，所以f（x）=2x+2．易知此时f（x）为增函数．又因为1＜x≤2，所以f（1）＜f（x）≤f（2），即8＜f（x）≤16．所以函数f（x）的值域为（8，16]．（3）因为f（x）为减函数，而y=2u是增函数，所以函数u=ax+2必须为减函数．所以得a＜0点评：本题考查指数函数的定义域、值域、单调性，复合函数的单调性，体现转化的数学思想．检测题3：设f（x）的定义域是（﹣∞，0）∪（0，+∞），且f（x）对任意不为零的实数x都满足f（﹣x）=﹣f（x）．已知当x＞0时（1）求当x＜0时，f（x）的解析式（2）解不等式．考点：指数函数的定义、解析式、定义域和值域；函数奇偶性的性质．专题：常规题型．分析：（1）求当x＜0时，f（x）的解析式，在哪个区间上求解析式，就在哪个区间上取值x，再转化到已知区间上求解析式，由f（﹣x）=﹣f（x）解出f（x）即可．（2）解不等式f（x）＜﹣，分x＞0和x＜0两种情况，根据求得的解析式求解即可．解答：解：（1）当x＜0时，﹣x＞0，=又f（﹣x）=﹣f（x）所以，当x＜0时，（2）x＞0时，，∴化简得∴，解得1＜2x＜4∴0＜x＜2当x＜0时，∴解得2x＞1（舍去）或∴x＜﹣2解集为{x|x＜﹣2或0＜x＜2}点评：本题考查分段函数解析式的求法，注意在哪个区间上求解析式，就在哪个区间上取值，再转化到已知的区间上求解析式，再根据奇偶性，解出f（x）来．解不等式也要分段求解，注意x的取值范围．11。

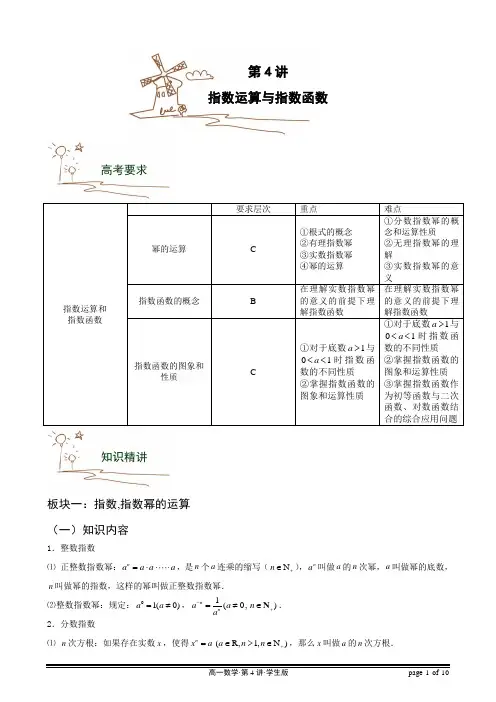
指数运算和 指数函数要求层次重点 难点幂的运算 C①根式的概念 ②有理指数幂 ③实数指数幂 ④幂的运算 ①分数指数幂的概念和运算性质②无理指数幂的理解③实数指数幂的意义指数函数的概念 B在理解实数指数幂的意义的前提下理解指数函数在理解实数指数幂的意义的前提下理解指数函数指数函数的图象和性质C①对于底数1a >与01a <<时指数函数的不同性质 ②掌握指数函数的图象和运算性质①对于底数1a >与01a <<时指数函数的不同性质 ②掌握指数函数的图象和运算性质 ③掌握指数函数作为初等函数与二次函数、对数函数结合的综合应用问题板块一：指数,指数幂的运算 （一）知识内容1．整数指数⑴ 正整数指数幂：n a a a a =⋅⋅⋅，是n 个a 连乘的缩写（N n +∈），n a 叫做a 的n 次幂，a 叫做幂的底数，n 叫做幂的指数，这样的幂叫做正整数指数幂．⑵整数指数幂：规定：01(0)a a =≠，1(0,)n n a a n a-+=≠∈N ． 2．分数指数⑴ n 次方根：如果存在实数x ，使得n x a =(R,1,N )a n n +∈>∈，那么x 叫做a 的n 次方根．高考要求第4讲指数运算与指数函数知识精讲⑵ 求a 的n 次方根，叫做a 开n 次方，称做开方运算．① 当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数．这时，a 的n表示．② 当n 是偶数时，正数的n 次方根有两个，它们互为相反数．正数a 的正、负n0)a >．⑶正数a 的正n 次方根叫做a 的n 次算术根．负数没有偶次方根．0的任何次方根都是00．n 叫做根指数，a3．根式恒等式：n a =；当na =；当n||a a a ⎧=⎨-⎩0a a <≥．4．分数指数幂的运算法则⑴正分数指数幂可定义为：1(0)na a >0,,,)mm nma a n m n+==>∈N 且为既约分数 ⑵负分数指数幂可定义为：1(0,,,)m nm nmaa n m na-+=>∈N 且为既约分数 5．整数指数幂推广到有理指数幂的运算性质： ⑴(0,,Q)r s r s a a a a r s +=>∈ ⑵()(0,,Q)r s rs a a a r s =>∈ ⑶()(0,0,Q)r r r ab a b a b r =>>∈6．n 次方根的定义及性质：n 为奇数时a =，n 为偶数时a =． 7．m na =m na-=（0a >，,*m n N ∈，且1n >）零的正分数指数幂为0，0的负分数指数幂没有意义．8．指数的运算性质：r s r s a a a +=，()rr r ab a b =（其中,0a b >，,r s ∈R ）9．无理数指数幂⑴ 无理指数幂(0,a a αα>是无理数）是一个确定的实数． ⑵ 有理数指数幂的运算性质同样适用于无理数指数幂．10．一般地，当0a >，α为任意实数值时，实数指数幂a α都有意义． 对任意实数α，β，上述有理指数幂的运算法则仍然成立．（二）典例分析【例1】求下列各式的值：⑴；⑵⑶⑷)a b<；⑸．⑹238；⑺1225-；⑻512-⎛⎫⎪⎝⎭；⑼341681-⎛⎫⎪⎝⎭．【例2】计算下列各式：⑴⑵111344213243(,0)6a a ba ba b---⎛⎫-⎪⎝⎭>-．【例3】用分数指数幂表示下列各式（其中各式字母均为正数）：⑴；⑶54m⋅．【例4】，则实数a的取值范围是（）A．a∈R B．12a=C．12a>D．12a≤【例5】设ab=c a，b，c的大小关系是（）【例6】设1120082008(N)2n na n-+-=∈，那么)na-的值是（）【例7】若()x f x =，求10001()1001i i f =∑【例8】 已知210x x +-=，求847x x +的值．【例9】 下列判断正确的有①有理数的有理数次幂一定是有理数 ②有理数的无理数次幂一定是无理数 ③无理数的有理数次幂一定是有理数 ④无理数的无理数次幂一定是无理数 A ．3个B ．2个C ．1个D ．0个板块二：指数函数及其性质（一）知识内容1．指数函数：一般地，函数x y a =(0a >，1a ≠，R)x ∈叫做指数函数． 2．指数函数的图象和性质对比3．x y a =（0a >且1a ≠）的图象特征：1a >时，图象像一撇，过点()0,1，且在y 轴左侧a 越大，图象越靠近y 轴（如图1）； 01a <<时，图象像一捺，过点()0,1，且在y 轴左侧a 越小，图象越靠近y 轴（如图2）； x y a =与x y a -=的图象关于y 轴对称（如图3）．图1 图2 图3（二）主要方法：1．指数方程，指数不等式：常要转化为同底数的形式，在利用指数函数的单调性求解； 2．确定与指数有关的函数的单调性时，常要注意针对底数进行讨论； 3．要注意运用数形结合思想解决问题．（三）典例分析：【例10】 已知1a b c >>>，比较下列各组数的大小：①___bca a ；②1ba ⎛⎫⎪⎝⎭1ca ⎛⎫ ⎪⎝⎭；③11___b ca a ；④__a abc ．【例11】 （2009年江苏卷）已知51a -=函数()x f x a =，若实数m n ，满足()()f m f n >，则m n ，的大小关系为 ．【例12】 图中的曲线是指数函数x y a =的图象，已知a 取4133,,,3105四个值，则相应于曲线1234,,,c c c c 的a 依次为_______________．【例13】 求下列函数的定义域、值域⑴112x y -= ； ⑵3x y -=； ⑶2120.5x x y +-=c 4c 3c 2c 1P 4P 3P 2P 11Oy x板块三：指数函数和其它函数的运算与复合（一）知识内容：复合函数的单调性与奇偶性，重点研究学生熟悉的二次函数的复合，复合函数单调性的判断是重点也是难点．1．和差函数的单调性两个增函数（或减函数）的和仍为增函数（或减函数），一个增函数（或减函数）减去一个减函数（或增函数），结果是一个增（或减）函数． 2．复合函数[()]f g x 的奇偶性、单调性有如下规律：值得注意的是，当且仅当外层函数()f u 的定义域与内层函数()g x 的值域的交集非空时才能构成复合函数[()]f g x ，复合函数奇偶性：两奇才为奇； 复合函数单调性：同增异减（二）典例分析：【例14】 已知2()82f x x x =+-，2()(2)g x f x =-，则()g x 在（ ）A ．(2,0)-上为增函数B ．(0,2)上为增函数C ．(1,0)-上为减函数D ．(0,1)上为减函数【例15】 函数221()3x xf x -⎛⎫= ⎪⎝⎭的单调增区间为_________，值域为___________．【例16】 求函数11()1([3,2])42xxf x x ⎛⎫⎛⎫=-+∈- ⎪ ⎪⎝⎭⎝⎭的单调区间及其值域．【例17】 求下列函数的单调区间．⑴232xx y a -++=（0a >，且1a ≠）；⑵已知910390x x -⨯+≤，求函数1111()4()542x x y --=-⋅+最值．【例18】 （2007-2008北京四中期中测试）求函数1()423x x f x a +=-⋅+ (R)x ∈的值域．【例19】 已知11()212x f x x ⎛⎫=+ ⎪-⎝⎭．⑴求证：()0f x >；⑵若()()()F x f x t f x t =++-（t 为常数），判断()F x 的奇偶性．【例20】 讨论函数21()21x x f x -=+的奇偶性、单调性，并求它的值域．【例21】 已知函数2()()1x x af x a a a -=--，其中0a >，1a ≠．⑴判断函数()f x 的奇偶性； ⑵判断函数()f x 的单调性，并证明．【例22】 （2008-2009南通一中高三期中考试题）在计算机的算法语言中有一种函数[]x 叫做取整函数（也称高斯函数），它表示x 的整数部分，即[]x 是不超过x 的最大整数．例如：[2]2=，[3.1]3=，[ 2.6]3-=-．设函数21()122x xf x =-+，则函数[()][()]y f x f x =+-的值域为（ ）【例23】 （2008-2009首师大附中高中课改数学模块1水平监测期中考试）因为复杂的函数，往往是由多个简单函数的加、减、乘、除运算得到，或者是多个函数的复合后得到的，比如下列函数：()()()22x f x g x h x x ==，，则()()f x g x ，复合后可得到函数()()2x g f x g =⎡⎤⎣⎦()f g x f ==⎡⎤⎣⎦个函数的自变量的取值，得到的函数称为复合函数；也可以由()()f x g x ，进行乘法运算得到函数()()2x f x g x =．所以我们在研究较复杂的函数时，常常设法把复杂的函数进行逆向操作，把其拆分转化为简单的函数，借助简单函数的性质进行研究．⑴复合函数(){}f h g x ⎡⎤⎣⎦的解析式为 ；其定义域为 ．⑵可判断()()2x f x g x =是增函数，那么两个增函数相乘后得到的新函数是否一定是增函数？若是请证明，若不是，请举一个反例；⑶已知函数()2x f x -=，若()()121f x f x +>-，则x 的取值范围为 ．⑷请用函数()()()()22ln x f x g x h x x k x x ====，，中的两个进行复合，得到三个函数， 使它们分别为偶函数且非奇函数、奇函数且非偶函数、非奇非偶函数．【例24】 设a ∈R ，2()()21xf x a x =-∈+R ，若()f x 为奇函数，求a 的值．【例25】 小明即将进入一大学就读，为了要支付4年学费，小明欲将一笔钱存入银行，使得每年皆有40000元可以支付学费．而银行所提供的年利率为6%，且为连续复利，试求出小明现在必须存入银行的钱的数额．习题1. 比较下列各题中两个值的大小：⑴ 2.51.7，31.7； ⑵ 0.10.8-，0.20.8-； ⑶ 0.31.7， 3.10.9．习题2. （2007年山东潍坊统考）若1a >，0b >，且22b b a a -+=，则b b a a --的值为（ ）A ．6B ．2或2-C ．2-D ．2习题3. 函数()342x x f x =⋅-，求()f x 在[0,)x ∈+∞上的最小值．习题4. 化简：⑴111()()()a b c a b c ab ca bc a b cxxx------⋅⋅ ⑵a b b c c a c a a b b c b c c a a b x x x ------+++⋅⋅．家庭作业习题5. 已知1010()1010x xx xf x ---=+，判断函数的单调性、奇偶性，并求()f x 的值域．习题6. 已知2()()(0,1)2x x af x a a a a a -=->≠-是R 上的增函数，求a 的取值范围．习题1. 函数||()x f x e =（ ）A ．是奇函数，在(,0]-∞上是减函数B ．是偶函数，在(,0]-∞上是减函数C ．是奇函数，在[0,)+∞上是增函数D ．是偶函数，在(,)-∞+∞上是增函数习题2. 方程2x =2-x 的解的个数为______________．习题3. 已知函数|22|x y =-，⑴ 作出函数的图象；⑵ 根据图象指出函数的单调区间；⑶ 根据图象指出当x 取什么值时，函数有最值．月测备选。

第一节指数与指数函数、幂函数复习目标学法指导1.指数函数(1)指数与指数幂的运算①根式的意义.②分数指数幂的意义.③无理数指数幂的意义.④有理数指数幂的运算性质.(2)指数函数及其性质①指数函数的概念.②指数函数的图象.③指数函数的性质.了解函数图象的平移与对称变换,体会数学的逼近、数形结合等思想. 2.幂函数(y=x,y=x2,y=x3,y=12x,y=x-1)(1)幂函数的概念.(2)幂函数的图象.(3)幂函数的性质. 1.明确根式与分数指数幂的意义,能互相转化.2.有理数指数幂的运算以同底为基本条件.3.指数函数与幂函数的概念及形式概念,要从解析式的系数、底数、指数、常数等方面去理解与把握其要求.4.运用指数函数的图象与性质能解决幂值的大小比较、指数不等式的求解、参数的取值范围的确定等问题.一、根式与指数幂 1.根式 n 次方 根如果x n =a,那么x 叫做a 的n 次方根,其中n>1,n ∈N *当n 是奇数时,a 的n 次方根x=na当n 是偶数时,正数a 的n 次方根x=±na(a>0);负数的偶次方根没有意义0的任何次方根都是0,记作0n=0式子na叫做根式,其中n 叫做根指数,a 叫做被开方数当n 为任意正整数时,(na)n =a当n 为奇数时,nn a =a当n 为偶数时,nna =|a|=(0)(0)a a a a ≥⎧⎨-<⎩ 2.有理数指数幂正分数指数幂:m na =nmaa>0,m,n ∈N *,且n>1负分数指数幂:mna -=1m na=1nma0的正分数指数幂等于0;0的负分数指数幂没有意义a r ·a s =a r+sa>0,b>0,r,s ∈Q(a r)s=a rs(ab)r =a r b r3.无理数指数幂无理数指数幂aα(a>0,α是无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.1.公式理解(1)n a中a 的取值取决于n(n ∈N*)的奇偶,当n为奇数时,a∈R;当n 为偶数时,a≥0.(2)n n a的值取决于n(n∈N*)的奇偶,必要时需分类讨论.2.与指数幂的运算性质有关的结论由负指数幂的定义可知:(1)a r÷a s=a r-s;(2)s r a=1()r sa=r s a.二、指数函数的概念、图象与性质函数y=a x(a>0,且a≠1)图象0<a<1 a>1图象特征在x轴上方,过定点(0,1)当x逐渐增大时,图象逐渐下降当x逐渐增大时,图象逐渐上升性质定义域R值域(0,+∞)单调性递减递增函数变化规律当x=0时,y=1当x<0时,y>1;当x>0时,0<y<1当x<0时,0<y<1;当x>0时,y>11.概念理解(1)指数函数的定义是形式定义,其解析式特征为①系数为1;②底数a>0且a≠1;③无常数项;④指数为自变量x.符合以上特征才为指数函数,否则为指数型函数,如y=2x+1,y=-3x,y=(14)x+1等均为指数型函数y=Aa x+B.(2)由定义可知,解析式中只有一个参数a,所以只需已知函数图象上一点坐标即可确定指数函数.2.与指数函数图象相关的结论①指数函数图象之间的位置关系:在y轴右侧,图象越高,对应的底数越大.如图所示,直线x=1与图象交点的纵坐标即为各自底数的值.②画指数型函数f(x)=Aa x+B的图象时,注意标明渐近线,即在变换指数函数y=a x的图象的同时,渐近线x轴也应随之变换,以便准确应用图象.③底数互为倒数的指数函数的图象关于y轴对称.④画指数函数图象应抓住三个关键点:(1,a),(0,1),(-1, 1a).三、幂函数1.幂函数的概念形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α为常数.2.常见幂函数的图象与性质函数图象或性质y=x y=x2y=x3y=12x y=x-1图象定义域R R R [0,+∞)(-∞,0)∪(0,+∞) 值域R [0,+∞) R [0,+∞)(-∞,0)∪(0,+∞) 奇偶性奇偶奇非奇非偶奇单调性增x∈[0,+∞)时,增;x∈(-∞,0]增增x∈(0,+∞)时,减;x∈(-∞,0)时,减时,减特殊点(1,1)(0,0)(-1,-1)(1,1)(0,0)(-1,1)(1,1)(0,0)(-1,-1)(1,1)(0,0)(1,1)(-1,-1)1.概念理解(1)幂函数的定义是形式定义,其解析式特征为①系数为1;②底数只能是自变量x;③指数为常数;④无常数项.(2)由定义可知,幂函数解析式中只有一个参数,所以只需已知函数图象上一点坐标即可确定幂函数.2.与幂函数图象相关的结论(1)幂函数图象可分为三类①α>1,其图象在第一象限是“站立型”的;②0<α<1,其图象在第一象限是“趴型”的;③α<0,其图象在第一象限是“躺型”的,如图所示.(2)幂函数的图象都过定点(1,1),当α>0时,还过定点(0,0),α<0时,一定不过点(0,0),且以坐标轴为渐近线.(3)幂函数图象一定会出现在第一象限,一定不会出现在第四象限,是否出现在二、三象限,取决于函数的奇偶性.3.与幂函数性质相关的结论单调性:当α>0时,在(0,+∞)上为增函数;当α<0时,在(0,+∞)上为减函数.1.(2019·全国Ⅰ卷)已知a=log 20.2,b=20.2,c=0.20.3,则( B ) (A)a<b<c (B)a<c<b (C)c<a<b (D)b<c<a 解析:取中间值.220.200.30log 0.2log 100,2211,00.20.2101,a ab bc c =<=⇒<⎧⎪=>=⇒>⎨⎪<=<=⇒<<⎩⇒a<c<b. 故选B.2.函数f(x)=e |x-1|的单调递减区间是( C ) (A)(-∞,+∞) (B)[1,+∞) (C)(-∞,1] (D)[0,+∞)3.已知函数f(x)= 1,1,1(),1,2x x x x -≤⎧⎪⎨>⎪⎩则f(f(2))= ,不等式f(x-3)<f(2)的解集为 .解析:f(2)=(12)2-1=12,f(12)=12,f(f(2))= 12, 当x-3>1,即x>4时,(12)x-3-1<12, 解得x>5,当x-3≤1,即x ≤4时,x-3<12,解得x<72, 所以f(x-3)<f(2)的解集为(-∞,72)∪(5,+∞). 答案:12 (-∞,72)∪(5,+∞)4.若幂函数y=(m 2-3m+3)22m m x --的图象不经过原点,则实数m 的值为 .解析:因为函数为幂函数, 所以m 2-3m+3=1, 解得m=1或m=2. 又因为图象不经过原点, 所以m 2-m-2<0, 所以m=1. 答案:15.(2018·浙江嘉兴模拟)已知函数f(x)=log 4(4-|x|),则f(x)的单调递增区间是 .解析:令t=4-|x|,由于4-|x|>0,所以原函数的定义域为(-4,4),y=log 4t 在定义域上单调递增,而t=4-|x|在(-4,0)上单调递增,在(0,4)上单调递减,根据复合函数的单调性知f(x)=log 4(4-|x|)在(-4,0)上单调递增,在(0,4)上单调递减,故原函数的单调递增区间为(-4,0). 答案:(-4,0)考点一 根式与指数幂的运算 [例1] 求值与化简:(1)133()2-×07()6-+148423236232()3-(2)352a b ·53343b a .解:(1)原式=132()3×1+342×142+(132×123)6-132()3=2+4×27 =110. (2)352a b·53343b a=33212a-·321510b-=54a =a4a.指数幂的运算顺序及注意事项(1)有括号的先算括号里的,无括号的先做指数运算. (2)先乘除后加减,负指数幂化成正指数幂的倒数.(3)底数是负数,先确定符号;底数是小数,先化成分数;底数是带分数,先化成假分数.(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.提醒:运算结果不能同时含有根号和分数指数,也不能既有分母又含有负指数.若f(x)符合:对定义域内的任意的x 1,x 2,都有f(x 1)f(x 2)=f(x 1+x 2),且当x>1时,f(x)<1,则称f(x)为“好函数”,则下列函数是“好函数”的是( B )(A)f(x)=2x (B)f(x)=(12)x(C)f(x)=12log x (D)f(x)=log 2x解析:对定义域内的任意的x1,x2,都有f(x1)·f(x2)=f(x1+x2),说明函数是指数函数,排除选项C,D;又因为x>1 时,f(x)<1,所以排除选项A.故选B.考点二幂、指数函数的图象及应用[例2] (1)幂函数y=f(x)的图象经过点(4,2),则f(x)是( )(A)偶函数,且在(0,+∞)上是增函数(B)偶函数,且在(0,+∞)上是减函数(C)奇函数,且在(0,+∞)上是减函数(D)非奇非偶函数,且在(0,+∞)上是增函数(2)图中曲线是幂函数y=xα在第一象限的图象.已知α取±2,±12四个值.则相应于曲线C1,C2,C3,C4的α值依次为.解析:(1)设幂函数f(x)=xα,代入点(4,2),4α=2,α=12,所以f(x)=12x x则f(x)是非奇非偶函数,且在(0,+∞)上是增函数,故选D.(2)由图象特征可知C1的α1>1,C2的α2满足0<α2<1,C3,C4的α3,α4<0,又x=2时,2-2=14<1222,所以α3=-12,α4=-2.答案:(1)D (2)2,12,-12,-2(1)幂函数的指数与图象特征的关系当α≠0,1时,幂函数y=xα在第一象限的图象特征α取值α>1 0<α<1 α<0 图象特殊点过(0,0),(1,1) 过(0,0),(1,1) 过(1,1) 凹凸性下凸上凸下凸单调性递增递增递减举例y=x2y=12x y=x-1,y=12x(2)指数函数图象可解决的两类热点问题及思路①求解指数型函数的图象与性质问题对指数型函数的图象与性质问题(单调性、最值、大小比较、零点等)的求解往往利用相应指数函数的图象,通过平移、对称变换得到其图象,然后数形结合使问题得解.②求解指数型方程、不等式问题一些指数型方程、不等式问题的求解,往往利用相应指数型函数图象数形结合求解.提醒:应用指数函数的图象解决指数方程、不等式问题以及指数型函数的性质,要注意画出的图象的准确性,否则数形结合得到的可能为错误结论.(2018·上海卷)已知α∈(-2,-1,-12,12,1,2,3).若函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α= .解析:由f(x)为奇函数,故只能取-1,1,3,又在(0,+∞)上递减,所以α=-1.答案:-1考点三幂、指数函数的性质及应用[例3] 设y1=40.7,y2=80.45,y3=(12)-1.5,则( )(A)y3>y1>y2(B)y2>y1>y3(C)y1>y2>y3(D)y1>y3>y2解析:因为y1=40.7=21.4,y2=80.45=21.35,y3=(12)-1.5=21.5,又函数y=2x在R上为增函数,且1.35<1.4<1.5,所以21.35<21.4<21.5,即y2<y1<y3.故选A.指数函数的性质及应用问题的常见类型及解题策略(1)比较大小问题,常利用指数函数的单调性及中间值(0或1)法.(2)简单的指数方程或不等式的求解问题.解决此类问题应利用指数函数的单调性,要特别注意底数a的取值范围,并在必要时进行分类讨论.(3)指数型函数中参数的取值范围问题,在解决涉及指数函数的单调性或最值问题时,应注意对底数a的分类讨论.(4)对可化为a2x+b·a x+c=0或a2x+b·a x+c≥0(≤0)的指数方程或不等式,常借助换元法解决,但应注意换元后“新元”的范围.(2019·全国Ⅲ卷)函数y=3222x xx -+在[-6,6]的图象大致为( B )解析:函数y=3222x xx -+是奇函数,且当x>0时,y>0,排除C,D,又f(6)=3662622-⨯+≈7,排除A.故选B.考点四 幂函数单调性的应用[例4] (1)已知y 1=a x ,y 2=b x 是指数函数,y 3=x c ,y 4=x d 是幂函数,它们的图象如图所示,则a,b,c,d 的大小关系为( )(A)a<b<c<d (B)b<a<c<d (C)c<b<a<d (D)c<a<b<d(2)若12(1)a +<12(32)a -,求实数a 的取值范围.(1)解析:因为底数大于1,指数函数是增函数,底数大于0小于1,指数函数是减函数,幂指数大于0,幂函数在(0,+∞)是增函数,幂指数小于0,幂函数在(0,+∞)是减函数,所以观察图象可知,d>1,c<0,0<b<a<1,即c<b<a<d,故选C.(2)解:易知函数y=12x的定义域为[0,+∞),在定义域内为增函数,所以10, 320,132. aaa a+≥⎧⎪-≥⎨⎪+<-⎩解得-1≤a<23.(1)根据幂函数的单调性比较大小①同底不同指、同指不同底的幂值大小比较:幂函数y=xα中指数α的取值直接影响图象和性质,当α的取值不同时,函数的单调性不同,依据图象规律确定单调性后再比较大小.②既不同底又不同指的幂值大小比较常找到一个中间值,通过比较幂值与中间值的大小来判断.(2)与幂函数有关的综合性问题一般是利用单调性、奇偶性以及函数图象求函数值域、不等式解集等.考点五易错辨析[例5] 方程(12)x-1+(14)x+a=0有正数解,则实数a的取值范围是( )(A)(-∞,1) (B)(-∞,-2)(C)(-3,-2) (D)(-3,0)解析:令t=(12)x,因为方程有正根,所以t∈(0,1),t2+2t+a=0有解,所以a=1-(t+1)2.因为t∈(0,1),所以a∈(-3,0).故选D.令t=(1)x易忽视t的范围,误认为t∈(0,+∞),从而导致错2误.(2019·诸暨市期末)函数f(x)满足f(x)≤x2且f(x)≤2x(x∈R),则( D )(A)若f(a)≤b2,则a≥b (B)若f(a)≤2b,则a≤b(C)若f(a)≥b2,则a≤b (D)若f(a)≥2b,则a≥b解析:若f(a)≥2b,则由f(x)≤2x得f(a)≤2a,则2b≤2a,则a≥b,故选D.类型一根式与指数幂的运算1.已知f(x)=2x+2-x,若f(a)=3,则f(2a)等于( B )(A)5 (B)7 (C)9 (D)11解析:由f(a)=3得2a+2-a=3,两边平方得22a+2-2a+2=9,即22a+2-2a=7,故f(2a)=7.故选B.2.(2019·新高考研究联盟)已知方程log a(5x-3x)=x(其中a>0,a≠1),若x=2是方程的解,则a= ;当a=2时,方程的解x= .解析:若x=2是方程的解,则log a(52-32)=log a42=2,所以a=4;当a=2时,log2(5x-3x)=x,即5x-3x=2x,通过对比可知,该方程的解为x=1.答案:4 1类型二幂、指数函数的图象及应用3.已知函数f1(x)=a x,f2(x)=x a,f3(x)=log a x(其中a>0,且a≠1),在同一坐标系中画出其中的两个函数在第一象限内的图象,正确的是( B )解析:由a>0且a≠1知f2(x)=x a的图象过原点,f1(x)=a x的图象过(0,1),f3(x)=log a x的图象过(1,0),可排除A.而f1(x)与f3(x)的单调性相同,排除C,从选项B,D图象知f2(x)=x a中的a>1.故选B.4.(2018·浙江卷)函数y=2|x|sin 2x的图象可能是( D )解析:由y=2|x|sin 2x知函数的定义域为R,令f(x)=2|x|sin 2x,则f(-x)=2|-x|sin(-2x)=-2|x|sin 2x. 因为f(x)=-f(-x),所以f(x)为奇函数. 所以f(x)的图象关于原点对称,故排除A,B. 令f(x)=2|x|sin 2x=0,解得x=π2k (k ∈Z),所以当k=1时,x=π2,故排除C.故选D.类型三 指数函数的性质及应用5.已知函数f(x)=(12)x ,则不等式f(a 2-4)>f(3a)的解集为( B ) (A)(-4,1) (B)(-1,4) (C)(1,4) (D)(0,4)解析:可知函数f(x)为减函数,由f(a 2-4)>f(3a),可得a 2-4<3a, 整理得a 2-3a-4<0,解得-1<a<4,所以不等式的解集为(-1,4). 故选B.6.设y=f(x)在(-∞,1]上有定义,对于给定的实数K,定义f K (x)=(),(),,(),f x f x K K f x K ≤⎧⎨>⎩给出函数f(x)=2x+1-4x ,若对于任意x ∈(-∞,1],恒有f K (x)=f(x),则( D )(A)K 的最大值为0 (B)K 的最小值为0 (C)K 的最大值为1 (D)K 的最小值为1解析:根据给出的定义,f K (x)是在函数y=f(x),y=K 中取较小者,对任意的x ∈(-∞,1]恒有f K (x)=f(x),等价于对任意的x ∈(-∞,1]恒有f(x)≤K,等价于f(x)max ≤K,x ∈(-∞,1]. 令t=2x ∈(0,2],则函数f(x)=2x+1-4x , 即为函数ϕ(t)=-t 2+2t=-(t-1)2+1≤1,故函数f(x)在(-∞,1]上的最大值为1,即K≥1,故选D.7.函数f(x)=a x-b的图象如图所示,其中a,b为常数,则下列结论正确的是( D)(A)a>1,b<0 (B)a>1,b>0(C)0<a<1,b>0 (D)0<a<1,b<0解析:函数f(x)=a x-b在定义域上单调递减,所以0<a<1.函数f(x)=a x-b的图象是在f(x)=a x的基础上向左平移得到的,所以b<0.类型四幂函数单调性的应用8.设函数f(x)=e|ln x|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( C )(A)x2f(x1)>1 (B)x2f(x1)=1(C)x2f(x1)<1 (D)x2f(x1)<x1f(x2)解析:f(x)=1,01, ,1,xxx x⎧<<⎪⎨⎪≥⎩当0<x1<1<x2时,选项A成立; 当0<x2<1<x1时,选项B,D成立, 故选C.类型五易错易误辨析9.若存在正数x使2x(x-a)<1成立,则a的取值范围是( D )(A)(-∞,+∞) (B)(-2,+∞)(C)(0,+∞) (D)(-1,+∞)解析:因为2x>0,所以由2x(x-a)<1,得a>x-(1)x,2)x,令f(x)=x-(12则函数f(x)在(0,+∞)上是增函数,)0=-1,所以f(x)>f(0)=0-(12所以a>-1.故选D.。