当前位置：文档之家 › 应用弹性力学教程第二章

应用弹性力学教程第二章

  • 格式：doc
  • 大小：1.82 MB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

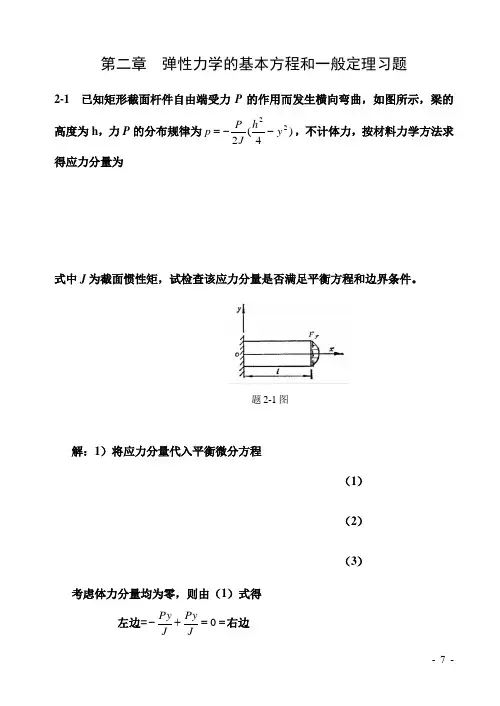
弹性力学第3版王光钦第二章习题解答

弹性力学第3版王光钦第二章习题解答

- 7 -第二章 弹性力学的基本方程和一般定理习题2-1 已知矩形截面杆件自由端受力P 的作用而发生横向弯曲，如图所示，梁的高度为h ，力P 的分布规律为)4(222y h J P p --=，不计体力，按材料力学方法求得应力分量为式中J 为截面惯性矩，试检查该应力分量是否满足平衡方程和边界条件。

解：1）将应力分量代入平衡微分方程 （1） （2）（3）考虑体力分量均为零，则由（1）式得左边===+-0JPy J Py 右边 题2-1图- 8 - 将应力分量代入平衡微分微分方程的（2）、（3），显然平衡微分方程满足。

2）应力边界条件 n m l T zx yx x x ττσ++= （4） n m l T zy y xy y τστ++= （5）n m l T z yz xz z σττ++=（6）这里必须注意：应力边界条件必须满足所有的边界，而不是仅仅求出待定常数。

下面考虑上边界 i ）上边界0,1,0===n m l ，0,0,0===z y x T T T将上式代入（4）、（5）、（6）式，得0)(2==hy yx τ 0)(2==h y y σ 0)(2==h y yz τ上式就是简化后的边界条件。

必须强调的是：在考察边界条件时，需将已知的边界坐标值代入表达式。

将应力分量代入上面三式，显然三式成立。

ii ）下边界0,1,0=-==n m l ，0,0,0===z y x T T T将上式代入（4）、（5）、（6）式，得0)(2=-=hy yx τ 0)(2=-=h y y σ 0)(2=-=h y yz τ将应力分量代入上面三式，显然三式成立。

- 9 -iii ）右边界0,0,1===n m l ，,0=x T )4(222y h J P T y --=0,=z T 应注意：所有的面力都是与坐标正向一致为正。

将上式代入（4）、（5）、（6）式，得0)(==l x x σ)4(2)(22y h J P lx xy --==τ0)(==l x xz τ同样，在检验边界条件时，应该将l x =的值代入，显然三式成立。

同济大学弹性力学第二章-修改20140226

同济大学弹性力学第二章-修改20140226

第二章 应力状态理论
2.1 体力和面力 2.2 应力和一点的应力状态 2.3 与坐标倾斜的微分面上的应力 2.4 平衡微分方程 应力边界条件 2.5 转轴时应力分量的变换 2.6 主应力 应力张量不变量 2.7 最大切应力
第二章 应力状态理论
弹性力学研究的都是超静定问题，故而必 须从静力学、几何学和物理学三个方面一起考 虑。
2.4 平衡微分方程 应力边界条件
B
B A
A
物体受外力作用处于平衡状态也保证了单元体的平衡 分别在物体内取任意一个平行六面体和四面体分析其平衡
z
考虑 Fx 0 ，有
z z dz
z zy zy dz
z
(x x dx)dydz xdydz (yx yx dy)dxdz
x
y
yx
y
zx zx dz
fz xzl yzm zn
2.5 转轴时应力分量的变换
z
c
f xz
x’
M
f xy
O
f xx
b
y’ a
z’
x
ij yxx
xy y
xz yz
zx zy z
y
？
x xy xz
ij yx
y
yz
zx zy z
x
xl12
ym12
zn12
2
yzm1n1
Fz 0
Mx 0
My 0
Mz 0
z
z z dz z
zy zy dz z
yx
zx zx dz z
xy
x yz yz dy
y
xz xz dx
y
x xz
xy xy dx x
y y dy
弹性力学简明教程 第2章 平面问题的基本理论

弹性力学简明教程 第2章 平面问题的基本理论


一 、求AB面上的正应力σn和切应力τn
设px、py为斜面AB的应力p在x、y 轴上的投影。斜面 AB的长度为 ds, 则AB=ds, PB=lds, PA=mds 。 由平衡条件∑Fx=0 得：
l ds m d s p x ds x l ds xy m ds f x 0 2
除以ds ,然后令ds→0, 得：
B'
一、位移与形变
刚体位移
如果各点(或部分点）间的相对距离发生变化， 则物体发生了变形。这种变形一方面表现在微 线段长度的变化，称为线应变；一方面表现在 微线段间夹角的变化，称为切应变。
O
A
O
A'
B
B'
二、几何方程
几何方程——描述任一点的微线段上形变分量 与位移分量之间的关系。 P点的形变分量与位移分量的关系？
0 l 1
当 l2 = 1 时，
0 l 2 1
n nmax 1 ( 1 2 ) 2 1
当 l2 = 0 时，
n n min 2
可见：两个主应力就是最大与最小的正应力。
五、求最大与最小的切应力
任意斜面上的切应力 n lm( y x ) (l 2 m 2 ) xy
y
二、几何方程
PA的线应变在小变形
时是由x 方向的位移 引起的，因此PA的线 应变为
P' A' PA x PA
o u
P
x
u
dx
v
P'
A
u dx x

A'
v
v dx x
y
u (u dx) u AA' PP' u x dx PA x v (v dx) v v x PA的转角为 dx x
弹性力学 第二章

弹性力学 第二章

( x, y ) 1 2 ( x, y ) ( x dx, y ) ( x, y ) dx (dx) 2 2 x 2 x ( x, y ) ( x, y ) dx x
( x, y ) ( x, y dy ) ( x, y ) dy y
弹性力学 第二章 12
( x y xy )
2.2 Differential equations of equilibrium 平衡微分方程 • Equations of equilibrium in mechanics of materials 材料力学中的平衡方程 isolated element (脱离体) L×h×b 从整体平衡中可求得反力 X×h×b 从部分梁的平衡可求得内力， dx×h×b 从dx×h的脱离体平衡可求得M、Q和q
• a spatial problem a plane problem the body has a particular shape. particular external forces. • 当物体的形状特殊，外力分布特殊，空间问题 转化为平面问题。 • Plane problems: plane stress problems and plane strain problems 平面问题: 平面应力问题与平面应变问题
yx y
xy x
By taking moments of all the forces about an axis parallel to the z axis at the midpoint C ,we have,
dx
M
C
0
yx
dy
y
y
y y
( xy ( yx
弹性力学讲义第2章(p)

弹性力学讲义第2章(p)


zx 0
切应力互等
yz 0 xz 0
只剩平行于x y面的三个应力分量: x , y , xy
§ 2-1 平面应力问题与平面应变问题
u, v, w 非独立变量
t/2
t/2
x, y, z zx zy 0, xy
平面应力问题 ——
只有平面应力分量 x , y , xy yx 存在且仅
x
1 E
x
y
y
1 E
y
x
z
E
( x
y)
xy
2(1)
E
xy
yz 0
zx 0
z ( x y )
x
1 E2(Fra bibliotekx1
y
)
y
1 E
2
(
y
1
x
)
xy
2(1 E
)
x
y
§2-4 物理方程
平面应力问题:
平面应变问题:
E
剪切模量转换形 式同样是不变的
E
12
1
1 G
2(1)
E
2(1 1 E
试证明图中y方向的位移v 所引起的线段PA
的伸缩是高阶微量。
一点的应变位移关系——切应变
求线段PA与PB之间的直角的改变, 也就是切应变 xy,用位移分
量来表示。
v
v x
dx
v
v
dx
x
u
y
切应变
xy
v x
u y
0
u
u u dx
P
dx A x
v P
dy
B
v v dy
A
y
B
y
清华大学_弹性力学_第二章_应力理论_习题答案

清华大学_弹性力学_第二章_应力理论_习题答案

第二章知识点： （1）应力矢量()0limS FSνσ∆→∆∆其中，ν是S ∆的法向量（2）应力张量()()()111121321222323132333σσσσσσσσσσσσσ⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭其中，()()()123,,σσσ 分别是123,,e e e方向的应力矢量，且()()()111122133121122223323113223333e e e e e e e e e σσσσσσσσσσσσ=++=++=++上式可以写为张量形式ij i j e e σσ=或者用正应力剪应力将应力张量写为x xy xz yx y yz zx zy z σττστστττσ⎛⎫ ⎪= ⎪ ⎪⎝⎭（3）柯西公式（应力矢量和应力张量的关系）()νσνσ=⋅其中，ν是斜面的法向量，对于表面来说，就是外法向量。

可以将柯西公式写成如下形式()i i mj m j i mj i m j i mj im j i ij j e e e e e e e e νσνσνσνσνσδνσ=⋅=⋅=⋅== 即()i ij j νσνσ=这其实是三个式子，分量形式为()()()111122133112112222332231132233333++++i i i i i i νννσνσνσνσνσσνσνσνσνσσνσνσνσνσ==++====在表面上，所求出的()νσ就是外载荷。

（4）应力张量的转轴公式''''m n ij m i n j σσββ=证明如下：'''''''''''''''''''',ij i j m n m n i m i m j n j n ij m i n j m n m n m n m n ij m i n je e e e e e e e e e e e σσσββσββσσσββ====∴=∴=也可以将转轴公式写为矩阵形式[][][][]'Tσβσβ=其中，[]σ、[]'σ是坐标系变换前后的应力张量的分量，[]()'m i ββ=，'m i β是i e 在'm e上的分量，可以用如下公式计算()''cos ,m ii m e e β=（5）剪应力互等定理根据微元体的力矩平衡，可以得到 ,,yz zy xz zx xy yx ττττττ===也就是说ij ji σσ=应力张量是一个二阶对称的张量 （6）主应力由于应力张量是二阶对称的，所以可以将其对角化[][][]123Tσσβσβσ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦并且123,,σσσ从大到小排列，他们称为主应力，[]β是三个主应力的方向。

弹性力学课后答案

弹性力学课后答案

弹性力学课后答案第二章习题的提示与答案2－1是2－2是2－3按习题2－1剖析。

2－4按习题2－2剖析。

2－5在的条件中，将出现2、3 阶微量。

当略去 3 阶微量后，得出的切应力互等定理完整相同。

2－6同上题。

在平面问题中，考虑到3阶微量的精度时，所得出的均衡微分方程都相同。

其差别不过在 3 阶微量（即更高阶微量）上，能够略去不计。

2－7应用的基本假定是：均衡微分方程和几何方程─连续性和小变形，物理方程─理想弹性体。

2－8 在大界限上，应分别列出两个精准的界限条件；在小界限（即次要界限）上，依据圣维南原理可列出 3 个积分的近似界限条件来取代。

2－9在小界限OA边上，对于图2－15（a）、（b）问题的三个积分界限条件相同，所以，这两个问题为静力等效。

2－10拜见本章小结。

2－11拜见本章小结。

2－12拜见本章小结。

2－13注意按应力争解时，在单连体中应力重量一定知足（1）均衡微分方程，（2）相容方程，（3）应力界限条件（假定 ) 。

2－14赐教科书。

2－152－ 16赐教科书。

赐教科书。

2－17取它们均知足均衡微分方程，相容方程及x=0 和的应力界限条件，因此，它们是该问题的正确解答。

2－18赐教科书。

2－19提示：求出任一点的位移重量和，及转动量，再令, 即可得出。

第三章习题的提示与答案3－1此题属于逆解法，已经给出了应力函数，可按逆解法步骤求解：（1）校核相容条件能否知足，（2）求应力，（3）推求出每一边上的面力进而得出这个应力函数所能解决的问题。

3－2用逆解法求解。

因为此题中l>>h, x=0,l属于次要界限（小界限），可将小界限上的面力化为主矢量和主矩表示。

3－3见3-1例题。

3－4此题也属于逆解法的问题。

第一校核能否知足相容方程。

再由求出应力后，并求对应的面力。

此题的应力解答如习题3-10 所示。

应力对应的面力是：主要界限：所以在界限上无剪切面力作用。

下界限没法向面力；上界限有向下的法向面力 q。

弹性力学第二章_4

弹性力学第二章_4


D
F
∂f x ∂f y ∂2 ∂2 ( 2 + 2 )(σ x + σ y ) = −(1 + µ ) 平面应力） ∂x + ∂y （平面应力） ∂x ∂y
应力法的方程（平面应力状态）： 应力法的方程（平面应力状态）：
∂σ x ∂τ xy + + fx = 0 ∂x ∂y
∂ Φ σ y = 2 − f y y, ∂x
2
∂Φ τ xy = − ∂x∂y
2
式中: Φ 称为应力函数，又称Airy函数。
第二章 平面问题的基本理论
将以上通解代入（3），得：
∂ 2Φ ∂ 2Φ ∂ ∂ ( − f x x + 2 − f y y) = 0 ( 2 + 2) 2 ∂y ∂x ∂x ∂y
必存在函数A(x,y) 必存在函数
∂A σ x −V = ∂y
− τ xy
∂A = ∂x
由（2）得必存在函数 ）得必存在函数B(x,y)
∂B σ y −V = ∂x
− τ xy
∂B = ∂y
同理得必存在函数Φ 同理得必存在函数Φ(x,y)
∂Φ A= ∂y
∂Φ B= ∂x
得:
∂Φ σ x = 2 +V ∂y
依据偏微分方程理论，则必存在A(x,y)，使
∂A σx = , ∂y
− τ xy
∂A = ∂x
同样，将方程（5）写作：
∂σ y
∂ (− τ xy ) = ∂y ∂x
第二章 平面问题的基本理论
∂B , 则必存在B(x,y)，使 σ y = ∂xB = ∂x ∂y
第二章 平面问题的基本理论
如果体力是有势的力，即可以表示为： 例：如果体力是有势的力，即可以表示为：
弹性力学简明教程(第四版)第二章课后习题答案

弹性力学简明教程(第四版)第二章课后习题答案


所以
0
g y h1
0
s
gh1
代入公式（2-15）得 ①在主要边界上 x=0，x=b 上精确满足应力边界条件：
x x 0 g ( y h1 ), xy x 0 0; x x b g ( y h1 ), xy x b 0;
第二式 自然满足 将应力分量代入相容方程（2-23）
满足
2 2 xy xy 左 2 2 x y 12q. 3 12q. 3 0 右 y lh lh x
应力分量不满足相容方程。 故，该分量组分量不是图示问题的解答。 2-16：设已求得一点处的应力分量，试求 1 , 2 ,
第二章：平面问题的基本理论
2-8： 在图 2-16 中， 试导出无面力作用时 AB 边界上的 x , y , xy 之间的关系式。 解答：由题可得：
l cos , m cos 90 sin f x AB 0, f y AB 0
将以上条件代入公式（2-15） ，得：
⑵图 2-18 ①上下主要边界 y=-h/2，y=h/2 上，应精确满足公式（2-15）
l
y h 2 h y 2
m
-1 1
f x (s)
0 - q1
f y (s)
0 0
q
0
(y)y-h/2 q， (yx)y-h/2 0， (y)yh/2 0， (yx)yh/2 q 1
3q xy xy 3 . 2q 3 A 2 lh lh
得：
根据边界条件

y
y h / 2
0
q x A . 2 l
得
故
第二章弹性力学基础2.ppt

第二章弹性力学基础2.ppt

理。在图1-8a中的P A和P B所作的功就不是发生在它本身
(状态a)的位移上，(因为它本身是平衡的不存在位移)，而 是在状态(b)的位移上作的功。可见，这个位移对于状态(a) 来说就是虚位移，亦即是状态(a)假象的位移。
重庆交通大学
虚功原理
必须指出，虚功原理的应用范围是有条件的，它所涉及到的两 个方面，力和位移并不是随意的。对于力来讲，它必须是在位 移过程中处于平衡的力系；对于位移来讲，虽然是虚位移，但 并不是可以任意发生的。它必须是和约束条件相符合的微小的 刚体位移。
h
的下自由表面上，f x
(s)
fy (s) 0
方向余弦l 0, m 1, 代入(2—15)
xy 0 ， y 0
3，在 y 1 h 的上表面上，x处 2
f
x
(
s)
0，f
y
(
s)
1 l
qx
方向余弦l 0, m 1, 代入(2—15)
xy 0
y
1 qx l
重庆交通大学
4，x l 的固定端是位移边界条件， 有u v 0 (w 0)
§3.2 边界条件
表示弹性体在边界上位移与约束、或者应力与面力间的关 系式。分为：位移边界条件，应力边界条件，混合边界条件
1、位移边界条件：如在弹性体部分边界 su 上给定约束位移
分量 u (s) 和 v (s) ，则对于此边界上的每一点，位移函
数 u 和 v 应该满足条件
(u)s u(s)， (v)s v (s) （在Su上）
圣维南原理可以大大简化局部边界上的应力边界条 件，为计算带来了很大便利。
重庆交通大学
F
F
F
F/2 F/2
F/2
弹性力学课件第二章

弹性力学课件第二章


定义
§2－2 平衡微分方程
平衡微分方程--表示物体内任一点的 微分体的平衡条件。
第二章 平面应力问题和平面应变问题
定义
在任一点（x，y）取出一微小的平行六面 体 dxd,y作1 用于微分体上的力：
体力： f x , 。f y
应力：作用于各边上， 并表示出正面上 由坐标增量引起 的应力增量。
第二章 平面应力问题和平面应变问题
平面应变
简化为平面应变问题：
（1）截面、外力、约束沿z 向不变，外力、约束
平行xy面，柱体非常长；
故任何z 面（截面）均为对称面。
w 0, 只有u,v; （平面位移问题）
w 0 εz 0,
τ zx , τ zy 0 zx , zy 0,
只有 x , y , xy .
（平面应变问题）
第二章 平面应力问题和平面应变问题
应用的基本假定： 连续性假定─应力用连续函数来表示。 小变形假定─用变形前的尺寸代替变
形后的尺寸。
第二章 平面应力问题和平面应变问题
平衡条件
列出平衡条件：
合力 = 应力×面积，体力×体积； 以正向物理量来表示。
平面问题中可列出3个平衡条件。
第二章 平面应力问题和平面应变问题
平衡条件
Fx 0,
(σ
表示，用于按位移求解。
第二章 平面应力问题和平面应变问题
平面应力
平面应力问题的物理方程：
代入 σz zx ，得zy ： 0
x
1 E
(σ x
σ y ),
xy
2(1 E
) xy.
y
1 E
(σ y
σ
x
),
(a)
在z方向 σ z 0,

弹性力学徐芝纶版第二章

l 1 nmax 1 l 0 nmin 2
第二章 平面问题的基本理论
试用两个主应力表示出任意截面的切应力， 并求最大切应力的值。
N lm( y x ) l2 m2 xy
解：取 x 1, y 2, xy 0
us u, vs v
如图： (u)xa 0
3．混合边界条件 在边界S上同时有：
l x s m xy s fx
us u, vs v
oa
x
y
l( xy)s m( y )s f y
第二章 平面问题的基本理论
1.物体的一部分边界上具有已知位移，因而具有位
第二章 平面问题的基本理论
解：（1）由公式得：
1

100 2
50


100

50
2




10
2
50
150MPa
2
2

100 50 2


100

50
2




10
2
50
0MPa
2
tg1
150 100 10 50
0.707 ,1

35o16 '
则任意截面上有： N lm( 2 1)
N lm( 2 1) l 1 l 2 2 1

1 4

(
1 2

l
2
)2

2

1

所以在
1 l2 0 2
时取得极值：
N
max

弹性力学PPT课件


(2) z 0
z



E
( x

y)
（2）平面应变问题的物理方程
由于平面应变问题中 z yz zx 0
x

1 E
x
( x
z)
由式（2-13）第三式，得 z ( x y )
x

1 2
E
(
x

1


y)
y
zx
2
z t 0 2
沿 z 轴方向不变。 可认为整个薄板的
zy z t 0 各点都有：
z 0
zx 0 zy 0
y
a
y
2
由剪应力互等定理，有
zx
xz

0
zy
yz

0 y
结论： 平面应力问题只有三个应力分量：
yx
x x (x, y) y y (x, y) xy yx xy (x, y)
§2-2 平衡微分方程
基本思路：过弹性体内任意一点P截取一微小的正平行六面体
（微分体） 把应力（内力）和体力（外力）作用在该微
分体上
考虑其平衡，列出力的平衡条件
得到平
衡微分方程
2.2 平衡微分方程
x 平面问题的平衡微分方程： O
注：这xyxx里xxy 用y了x小yyyxy变形YX假定00、（连2续-2）性假定yyx和均匀xyy性x xdP假yBy定Dy。YyXyCxAyy xxdyyxxxxydxdx
0
2u
热传导方程（热力学、扩散问题）：
x
2

2u y 2

弹性力学第02章3


应用圣维南原理后的积分边界条件具体表达式为：
h/2 h/ 2
(x
)xl
dy1

h/ 2 h/ 2
fx ( y)dy1
h/2
( ) h/2
x xl
ydy1
h/ 2 h/ 2
fx ( y) ydy1
h/2
( ) h/2 xy xl
§2.6 平面问题的边界条件
边界条件：表示边界上位移与约束，或应力与面
力之间的关系式，又分为位移边界条件、应力边界 条件和混合边界条件。
1、位移边界条件：若给定了部分边界上的约束位移 分量，则边界上每一点的位移函数应满足如下条件
( u )s u ( s ),()s( s )
其中等式左边是位移的边界值，而等式右边则是边界 上的约束位移分量，是边界上坐标的已知函数。对于 完全固定的边界，其约束位移分量均为0。
平面问题的边界条件
由上可知，应力边界条件可采用两种表达形式：
1、在边界上取出一个微分体，考虑其平衡条件，便可 得出应力边界条件（2-15）或其简化式； 2、在同一边界面上，应力分量应等于对应的面力分量 （数值相同，方向一致）。由于面力的数值和方向是给 定的，因此，在同一边界面上，应力的数值应等于对应 的面力的数值，而面力的方向就是应力的方向。例如：
圣维南原理及应用
例2.7.2：以矩形薄板受单向拉伸力作用为例分析
圣维南原理及应用
通过圣维南原理的使用，可以将一些难以处理的边界
条件转化为基本方程所能够满足的边界条件，使得弹性力 学问题得到解答。
圣维南原理的推广：如果物体一小部分边界上的面
力是一个平衡力系（主失量和主矩都等于零），那么，这 个面力就只会使近处产生显著的应力，而远处的应力可以 不计。这是因为主失量和主矩都等于零的面力，与无面力 状态是静力等效的，只能在近处产生显著的应力。

弹性力学2详细讲解


C
cos
cos
sin
sin sin cos sin
cos
cos
sin
0
CCT
11
11 sin2
cos2
22
sin2
sin2
33
cos2
12 sin2 sin 2 23 sin 2 sin 31 sin 2 cos
22
11 cos2
cos2
22 cos2
17
力学与工程科学系
10
应变张量的柱坐标分量
cos sin 0
Cr
sin
cos
0
0
0 1
cos sin 0 11 12 13 cos sin 0
r
CrCrT
sin
cos
0
12
22
23
sin
cos
0
0
0 1 13 23 33 0
0 1
r 11
r 22
,x
y,zx
yz,x xy,z zx,y
,y
z,xy zx, y yz,x xy,z ,z
2020年11月25日
力学与工程科学系
14
Volterra积分
• 问题：上述必要条件是否充分？
0 u,使得： 1 u u？
2
• Volterra积分
ur u0 0 r r0
I1 J ii
I2
11 21
12 22 22 32
23 33 33 13
31 11
I3 det
2020年11月25日
力学与工程科学系
9
几何解释、变形椭球
• 体应变

弹性力学课件 第二章3


u = u0 −ωy v = v0 −ωx
4. 物理方程
平面应力问题
1 ε x = (σ x − µσ y ) E 1 ε y = (σ y − µσ x ) E 2(1+ µ) γ xy = τ xy E
1− µ 2 µ σ x − σy εx = E 1− µ
平面应变问题
这种等效只是从平衡的观点而言的，对刚体来而 言完全正确，但对变形体而言一般是不等效的。
2. 圣维南原理
如果把物体的一小部分边界上的面力，变换为分布 不同但静力等效的面力（主矢量相同，对同一点的主矩 也相同），那么，近处的应力分量将有显著的改变，但 远处所受的影响可以不计。
圣维南原理的说明： 1、圣维南原理只能应用于一小部分边界 （小边界，次要边界或局部边界）； 2、静力等效 ─ 指两者主矢量相同，对同一点 主矩也相同； 3、近处 ─ 指面力变换范围的一、二倍的局部 区域； 4、远处 ─ 指“近处 ”之外。
(b)
⑶ 它是在边界上物体保持连续性的条 件，或位移保持连续性的条件。
2. 应力边界条件 设在 Sσ 上给定面力分量 f x (s), f y (s) 在§2-3中，通过三角形微分体的平衡条件，导出坐 标面应力与斜面应力的关系式，
px = lσ x + mτ yx , py = mσ y + lτ xy
比较： 比较： 精确的应力边界条件 积分的应力边界条件 方程个数 方程性质 精确性 适用边界 2 3
函数方程（难满足） 代数方程（易满足） 精确 大、小边界 近似 小边界
思考题 1、为什么在大边界（主要边界）上，不能应用 圣维南原理？ 2、试列出负x 面上积分的应力边界条件， 设有各 种面力作用，或面力的主矢量和主矩作用。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章 变分原理与能量原理2.1 功和能基本概念能量法是与静力学方法平行的一种方法，对许多问题的求解更为方便，也能解决一些其它方法难以解决的复杂问题。

静力平衡方程方法——————————能量法⇓ ⇓解题复杂，有时甚至得不到全部平衡方程 能解决很复杂问题（一） 外力功与应变能的一般表达式 1.常力(集中力)·直线运动 θcos S F W ⋅= 2.变力·曲线运动⎰⎰==SS Fds w W 0cos θδ3.变形体：⎰∆=δpd W （p 不是常力）（准静态，而非冲击，即非波） 对线弹性体(准静态)δk p =⎰⎰∆∆∆===0202k d k pd W δδδ∆=P W 21（图示） 4.广义力与广义位移 集中力偶M ，转角θ ⎰=θMd W*问：线弹性结构外力功的计算是否能运用叠加原理?答：不能。

因()n i P P P ,,,21Λ=∆。

W 是i P 的二次函数而不是线性函数。

（二） 试述实功与虚功之区别。

当结构发生变形时，作用于结构的外力会在相应的位移上作功。

这里可分为两种不同的情况： (1)外力在自身引起的位移上作功，这种功称为实功。

例如，解6—1图(a)所示简支梁上外力1P 在位移叫11w 上所作之功即为实功，如解6—1图(b)中的阴影面积1A 所示。

其中11w 为外力1P 引起的位移。

(2)外力在其它因素引起的位移上作功，这种功称为虚功。

例如，解6—1图(a)所示简支梁上外力1P 在位移12w 上所作之功即为虚功，如解6-I 图(b)中的阴影面积2A 所示其中12w 为外力2P 在外力1P 处引起的位移。

实功与虚功的区别在于：(1)作实功时，外力随位移而变，故实功为变力作功；作虚功时，外力不随位移而变，故虚功为常力作功。

(2)作实功时，外力与自身引起的位移在方向上总是一致的，所以实功恒为正功；作虚功时，其它因素引起的位移与外力的方向就不一定一致了，所以虚功可正、可负。

以上仅就外力功作了讨论，至于内力实功与虚功的区别，请读者、自己思考。

（三） 弹性杆应变能的一般表达式()()()θϕδd x M d x T d x N dW dU 212121++== ()()()EIdxx M GI dx x T EA dx x N p 222222++=(忽略剪力，广义力乘广义位移) 在小变形条件下，变形与()x N ，()x T ，()x M 不耦合，可以叠加。

()()()⎰⎰⎰++=l l pl dx EI x M dx GI x T dx EA x N U 222222对于斜弯曲，弯矩沿主形心轴分解,()⎰l dx EI x M 22换成()()⎰⎰+l z z l y y dx EI x M dx EI x M 2222例：计算外力功：EIMl y EIPl y M A P A 2323==EIMl EIPl M A P A==θθ22单独作用P ：EIl P EI Pl P W P6321323=⋅=单独作用M ：EIl M EI Ml M WM2212=⋅= P 和M 共同作用：()()MAP A M A P A M P M y y P W θθ+++=+2121 EIlM EI PMl EI PMl EI Pl 24462223+++= 附加项*问：前述弹性杆应变能的一般表达式中各项是否能用叠加原理？ 答：能。

因各广义力引起的变形不耦合。

（四） 应变能和余应变能结构元件受到逐渐增大的载荷P 的作用，如图2-5所示。

当元件因受载而伸长时，载荷P 就作功。

在静力学中，由于不考虑惯性力(质量力)，所以，假设载荷的施加是非常缓慢的，同时在加载过程中没有热量的产生和消散，于是按照能量守恒原理，可知载荷所作的功W=结构变形所贮存应变能U对于具有非线性弹性特征的元件，典型的载荷一位移曲线如图2-6所示。

U dx e A Pdu W Lxx xx u===⎰⎰0σ式中：A ——元件的横截面积；L ——元件长度；应变dx du e xx /=。

图2-7中曲线下面的面积表示了应变能U 的大小。

⎰⎰-=PuudP Pu Pdu 0曲线上面的那部分面积用*U 表示，称为余应变能。

⎰⎰=-=PuudP Pdu Pu U 0*余应变能并无物理意义，它不过纯粹是为了使用上的方便而定义的一个数学量而已。

显然，u dPdU P dudU==*, 从图2-7也可以清楚地看出，在线弹性情况下，曲线退化为直线，U 与*U 相等，应变能和余应变能是完全可以互换的。

实际上，式（2-41)中的dU/dP ＝u 就是大家所熟知的卡氏第一定理，它只适用于线弹性(n ＝1)情况。

正确的关系式应该是u dP dU =/*，它无论在线弹性或非线性弹性情况下都是适用的。

（五） 位移函数表示的梁弯曲变形应变能1.中性层曲率表示的弯曲变形公式()EIx M =ρ1(其中M 可以通过弯矩方程表示为x 的函数，ρ为曲率半径，它可由y '和y ''表示) 2.由数学()23211y y '+''±=ρ3.挠曲轴微分方程()()EIx M y y ='+''±2321 (1) 4.方程简化，挠曲轴近似微分方程Θ小变形，()<≈'θy 0.0175(弧度)12<<'y112≈'+y ((1)式分母不再存在)()EIx My =''∴ 于是()()()()dx x x w EJ dx y EJ y d EIy d x M dU 22222''2'''2121⎪⎪⎭⎫ ⎝⎛∂∂====θ 2.2 变分原理举一个简单的例子，设有一安放在弹性地基上的梁，承受横向分布载荷q(x)的作用。

已知梁的一端(x=0)是固定的，另一端(x=L)是自由的。

问：梁取怎样的挠度w(x)才能使这个系统(系统是指梁、地基和载荷的总和)的总势能∏取最小值?系统总势能=梁弯曲应变能+地基变形能+载荷势能具体地，梁弯曲应变能b ∏：()⎰⎥⎦⎤⎢⎣⎡=∏Lb dx dx x w d EI 022221其中，EJ-----梁的弯曲刚度为，E----材料的弹性模量，J----主惯性矩地基中由于梁的挠度而贮存的能量f ∏为()[]⎰=∏Lf dx x w k 0221其中，κ-------弹性地基的刚度由于梁的挠度，载荷随之下降而使载荷的势能有了变化。

载荷势能q ∏的变化可以写成()()⎰=∏Lq dx x w x q 0现在，系统的总势能∏(即上列3者之和)为()()[]()()⎰⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-+⎥⎦⎤⎢⎣⎡=∏Ldx x w x q x w k dx x w d EI 022222121 此时，上述力学问题已经转化为如下数学问题：[]L x ,0∈，求w （x ），使它满足边界条件：()00=w ，()00'=w ，并上述积分定义的泛函∏取最小值显然，∏依赖于()x w 的变化，不同()x w 对应不同∏，此时，()x w 称为自变函数，∏则称为泛函。

(1)能够满足边界条件()00=w ，()00'=w 的自变函数()x w 可以有无穷多个，但同时满足使泛函∏取最小值的()x w 却只有一个，记为()x w *。

“相当于条条道路通罗马，但只有一条最近”。

(2)设在()x w *的附近有另一曲线()x w ，并令()()()x w x w x w δ+=*，如果)(x w δ足够小，是一无穷小量，则称)(x w δ是自变函数()x w 的变分。

)(x dw 和变分)(x w δ有本质上的差异。

)(x dw 是由于自变量x 的变化dx 引起，而)(x w δ则是自变量x 不变，函数()x w 本身的微小变化，可理解为()x w 函数形式作了微小变化，所以对于泛函∏来说，)(x w δ是自变函数()x w 的小变化。

以上问题在数学上可归纳为变分法问题：求泛函()()()[]⎰=∏ldx x w x w x w x F 0'',',,满足()00=w ，()00'=w 边界条件下的极小值所对应函数()x w 。

（一） 定积分dx y y x F ba⎰'),,(的驻立值问题给定问题：求()x y ，[]b a x ,∈，使它满足边界条件：（1）()()βα==b y a y ,；（2）泛函[]⎰=badxy y x F I ',,取极值。

分析过程：假定曲线GACH 就是所求的曲线()x y （如图2-1所示），则在其邻近的曲线GBDH 所对应的函数为)()(x y x y δ+（如图2-2所示），其中)(x y δ是一无穷小量（称为自变函数的变分，它使I 产生的增量I ∆）。

于是，相应于这两条曲线，可以求得()[]⎰++=∆+badx y y y y x F I I '',,δδ （2-1）图2-1由于()''y y δδ=（2-2）即微分运算与变分运算可互换（见书第3页），则I I ∆+可以写成[]⎰++=∆+badx y y y y x F I I '',,δδ（2-3）或者()()[]⎰-++=∆badx y y x F y y y y x F I ',,'',,δδ（2-4）由于被积函数F 是',,y y x 的连续可导函数，当y 'δ，y ''δ是无穷小量时，I ∆也是无穷小量，所以由泰勒级数公式：()())(''',,'',,高阶小量++⎪⎪⎭⎫⎝⎛∂∂+∂∂+=++Λy y F y y F y y x F y y y y x F δδδδ 略去高阶小量，则有⎰⎥⎦⎤⎢⎣⎡∂∂+∂∂=ba dx y y F y y F I ''δδδ（2-5)式中：I δ称做I 的一阶变分，简称变分，它是泛函增量中的一阶小量部分。

令y v y F u δ=∂∂=,'利用分部积分[]ba bab auv vdx u dx uv +-=⎰⎰''（2-6)则式（2-5)的右端第2项可改写为ba bab a y y F ydx y F dx d dx y y F ⎥⎦⎤⎢⎣⎡∂∂+⎪⎪⎭⎫⎝⎛∂∂-=∂∂⎰⎰δδδ'''' （2-7)将式（2-7)代入式（2-5)，得ba ba y y F ydx y F dx d y F I ⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=⎰δδδ'' （2-8)由边界条件a x =和b x =处，0=y δ,故式（2-8)最后一项必等于零。