绘制函数曲线
- 格式:pdf
- 大小:241.53 KB
- 文档页数:12

excel曲线函数
Excel中的曲线函数可以帮助我们通过已知的数据绘制出一条平
滑的曲线。
其中最常用的曲线函数是平滑曲线函数和散点图曲线函数。
平滑曲线函数是指通过一系列的数据点,利用二次函数或三次函
数的形式进行拟合,从而得到一条平滑的曲线。
该函数常用于连续变
量的分析,例如时间或温度等。
散点图曲线函数则是将散点图转换为平滑曲线函数。
该函数常用
于非连续变量的拟合,例如多个观察值之间的关系。
在Excel中,我们可以通过插入图表来创建曲线函数。
选择所需
的数据范围后,在插入图表中选择对应的曲线类型即可完成曲线函数
的绘制。

本文整理于网络,仅供阅读参考
excel画出函数曲线的教程
excel画出函数曲线的教程:
画出函数曲线步骤1:首先我们新建一个excel图表。
画出函数曲线步骤2:我们取a列为自变量x,b列为因变量y。
首先我们在a列输入自变量x的范围。
画出函数曲线步骤3:接下来是编辑公式。
我们的函数式是y=2x^2+4。
点住b1这个表格,在红圈处输入函数公式。
需要注意的是我们不能直接输入y=2x^2+4,而是输入=abs(((a1)^2*2)+4),这是公式的固定格式,必须严格遵守。
其中需要注意的是,这比较类似向计算器中输入计算式,括号和运算符号是不能省略的,另外自变量x用a1代替。
输入之后点回车键,就计算出来了。
画出函数曲线步骤4:点住图中所示的光标向下拉,就将因变量y定义域中的值计算出来了。
画出函数曲线步骤5:在工具栏中选择:插入-图表-折线图。
子图表可以选择自己需要的。
点击“完成”,即得到所需的函数图像。
看了excel画出函数曲线的教程。

excel如何制作动态正余弦函数曲线图像
1、首先启动excel2003,我们都清楚正余弦函数的表达式为
x1=A*sin(θ+φ)和x2=A*cos(θ+φ),通过改变A和φ的值改变
函数的状态。
2、选择单元格a3输入x,从单元格a4开始一直到单元格a40
填充内容为0、10、20-360等差数列。
4、同样道理在单元格c3中输入cos函数,选择单元格c4输入
公式为=$f$3*sin(radians(a4+$h$3)),然后填充其他数值。
6、这样就得到了正余弦函数图像,选择单元格d18,执行视图-
工具栏-窗体命令,调出窗体对话框,选择微调器,绘制一个微调器。
并调节其大小和位置。
7、右键单击该微调器从下拉菜单中选择设置控件格式选项,调
出设置控件格式对话框,设置最小值为1,最大值为6,步长为1,
单元格连接为$f$2,当前值为6,点击确定。
8、接着在单元格d19中绘制一个微调器同样方法设置当前值为0,最小值为0,最大值为360,步长为10,单元格链接地址为h2.
点击确定按钮。
9、像制作正弦函数那样制作余弦函数的微调器,并进行相应的
参数设置,设置完毕后可以查看效果。
10、调整图表所在的位置,使其和微调器在一条线,这样再调节数据时能够清楚的看出图像的变化。
12、双击图表中的函数图像打开数据系列格式对话框,在该对话框中分别设置正余弦函数图像的样式和颜色,然后点击确定按钮。
13、到此就基本上完成了,点击任意一个微调器动态观看函数图像变换,执行文件-保存命令,在弹出的对话框中输入“动态变化图像”,找到一个合适的位置保存即可。
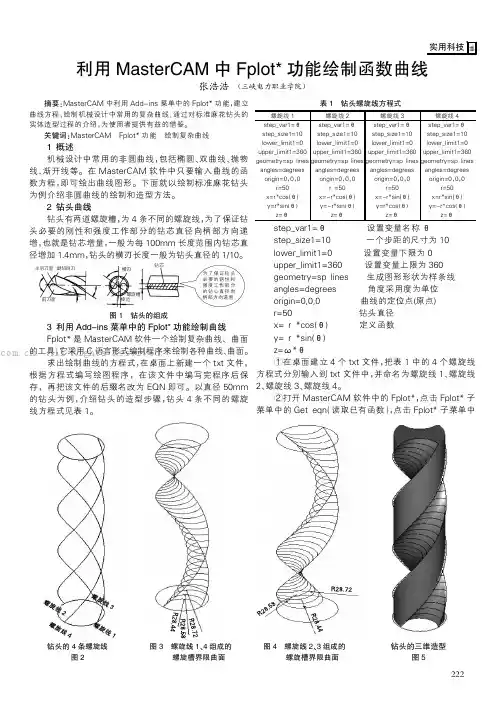
图3螺旋线1、4组成的螺旋槽界限曲面摘要:MasterCAM 中利用Add-ins 菜单中的Fplot*功能,建立曲线方程,绘制机械设计中常用的复杂曲线;通过对标准麻花钻头的实体造型过程的介绍,为使用者提供有益的借鉴。
关键词:MasterCAM Fplot*功能绘制复杂曲线1概述机械设计中常用的非圆曲线,包括椭圆、双曲线、抛物线、渐开线等。
在MasterCAM 软件中只要输入曲线的函数方程,即可绘出曲线图形。
下面就以绘制标准麻花钻头为例介绍非圆曲线的绘制和造型方法。
2钻头曲线钻头有两道螺旋槽,为4条不同的螺旋线,为了保证钻头必要的刚性和强度工作部分的钻芯直径向柄部方向递增,也就是钻芯增量,一般为每100mm 长度范围内钻芯直径增加1.4mm,钻头的横刃长度一般为钻头直径的1/10。
为了保证钻头必要的钢性和强度工作部分的钻心直径向柄部方向递增钻芯棱边螺旋槽横刃前刀面主后刀面副切削刀图1钻头的组成3利用Add-ins 菜单中的Fplot*功能绘制曲线Fplot*是MasterCAM 软件一个绘制复杂曲线、曲面的工具,它采用C 语言形式编制程序来绘制各种曲线、曲面。
求出绘制曲线的方程式,在桌面上新建一个txt 文件,根据方程式编写绘图程序,在该文件中编写完程序后保存,再把该文件的后缀名改为EQN 即可。
以直径50mm的钻头为例,介绍钻头的造型步骤,钻头4条不同的螺旋线方程式见表1。
step_var1=θ设置变量名称θstep_size1=10一个步距的尺寸为10lower_limit1=0设置变量下限为0upper_limit1=360设置变量上限为360geometry=sp lines 生成图形形状为样条线angles=degrees 角度采用度为单位origin=0,0,0曲线的定位点(原点)r=50钻头直径x=r *cos(θ)定义函数y=r *sin(θ)z=ω*θ①在桌面建立4个txt 文件,把表1中的4个螺旋线方程式分别输入到txt 文件中,并命名为螺旋线1、螺旋线2、螺旋线3、螺旋线4。

turtle画二次函数曲线
在Python中,我们可以使用turtle库来绘制二次函数曲线。
以下是一个简单的例子,它绘制了一个二次函数y = x^2的图形:
python复制代码:
import turtle
# 创建一个新的turtle screen,并设置其背景色为白色
screen = turtle.Screen()
screen.bgcolor("white")
# 创建一个新的turtle对象
my_turtle = turtle.Turtle()
# 设置画笔的速度
my_turtle.speed(1)
# 循环绘制二次函数y = x^2的图形
for x in range(-200, 200):
y = x**2
my_turtle.penup()
my_turtle.goto(x, -y) # 移动到下一个点的位置
my_turtle.pendown()
my_turtle.forward(2) # 绘制一个短的线段
# 关闭turtle graphics window
turtle.done()
这个程序将会绘制一个二次函数y = x^2的图形。
你可以通过改变循环的范围和步长来改变图形的精度和范围。
你也可以通过改变forward函数的参数来改变线段的长度。

数学中的函数图像的绘制与应用在数学中,函数是一个非常重要的概念。
而函数图像则是对函数进行可视化的一种方式,它可以让我们更加直观地理解函数的特征和性质。
本文将探讨函数图像的绘制方法、常见的函数图像形态及其应用。
一、函数图像的绘制方法函数图像绘制是一种基于函数的可视化表示方法。
为了绘制函数图像,我们需要先确定要绘制的函数。
这样才能在坐标系内绘制出函数的图像。
下面将介绍如何在笛卡尔坐标系中绘制常见的函数图像。
1. 直线函数的图像绘制直线函数方程为y=kx+b(其中k、b为常数),其图像通常是一条斜率为k,截距为b的直线。
这里以y=2x+1为例,绘制其函数图像的步骤如下:(1)构建坐标系:在纸上画一个直角坐标系。
(2)确定坐标:通过设定变量的值进行逐一计算;或设置x轴和y轴的单位间隔,根据方程中的值确定函数图像上的点坐标。
(3)依据坐标绘图:在坐标系中依照前面计算出来的坐标,描绘出直线。
2. 幂函数的图像绘制幂函数的方程通常具有以下形式:y=x^n(其中n为常数)。
幂函数的图像形态与其幂指数的正负有关。
当幂指数为正数时,函数的图像呈现出向上的凸形状;当幂指数为负数时,函数的图像则呈现出向下的凹形状。
以y=x^2为例,绘制其函数图像的步骤如下:(1)构建坐标系:在纸上画一个直角坐标系。
(2)确定坐标:通过设定变量的值进行逐一计算;或设置x轴和y轴的单位间隔,根据方程中的值确定函数图像上的点坐标。
(3)依据坐标绘图:在坐标系中依照计算出来的坐标,连结相邻的点形成一条曲线。
由于幂函数的曲线通常比较平滑,因此绘制时需要分段绘制(例如x<0部分,x=0的位置,x>0部分等),并且需要足够细致。
3. 三角函数的图像绘制三角函数具有周期性的特点,也就意味着可以将函数图像沿周期区间翻折并重叠,以此来推出整个函数图像的形态。
以下以正弦函数y=sin(x)为例,绘制其函数图像的步骤如下:(1)构建坐标系:在纸上画一个直角坐标系。

率失真函数曲线绘制
率失真函数是信息论中的一个重要概念,它描述了信源编码和信道编码中的失真与率之间的关系。
在信息论中,通常使用率失真函数来衡量信源编码和信道编码的性能。
率失真函数通常用R(D)表示,其中R表示编码率,D表示失真度量。
在绘制率失真函数的曲线时,我们需要首先选择一个合适的失真度量,比如均方误差或者信噪比。
然后,我们可以通过改变编码率来计算不同失真度量下的失真值,最终得到一组编码率和失真度量的数据点。
最后,我们可以使用这些数据点绘制出率失真函数的曲线。
在绘制率失真函数曲线时,我们可以从多个角度进行分析。
首先,我们可以观察曲线的斜率,斜率越大表示单位失真度量所需要的码率越高,这可以帮助我们理解编码的效率。
其次,我们可以观察曲线的凹凸性质,凹部分表示存在着最优的编码方案,这可以帮助我们选择最佳的编码率。
此外,我们还可以比较不同编码算法或者不同信道条件下的率失真函数曲线,从而评估它们的性能差异。
绘制率失真函数曲线需要使用数学工具和编程语言进行计算和可视化。
我们可以使用Python中的Matplotlib库或者MATLAB等工具来实现。
在代码中,我们需要定义失真度量的计算方法和不同编
码率下的编码器和解码器,然后计算出不同失真度量下的失真值,并绘制成曲线图表。
总之,绘制率失真函数曲线是信息论中的重要任务,它能够帮助我们理解编码和解码的性能,并且为我们选择合适的编码方案提供参考。
通过绘制曲线并从多个角度进行分析,我们可以更好地理解率失真函数的特性和应用。


怎样用Excel函数画曲线有时候工作需要我们电脑绘制复杂函数曲线,怎么做呢?对于新手来说还是有一定难度,怎么办?下面店铺给大家分享用Excel函数画曲线的方法。
用Excel函数画曲线的方法1.用Excel函数画曲线图的一般方法因为Excel有强大的计算功能,而且有数据填充柄这个有力的工具,所以,绘制曲线还是十分方便的。
用Excel画曲线的最大优点是不失真。
大体步骤是这样的:⑴ 用“开始”→“程序”→“Microsoft office”→”Excel”,以进入Excel窗口。
再考虑画曲线,为此:⑵ 在A1 和A2单元格输入自变量的两个最低取值,并用填充柄把其它取值自动填入;⑶ 在B列输入与A列自变量对应的数据或计算结果。
有三种方法输入:第一种方法是手工逐项输入的方法,这种方法适合无确定数字规律的数据:例如日产量或月销售量等;第二种方法是手工输入计算公式法:这种方法适合在Excel的函数中没有列入粘贴函数的情况,例如,计算Y=3X^2时,没有现成的函数可用,就必须自己键入公式后,再进行计算;第三种方法是利用Excel 中的函数的方法,因为在Excel中提供了大量的内部预定义的公式,包括常用函数、数学和三角函数、统计函数、财务函数、文本函数等等。
怎样用手工输入计算公式和怎样利用Excel的函数直接得出计算结果,下面将分别以例题的形式予以说明;⑷ 开始画曲线:同时选择A列和B列的数据→“插入”→“图表”→这时出现如下图所示的图表向导:选“XY散点图”→在“子图表类型”中选择如图所选择的曲线形式→再点击下面的‘按下不放可查看示例’钮,以查看曲线的形状→“下一步”→选“系列产生在列”→“下一步”→“标题”(输入本图表的名称)→“坐标”(是否默认或取消图中的X轴和Y轴数据)→“网络线”(决定是否要网格线)→“下一步”后,图形就完成了;⑸ 自定义绘图区格式:因为在Excel工作表上的曲线底色是灰色的,线条的类型(如连线、点线等)也不一定满足需要,为此,可右击这个图,选“绘图区格式”→“自定义”→“样式”(选择线条样式)→“颜色”(如果是准备将这个曲线用在Word上,应该选择白色)→“粗细”(选择线条的粗细)。

在PPT课件中动态绘制各类函数曲线作者:马致明来源:《电脑知识与技术》2011年第25期摘要:在探究PowerPoint VBA绘图方法的基础上,剖析如何利用VBA编程在PPT课件中直接绘制各类可控参数的静态和动态平面函数曲线,并给出了具体的制作实例。
关键词:VBA编程;静态曲线;动态曲线;绘制;PPT课件中图分类号:TP311文献标识码:A文章编号:1009-3044(2011)25-6232-03Dynamically Mapping Various Function Curve in PPT CoursewareMA Zhi-ming(College of Computer Science and Technology, Xinjiang Normal University, Urumqi 830054, China)Abstract: After studding PowerPoint VBA mapping method, it has been analyzed that how to mapping Various static and dynamic function curve by using VBA programming in PPT courseware. An example has been given also.Key words: VBA programming; static function curve; dynamic function curve; mapping; PPT coursewarePowerPoint由于简单易用等优点成为众多教师制作课件的首选工具,它所附带的编程工具VBA则给使用者提供了对演示文稿进行二次开发的环境,从而使演示文稿的功能更加强大。
函数曲线的绘制在数学、物理、电子等学科的课件中经常出现,特别是可控参数的交互式静态函数曲线和动态函数曲线的绘制更是体现课件制作水平高低的要素之一。

matlab曲线绘制函数一、概述MATLAB是一款强大的数学软件,它提供了丰富的绘图功能,可以方便地绘制各种函数曲线。
本文档将介绍如何使用MATLAB绘制曲线的基本步骤和常用函数。
二、基本步骤1. 导入数据:首先需要将需要绘制的函数数据导入MATLAB中,可以使用内置函数如load或data函数从文件中导入数据。
2. 创建函数句柄:使用内置函数如fun或expression创建函数句柄,该句柄将用于表示需要绘制的函数。
3. 创建绘图对象:使用内置函数如plot或hold on创建绘图对象,该对象将用于表示绘制曲线的位置和线条样式。
4. 添加标题和标签:使用内置函数如title或xlabel添加标题和坐标轴标签。
5. 保存图像:使用saveas或print函数将图像保存到本地文件或在线展示。
三、常用函数1. plot函数:用于绘制单条曲线,可以指定线条颜色、线型和线条宽度等参数。
2. hold on函数:用于在绘图区域中连续绘制多条曲线,当前绘制的曲线将在后面绘制的曲线覆盖上。
3. plotyy函数:用于在同一图中绘制两条垂直曲线,适合绘制一对互为函数的曲线。
4. legend函数:用于添加图例,以说明每条曲线的名称和对应的数据变量。
5. xlabel和ylabel函数:用于添加坐标轴标签,以便更好地描述曲线的坐标轴范围和单位。
6. title函数:用于添加图像标题,以便更好地概括图像的主题和内容。
7. meshgrid函数:用于生成网格坐标,可以方便地计算多个坐标点的数值和点集。
四、示例代码及图像展示下面是一个简单的示例代码,用于绘制正弦曲线和余弦曲线的图像。
代码中使用了MATLAB内置的sin和cos函数,以及plot函数绘制曲线。
```matlab% 导入数据x = -pi:0.1:pi; % 定义x轴范围y_sin = sin(x); % 计算正弦值y_cos = cos(x); % 计算余弦值% 创建绘图对象并绘制曲线figure; % 创建新图像窗口plot(x, y_sin); % 绘制正弦曲线hold on; % 在当前绘图区域中继续绘制曲线plot(x, y_cos); % 绘制余弦曲线hold off; % 移除前面绘制的覆盖层,使后续曲线可见% 添加标题和标签title('正弦余弦曲线比较'); % 添加图像标题xlabel('x轴'); % 添加x轴标签ylabel('y值'); % 添加y轴标签legend('sin', 'cos'); % 添加图例,说明每条曲线的名称和对应的数据变量```运行上述代码后,将得到一幅包含正弦曲线和余弦曲线的图像,如图所示:(请在此处插入图像)通过上述示例代码和图像展示,我们可以看到MATLAB绘制曲线的基本步骤和常用函数的用法。
函数图像:绘制函数图像函数图像是在数学中常见的一种图形表示方式,能够直观地展示出函数的性质和变化规律。
接下来,我们将探讨函数图像的绘制方法以及函数图像在数学中的应用。
一、函数图像的绘制方法函数图像的绘制是通过给定函数的输入值,计算出对应的输出值,并将这些点连线而成的曲线。
具体的绘制方法如下:1. 确定函数的定义域和值域:在绘制函数图像之前,我们首先需要确定函数的定义域(输入值的范围)和值域(输出值的范围),这有助于我们确定绘制图像的范围和比例。
2. 选择合适的坐标系:函数图像的绘制需要借助坐标系来进行,一般我们采用直角坐标系,即x轴和y轴互相垂直。
在确定合适的坐标系后,我们可以将坐标系按照定义域和值域的范围进行调整,以便将函数图像完整地展示出来。
3. 计算关键点的坐标:在绘制函数图像时,我们需要选择一些关键点来确定曲线的形状和走向。
一般而言,我们可以选择定义域中的几个特殊点,如零点、极值点、拐点等,计算它们在坐标系中的具体位置。
4. 连接关键点绘制曲线:在计算完关键点的坐标后,我们可以使用直线或曲线将这些点依次连接起来,形成函数的图像。
在绘制曲线时,需要注意连线的平滑性和曲线的走向,以便更好地展示函数的变化规律。
二、函数图像在数学中的应用函数图像在数学中具有重要的应用价值,可以帮助我们更好地理解和分析各种函数的性质和特点。
以下是函数图像应用的几个方面:1. 函数的可视化分析:函数图像可以直观地展示函数的变化规律,帮助我们分析函数的特点,如增减性、奇偶性、周期性等。
通过观察函数的图像,我们可以更好地理解函数的行为,并在解决实际问题时提供参考。
2. 函数的极值点和拐点:通过绘制函数的图像,我们可以确定函数的极值点和拐点的位置。
极值点是函数在特定区间内取得最大值或最小值的点,而拐点是函数曲线由凹转凸或由凸转凹的点。
这些点的位置可以通过函数图像的特点和走向来确定,有助于我们进一步分析函数的变化规律。
3. 函数的图像变换:函数图像可以通过一系列变换(如平移、伸缩、翻转等)来改变形状和位置。
实验一 绘制函数曲线1.本次实验的目的和要求掌握、理解熵函数、平均互信息量的表达式及其性质2.实验内容或原理1)绘制二进制熵函数图像12,()1X x x P x p p ⎧⎡⎤⎫=⎨⎬⎢⎥-⎣⎦⎭⎩ 01p ≤≤ (,1)log (1)log(1)H p p p p p p -=----2)绘制三进制熵函数图像12312121()x x x X p p p p P x ⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦ 121211221212(,,1)log log (1)log(1)H p p p p p p p p p p p p --=-------3)绘制平均互信息量图形,,(;)()(/)(/)(,)log ()(,)(;)k j k j k j k k j k j k jI X Y H X H X Y p x y p x y p x p x y I x y =-⎡⎤=⎢⎥⎣⎦=∑∑ 3. 例:绘制二进制熵函数图像P=0.00001:0.001:1..*log2()(1)*log2(1);h p p p p =----plot(p,h);title(‘二进制熵函数曲线’);ylable(‘H(p ,1-p)’)4.实验报告要求交纸质实验报告,要求有源程序,函数图象。
1)绘制二进制熵函数图像p=0.00001:0.01:1h=-p.*log2(p)-(1-p).*log(1-p);plot(p,h);title('二进制熵函数曲线');ylabel('H(p,1-p)');2)绘制三进制熵函数图像p1=0.00001:0.01:1p2=0.00001:0.001:1[p1,p2]=meshgrid(p1,p2);h=-p1.*log2(p1)-p2.*log2(p2)-(1-p1-p2).*log(1-p1-p2);plot3(p1,p2,h);title('三进制熵函数曲线');ylabel('H(p1,p2,1-p1-p2)');grid;3)绘制平均互信息量图形p=0.00001:0.01:1[x,p]=meshgrid(p);y=x+p-2*x.*p;Hy=-y.*log2(y)-(1-y).*log2(1-y);Hp=-p.*log2(p)-(1-p).*log2(1-p);I=Hy-Hp;plot3(x,p,I);title('平均互信息量图像');xlabel('x');ylabel('p');ylabel('I');grid;5.思考题1)你能从二进熵函数的图形中了解它的一些什么性质?答:对称性,非负性,上凸性2)怎样绘制各种单位的二进熵函数图形?附着log函数的底的增加,二进熵函数的图形是如何变化的?3)如何编写一个计算一般的熵函数的程序?。
【主题】gglpot函数绘制roc曲线一、概述在统计学和机器学习中,ROC曲线是一种常用的评估分类模型性能的工具。
它可以帮助我们理解模型的准确性和灵敏性,并且能够有效地比较不同模型的表现。
而ggplot函数,则是R语言中强大的绘图工具,可以用来绘制各种数据可视化图表。
本文将重点介绍如何使用ggplot 函数来绘制ROC曲线,以及对ROC曲线的理解和分析。
二、ROC曲线简介ROC曲线全称为“受试者工作特征曲线”(Receiver Operating Characteristic curve),它是一种用于描述二元分类模型表现的图表。
ROC曲线的横轴是“假阳性率”(False Positive Rate,FPR),纵轴是“真阳性率”(True Positive Rate,TPR)。
在理想情况下,ROC曲线会沿着左上角缓慢上升,然后向右上方水平延伸。
ROC曲线下方的面积(AUC)被用来衡量模型的性能,AUC值越大,模型的性能越好。
三、ggplot函数绘制ROC曲线使用ggplot函数绘制ROC曲线需要借助一些额外的包,比如“pROC”和“ggplot2”。
我们需要用pROC包计算模型的预测概率和真实标签,得到ROC曲线的数据。
将得到的ROC曲线数据作为ggplot函数的输入,使用geom_path()函数来绘制ROC曲线图表。
另外,我们还可以通过添加主题、标签和注释等方式,使得ROC曲线图表更加美观和易于理解。
四、对ROC曲线的分析与理解在分析ROC曲线时,我们需要关注曲线是否靠近左上角以及AUC的数值。
如果ROC曲线很接近左上角,说明模型具有较高的准确性和灵敏性;而AUC值越接近1,说明模型的性能越好。
我们还可以根据ROC曲线的形状,来判断模型的优劣和对比不同模型的性能差异。
在实际应用中,我们可以根据 ROC 曲线的形状和 AUC 值来选择最适合的模型,并据此进行进一步的改进和优化。
五、个人观点和理解对于ROC曲线的绘制和分析,我个人认为它是评估分类模型性能的重要工具之一。
互相关函数曲线的绘制实验数据本次实验旨在研究互相关函数曲线的绘制过程,通过该实验,我们可以更加深入地了解互相关函数曲线的原理和特点,为下一步的相关研究提供有力的支持。
首先,我们需要准备实验所需的材料和仪器,包括计算机、MATLAB软件、数据采集器、信号发生器和示波器等。
接着,我们将进行以下实验步骤:1. 准备两个信号的原始数据,并将其通过信号发生器输入到数据采集器中进行采集。
本次实验中,我们选择的两个信号分别为正弦波和方波信号,频率分别为10Hz和20Hz。
2. 将采集到的两个信号数据导入MATLAB软件中,通过MATLAB的函数库进行信号处理和分析。
首先,我们需要通过FFT算法将信号数据转换为频域数据,然后使用相关函数计算两个信号的互相关函数。
通过互相关函数的计算,我们可以获得两个信号之间的相似程度和时间延迟。
3. 绘制互相关函数曲线。
在绘制互相关函数曲线时,我们需要确定X轴和Y轴的坐标范围,并选择合适的线性或对数坐标系。
在本次实验中,我们选择使用线性坐标系,X轴表示时间延迟,Y轴表示互相关函数值。
通过绘图,我们可以直观地观察到两个信号之间的相关情况。
4. 进行数据分析和结果验证。
在实验过程中,我们需要对绘制的互相关函数曲线进行数据分析和结果验证,以确定实验结果的可信性和准确性。
如果发现数据异常或结果不一致,需要重新检查实验过程和数据处理方法,排除可能出现的误差因素。
通过以上实验步骤,我们可以成功绘制互相关函数曲线,并获得两个信号之间的相关程度和时间延迟。
在实验数据分析中,我们发现正弦波和方波信号的互相关函数曲线具有不同的特点,其互相关函数值的变化趋势和峰值位置也存在显著差异。
这表明互相关函数曲线在不同类型信号之间具有较好的区分性和可解释性,为信号处理和分析提供了有力的工具。
总之,本次实验为我们深入了解互相关函数曲线的绘制过程和分析方法提供了重要的实践机会,为以后的相关研究奠定了基础。
同时,我们还需要进一步探索互相关函数曲线在不同应用场景下的应用和发展,以提高其在实际应用中的效果和效率。
excel怎么绘制函数曲线
excel是日常办公必不可少的工具之一,其有很强大的功能,那么今天小编就教教大家怎么绘制一条函数曲线吧。
excel绘制函数曲线的步骤:
1) 自变量的输入
在某张空白的工作表中,先输入函数的自变量:在A列的A1格输入“X=”,表明这是自变量。
再在A列的A2及以后的格内逐次从小到大输入自变量的各个值;实际输入的时候,通常应用等差数列输入法,先输入前二个值,定出自变量中数与数之间的步长,然后选中A2和A3两个单元格,使这二项变成一个带黑色边框的矩形,再用鼠标指向这黑色矩形的右下角的小方块“■”,当光标变成“+”字型后,按住鼠标拖动光标到适当的位置,就完成自变量的输入。
2) 输入函数式
在B列的B1格输入函数式的一般书面表达形式,y=|lg(6+x^3)|。
在B2格输入“=ABS(LOG10(6+A2^3))”,B2格内马上得出了计算的结果。
这时,再选中B2格,让光标指向B2矩形右下角的“■”,当光标变成“+”时按住光标沿B列拖动到适当的位置即完成函数值的计算。
3) 绘制曲线
点击工具栏上的“图表向导”按钮
,选择“X,Y散点图”,然后在出现的“X,Y散点图”类型中选择“无数据点平滑线散点图”。
此时可察看即将绘制的函数图像,发现并不是我们所要的函数曲线。
单击“下一步”按钮,选中“数据产生在列”项,给出数据区域。
单击“下一步”按钮。
单击“下一步”按钮,单击“完成”按钮。
这时曲线就在我们面前了。
AutoCAD 中绘制函数曲线的若干方法AutoCAD 本身没有提供函数曲线的绘制功能,但我们可以通过多种方法来实现函数曲线的绘制:1. 1. 借助另外的能绘制函数曲线的借助另外的能绘制函数曲线的CAD 软件,如CAXA CAXA。
CAXA 提供了丰富的函数曲线,并可自定义。
在CAXA 中绘制好曲线后,保存为dwg 文件,再在AutoCAD 中打开,复制到你的图形文件中。
2. 2. 借助借助Excel Excel,在,在Excel 中把函数的若干点坐标计算出来,再合并成点对后在AutoCAD 中用样条曲线来绘制这些点对。
以楼主说的正弦曲线为例说明如下:(1)在Excel 的A 列中输入函数自变量的若干值(可以用自动填充功能),并在B 例用公式计算出函数值。
如A1中输入“中输入“--180“,A2中输入“=中输入“=A1A1A1+1”。
+1”。
在B1中输入“=40*SIN(PI()*A1/180)“,其中40是振幅,把正弦曲线的Y 方向变化幅度增强(可根据对曲线的变化幅度的要求给其他值),PI ()*A1/180是将A1单元格的数据转换为弧度。
再拖运复制B1单元格的数据到B2B2。
(2)在C1单元格中输入:=单元格中输入:=A1&","&B1A1&","&B1A1&","&B1,把,把A1和B1中的数据组成一对坐标点对,相当于A1是X 轴坐标,轴坐标,B1B1是Y 轴坐标。
并把公式复制到C2C2。
(3)选择A2A2::C2两个单元格,向下拖运复制到A361A361::C261C261(角度从(角度从(角度从--180°到+180°)。
在C1C1::C361中得到一个函数周期的坐标点对数据。
(4)选择C1C1::C361C361,并复制。
,并复制。
(5)在AutoCAD 中输入命令:中输入命令:SPLINE SPLINE SPLINE(或绘图——样条曲线),这时命令(或绘图——样条曲线),这时命令提示:指定第一个点或提示:指定第一个点或 [ [ [对象对象对象(O)]: (O)]:此时,把鼠标定位到提示行的最后,即那个冒号(:)后面,按Ctrl+V Ctrl+V。