当前位置：文档之家 › 非理想流动模型

非理想流动模型

  • 格式：pptx
  • 大小：782.56 KB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

第四章-停留时间分布

第四章-停留时间分布


可见，F（t）与C（t）有相同的变化趋势，二者仅差常数C0。
3.脉冲法测定E( t )
0，t < 0
V0
示 踪
剂M
反应器
VR
检测器
C( t )
V0
注入刺激浓度 C = C0，t = 0 0，t > 0
C0
脉冲刺激
C0
应答曲线
Δt Δt
0
t
0
t
示踪剂物料衡算式，在dt 时间内， V0
排出量为V0C(t)dt，总量为
整理得
dC(t) dt
V0 VR
[C0
C(t)]
1 tm
[C0
C(t)];
或
dC(t) dt ; C0 C(t) tm
积分得 F (t) C(t) 1 et tm ; E(t) dF (t) 1 et tm
C0
dt tm
F( t ) E( t )
1.0
1 et tm
0
t
1 et tm
1
tm
示
M 0 V0C(t)dt
踪
剂M
反应器
VR
检测器
C( t )
V0
于是 1 V0 C(t)dt, 与归一化式
E(t)dt 1
比较，得
0M
0
E(t) V0 C(t) ( 停留时间分布密度函数公式） M
在实际实验中，脉冲注入示踪剂的量可从实验数据中求得：
M V0 0 C(t)dt,
停留时间分布密度可写成： E(t) 因停留时间分布函数为
时间t （s） 0 120 240 360 480 600 720 840 960 1080
示踪剂浓度 0 6.5 12.5 12.5 10.0 5.0 2.5 1.0 0.0 0.0 C（g / m3)
第二章 理想流动与非理想流动1

第二章 理想流动与非理想流动1

第二章
理想流动与非理想 流动反应器
流体在反应器中的流动情况影响着反应速率、反应选择率， 直接影响反应结果，研究反应器的流动模型是反应器选型、设计 和优化的基础。 流动模型可以抽象出两种极限的情况：一种是完全没有返混 的活塞流反应器；另一种是返混达到极大值的全混流反应器。 实际生产中的多数管式反应器及固定床催化反应器等可作活 塞流反应器处理，多数槽式反应器可作全混流反应器处理。
对活塞流反应器，物料质点是平推着向前流动的，物料质点在反 应器中的逗留时间相同不产生返混。而在全混流反应器中，不同 年龄的质点达到完全混合，有的逗留时间很短，有的却很长，返 混程度最大。 活塞流与全混流是两种理想流型：前者理想置换，没有返混；后 者理想混合，返混最大。而介于两者之间的流型，是非理想流型， 存在着不同程度的返混现象。
2 全混流模型 亦称理想混合模型或连续搅拌槽式反应器模型，如图2-1（c）所 示，是一种返混程度为无穷大的理想化流动模型。
全混流假定反应物料以稳定流率流入反应器，在反应器中，刚进 入反应器的新鲜物料与存留在器内的物料在瞬间达到完全混合。 反应器中所有空间位置的物料参数都是均匀的，等于反应器出口 处的物料性质，即反应器内物料温度、浓度均匀，与出口处物料 温度、浓度相等。而物料质点在反应器中的逗留时间参差不齐， 有的很短，有的很长，形成一个逗留时间分布。 搅拌十分强烈的连续搅拌槽式反应器中的流体流动可视为全混流。
（2）热量衡算 热量衡算以能量守恒与转化定律为基础，在计算反应速率时必须 考虑反应物系的温度，通过热量衡算可以计算反应器中温度的变 化。与物料衡算相仿，对反应器或其一微元体积进行反应物料的 热量衡算，基本式为 （带入的热焓）＝（流出的热焓）十（反应热）十（热量的 累积）十（传向环境的热量） （2-2） 式中反应热项，放热反应时为负值，吸热反应时为正值。
化学反应工程第三章反应器内的流体流动

化学反应工程第三章反应器内的流体流动


物料的浓度变化。
如测定数据属于离散型， 则：
3.2.3 寻求停留时间分布的实验方法
在实验时，时间间隔可以取成等值，得：
平均停留时间和散度可按下式计算：
当 为定值时，
散度
3.2.3 寻求停留时间分布的实验方法
例3-2 在稳定操作的连续搅拌式反应器的进料中脉冲
m 50g
注入染料液（
）,测出出口液中示踪剂浓度随时
多级混合模型是由N个容积为V的全混釜串联组成，从一 个釜到下一个釜的管道内无返混且不发生化学反应，示 意如图3-8：
图3-8 多级混合模型
3.4.1 多级混合模型
经推导可得该多级混合模型的停留时间分布规律为：
F ( ) cN 1 1 1 1 1 exp( N )[1 ( N ) ( N ) 2 ( N ) 3 （N ) N 1 ] c0 1 ！ 2 ！ 3! （N 1 ）！
（t）；另一部分是阶跃输入前的物料量为Vc0－中时间
大于t的示踪剂，其量为Vc0－[1-F（t）] 。即：
即得：
（3-15）
如果阶跃输入前进口物料中不含示踪剂，即 ，则上 c F ( t ) 式可以改写成： （3-16） c0
3.2.3 寻求停留时间分布的实验方法
例3-1 测定某一反应器停留时间分布规律，采用阶跃输 入法，输入的示踪剂浓度 ，在出口处测定响应曲线得到 的数据如下表3-1所示：
占的分率。依此定义，E(t)和F(t)之间应具有如下关
系： 以及
3.2.1 停留时间分布的定量描述
在t=0时 F(0)=0和t=∞时 ，关于E(t)、F(t)曲线以及它 们之间的关系示于图3-2中。
图3—2 停留时间分布曲线
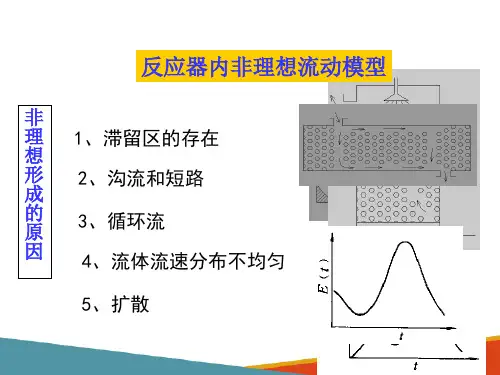
反应器基础知识—流体流动

反应器基础知识—流体流动


改善措施
1、增大流体在设备内的湍流程度，以消除轴向扩散而造
非 理
成的停留时间分布不均匀的现象。
想 2、在反应器内装设填充物，以改变设备内速度分布和浓
流 动
度分布，从而使停留时间分布趋于均一化。但要注意避免
的 沟流和短路现象的发生。

改
善 3、增加设备级数或在设备内增设挡板。
4、采用适当的气体分布装置，或调节各组反应管的阻力，
停留时间描述
理 想 混 合 流 动 模 型
E(t) 1 et /
F (t) 1 et /
e d 1 0
2
2e d
1 1
0
流体流动
流体的流动特征：
指反应器内流体的流动状态和混合情况，它们随反应器的几何结 构（包括内部构件）和几何尺寸不同发生变化。由于反应流体在反 应器内流动的复杂性导致反应器内不仅存在流体流速的分布，更重 要的是还存在浓度和温度的分布。使得反应器内存在不同停留时间 的流体粒子以及不同停留时间流体粒子之间的混合即返混，从而导 致反应器内反应物料处于不同的温度和浓度下进行反应。影响反应 速率和反应选择性，使反应结果发生变化。
t≤0， F(t)=0 0＜t＜∞，0<F(t)<1 t＝∞， F(t)＝1。
E(t) dF(t) dt
1、数学期望
停
留 时 间
1.0
t 0 tdF(t) 0 tE(t)dt
分
布 的 2、方差
特
征 值
2 t
(t t)2 E(t)dt
0
t 2 E(t)dt t 2
0
停
脉冲法：
留
流体流动的描述
1、停留时间分布密度函数
停
非理想流动

非理想流动


（3）停留时间分布函数
在稳定连续流动系统中，同
时进入反应E器(t) 的N个流体粒子
F(t)
中，其停留时间小于t的面积那= 0 E部(t)dt 1.0 1.0
分粒子占总E粒(t1) 子数N的分率。
F(t1)
F(t1)
F (t) t dN
0N
t1
t
很显然: 当t=0时,F(t) 0;
E(t)
F(t) 0 E(t)dt 1.0
• 多级全混流串联模型的停留时间分布:
假设反应器总体积为VR，现由N个体积相等的全混釜串联组成。 对系统施加脉冲示踪剂A后，现对示踪剂A作物料衡算：
对第一釜 (i=1)应有：
0 v0CA1
dV1CA1 dt
①
CA0
0
CA1
C
dt V1 dCA1 t dCA1
v0 CA1
CA1
rA1
CA2
F (t) CA CA0
F (t)
dF (t)
1
t
dt
0 1 F (t) t 0
ln[1 F (t)] t t NhomakorabeaF(t) 1 exp[ t ]
E(t) dF (t) d [1 exp( t )] 1 exp( t )
t
dt dt
tt
t
E(t)
F (t)
1 t
1.0
0.632
t
t
t
（2）停留时间分布
理想反应器内所有反应物料的停留时间都是一样的。而 非理想流动使得反应物料的各个微元在反应器中的停留 时间长短不一，存在着一个停留时间的分布问题。
停留时间的长短直接影响反应的效果，停留时间越长， 反应进行得越完全。所以，对于非理想流动系统，我们 必须了解其停留时间的分布问题。本节主要讨论：阐明 流动系统的停留时间分布的定量描述及其实验测定方法。
10__第二章_反应器内流体流动与混合--非理想流动__297-2003(0)

10__第二章_反应器内流体流动与混合--非理想流动__297-2003(0)


间，调节釜数N就可以在全混釜与平推流反应
器之间确定某一种性能状态。
非理想连续流动的返混程度介于两种流动之间。
多釜串联模型把一个非理想流动的实际反
应器等价为N 个体积相同的全混釜串联反 应器，每个釜内达到完全混合，釜间没有
返混。
实际非理想流动反应器的停留时间分布等
价为釜数为 N 的串联全混釜的停留时间分
应器的管径较小、较长，物料在其中的流
速较快时，返混程度很小，此时可近似按
平推流进行分析与设计。
平推流反应器中所有物料质点的停留时间
都相同，且等于整个物料的平均停留时间。
采用脉冲示踪法测定平推流的停留时间分
布密度函数 E(t)
C(t)
C0 E(t)
t=0
t=0 t=0
t t tt
激励曲线
S
C 2 (t )
1
S
C1 (t )
1
S
(1 e

t
S
)
此一阶常微分方程可用积分因子法求解。
C 2 (t ) 1 e F2 (t ) C 2 (t ) C0
t
S
(1
t
S
t
) (1 t
C 2 (t ) 1 e
S
S
)
对第三釜作物料衡算，可得：
同样的停留时间分布可以是不同的返混造 成的。 不能直接用测定的停留时间分布来描述返 混的程度，必须借助于模型方法。
数学模型方法
分析器内复杂的实际流动状况，进行
合理的简化，通过数学方法来表述或关联 返混与停留时间分布的定量关系，然后再 进行求解。
建立流动模型的基本思想： 根据实测的停留时间分布，假设一种流动 状态，令这种流动状态下的停留时间分布 与实测结果一致，并根据假设的流动状态 的模型参数，结合在其中进行反应的特征
理想流动非理想流动理想流动反应器的分类和应用

理想流动非理想流动理想流动反应器的分类和应用


➢气液鼓泡反应器 因为气泡搅动所造成旳液体反向流动，形成很大旳液相循环
流量。所以，其液相流动十分接近于理想混合。 ①放置填料 ②设置多孔多层横向挡板，把床层提成若干级 ③设置垂直管
理想流动反应器旳分类和应用
分类 ➢ 理想混合流反应器 ➢ 理想平推流反应器 应用
实际生产中，连续操作釜式反应器能够近似看作是理 想混合流，连续操作管式反应器能够近似看作是理想平 推流。
降低返混程度旳措施
返混对反应器旳意义 ➢ 对反应过程产生不同程度旳影响 在返混对反应不利旳情况下，要使反应过程由间歇操作转 为连续操作时，应该考虑返混可能造成旳危害。选择反应器旳 型式时，应尽量防止选用可能造成返混旳反应器，尤其应该注 意有些反应器内旳返混程度会随其几何尺寸旳变化而明显增强。
➢ 在工程放大中产生旳问题
➢ 连续操作旳搅拌釜式反应器 为降低返混，工业上常采用多釜串联旳操作。当串联釜 数足够多时，连续多釜串联旳操作性能就很接近理想置 换反应器旳性能。(横向纵向？)
➢ 流化床 因为气泡运动造成气相和固相都存在严重旳返混。为了 限制返混，对高径比较大旳，常在其内部装置横向挡板 以降低返混；而对高径比较小旳流化床反应器，则可设 置垂直管作为内部构件（横向纵向？）
➢ 间歇反应器中不存在返混 ➢ 理想置换反应器不存在返混 ➢ 理想混合反应器返混到达极限状态 ➢ 非理想流动反应器存在不同程度旳返混
返混对反应过程旳影响
➢ 返混带来旳最大影响是反应器进口处反应物高浓度区旳消 失或减低。 ➢ 返混变化了反应器内旳浓度分布，使器内反应物旳浓度下 降，反应产物旳浓度上升。但是，这种浓度分布旳变化对反 应旳利弊取决于反应过程旳浓度效应。 ➢ 返混是连续反应器中旳一种主要工程原因，任何过程在连 续化时，必须充分考虑这个原因旳影响，不然不但不能强化 生产，反而有可能造成生产能力旳下降或反应选择率旳降低。
理想流动非理想流动理想流动反应器的分类和应用

理想流动非理想流动理想流动反应器的分类和应用

➢滞留区的存在 ➢存在沟流与短路 ➢循环流 ➢流体流速分布不均匀 ➢扩散
上述是造成非理想流动的几种常见原因，对一个流 动系统可能全部存在，也可能是其中的几种，甚至有 其它的原因。
返混及其对反应过程的影响
返混含义：专指不同时刻进入反应器的物料之间的混合， 是逆向的混合，或者说是不同年龄质点之间的混合。
理想流动 非理想流动 理想流动反应器的分类和应用
反应器内流体的流动特征主要指反应器内反应流体的流动状 态、混合状态等，它们随反应器的几何结构和几何尺寸而异。
反应流体在反应器内不仅存在浓度和温度的分布，而且还存在流 速分布。这样的分布容易造成反应器内反应物处于不同的温度和浓 度下进行反应，出现不同停留时间的微团之间的混合，即返混。
长径比较大和流速较高的连续操作管式反应器中的流体流 动可视为理想置换流动。
理想混合流动模型
含义：理想混合流动模型也称为全混流模型。反应物料以稳 定的流量进入反应器，刚进入反应器的新鲜物料与存留在其中 的物料瞬间达到完全混合。反应器内物料质点返混程度为无穷 大。
特点：所有空间位置物料的各种参数完全均匀一致，而且出 口处物料性质与反应器内完全相同。
种，其中重要的是__________。 连续搅拌釜式反应器为减少返混，工业上常采用________的操作
由于放大后的反应器中流动状况的改变，导致了返混程度 的变化，给反应器的放大计算带来很大的困难。因此，在分析 各种类型反应器的特征及选用反应器时都必须把反应器的返混 状况作为一项重要特征加以考虑。
降低返混程度的措施
降低返混程度的主要措施是分割，通常有横向分割和纵向分 割两种，其中重要的是横向分割。
理想置换流动模型
含义：理想置换流动模型也称作平推流模型或活塞流模型。 与流动方向相垂直的同一截面上各点流速、流向完全相同， 即物料是齐头并肩向前运动的。
化学反应工程 第四章 非理想流动1

化学反应工程 第四章 非理想流动1


(1)脉冲示踪法
在定常态下操作的连续流动系统的入口处，在t=0的瞬间输入M(g
或mol)的示踪剂A，并同时在出口处记录出口物料中示踪剂A的
浓度随时间的变化。
则：
M
0 v0CAdt
注：浓度CA是时间的函数
停留时间介于t~t+dt示踪剂的量：
M E(t)dt v0CAdt E(t) v0CA
M
t~t+dt内对A作物料衡算：
v 0 C A0 C A
d VC
dt
A
1 t
1
CA C A0
d
C C
A A0
dt
d
C C
A A0
dF
(t)
1 1
F (t)
dt
dt t
dF ( t ) 1 dt 1 F (t) t
确定积分上下限：0~F(0), t~F(t) 则：
F ( t ) dF ( t ) 1 t dt
对A作物料衡算： 切换后的t时刻，出口物料中示踪剂A在系统内的停留时间小于t， 而所占的分率应为F(t)，故 t 时刻 A 的物料衡算式：
v0CA v0CA0 F(t) or : F(t) CA
C A0
因此，由出口物料的CA~t曲线可获得F(t)曲线。 图示为：
阴影部分的面积= 0 C A 0tdA C0 1 .0tC A 0d(F t)C A 0t
t
2 1
r
2
t R
r
2
1
t
代入上式
R
2t
2
F
(t)
1
t 2t
2
dF ( t ) t
E (t)
dt
反应过程与设备例题与习题(第三章)

反应过程与设备例题与习题(第三章)

第三章非理想流动一、主要基本理论、基本概念1.停留时间：物料质点从进入反应器开始，到离开为止，在反应器中总共停留的时间。

2.平均停留时间：整个物料在反应器内平均停留的时间。

3.停留时间分布密度函数E(t)同时进入反应器的N 个流体质点中，停留时间介于t 与t+dt 之间的质点所占的分率dN/N 为E(t)dt 。

1)(0=⎰∞dt t E4.停留时间分布函数F(t)流过反应器的物料中停留时间小于t 的质点(或停留时间介于0～t 之间的质点)分率。

⎰=tdt t E t F 0)()(5.停留时间分布的数字特征 ① 数 学期 望 t =⎰⎰∞∞0)()(dtt E dt t tE② 方 差2t σ=⎰⎰∞∞-02)()()(dtt E dtt E t t③ 无因次方差22//t tt t θσσθ==6.停留时间分布的实验方法及对应曲线 ① 脉冲示踪 E(t) 曲线 ② 阶跃示踪 F(t) 曲线 ③ 无因次化 /()()()()t tE tE tF F t θθθ===7.理想流动模型的停留时间分布① 平推流 001()()1t t E t E t t θθθ≠≠⎧⎧==⎨⎨∞=∞=⎩⎩ 001()()111t t F t F t tθθθ〈〈⎧⎧==⎨⎨≥≥⎩⎩2210t t θτθσσ====② 全混流 ()1/exp(/)()E t t t t E e θθ-=-=()1exp(/)()1F t t t F e θθ-=--=-2/1t t tθτθσ===8.非理想流动模型的停留时间分布①扩散模型：是在平推流模型的基础上再迭加一个轴向扩散的校正，模型参数是轴向扩散系数Ｄl （或P e 数），停留时间分布可表示为Ｄl 的函数。

适用于返混不大的系统。

Pe >100时: θ=1 22/2/t t Pe θσσ==闭 式: θ=1222/2/(1)Pe Pe Pe e θσ-=--②多级串联全混流模型：是用m 个等体积的全混流模型串联来模拟实际反应器。

化学反应工程-第4章

化学反应工程-第4章




0
E ( )d 1
21
无因次化方差
( 1) E ( )d
2 2 0
0
t t 2 ( 1) tE (t )d t t
2 1 2 2 (t t ) E (t )dt t2 t 0 t
2
t2
t
2
可推知：平推流 0
dV1C1 dt
(C0 M ) Q0
(1)
(2)
将式(1)积分后可得：
C1 1 t exp( ) C0 t1 t1
(3)
38
对第二全混流区(i=2)应有：
dV2C2 Q0C1 Q0C2 dt 将(3)代入(4)得：
Q0 dC2 Q0 1 t C0 exp( ) C2 V2 t1 t1 dt V2
0 F (t ) 1 0 F ( ) 1 tt tt
tt tt
1 1
1 1
统计特征值： 1
2 0
28
2. 全混流模型
考察有效体积为Vr、进料体积流量为Q的全混流 反应器，若在某一瞬间t=0，将流体切换成流量相 同的含有示踪剂的流体，同时检测流出物料中示踪 剂浓度变化。

E( ) exp[ ]
E ( )d e d 1
0 0
E ( )d 1 e d 1 1
2 2 0 0

2

2
小结
1.全 混 流
t2 t 2 2 1
2.平 推 流
3.工业反应器
E(t) F(t)
1
1.0
0
t
t
0

《非理想流动》课件


能量方程
总结词
描述流体能量守恒的方程
详细描述
能量方程是流体动力学的重要方程之一，它表达了流体能量 守恒的原理。该方程包括流体的内能、动能和势能的变化率 ，以及作用在流体上的各种热力和机械力的能量传递。
状态方程
总结词
描述流体状态变化的方程
详细描述
状态方程是描述流体状态变化的数学表达式，它通常表示流体的压力、体积和温度等状 态变量之间的关系。对于不同的流体，状态方程的形式和参数也不同，例如理想气体状
环境工程领域
总结词
非理想流动理论在环境工程领域中具有重要 应用，有助于解决环境问题并提高环境保护 措施的效果。
详细描述
在环境工程领域，流体流动是许多环境问题 和治理措施的核心。非理想流动模型能够更 准确地描述污染物在水域、土壤等环境中的 迁移和扩散过程，帮助环境工程师制定更有 效的治理方案。例如，在设计污水处理厂时 ，考虑非理想流动的影响，可以更准确地预
非均匀性是指流体的流动参数 在空间上分布不均匀，导致流 场中不同位置的流动状态存在 差异。
产生原因
非理想流动的产生原因多种多样，主要包括流体本身的物理性质、流动参数和边 界条件等因素的变化。
例如，流体的粘性、压缩性和热传导性等物理性质对流动状态产生影响；流体的 速度、压力和温度等流动参数的变化也会导致流动状态发生变化；此外，流体的 边界条件如管道形状、进出口位置等也会对流动状态产生影响。
应用场景
常用于分析具有相似流动特征的不同 实验数据。
优点
能够消除物理量纲的影响，使不同实 验数据具有可比性。
缺点
对流动特性要求较高，某些情况下可 能无法得到准确结果。
05
非理想流动的应用领域
流体机械设计

化学反应工程 第四章

V V 'RA V 'RB
在t时对出口处的示踪物B作物料衡算：
所以，
VC V 'RA 0 V 'RB C0
C V 'RB C0 V
＝停留时间≤t的示踪物溶液体积所占分率最后得：F(t)(
C C0
)
s
3.脉冲法
1）实验步骤
（1）物料保持稳定流动
（2）在一瞬间注入示踪剂B，总量是M，在体积流量V中的
t tm＝t
则
2 t
t2E(t)dt
2
t
0
0
对离散型测定值，
t2E(t)
2 t
0
tm2
E(t)
0
三、对比时间 为了方便起见，常用对比时间作为变量。 对比时间的定义
t
tm
1.平均对比停留时间
tm 1
tm
2. E( )
3. F ( )
E( )
dF ( ) d
dF ( )
d( t )
浓度为Co 。数学描述为 0 t 0
C C0 0 t t0
0 t t0
c(∞)
C0
C(t)
t0
V ( M )Ccp(t)
0
0
t=0
t
（３）以t＝0为计时基准，检测出口处的B浓度C。
响应t 曲线 t
（４）标绘
V
( M
)C p
~
t
曲线
２）( V
M
)Cp
?
在出口处作示踪物B的物料衡算：
V C dt Mt
在实际 反应器中，物料可能是由固体颗粒、液滴、气泡或者 分子团块等聚集体组成的，称之为微团。微团之间的混合程度 有三种情况，

9__第二章_反应器内流体流动与混合--非理想流动__1_97-2003

F(t) 1.0
t N E (t )dt 1 0 N
拐点
0
t
2.停留时间分布积累函数 F(t)性质 (1) t = 0时，F(t) = 0； t = ∞时，F(t) = 1； (2) 0 ≤ F(t) ≤ 1； (3) F(t)是一个单调不减函数； (4) dF(t) / dt = E(t) ，F(t)为一无因次数； (5) 左连续； 有的书因采用定义不同，则为右连续。
C (t )dt N Q N 示踪
作图，则每一个矩形的面积为△N/N，表示停
留时间为t→t+△t的物料占总进料的分率。
如果假定红色粒子和主流体之间除了颜色
的差别以外，其余所有性质都完全相同，
那么就可以认为这 100 个粒子的停留时
间分布就是主流体的停留时间分布。
假如示踪剂改用红色流体，连续检测出口中红色
流体的浓度，如果将观测的时间间隔缩到非常小
0
t
停留时间小于t的粒子分率：F (t ) E (t )dt
0
t
0
a a
b
t t
0
b
b
停留时间介于（a, b）之间的粒子分率
F (t ) F (a) F (b) E (t )dt
a
当 t → ∞时，t = 0同时进入反应器的 N 个质点全部流出反应器，故有：
F (t )t
3.停留时间分布密度函数曲线 以 E(t) 纵轴，t 为横轴，作图，得到 E(t) 对 t 的停留时间分布密度函数曲线，如下图。 E(t) E(t)dt
t
dt
4.停留时间分布密度函数曲线的几何意义
图中曲线下微小的矩形面积 E(t) dt 表示停

no13-非理想流动反应器-槽列模型


1
1 1 k i
(18) (19)

X N 1 串联槽总的的转化率为：
C A, N
1
1 N 1 (1 X ) A , i (1 k i ) N
对于任意第i槽无聊流中的A物质进行物质衡算得到：
q (CA, i 1 CA, i ) rA, iVi 0,同时除以q 得(CA, i 1 CA, i )
N 1时,E1 1 1 e , N 2时，输入Ein ,2 E1 e 。 ti ti
（11）
第二槽的输出等于第三槽的输入，不用进行质量衡算 而由卷积分直接求出，写成积分形式，则两槽串联时 总的输出为： Eout (t ) 0t Ein (t ) E (t t ) dt , 其中E (t t )为第二槽的分布 根据式（11）和（12）可以得到类似的： 1 t / ti 1 (t t )/ ti Ein(t ) e 和E (t t ) e ti ti 将式（13）代入式（12）得到： t t / ti tiEout (t ) e ti
则槽列模型串联槽数N的值等于扩散模型参数Pe(uL/De) 的一半。
v0 v0
确定每槽的未转化率即求式（21）的根，用牛顿迭代法 可以求解。则总的转化率为： CA, N (22) X A 1 12 n1n 1
CA,0
C A,i 1 CA,i 2k n 1 令i i CA,i 1 , i , 则式（20）变为f ( ) n 1 0. 2 CA,i 1 2
（1）
槽列模型
整理后得：
n n e
1 o
qvt / vi
（2）
vi n0 n1 t 1, 令 1=t / t 1, 根据F出口曲线F1= , qv n0

简述非理想流动轴向扩散模型的特点

简述非理想流动轴向扩散模型的特点
非理想流动轴向扩散模型是一种描述气体在管道内传输过程中扩散现
象的数学模型，它主要描述了气体分子在通道内的扩散、漂移、反弹和碰
撞等过程，并考虑了通道内多种因素对扩散现象的影响。

其主要特点包括：
1.非均匀性：在通道内，气体分子的扩散速度和漂移速度不是均匀的，由于通道内多种因素的影响，如气体浓度、压力、温度等因素，使得通道
内各点的速度和浓度都不相同。

2.非对称性：在通道内，气体分子的扩散和漂移方向不是完全对称的，即通道内上下、左右、前后等方向的扩散和漂移速度不同。

3.慢速性：由于分子的质量很小，分子速度很快但是能量很小，因此
扩散速度比较慢，需要较长时间才能完成。

4.离散性：气体分子是单个分子的运动，每个分子相互之间的运动是
随机的，因此扩散现象具有一定的离散性，即每个分子的轨迹和速度都是
不同的。

5.连续性：尽管气体分子的运动是随机的，但是通道内整体的气体浓
度和压力是连续的，即通道内任意两点之间的浓度和压力都可以连续地变化。

简述非理想流动轴向扩散模型的特点

简述非理想流动轴向扩散模型的特点非理想流动轴向扩散模型是一种流体力学中常用的模型，用于描述流体在管道中的流动过程。

与理想流动模型相比，非理想流动轴向扩散模型更加接近实际流动情况，能够考虑一些现实流动中的特点。

首先，非理想流动轴向扩散模型考虑了粘滞效应。

在理想流动模型中，常常假设流体是无粘性的，即粘滞力可以忽略不计。

而在实际流动中，由于流体黏性的存在，粘滞力会对流动的控制和分布起到重要的作用。

非理想流动轴向扩散模型引入了粘滞力的计算，考虑了粘滞效应对流速分布的影响。

其次，非理想流动轴向扩散模型考虑了管道内壁的摩擦阻力。

在理想流动模型中，常常假设管道内壁是光滑的，无阻力。

而实际情况中，管道壁面的摩擦阻力会对流动产生影响，并且随着流速的增加，摩擦阻力的作用也会增大。

非理想流动轴向扩散模型引入了壁面摩擦阻力的计算，使得流速的分布更加真实。

另外，非理想流动轴向扩散模型考虑了管道内壁的粗糙度。

在实际流动中，管道内壁常常存在一定的粗糙度，粗糙壁面会增加流体流动的摩擦阻力，降低流体的流速。

非理想流动轴向扩散模型通过引入管壁的相对粗糙度，考虑了壁面粗糙度对流动的影响。

此外，非理想流动轴向扩散模型还考虑了流体的压缩性。

在理想流动模型中，常常假设流体是不可压缩的，即流体密度在流动过程中保持不变。

而实际情况中，流体在高速流动时会产生压缩效应，流体密度发生变化。

非理想流动轴向扩散模型引入了压缩性的计算，使得流动过程更加真实。

最后，非理想流动轴向扩散模型还考虑了流动中的传热过程。

在一些特定情况下，流体的温度分布对流速的分布起到重要的作用，如流体传热过程中的对流传热、流体的温度梯度对流动产生的影响等。

非理想流动轴向扩散模型引入了传热过程的计算，使得流动过程更加复杂和准确。

综上所述，非理想流动轴向扩散模型相比于理想流动模型更加真实和复杂，考虑了粘滞效应、管道壁面的摩擦阻力和粗糙度、流体的压缩性以及流动中的传热过程等因素的影响。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

xA
1 exp
0
kt c
c
1
0.3347
0.6653
多级串联槽模型
• 物理模型： • 反应器是由若干大小相等的全混流反应器
串联而成。 • 这些全混流反应器之间没有返混，没有反
应。 • 定常态操作。
平推流与全混流的比较
1 (-rA )
平推流
= VR
V0
=cA0
dx xAf
A
0 (-rA )
Nc3
Nc2
Nc0
1
e N
1
N
解得：
c3
c0 1
e N
1
11！N
1 N
2!
2
依此类推：
cN
c0 1 eN
1 11！N
1 N
2!
2
......
N
1
1!
N
N1
cN
c0 1 eN
1 11！N
1 N
2!
2
......
N
1
1!
N
N1
由定义：
cN F
c0
因此：
F
1
e N
1
11！N
1 2!
N
2
......
N
1
1!
N
N
1
由E dF
d
E
Ne N
1
11！N
1 N
2!
2
......
N
1
1!
N
N 1
Ne N
1
11！N
1 2!
N
2
......
N
1
2!
N
N 2
E
N
N 1!
N
e N 1 N
N N e N 1 N
N 1!
E d
0
0
NNN1!
N
e
N
d
流出
ATu
cA
cA l
dl
反应
rA ATdl
积累
cA t
ATdl
轴E向扩clA 散AT出
• 整理得：
E
2cA l 2
u
cA l
cA t
rA
0
对示踪实验，rA 0，因此
cA t
＝E
2cA l 2
u
cA l
无因次化： 令c cA , t , z l
cA0
L
c
E uL
2c z 2
• N等于某一值，意味着该反应器的返混程 度相当于N个理想混合反应器的串联。
• N只是一个虚拟值，因此，N可以是整数
也可以是小数。
2 θ
1 N
• 停留时间分布密度函数的散度为槽数的 倒数。
• 小数的阶乘由Γ函数解决。
z u z1eudu 0
n 1 n!
x x 1,
x
x x 1x 1
NVRi
V0
t
则：
由Vci1
Vci
VRi
dci dt
得：
dci
d
Nci
Nci1
BC : 0t 0, ci 0
对第一槽 解得：
dc1
d
Nc1
Nc0
c1 c0 1 eN
对第二槽
dc2
d
Nc2
Nc1
Nc0
1
e N
解得： c2 c0 1 eN 1 N
对第三槽
dc3
d
凝集流模型
• 物理模型： • 流体以流体团的方式流过反应器，这些流
体团彼此之间不发生混合，每个流体团相 当于一个小反应器。由于返混的作用，流 体团在反应器内的停留时间不同，达到的 转化率因而不同，在反应器出口处的宏观 转化率，就是各不同停留时间的流体团达 到的转化率的平均值。
• 这样就把流体的停留时间分布与反应转 化率联系起来了，每个流体团都作为一 个间歇反应器，它的反应时间由停留时 间分布决定。而流体团在停留时间内达 到的转化率由反应动力学决定。最后， 将二者结合起来，在出口处加权平均， 得到最终转化率。
xneaxdx
0
n!
a
n1
所以：
NN
N 1!
N! N N 1
1
2
0
2 E d
2 E
d
2
0
2
NN
2
N 1eN d
0 N 1!
NN
N 1eN d 1
0 N 1!
NN
N 1!
N
N
1!
N 2
1
N N 1 1
N2
1 N
• N=1，全混流
• N ，平推流
• 相当于若干平推流反应器或间歇反应器 的并联，将非理想流动对反应的影响明 显化了。
• 写成数学公式：
停留时间在t和t t之 停留时间在t和t t
xAf t0 间的微元达到的转化率 之间的微元的分率 如果是连续函数：
xAf
0
xA
E
t
dt
或
xAf
1 0
xAdF
t
xA－－单个微元的转化率，当然是t的函数。
• 例3-3某非理想流动反应器，其停留时间分 布规律同例3-2。在该反应器内进行一级反 应，动力学方程为-rA=3.33×10-3cA，请确 定该反应器的出口转化率（反应物A的化学 计量系数为1）。
• 解：采用凝集流模型进行计算。
• 对于一级反应，在间歇反应器中转化率 与反应时间关系如下：
t
• 费克扩散定律(Fick’s law)：
NA
E
dcA dl
NA : kmol m-2s-1
E : m2s1
• 在有化学反应时对反应物做物料衡算：
ATucA
AT
u
cA
cA l
dl
E
cA l
AT
dl
E
l
cA
cA l
dl
AT
流入 ATucA
E
轴向扩散入
l
cA
cA l
dl
AT
c z
L :反应器总长
令： Pe uL 彼克列Peclet 数
E c 1 2c c
Pe z2 z
Pe的物理意义：流动量与扩散量的比值, 数值越大返混程度越小。 扩散系数E ，则Pe 0,全混流 扩散系数E 0，则Pe ,平推流 不同的边界条件会有不同的结果。 依流体进出反应器时是否发生流型变化， 共有四种边界条件
cA0
xA 0
dxA rA
cA0
xA 0
dxA kcA0 1 xA
1 ln k
1
xA
xA 1 exp kt
xA
0
xAiF t
1
0
exp
k tF t
1
exp
0
kt
c
c
时间 t/s
0 120 240 360 480 600 720 840 960 1080 Σ
示踪剂浓度 c/g.m-3
全混流
VR V0
cA0
xAf xA1 rA f
xA
• 用阶跃法测定第i个反应器的停留时间分布
V0, c0,
V1,c1,
V2,c2,
Vi,ci,
Vn,cn
t时刻，对第i个反应器的示踪剂做物料衡算：
输入量 Vci1
输出量 Vci
积累量
VRi
dci dt
恒容且每个CSTR的容积为VRi ,总容积为NVRi ,
0 6.5 12.5 12.5 10.0 5.0 2.5 1.0 0 0 50
ΔF(t)
0 0.13 0.25 0.25 0.20 0.10 0.05 0.02
0 0
exp
kt
c
c
0 0.0872 0.1124 0.0754 0.0464 0.0136 0.0045 0.0012
0 0 0.3347
称函数递推公式。
手册可查1 x 2的函数值，
其余通过递推公式求得。
• 解题步骤：
停留时
t
2 t
2 θ
N
对等温一级不可逆反应，前一章有：
xAN
1
1
1
k i
N
式中： i N
轴向扩散模型
• 物理模型：
• 1 主体流动为平推流，但叠加一涡流扩 散。
• 2 涡流扩散遵循费克扩散定律且在整个 反应器内扩散系数为常数。