图形规律思维导图

思维导图（Mind Mapping），又叫心智图，是表达发射性思维的有效的图形思维工具，是一种将放射性思考具体化的方法。

思维导图运用图文并重的技巧，把各级主题的关系用相互隶属与相关的层级图表现出来，把主题关键词与图像、颜色等建立记忆链接，思维导图充分运用左右脑的机能，利用记忆、阅读、思维的规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能，思维导图因此具有人类思维的强大功能。

思维导图是英国学者博赞（Tony Buzan）在20世纪60年代初期所创，将其应用于教学可实现以下价值：1．帮助师生掌握正确有效的学习方法策略，更快更有效的进行课本知识的传授，促进教学的效率和质量的提高。

在制作思维导图的过程中，会涉及到如何快速的阅读和信息整理的内容，通过在整理和绘制思维导图的过程关键词和核心内容的查找可以更好的帮助老师和学生们，加强对所学知识的理解并将所学内容进一步的加以深化。

2．建立系统完整的知识框架体系，对学习的课程进行有效的资源整合，使整个教学过程和流程设计更加的系统、科学有效。

利用思维导图进行课程的教学设计，会促成师生形成整体的观念和在头脑中创造全景图，进一步加强对所学和所教内容的整体把握，而且可以根据教学过程和需要的实际请客做出具体的合理的调整。

3．教学过程采取互动式，促进师生间的交流与沟通，打破了传统的一言堂。

在应用思维导图教学的过程中，学生为主体，教师作引导，可以充分发挥学生学习的主观能动性和创造天赋。

在进行思维导图教学的过程中，教师的作用主要是作积极正面的引导，并指导和回答学生在完成学习任务的过程中所遇到的问题。

师生间可以比较自由的交流和沟通，所以可以让学生有更大的发挥自我的空间，让学生根据自己的实际情况制定各自的学习计划从而做出合理的安排。

4．在教学过程中，可以做到关注整体，关怀个体，从而实现真正意义上的因才施教，发展并挖掘个体的独特性。

通过学生的思维导图作品，能够发现每个学生的知识结构，发现其对所教课程的理解和认识程度，从而可以对于学生所存在的具有共性的问题做出具体的指导和相应的教学方案。

小朋友，你已经学习了“方和圆”的相关知识，你发现了吗？生活中因为有了棱角分明的“方”而个性鲜明，有了完整和谐的“圆”而婀娜多姿，当方形和圆形巧妙组合后，方圆之间就有了更多的数学奥秘。

思维导图绘“方圆”□武国芬吕维智r r2rS 大方=（2r ）2=4r2S 圆=πr 2=3.14×r 2S 圆=πr 2=3.14×r 2S 小方=12×2r ×r ×2=2r 2S 大方-S 圆=4r 2－3.14×r 2＝0.86r 2S 圆-S 小方=3.14×r 2-2r 2＝1.14r 2我们把正方形与它里面最大的圆组合成的图形称为“方中圆”，把圆与它里面一个最大的正方形组合成的图形称为“圆中方”。

如果两个圆的半径都是r ，那么方、圆的面积有怎样的关系呢？你能从中发现哪些值得研究的数学问题呢？下面我们先对方圆之间的面积关系来做一下分析（如下图）。

无论圆的大小如何改变，方内画一个最大的圆（方中圆），正方形与圆相差的面积都是半径平方的0.86倍；而在圆内画一个最大的正方形（圆中方），相差的面积都是半径平方的1.14倍。

小朋友，除此之外，你还能发现哪些有意思的规律呢？我们继续研究。

因为两个圆的面积相等，所以我们可以把两个圆重合，这样“方中圆”与“圆中方”这两个图形就合并成了一个图形（如下图）。

此时大正方形与小正方形的面积有什么关系呢？大正方形的面积是小正方形面积的2倍，两个正方形的面积比是：4r2∶2r2=2∶1，两个正方形之间的面积是4r2-2r2=2r2。

我们进一步延伸思考：方、圆的面积比是否也具有一般规律呢？尝试分析如下：“方中圆”大正方形的面积与圆的面积比是：S大方∶S圆=4r2∶πr2=4∶π；“圆中方”圆的面积与小正方形的面积比是：S圆∶S小方=πr2∶2r2=π∶2。

小朋友，我们把以上方、圆之间面积的关系用思维导图进行整理，归纳总结方圆面积关系的一般规律如下页图所示。

平面图形：
有些几何图形（如线段、角、三角形、长方形、圆等）的各个部分都在同一平面内，它们是平面图形。

如直线、射线、角、三角形、平行四边形、长方形（正方形）、梯形和圆都是几何图形，这些图形所表示的各个部分都在同一平面内,称为平面图形。

例如：有一组对边平行的四边形一定是平面图形。

（两条平行线确定一个平面）
平面图形的大小,叫做它们的面积
点的形成是线，线的形成是面，面的形成是体。

平面图形：有些几何图形（如线段、角、三角形、长方形、圆等）的各个部分都在同一平面内，它们是平面图形。

常见的平面图形图示:
从左到右依次为:长方形、正方形、三角形、圆、椭圆、
菱形、五边形、六边形。

平面图形分类:
几何图形知识体系图:
平面图形有哪些
基本的平面图形：直线、射线、长方形、正方形、三角形、平行四边形、梯形、圆形等等。

平面图形是几何图形的一种。

平面几何图形可分为以下几类：1.圆形：包括正圆、椭圆等；2.多边形：三角形、四边形等；3.弓形：优弧弓、抛物线弓等；4.多弧形：月牙形、太极形、葫芦形等。

什么是平面图形
平面图形是几何图形的一种，指所有点都在同一平面内的图形，如直线、三角形、平形四边形等都是基本的平面图形。

平面图形是平面几何研究的对象。

几何图形，即从实物中抽象出的各种图形，可帮助人们有效的刻画错综复杂的世界。

生活中到处都有几何图形，我们所看见的一切都是由点、线、面等基本几何图形组成的。

几何源于西文西方的测地术，解决点线面体之间的关系。

无穷尽的丰富变化使几何图案本身拥有无穷魅力。

行测图形推理动态位置变化移动图形在平面上的移动，图形本身的大小和形状不发生改变，分析移动规律时要找准移动的方向和距离考法旋转时针法区分旋转和翻转的区别箭头法判断图形方向和角度翻转时针法区分旋转、翻转左右翻转与原图形竖轴对称；上下转与原图形横轴对称静态位置关系元素一般不同，每幅图形的元素相对位置呈某种规律线复杂图形的位置叠加和遍历（元素相似）叠加的考法完全叠加叠加与动态位置变化的结合遍历：所有都经历一遍考法：与位置结合考察属性和数数（元素凌乱）数点：交点、切点只数十字交叉点普通交点和十字交叉点一起数只数直线和曲线的交点（图形由为数不多的直线曲线构成）只数切点交点和切点一起数特殊点：线段出头数；黑白点（黑白分开数）曲直线和数线曲直线：全直、全曲、半曲半直数线的考法直角图形与数角直角图形数角（锐角、直角总数；内角、外角）封闭性和数面封闭和开放封闭性的考法数面的考法数部分和元素部分和元素的区别数元素的考法对称性和数对称轴对称性数对称轴的考法一笔画路径不重复不中断的线条就是一笔画汉字的考法静态位置关系（左右结构、上下结构叠加遍历封闭性和数面数笔画技巧字母和数字的考法数点曲直线和数线封闭性和数面数部分和元素对称数笔画六面体基础知识考法：折纸盒和拆纸盒向内折，折完保证能看到图案展开图呈“Z"字型的能折成六面体呈90度夹角的面可旋转90度，使相邻两边重合展开图的向对面在立体图中只能出现一个解题方法时针法公共边法橡皮法特殊考点立体图形三视图：主视图、俯视图、侧视图截面图实物重组（缺啥补啥）平面图形重心凹凸性意指图形（实指图形）其他考点图形相似两步走元素构成一致的图形有相同元素但元素有增减时相异图形找共性对称性直曲性封闭开放性。

数学几何图形概念思维导图几何是研究空间和形状的数学分支。

在几何中，图形是最基本的概念之一。

图形是由一组点和它们之间的连接线组成的。

在数学中，几何图形可以通过概念思维导图来清晰地展示和总结。

概念思维导图是一种以图形化方式展示信息和构建关联的工具。

它通过将主题和子主题以及它们之间的关系用图形表示出来，帮助我们更好地理解和记忆知识内容。

下面是一个数学几何图形概念思维导图的示例：(图片描述：概念思维导图)圆形是一个基本概念，它由一个具有相同半径的圆心和一条半径组成。

圆形在几何中非常常见，它具有许多重要的性质。

其中一些性质包括：1. 直径：直径是通过圆心的任意两点的线段，它的长度等于圆的半径的两倍。

2. 弧：弧是圆的一部分，它由一个起点、一个终点和一个连接这两点的曲线组成。

3. 弧长：弧长是圆上的弧的实际长度。

它可以通过圆的周长和圆心角的度数来计算。

4. 正切：正切是从圆心到圆上某个点的直线与半径的比值。

在三角函教程中，正切是一个重要的概念。

接下来，我们来看看另一个常见的几何图形——矩形。

矩形是一个有四个直角的平面图形。

它有一些重要的性质，如：1. 面积：矩形的面积等于其长度乘以宽度。

2. 对角线：矩形的对角线是连接相对顶点的线段，它们相等且交于中点。

3. 周长：矩形的周长是所有边长的和。

除了圆形和矩形之外，还有许多其他几何图形的重要概念需要我们掌握。

例如三角形、正方形、梯形等等。

每个图形都有其独特的性质和公式，通过概念思维导图，我们可以有效地组织和记忆这些知识。

几何图形的理解对于解决实际问题和应用数学知识至关重要。

无论是在建筑设计、地理测量还是计算机图形学等领域，几何都扮演着重要角色。

因此，我们应该努力学习和掌握几何图形的概念和性质。

通过本文的思维导图，我们可以清晰地了解和回顾数学几何图形的相关概念。

希望这个思维导图能帮助你更好地理解和应用几何知识，提高数学学习的效果。

让我们一起努力，探索数学的美妙世界！。

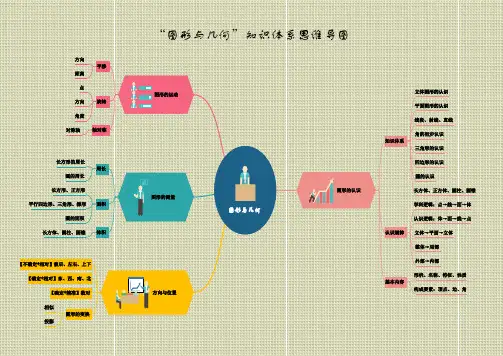
“图形与几何”知识体系思维导图
图形与几何
图形的认识
图形的测量
方向与位置
图形的运动
知识体系
认识规律
基本内容
立体图形的认识
平面图形的认识 线段、射线、直线 周长
面积
体积
长方形、正方形
平行四边形、三角形、梯形
【不确定+相对】前后、左右、上下
【确定+相对】东、西、南、北
【确定+精准】数对 图形的变换
平移
旋转
轴对称
点
方向 角度 相似
投影
角的初步认识
三角形的认识
四边形的认识
圆的认识
长方体、正方体、圆柱、圆锥 学科逻辑：点→线→面→体 认识逻辑：体→面→线→点 立体→平面→立体 整体→局部 外部→内部
形状、名称、特征、性质
构成要素：顶点、边、角 方向
距离 对称轴
长方形的周长
圆的周长 圆的面积
长方体、圆柱、圆锥。