图形推理史上最全思维导图

一、位置规律 1.平移
2.旋转、翻转
二、样式规律 1.遍历
2.加减同异
3. 黑白运算
三、属性规律 1.对称性 轴对称图形（“等腰”元素）： 中心对称图形（字母“S”、“Z”、“N”、平行四边形）： 轴对称+中心对称图形： 2.曲直性 全直
全曲 有曲有直 3.开闭性 全开放：
全封闭： 半开半闭：
四、数量规律 1.点 （1）曲直交点
（2）框上、内交点 2.线 （1）直线
（2）曲线
（3）笔画数 “日”字及其变形图 “田”字及其变形图
“圆”相切或相交 多端点图 （4）平行线
3.角 4.面 （1）整体数面 （2）所有面的形状 （3）相.图形间关系 相离：
相交于点：
相交于线：
相交于面：
2. 功能元素 标记点： 标记线： 标记面： 标记角： 特殊功能元素：

翻转的方向——左右翻转：竖轴对称，左右对调、上下不变。上下翻转： 横轴对称，上下对调、左右不变。 翻转 翻转的角度——180度旋转：上下左右对调 整体翻转——也整体（6个图）翻转/旋转形成新的图形
１
1.简单叠加，叠加后求同/求异（抓住1-2条线突破）；
叠加
2.位置变化（旋转/翻转）+求同/求异；行和列分别用不同的叠加规律。 ⚠要注意辨析：谁叠在谁的上面、谁被覆盖；区分部分叠加VS完全叠加、
优先考虑——切不出来的图形，用排除法。 六面体：六面体只能切出锐角三角形，切不出直角三角形、钝角三角形。 截面 圆柱：圆柱斜切得到弧线，不可能切出梯形。 图 ⚠️注意：空心没有实线；不同角度的截面无法共存，即刀不能拐弯切（eg. 不能外部横切矩形、同时内部斜切椭圆）；刀切过圆柱的弧面得到的是曲 线；关注切面的角（直角/锐角）；辨析实心和空心的颜色。
２
数量 规律
交点特征——有出头色彩，如十字形、T字型、L字型 曲直交点特征——图形均为类圆曲线，圆和弧线多且曲直相交 切点特征——类圆曲线+点连接 圆内交点——每幅图都仅有一个圆，线条贯穿圆内外 点 其他考点——曲曲/直直交点数（和/差），内外交点（图形均有外框，内 外分开看：内部交点、外部交点、内外交点的和/差），黑点/白点连接形 成的部分数，线条经过或覆盖的点的数量，点在四个角的位置移动，相连 黑圆圈的数量变化（eg.各行分别有1、2、3个黑圆相连）
３
属性 规律
对称的考点主要有：对称方式，对称轴数量/方向，对称轴两侧空间的形 状，对称轴经过的点/线/面的数量。 1.轴对称——提示点：等腰三角形/梯形、箭头及其变形、五角星、一边一 个相同元素（如Y）。 具体考点——对称轴的方向/数量，对称轴与图形中某点/某线的关系（对 称轴经过交点/直线/与线重合），对称轴的自身的角度，对称轴旋转的角 度，字母和汉字要注意书写笔画长短/大小是否严格符合对称性，对称轴是 对称 否经过所有面，最大/最小面的对称性，两个对称图形要考虑对称轴之间的 关系。 2.中心对称——旋转180度后完全重合；两个相同图形反着放。提示点：平 行四边形，S、N、Z字型，风车及其变形。 3.轴+中心对称——存在两条互相垂直的对称轴。 4.整体对称：图形米字型整体对称，五个图以第三个图为轴成轴对称，白块 /黑块的整体对称性，对称轴的数量对称（如对称轴数量分别为 4/1/2/2/1/4）。

一般递增或递减是按照1，2，3，4的顺序
步数恒定的 步数有序加减的
步数
平移（黑白块问题）
一般都是循环的，但也要注意来回弹着跑的
路径
顺时针 逆时针
方向
45度，60度，90度，120度，135度，180度
旋转角度
旋转
元素组成相同（位置规律）
上下翻转，左右不变 左右翻转，上下不变
翻转
不动的部分优先看
注意比较选项差异
三图对于列的黑块数相同
行列同时移动看
三图对应行和列的黑块数均不同
思路
上下左右
不动的黑块优先看
技巧
方向
有时黑块减少是因为移动后重叠
特征：黑块只在最外圈出现
确定时针移动的方向，区分不同的黑块
思路
顺逆时针
如果只有两个黑块，那就看中间隔的白块数量
技巧
每次走固定步数，一般是按照2，2，2的步数
如果是九宫格，注意观察两个黑块的相对位置，相对位置 保持不变
原来被遮挡的看不到
先观察图形，能第一眼看出结论即选
第一眼看不出结论，去观察选项 勾出特殊或不同的图去进行比较
关于分组
图形推理
两个相对面同时出现，排除 两个相对面同时都没出现，排除
相对面
空间重构
公共边不变
相邻面
圆柱：上下切 六面体：上下、斜、拦腰切
圆锥：沿着顶点向下切 六面体：沿着棱上某一点斜切
截面有矩形
截面有三角形
截面图
空间类
立体图形本身有弧线则拦腰或斜切均可以 主视、俯视、左视
截面有弧线 三个角度
剖面图
原来有线才有线
三视图
推理总结
先观察整体，后观察部分

【干货】学会这8张思维导图,再复杂的知识都能轻松拿下父母在家就能指导孩子，推荐收藏。

投稿邮箱：***************你读书时候是不是有一类学生？他们学习不熬夜，考前不突击，但是门门课成绩都很好，爸妈说这叫“天资过人”。

去年同学会，我重逢那位“天资过人”的老同学，聊起对他的羡慕时他谦虚说：“大家的智商都差不多，可能我学习方法比较好。

”然后他就把当年的笔记给我看，大概是这样的——手绘思维导图示意图（图片来源于网络）后来我知道，这就是“思维导图”（Thinking Map），一种图形思维工具。

在美国新加坡思维导图已经成为小学生的必修课，近几年国内热度也上来了。

思维导图的理论是“可视化思维”（Visible Thinking）。

1967年，哈佛大学教育学院成立“零点计划”，对思维方式进行研究，其中一个明星项目就是“可视化思维”——被可视化的思维更有利于理解和记忆，现在已经是一种比较公认的高效学习方法了。

回过头再想，当年我们学习遇到困难无非就是：没兴趣、记不住、转不了弯。

使用“思维导图”的过程比传统死记硬背要主动且有趣得多，理清思路后又便于记忆，掌握原理后也减少难以融会贯通的问题。

“蓝橡树未来学校”针对1-3年级学生，订制了一个双12“思维导图探究课程礼包”，礼包包含有2节“思维导图课” 4节“社区探究主题课”，另外赠送2节“升学指导家长课”。

学生课程均为全英文外教授课！在2节思维导图课程中，学生将学到8种思维导图，这8张思维导图都是美国小学生最常使用的。

今天橡树君就根据课程内容总结这8种思维导图，如何使用？什么情况下用？一目了然。

（下文可能包含课程关键细节的透露）一、整理思路的利器：圆圈图（Circle Map）•常用指数：五颗星•使用场景：定义一件事情、展开一个主题等Circle Map是用于把一件主题，知识点，事物展开联想，或者描述细节。

它由一大一小两个圆圈构成，小圆圈里放的是你想要展开的主题，大圆圈里放的是和这个主题相关的细节和特征。

推理总结
先观察整体，后观察部分
九宫格或两组图
题型特征
每种样式的图形在行列中出现的次数相同，缺啥补啥
整体遍历
遍历（比较容易忽视）
每一组图都有一个相同的元素
局部遍历
规律特征
常在九宫格，相同样式图形在每个位置出现
位置遍历 图形、线条之间加减
加减
元素组成相似（样式规律）
两个图去掉相同部分，不同部分组成第三个图 两个图去掉不同部分，相同部分组成第三个图
去同存异 去异存同
运算
观察前两图的外边框，如外边框留下的线条多，先考虑求 同；如外边框留下的线条少，优先考虑求异。
技巧
6个图分组必考
题型特征
横、竖、斜
对称轴方向
对称轴数量
图形旋转180度得到的图形与原图相同
轴对称 中心对称
对称性
属性规律
经过处理的字母、汉字一般都是考虑对称性
技巧
曲线直线分开看 各自构成的图形分开看
三图对于列的黑块数相同
行列同时移动看
三图对应行和列的黑块数均不同
思路
上下左右
不动的黑块优先看
技巧
方向
有时黑块减少是因为移动后重叠
特征：黑块只在最外圈出现
确定时黑块，那就看中间隔的白块数量
技巧
每次走固定步数，一般是按照2，2，2的步数
如果是九宫格，注意观察两个黑块的相对位置，相对位置 保持不变
数量规律 面
规律技巧
相同元素，不看大小 元素之间数量的加减 元素之间的比例换算（比较难）
元素种类 元素个数
元素
扇形
多边形改造
特征
出现开口 角
直角、锐角、钝角的定义
注意：数角一般都是内角，不要数外角，而且不要重复

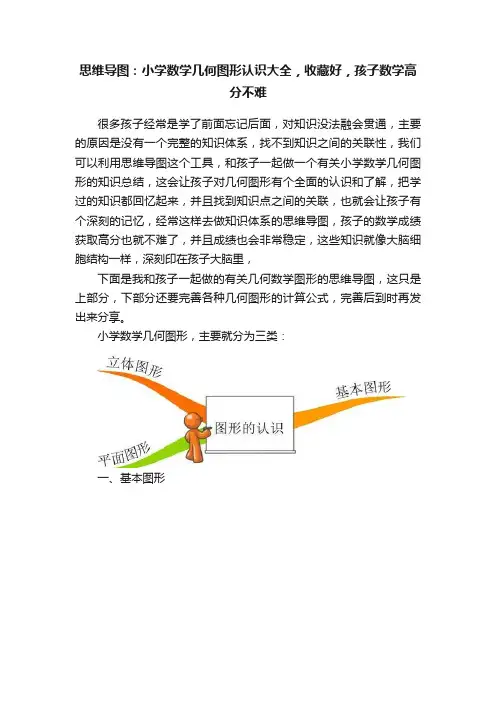
思维导图：小学数学几何图形认识大全，收藏好，孩子数学高分不难很多孩子经常是学了前面忘记后面，对知识没法融会贯通，主要的原因是没有一个完整的知识体系，找不到知识之间的关联性，我们可以利用思维导图这个工具，和孩子一起做一个有关小学数学几何图形的知识总结，这会让孩子对几何图形有个全面的认识和了解，把学过的知识都回忆起来，并且找到知识点之间的关联，也就会让孩子有个深刻的记忆，经常这样去做知识体系的思维导图，孩子的数学成绩获取高分也就不难了，并且成绩也会非常稳定，这些知识就像大脑细胞结构一样，深刻印在孩子大脑里，下面是我和孩子一起做的有关几何数学图形的思维导图，这只是上部分，下部分还要完善各种几何图形的计算公式，完善后到时再发出来分享。

小学数学几何图形，主要就分为三类：一、基本图形基本图形主要就是分为线和角。

线又分为：直线、射线、线段直线：线的两头无线延伸射线：一个端点，向另一端无线延伸线段：两个端点，不能超出两个端点距离：连接两点之间的线段长度，叫距离角可以分为：直角、钝角、锐角、平角、圆角对于角我们首先要了解角的表示方法，有边和顶点。

角的性质：角的大小是由两条边张开的程度决定，与边的长短无关。

直角：等于90º钝角：大于90º，小于180º锐角：小于90º平角：角的两条边成一条直线是180º圆角：是360º两条直线的位置关系：平行和相交二、平面图形平面图形分为圆、三角形、四边形圆：要了解原点、直径、半径的知识，是个轴对称图形三角形又可以分为：等腰三角形、等边三角形、直角三角形还有其它三角形。

对于三角形需要了解顶角、底角、底、腰、高这几个概念。

同时清楚等腰、等边、直角三角形的关系和构成。

等腰三角形：两腰相等，两底角相等等边三角形：三条边相等，三个角相等直角三角形：有一个角是直角当然除了这三种三角形，还有其它不规则的一些三角形。

四方形又可以分为平行四边形、长方形、正方形、梯形、菱形还有其它四边形。

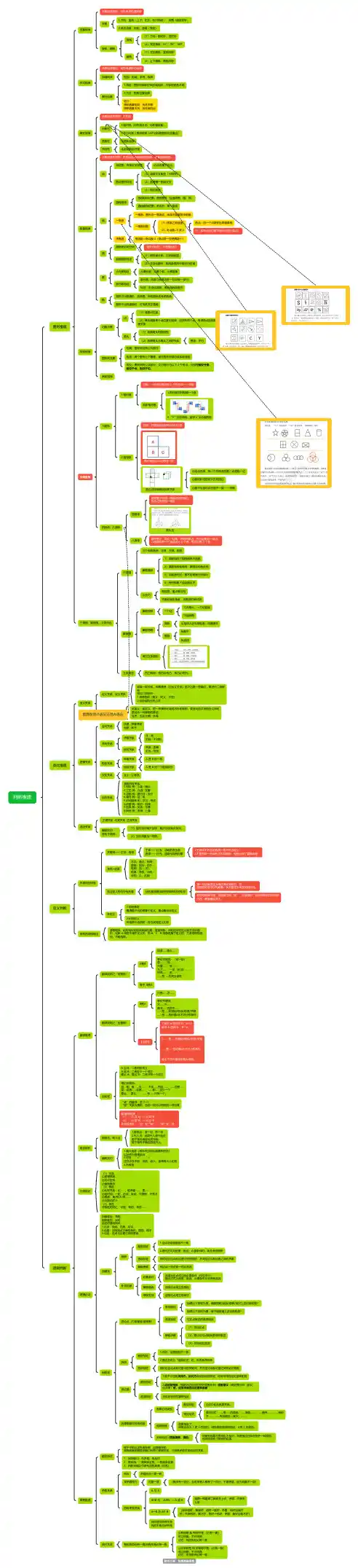
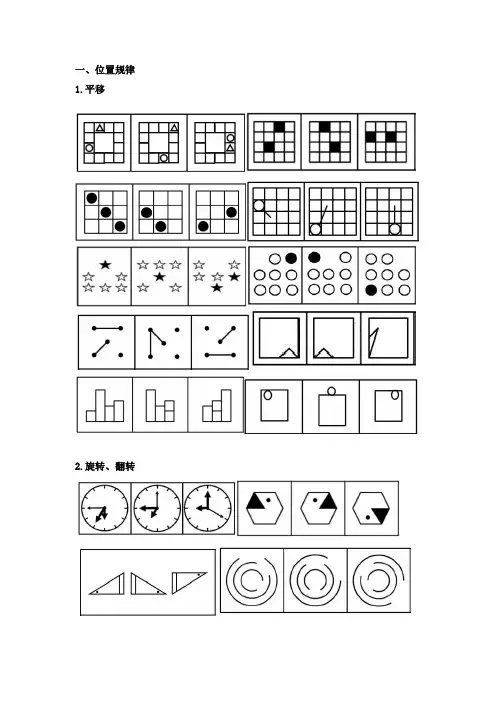
判断推理图形推理位置规律元素组成相同，优先考虑位置规律平移1.方向：直线（上下、左右、斜对角线）、绕圈（顺逆时针）2.常见步数：恒定、递增（等差）旋转、翻转旋转（1）方向：顺时针、逆时针（2）常见角度：45°、90°、180°翻转（1）左右翻转：竖轴对称（2）上下翻转：横轴对称样式规律元素组成相似，优先考虑样式规律加减同异相加、相减、求同、存异黑白运算1.特征：图形轮廓和分隔区域相同，内部的颜色不同2.方法：相同位置运算区分：黑块数量相同：优先平移黑块数量不同：优先黑白运属性规律元素组成不相同、不相似对称性1.轴对称（对称轴方向、对称轴数量）2.中心对称（图形旋转 180°后和原图形完全重合）曲直性全曲和全直开闭性全封闭和全开放数量规律元素组成不相同、不相似且观察属性无规律，数量规律明显。

点特征图：线条交叉明显切点也属于交点数点图形特征（1）线条交叉明显（大树杈）（2）乱糟糟一团线交叉（3）相切较多线直线曲线曲线数特征图：曲线图形（全曲线图、圆、弧）直线数特征图：多边形、单一直线一笔画一笔画：图形由一笔画成，线条不能重复来回画一笔画问题（1）线条之间连通（2）奇点数=0 或 2奇点：由一个点发射出奇数条线注：数奇点的时候不要忘记数上端点！多笔画笔画数=奇点数/2（奇点数一定是偶数个）面面就是封闭空间 面是白色的，不是黑色的！数面图形特征（1）图形被分割、封闭面明显（2）生活化图形、粗线条图形中留空白区域素小元素特征元素种类、元素个数、元素替换部分数特征部分数（线条与线条连在一起叫做一部分）特征：生活化图形、黑色粗线条图形角图形中出现扇形、改造图、折线图优先考虑数角图形中出现直角时，可优先关注直角特殊规律功能元素点（1）观察点位置（2）单独观察单个点位置无规律，且只有两个点，考虑两点连线和其他图形的位置关系箭头（1）观察箭头的指向性（2）观察箭头与箭头之间的关系垂直、平行图形间元素相离：图形间没有公共部分相压：两个图形上下覆盖，被压图形有部分线条被遮盖相交：图形间有公共部分，又可细分为以下 3 个考点，分别是相交于面、相交于点、相交于边。

创作编号：BG7531400019813488897SX创作者：别如克*思维导图，英文叫Mind Map，也称 Thinking Map ，就是借助图表来分析问题、理清思路。

今天介绍的都是思维图的基本款，体现了基础的思维框架。

但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用，可以变得非常复杂。

常见的思维图有这八种：Circle Map 圆圈图、Tree Map 树状图、Bubble Map 气泡图、Double Bubble Map 双重气泡图、Flow Map 流程图、Multi-flow Map 多重流程图、Brace Map 括号图，和Bridge Map 桥型图。

1、圆圈图，定义一件事（Circle Maps - Defining in Context ）Circle map 主要用于把一个主题展开来，联想或描述细节。

它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。

基本形状是这样的：下面是国外一个幼儿园孩子做的圆圈图练习。

左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。

而右边的图，反过来，从现象、特征（details）让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字，也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征（Bubble Maps -Describing Qualities ）国外很多幼儿园和小学都在用Bubble Map 来帮助孩子学习知识、描述事物，因为这个真的比较简单和管用，最基本的气泡图是这样的：圆圈图强调的是一个概念的具体展开，而气泡图，则更加侧重于对一个概念的特征描述。

比如这个孩子在用气泡图分析一只鹰有哪些特征。

看起来有点混，是不是？其实，檩子觉得，大家在实际带孩子分析问题的时候，不必太纠结到底该用哪种图，怎么直观怎么来，就行。

推理口诀：肯前必肯后，否后必否前，其余不一定
逆否等价：A→B＝-B→-A
翻译形式：B→A
后推前
特征词：1.只有A，才B 2.除非A，否则不B 3. 不A，不/勿/非B（主体要一致） 4.A是B的必要/必不可少的条件/基础/假设/前提/关键/重要（谁必不可少谁就放在 箭头的后面）
推理口诀：肯前必肯后，否后必否前，其余不一定
语法关系
1.主谓关系（学生：学习） 2.动宾关系（学习：功课） 3.主宾关系（学生：功课）
二级辨析：词语结构（大同小异）、感情色彩（褒义、贬义、中性）、词性（名 词、动词）、主客体是否一致（违章：罚款）
翻译形式：A→B，“否定词”用“—”
前推后
特征词：1.如果A，那么B 2.只要A，就B 3.倘若A，则B 4.凡是/所有A，都B 5.为了A，一定/必须B 6.A是/就/都/则B 7.如果/只要A，B 8.A是B的充分条件
加强削弱（注意主体是否一致）
否定论点
削弱题（反对 ） 力度：否定论点＞拆桥＞否定论据
拆桥 否定论据
因果论证、另有他因
话题一致原则
日常结论
选项绝对化要慎选，一般带有“可能”表述的选项才是正确答案
选项出现“比较”词语，那么题干也至少要出现两种情况才可以选
特征图：单条直线或曲线、端点、丁字口、五角星、日、圆、多个相交（相切）的 圆、与圆相交（相切）的线段或图形
笔画数
一笔画（能一笔画成的图形）
判断依据：图形之间线段连通且奇点数量＝0或2 奇点：由一个点发射出奇数条线，只看源头发出线的数量，与发出后的线是否连通 无关
多笔画（两笔画特征图：田）：笔画数＝奇点数/2，奇点一定是偶数个
行测
判断推理
定义判断（根据题干给出的定义，选出一个最符合或最不符合该定义的选项）

2、解分式方程
3、换元法解分式方程
4、分式方程的增根
5、分式方程的应用
第六章
平行四边形
平行四边形的性质
1、平行四边形的性质
2、等腰梯形的性质与判定
平行四边形的判定
平行四边形的判定与性质
三角形的中位线
三角形的中位线定理
多边形内角和与外角和
1、多边形的对角线
2、多边形内角和外角
第七章
平行线的证明
推理论证、命题定理
三角形
认识三角形
1、三角形的角平分线、中线和垂线
2、面积、重心、三边关系
3、内角和定理
4、外角性质
5、直角三角形的性质
图形的全等
1、全等图形
探索三角形全等的条件
1、三角形的稳定性
2、全等三角形的判定
3、全等三角形的判定与性质
尺规作图
尺规作三角形
全等三角形的应用
利用三角形全等测距离
第五章
生活中的轴对称
3、比较线段的长短
4、尺规作图
角
1、角的概念（钟面角、方向角）
2、度分秒的换算
3、作图--基本作图
角的比较
1、角平分线的定义
2、角的计算
3、角的大小的比较
多边形与圆的初步认识
1、多边形与多边形的对角线
2、圆的认识（圆心角、弧、弦的关系）
3、扇形面积的计算
第五章
一元一次方程
认识一元一次方程
1、方程的定义
推理论证、命题定理
平行线的判定
3、平行公理及推论
4、平行线的判定
平行线的性质
平行线的性质
三角形内角和定理
三角形内角和定理
九年级上册
第一章

目录
言语理解与表达思维导图 (3)
逻辑填空 (4)
概括类片段阅读——主旨理解题1 (5)
概括类片段阅读——主旨理解题2 (6)
细节类片段阅读 (7)
语句表达 (8)
篇章阅读 (9)
判断推理思维导图 (10)
图形推理——平面图形1 (11)
图形推理——平面图形2 (12)
图形推理——平面图形3 (13)
图形推理——空间重构 (14)
类比推理——横向辨析 (15)
类比推理——纵向辨析 (16)
定义判断 (17)
逻辑判断——基础知识1 (18)
逻辑判断——基础知识2 (19)
逻辑判断——形式逻辑1 (20)
逻辑判断——形式逻辑2 (21)
逻辑判断——论证逻辑1 (22)
逻辑判断——论证逻辑2 (23)
数量关系思维导图 (24)
数量关系——方法篇1 (25)
数量关系——方法篇2 (26)
数量关系——高频考点1 (28)
数量关系——高频考点3 (30)
数量关系——高频考点4 (31)
数量关系——高频考点5 (32)
数量关系——高频考点6 (33)
数量关系——高频考点7 (34)
资料分析思维导图 (36)
资料分析——速算技巧 (37)
资料分析——高频考点1 (38)
资料分析——高频考点2 (39)
资料分析——高频考点3 (40)
资料分析——高分必背 (41)
言语理解与表达思维导图
逻辑填空
细节类片段阅读
判断推理思维导图。

高中数学有难度？58页最全思维导图来袭，成绩提升不在话下
小器知道高中数学的知识点不仅涉及的范围广,而且难度大、逻辑性强,致使你们学习起来具有一定的困难,这时候就要求你们要具有的独立思考能力和逻辑思维能力，想要提升自己的学习效率,就要在学习过程中贯穿思维导图的应用，才是重要的突破口。

你们知道吗，通过实验研究,对在数学学习中运用思维导图进行积极的探索,应用思维导图学习可以很快地激发自己的学习兴趣、提升学习成绩也能更加发散自己的思维能力，这些都是具有很强的相关性的。

运用思维导图进行学习,以此为出发点,提高自己的数学成绩不再是梦想。

在同学们感到学习吃力，无论怎么努力分数都提不上来时，那么我就来分享一下由北大在读博士邱崇学长制作的，对高中数学所有的知识点做出的“高中数学全套的思维导图”免费分享给大家。

我真的希望能够帮助到更多因为数学而苦恼的小可爱！
还想要什么学习资料和各种学习方法，记得找我聊聊哦！
我是一点也不小气的小器～
上干货啦！
由于篇幅限制只能分享部分，想看高清完整版记得私信我哦！无偿分享！。