图形推理史上最全思维导图

一、位置规律 1.平移
2.旋转、翻转
二、样式规律 1.遍历
2.加减同异
3. 黑白运算
三、属性规律 1.对称性 轴对称图形（“等腰”元素）： 中心对称图形（字母“S”、“Z”、“N”、平行四边形）： 轴对称+中心对称图形： 2.曲直性 全直
全曲 有曲有直 3.开闭性 全开放：
全封闭： 半开半闭：
四、数量规律 1.点 （1）曲直交点
（2）框上、内交点 2.线 （1）直线
（2）曲线
（3）笔画数 “日”字及其变形图 “田”字及其变形图
“圆”相切或相交 多端点图 （4）平行线
3.角 4.面 （1）整体数面 （2）所有面的形状 （3）相.图形间关系 相离：
相交于点：
相交于线：
相交于面：
2. 功能元素 标记点： 标记线： 标记面： 标记角： 特殊功能元素：

特征法
总结词
根据图形的特征进行分类和比较的方法。
详细描述
特征法是解决图形推理问题的一种常用方法，需要考生根据图形的特征进行分类和比较，找出它们之间的相似性 和差异性。通过比较不同图形之间的特征，考生可以发现其中的规律和变化，从而推断出正确的答案。在应用特 征法时，考生需要特别注意图形的形状、结构、对称性等特征。
空间推理
总结词
根据二维图形推测三维图形的结构。
详细描述
空间推理是图形推理中的一种题型，它要求考生根据给出的二维图形，通过空间想象和 推理，推测出三维图形的结构。这种题型需要考生具备较强的空间想象能力和逻辑思维
能力。
组合推理
总结词
将多个图形按照一定的规则组合起来，形成 新的图形。
详细描述
组合推理是图形推理中的一种题型，它要求 考生根据题目给出的规则，将多个图形组合 起来，形成新的图形。这种题型需要考生对 图形的组合方式有较好的理解，能够根据规 则进行合理的组合。
02
图形推理的基本元素
点
点的大小
点是图形推理中最基本的元素，它没有大小，但有位置。在图形 推理中，点的位置、排列和数量可能成为解题的关键。
点与线的关系
点可以构成线，通过观察点与线的连接关系，可以推断出图形的变 化规律。
点与其他图形的组合
点与其他图形如线、面、立体等进行组合，可以形成复杂的图形结 构，增加了解题难度。
详细描述
假设法是解决图形推理问题的一种创造性方法，需要考生根 据题目要求和条件，提出假设条件，然后进行推理和验证。 在应用假设法时，考生需要特别注意假设条件的合理性和可 行性，以及推理过程的逻辑性和严密性。
04
图形推理的常见题型
类比推理

翻转的方向——左右翻转：竖轴对称，左右对调、上下不变。上下翻转： 横轴对称，上下对调、左右不变。 翻转 翻转的角度——180度旋转：上下左右对调 整体翻转——也整体（6个图）翻转/旋转形成新的图形
１
1.简单叠加，叠加后求同/求异（抓住1-2条线突破）；
叠加
2.位置变化（旋转/翻转）+求同/求异；行和列分别用不同的叠加规律。 ⚠要注意辨析：谁叠在谁的上面、谁被覆盖；区分部分叠加VS完全叠加、
优先考虑——切不出来的图形，用排除法。 六面体：六面体只能切出锐角三角形，切不出直角三角形、钝角三角形。 截面 圆柱：圆柱斜切得到弧线，不可能切出梯形。 图 ⚠️注意：空心没有实线；不同角度的截面无法共存，即刀不能拐弯切（eg. 不能外部横切矩形、同时内部斜切椭圆）；刀切过圆柱的弧面得到的是曲 线；关注切面的角（直角/锐角）；辨析实心和空心的颜色。
２
数量 规律
交点特征——有出头色彩，如十字形、T字型、L字型 曲直交点特征——图形均为类圆曲线，圆和弧线多且曲直相交 切点特征——类圆曲线+点连接 圆内交点——每幅图都仅有一个圆，线条贯穿圆内外 点 其他考点——曲曲/直直交点数（和/差），内外交点（图形均有外框，内 外分开看：内部交点、外部交点、内外交点的和/差），黑点/白点连接形 成的部分数，线条经过或覆盖的点的数量，点在四个角的位置移动，相连 黑圆圈的数量变化（eg.各行分别有1、2、3个黑圆相连）
３
属性 规律
对称的考点主要有：对称方式，对称轴数量/方向，对称轴两侧空间的形 状，对称轴经过的点/线/面的数量。 1.轴对称——提示点：等腰三角形/梯形、箭头及其变形、五角星、一边一 个相同元素（如Y）。 具体考点——对称轴的方向/数量，对称轴与图形中某点/某线的关系（对 称轴经过交点/直线/与线重合），对称轴的自身的角度，对称轴旋转的角 度，字母和汉字要注意书写笔画长短/大小是否严格符合对称性，对称轴是 对称 否经过所有面，最大/最小面的对称性，两个对称图形要考虑对称轴之间的 关系。 2.中心对称——旋转180度后完全重合；两个相同图形反着放。提示点：平 行四边形，S、N、Z字型，风车及其变形。 3.轴+中心对称——存在两条互相垂直的对称轴。 4.整体对称：图形米字型整体对称，五个图以第三个图为轴成轴对称，白块 /黑块的整体对称性，对称轴的数量对称（如对称轴数量分别为 4/1/2/2/1/4）。

一般递增或递减是按照1，2，3，4的顺序
步数恒定的 步数有序加减的
步数
平移（黑白块问题）
一般都是循环的，但也要注意来回弹着跑的
路径
顺时针 逆时针
方向
45度，60度，90度，120度，135度，180度
旋转角度
旋转
元素组成相同（位置规律）
上下翻转，左右不变 左右翻转，上下不变
翻转
不动的部分优先看
注意比较选项差异
三图对于列的黑块数相同
行列同时移动看
三图对应行和列的黑块数均不同
思路
上下左右
不动的黑块优先看
技巧
方向
有时黑块减少是因为移动后重叠
特征：黑块只在最外圈出现
确定时针移动的方向，区分不同的黑块
思路
顺逆时针
如果只有两个黑块，那就看中间隔的白块数量
技巧
每次走固定步数，一般是按照2，2，2的步数
如果是九宫格，注意观察两个黑块的相对位置，相对位置 保持不变
原来被遮挡的看不到
先观察图形，能第一眼看出结论即选
第一眼看不出结论，去观察选项 勾出特殊或不同的图去进行比较
关于分组
图形推理
两个相对面同时出现，排除 两个相对面同时都没出现，排除
相对面
空间重构
公共边不变
相邻面
圆柱：上下切 六面体：上下、斜、拦腰切
圆锥：沿着顶点向下切 六面体：沿着棱上某一点斜切
截面有矩形
截面有三角形
截面图
空间类
立体图形本身有弧线则拦腰或斜切均可以 主视、俯视、左视
截面有弧线 三个角度
剖面图
原来有线才有线
三视图
推理总结
先观察整体，后观察部分

黑+黑、白+白、黑+白
轴对称（％不是轴对称图形）
数量：对称轴的总数、横向对称轴的数量、竖向对称轴的数量 位置：对称轴的角度变化（45°、90°、180°）、各个图形间对称轴平行或垂直或相 交、都是横向对称轴或者竖向对称轴、对称轴过交点或对称轴过边
图形推理
组成元素不同：属性规律
考点
对称性（只要有一个图形不是轴对称或者中心对称就不用考虑对称性）
元素个数（所有素的总数、各个素之间的数量关系：211）
元素替换（从第二和第三个图形破题）
数部份（线段连在一起的叫一部分）
特征图：生活化图形、黑粗线条图形、5×5及以上规格的黑白小方块或小球的组合 图
特征图：锐角、直角、钝角、三角形图、折线图、扇形图、缺口缺角的改造图
角规律（指0°~180°的角）
数量：直角、锐角、钝角的个数（出现直角时优先关注） 角度数的变化：0°-45°-90°-135°-180°
相交：面与面相交于点、面、长边、短边、面与面包含、交错 相压：面与面相压（注意相压面的大小和相压的顺序） 相离：面与面相离
相对面：展开图中，同行或同列中间隔一个面的面、紧邻Z字中线两端的面 （一个立体图形只能同时看到一个相对面）
六面体（先用相对面排除，然后找有指向性图形的面，不行再用画边法）
相邻面：展开图中，构成直角的两条边是同一条边，这两条边所在的面就是相邻面 指向性：找有指向性图形的面，结合相邻面规律排除选项
展开图
画边法(找到唯一的特殊点或特殊边顺时针画边)
四面体：展开图中，构成一条直线的两条边是同一条边，这条直线所在的面就是相 邻面
八面体：展开图中，构成“开口钝角”的两条边是同一条边；每个点都只能连接四 个面

推理总结
先观察整体，后观察部分
九宫格或两组图
题型特征
每种样式的图形在行列中出现的次数相同，缺啥补啥
整体遍历
遍历（比较容易忽视）
每一组图都有一个相同的元素
局部遍历
规律特征
常在九宫格，相同样式图形在每个位置出现
位置遍历 图形、线条之间加减
加减
元素组成相似（样式规律）
两个图去掉相同部分，不同部分组成第三个图 两个图去掉不同部分，相同部分组成第三个图
去同存异 去异存同
运算
观察前两图的外边框，如外边框留下的线条多，先考虑求 同；如外边框留下的线条少，优先考虑求异。
技巧
6个图分组必考
题型特征
横、竖、斜
对称轴方向
对称轴数量
图形旋转180度得到的图形与原图相同
轴对称 中心对称
对称性
属性规律
经过处理的字母、汉字一般都是考虑对称性
技巧
曲线直线分开看 各自构成的图形分开看
三图对于列的黑块数相同
行列同时移动看
三图对应行和列的黑块数均不同
思路
上下左右
不动的黑块优先看
技巧
方向
有时黑块减少是因为移动后重叠
特征：黑块只在最外圈出现
确定时黑块，那就看中间隔的白块数量
技巧
每次走固定步数，一般是按照2，2，2的步数
如果是九宫格，注意观察两个黑块的相对位置，相对位置 保持不变
数量规律 面
规律技巧
相同元素，不看大小 元素之间数量的加减 元素之间的比例换算（比较难）
元素种类 元素个数
元素
扇形
多边形改造
特征
出现开口 角
直角、锐角、钝角的定义
注意：数角一般都是内角，不要数外角，而且不要重复

公务员考试图形推理解题50项思路1.大小变化2.方向旋转3.笔画增减(数字,线条数)4.图形求同5.相同部份去掉6.图形叠加(简单叠加,合并叠加,去同叠加)7.图形组合变化(如:首尾两个图形中都包含中间图形)8.对应位置阴影变化(两图相同或不同则第三图对应位置变阴影或变空白)9.顺时针或逆时针旋转10.总笔画成等差数列11.由内向外逐步包含12.相同部件,上下,左右组合13.类似组合(如平行,图形个数一样等)14.横竖线条之比有规律(如横线3条竖线4条,横线4条竖线5条等)15.缺口相似或变化趋势相似（如逐步远离或靠近）16.图形运动变化(同一个图形从各个角度看的不同样子)17.图形拆分(有三个图构成,后两个图为第一个图的构成部件)18.线条交点数有规律19.方向规律(上,下,左,右)20.相隔一个图形分别对称(如:以第三个图为中心,1和5对称,2和4对称)21.含义依据条件而变(如一个错号,可以表"划",也可以表示"两划")22.图形趋势明显(点或图形从左到右,从上到下变化等)23.图形的上,中,下部分分别变化(求同,重叠,或去同叠加)24.相似类(包含,平行,覆盖，相交，不同图形组成，含同一图形等）25.上,中,下各部分别翻转变化26.角的度数有规律27.阴影重合变空白28.翻转,叠加,再翻转30.与特定线的交点数相同(如:与折线的交点数有规律,有直线的交点数不用考虑)31.图形有多条对称轴,且有共同交点,轴对称图形(如正三角形,正方形)32.平行,上下移动33.图形翻转对称34.图形边上角的个数增多或减少35.不同图形叠加形成新图36.图形中某条线均为长线或短线(寻找共同部分)37.线段间距离共性.(如:直线上有几个点,分成几条线段,上部覆盖有另一个图形，如圆，三角形等，但是上面的图形占的位置都不大于最外面两点间的距离）38.图形外围,内部分别顺或逆时针旋转(内外部变化相反)39.特殊位置变化有规律(如当水平时,垂直时图形有一规律）40.各图形组成部件属于同一类(如:均为三条曲线相交)41.以第几幅图为中心进行变化(如:旋转,走近,相反等)42.求共同部分再加点变化(如:提出共同部分,然后让共同部分都变黑什么的)43.除去共同部分有规律44.数线段出头数,有规律(成等差数列,或有明显规律)45.图形每行空间数相同46.以中间图形为中心,上下,对角分别成对称47.先递增再递减规律48.整套图形横着看,或竖着看,分别有规律.49.注意考虑图形部分变化(如:分别为上下不变中间变化,然后上中下一起变化,左右分别变化,左右一起变化等)50.顺着次序变化．（如:原来在内部的放大变为外部图形,内部图形相应变化.左右组成的图,上一个右边图等于下个左边图,右边再加个新图,如此循环)1.大小变化2.方向旋转3.笔画增减(数字,线条数)4.图形求同5.相同部份去掉6.图形叠加(简单叠加,合并叠加,去同叠加)7.图形组合变化(如:首尾两个图形中都包含中间图形)8.对应位置阴影变化(两图相同或不同则第三图对应位置变阴影或变空白)9.顺时针或逆时针旋转10.总笔画成等差数列11.由内向外逐步包含12.相同部件,上下,左右组合13.类似组合(如平行,图形个数一样等)14.横竖线条之比有规律(如横线3条竖线4条,横线4条竖线5条等)15.缺口相似或变化趋势相似（如逐步远离或靠近）16.图形运动变化(同一个图形从各个角度看的不同样子)17.图形拆分(有三个图构成,后两个图为第一个图的构成部件)18.线条交点数有规律19.方向规律(上,下,左,右)20.相隔一个图形分别对称(如:以第三个图为中心,1和5对称,2和4对称)21.含义依据条件而变(如一个错号,可以表"划",也可以表示"两划")22.图形趋势明显(点或图形从左到右,从上到下变化等)23.图形的上,中,下部分分别变化24.相似类(包含,平行,覆盖，相交，不同图形组成，含同一图形等）25.上,中,下各部分别翻转变化26.角的度数有规律27.阴影重合变空白28.翻转,叠加,再翻转30.与特定线的交点数相同(如:与折线的交点数有规律,有直线的交点数不用考虑)31.图形有多条对称轴,且有共同交点,轴对称图形(如正三角形,正方形)32.平行,上下移动32.平行,上下移动33.图形翻转对称34.图形边上角的个数增多或减少35.不同图形叠加形成新图36.图形中某条线均为长线或短线(寻找共同部分)37.线段间距离共性.(如:直线上有几个点,分成几条线段,上部覆盖有另一个图形，如圆，三角形等，但是上面的图形占的位置都不大于最外面两点间的距离）38.图形外围,内部分别顺或逆时针旋转(内外部变化相反)39.特殊位置变化有规律(如当水平时,垂直时图形有一规律）40.各图形组成部件属于同一类(如:均为三条曲线相交)41.以第几幅图为中心进行变化(如:旋转,走近,相反等)42.求共同部分再加点变化(如:提出共同部分,然后让共同部分都变黑什么的)43.除去共同部分有规律44.数线段出头数,有规律(成等差数列,或有明显规律)45.图形每行空间数相同46.以中间图形为中心,上下,对角分别成对称47.先递增再递减规律48.整套图形横着看,或竖着看,分别有规律.49.注意考虑图形部分变化(如:分别为上下不变中间变化,然后上中下一起变化,左右分别变化,左右一起变化等)50.顺着次序变化．（如:原来在内部的放大变为外部图形,内部图形相应变化.左右组成的图,上一个右边图等于下个左边图,右边再加个新图,如此循环)几乎概括了图形推理的所有类型,大家帮顶啊,传图片好费劲啊图片：图片：图片：图片：图片：图片：图片：图片：图片：[attachment=115459] 看看哦,希望对你有帮助!!。

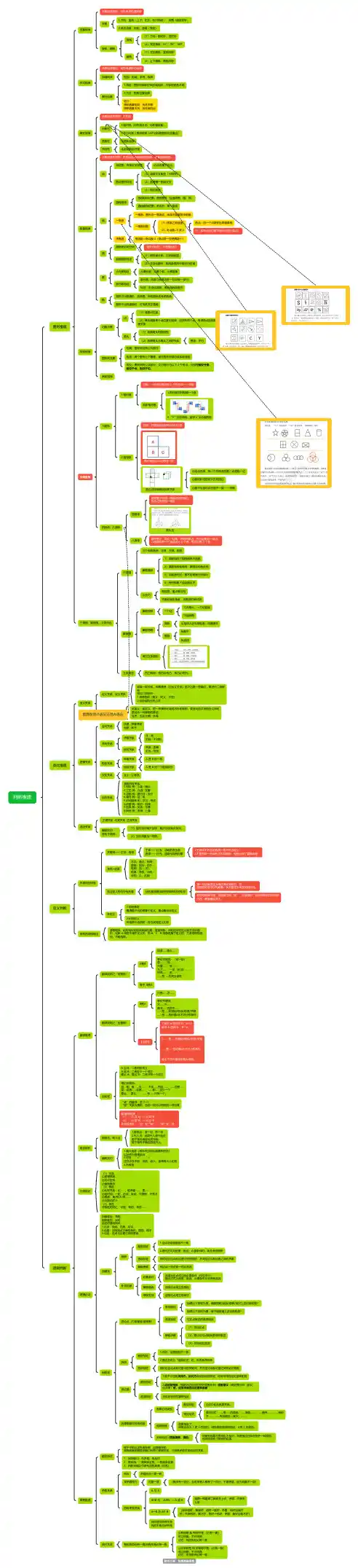
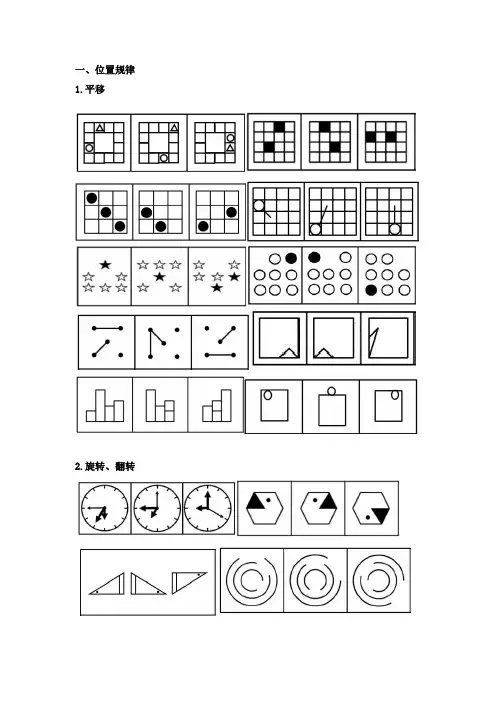
判断推理图形推理位置规律元素组成相同，优先考虑位置规律平移1.方向：直线（上下、左右、斜对角线）、绕圈（顺逆时针）2.常见步数：恒定、递增（等差）旋转、翻转旋转（1）方向：顺时针、逆时针（2）常见角度：45°、90°、180°翻转（1）左右翻转：竖轴对称（2）上下翻转：横轴对称样式规律元素组成相似，优先考虑样式规律加减同异相加、相减、求同、存异黑白运算1.特征：图形轮廓和分隔区域相同，内部的颜色不同2.方法：相同位置运算区分：黑块数量相同：优先平移黑块数量不同：优先黑白运属性规律元素组成不相同、不相似对称性1.轴对称（对称轴方向、对称轴数量）2.中心对称（图形旋转 180°后和原图形完全重合）曲直性全曲和全直开闭性全封闭和全开放数量规律元素组成不相同、不相似且观察属性无规律，数量规律明显。

点特征图：线条交叉明显切点也属于交点数点图形特征（1）线条交叉明显（大树杈）（2）乱糟糟一团线交叉（3）相切较多线直线曲线曲线数特征图：曲线图形（全曲线图、圆、弧）直线数特征图：多边形、单一直线一笔画一笔画：图形由一笔画成，线条不能重复来回画一笔画问题（1）线条之间连通（2）奇点数=0 或 2奇点：由一个点发射出奇数条线注：数奇点的时候不要忘记数上端点！多笔画笔画数=奇点数/2（奇点数一定是偶数个）面面就是封闭空间 面是白色的，不是黑色的！数面图形特征（1）图形被分割、封闭面明显（2）生活化图形、粗线条图形中留空白区域素小元素特征元素种类、元素个数、元素替换部分数特征部分数（线条与线条连在一起叫做一部分）特征：生活化图形、黑色粗线条图形角图形中出现扇形、改造图、折线图优先考虑数角图形中出现直角时，可优先关注直角特殊规律功能元素点（1）观察点位置（2）单独观察单个点位置无规律，且只有两个点，考虑两点连线和其他图形的位置关系箭头（1）观察箭头的指向性（2）观察箭头与箭头之间的关系垂直、平行图形间元素相离：图形间没有公共部分相压：两个图形上下覆盖，被压图形有部分线条被遮盖相交：图形间有公共部分，又可细分为以下 3 个考点，分别是相交于面、相交于点、相交于边。

23／59
请关注微信公众号“名师伴你学”获取更多精品资源
24／59
请关注微信公众号“名师伴你学”获取更多精品资源
25／59
请关注微信公众号“名师伴你学”获取更多精品资源
26／59
请关注微信公众号“名师伴你学”获取更多精品资源
27／59
请关注微信公众号“名师伴你学”获取更多精品资源
28／59
56／59
请关注微信公众号“名师伴你学”获取更多精品资源
57／59
请关注微信公众号“名师伴你学”获取更多精品资源
58／59
请关注微信公众号“名师伴你学”获取更多精品资源
59／59
请关注微信公众号“名师伴你学”获取更多精品资源
29／59
请关注微信公众号“名师伴你学”获取更多精品资源
30／59
请关注微信公众号“名师伴你学”获取更多精品资源
31／59
请关注微信公众号“名师伴你学”获取更多精品资源
32／59
请关注微信公众号“名师伴你学”获取更多精品资源
33／59
请关注微信公众号“名师伴你学”获取更多精品资源
6／59
请关注微信公众号“名师伴你学”获取更多精品资源
7／59
请关注微信公众号“名师伴你学”获取更多精品资源
8／59
请关注微信公众号“名师伴你学”获取更多精品资源
9／59
请关注微信公众号“名师伴你学”获取更多精品资源
10／59
请关注微信公众号“名师伴你学”获取更多精品资源
11／59
请关注微信公众号“名师伴你学”获取更多精品资源
请关注微信公众号“名师伴你学”获取更多精品资源
18／59
请关注微信公众号“名师伴你学”获取更多精品资源

公务员行测考试：图推解题技巧和思路讲解全覆盖(史上最全) 鲤鱼网()35。

不同的图被叠加以形成新的图36。

图中的一条线可以是一条长线，也可以是一条短线(寻找公共部分)37。

线段之间的距离共性。

(例如，一条直线上有几个点，分成几个线段，而上面部分覆盖着另一个图形，如圆、三角形等。

但是，上述数字所占的位置并不比最外面两点之间的距离大多少)鲤鱼网()38。

图的外围，内部分别顺时针或逆时针旋转(内部和外部反向变化) 39。

特殊位置有规律地变化(如当水平时，在垂直图形中有一个规则)40。

图形的每个组成部分都属于同一类别(例如，所有三条曲线相交)41。

改变以哪个图形为中心(例如，旋转、接近、相反等)。

)鲤鱼网()42。

寻找共同的部分并添加一些变化(例如，提出共同的部分，然后使共同的部分变成黑色或类似的东西)43。

去掉常见零件，有常规44。

线段数量有规律(成等差数列，或有明显规律)45。

图中每一行的空格数是相同的鲤鱼网()46。

以中间的图形为中心，向上和向下，对角分别对称47°。

先增后减的规律是48。

当水平或垂直观察时，整套图形是规则的。

49。

应注意图形部分的变化(如中间变化从上到下分别不变，然后上、中、下部分一起变化，左、右部分分别变化，左、右部分一起变化等)。

)鲤鱼网()50。

根据顺序改变。

(例如，原来的内部放大变成了外部图形，内部图形也相应地改变。

对于由左、右部分组成的图形，前一个右图形等于下一个左图形，新图形添加到右侧。

这个循环)几乎总结了所有类型的图形推理，大家都帮着顶，很难转移图片鲤鱼网()第一部分，数值推理1，基本要求熟悉常见序列，保持数字的敏感性，同时注意逆序自然数平方系列:4，1，0，1，4，9，16，25，36，49，64，81，100，121，169，196，225，256，289，324，361，400...自然数立方级数:-8，-1，0，1，8，27，64，125，216，343，512，729，1000素数序列:2，3，5，7，11，13，17...(注意逆序，例如17，13，11，7，5，3，2)复合数字序列:4，6，8，9，10，12，14....(注意相反顺序)2。

数学几何图形概念思维导图几何是研究空间和形状的数学分支。

在几何中，图形是最基本的概念之一。

图形是由一组点和它们之间的连接线组成的。

在数学中，几何图形可以通过概念思维导图来清晰地展示和总结。

概念思维导图是一种以图形化方式展示信息和构建关联的工具。

它通过将主题和子主题以及它们之间的关系用图形表示出来，帮助我们更好地理解和记忆知识内容。

下面是一个数学几何图形概念思维导图的示例：(图片描述：概念思维导图)圆形是一个基本概念，它由一个具有相同半径的圆心和一条半径组成。

圆形在几何中非常常见，它具有许多重要的性质。

其中一些性质包括：1. 直径：直径是通过圆心的任意两点的线段，它的长度等于圆的半径的两倍。

2. 弧：弧是圆的一部分，它由一个起点、一个终点和一个连接这两点的曲线组成。

3. 弧长：弧长是圆上的弧的实际长度。

它可以通过圆的周长和圆心角的度数来计算。

4. 正切：正切是从圆心到圆上某个点的直线与半径的比值。

在三角函教程中，正切是一个重要的概念。

接下来，我们来看看另一个常见的几何图形——矩形。

矩形是一个有四个直角的平面图形。

它有一些重要的性质，如：1. 面积：矩形的面积等于其长度乘以宽度。

2. 对角线：矩形的对角线是连接相对顶点的线段，它们相等且交于中点。

3. 周长：矩形的周长是所有边长的和。

除了圆形和矩形之外，还有许多其他几何图形的重要概念需要我们掌握。

例如三角形、正方形、梯形等等。

每个图形都有其独特的性质和公式，通过概念思维导图，我们可以有效地组织和记忆这些知识。

几何图形的理解对于解决实际问题和应用数学知识至关重要。

无论是在建筑设计、地理测量还是计算机图形学等领域，几何都扮演着重要角色。

因此，我们应该努力学习和掌握几何图形的概念和性质。

通过本文的思维导图，我们可以清晰地了解和回顾数学几何图形的相关概念。

希望这个思维导图能帮助你更好地理解和应用几何知识，提高数学学习的效果。

让我们一起努力，探索数学的美妙世界！。

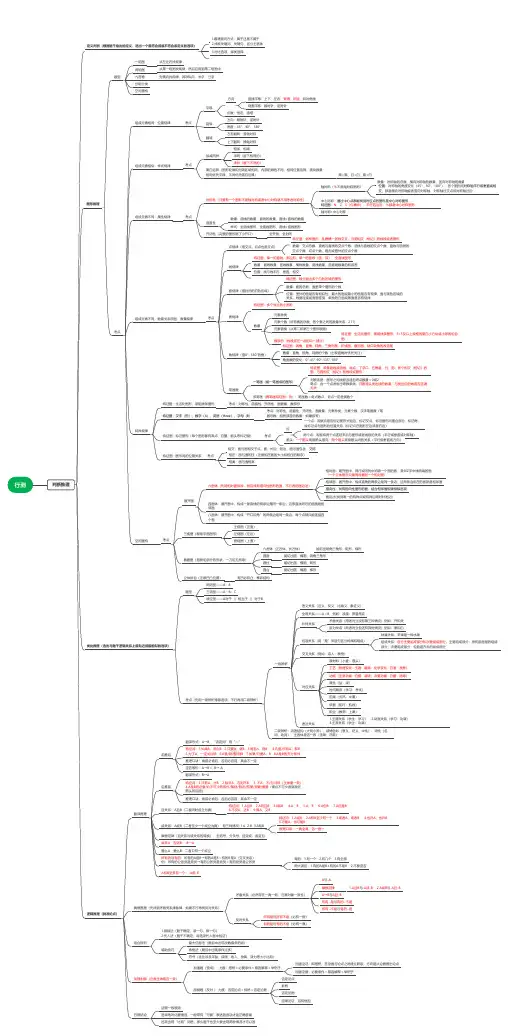
重磅初中数学思维导图全汇总收藏(word版可编辑修改)
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（重磅初中数学思维导图全汇总收藏(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为重磅初中数学思维导图全汇总收藏(word版可编辑修改)的全部内容。

重磅!!初中数学思维导图全汇总｜收藏数学
以微课堂
“数与代数"部分
以微课堂
“空间与图形”部分
“统计与概率”部分
以微课堂
“实践与应用”部分
将以上四块内容进一步细分，可得到以下各个部分。

以微课堂
1、代数式
以微课堂
2、一次函数与反比例函数
以微课堂
3、二次函数与一元二次方程
以微课堂
4、图形认识、相交线与平行线
以微课堂5、三角形
以微课堂
6、四边形与圆
以微课堂
7、图形的全等变换
以微课堂
8、全等三角形与相似三角形
以微课堂
9、统计与概率。

一张思维导图，就能让孩子逻辑思维更强大！火星的妈妈2016-08-30 10:05每个妈妈都希望自己的孩子是个表达能力强的小能人，最好还有逻辑清晰、聪明伶俐、人见人爱等光环加持。

在培养孩子的表达能力方面，大多数妈妈无师自通，天生就会开发自己孩子的语言天分：先教孩子一些简单的常用词汇，然后再逐渐培养孩子连成简单的句子，慢慢的孩子会在与各种不同的人沟通过程中说出越来越多的句子，直到变成完整的一段话。

为宝宝们鼓掌！那么你知道怎样培养孩子的逻辑思维能力吗？举个例子。

Tom小朋友想要办个生日party，在他的脑海中为了办好自己的生日爬梯产生了很多想法，不会写字的他在纸上画了下来：首先要知道自己的生日是哪一天（以便通知朋友们那一天来呀）；然后生日这天他决定邀请三个好朋友分享他的快乐(很好，人数定下来，妈妈就知道准备多少菜肴了)；接着，他想在温馨的家里庆祝生日，生日前要用彩链、气球、星星来装饰一下客厅（下图3、4中内容）；他还想准备许多好吃的好玩的：巧克力、蛋糕、芭比娃娃、国际象棋、画画板（真是个有模有样的小主人）；生日结束他还想送好朋友每人一件礼物（啧啧，有贴心暖男潜质）。

看到这里你一定感叹，好聪明的孩子，还不会写字，逻辑就已经形成了！其实，这位小Tom用图形表达逻辑想法的方式叫做画思维导图（Thinking Map）。

思维导图是世界著名的英国学者TONY BUZAN 在1970发明的一种表达发散性思维的的有效图形思维工具，把我们大脑中的想法用彩色的笔画在纸上。

它运用图文并重的技巧将左脑的逻辑、顺序、条例、文字、数字，以及右脑的图像、想象、颜色、空间、整体思维等各种因素全部调动起来，充分运用左右脑的机能，开启我们大脑的无限潜能。

再举个例子。

一位想吃苹果派的小朋友，通过观察和思考，追根思源到一颗苹果种子，于是画了下面的思维导图。

不得不感叹，会画思维导图的孩子简直是赢在了逻辑的起跑线上！宝爸宝妈们一定也希望自己的孩子能拥有这样清晰的逻辑吧~那么问题来了：如何让孩子掌握画思维导图的方法呢？1、拿出一张白纸，鼓励孩子将思考主题写在纸中央鼓励孩子头脑中冒出的每一个想法，让他画或者写在白纸中央。