电磁场与电磁波第一章复习

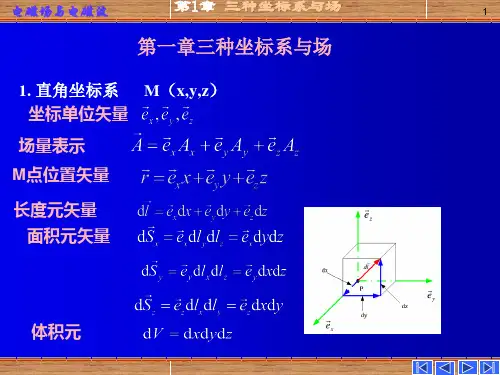
电磁场与电磁波复习第一部分 知识点归纳 第一章 矢量分析1、三种常用的坐标系 （1）直角坐标系微分线元：dz a dy a dx a R d z y x →→→→++= 面积元：⎪⎩⎪⎨⎧===dxdy dS dxdz dS dydzdS zyx ，体积元：dxdydz d =τ（2）柱坐标系长度元：⎪⎩⎪⎨⎧===dz dl rd dl drdl z r ϕϕ，面积元⎪⎩⎪⎨⎧======rdrdzdl dl dS drdz dl dl dS dz rd dl dl dS z zz r z r ϕϕϕϕ，体积元：dz rdrd d ϕτ=（3）球坐标系长度元：⎪⎩⎪⎨⎧===ϕθθϕθd r dl rd dl drdl r sin ，面积元：⎪⎩⎪⎨⎧======θϕθϕθθθϕϕθθϕrdrd dl dl dS drd r dl dl dS d d r dl dl dS r r r sin sin 2，体积元：ϕθθτd drd r d sin 2=2、三种坐标系的坐标变量之间的关系 （1）直角坐标系与柱坐标系的关系⎪⎪⎩⎪⎪⎨⎧==+=⎪⎩⎪⎨⎧===z z x y yx r z z r y r x arctan,sin cos 22ϕϕϕ （2）直角坐标系与球坐标系的关系⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=⎪⎩⎪⎨⎧===z yz y x z z y x r r z r y r x arctan arccos ,cos sin sin cos sin 222222ϕθθϕθϕθ （3）柱坐标系与球坐标系的关系⎪⎪⎩⎪⎪⎨⎧=+=+=⎪⎩⎪⎨⎧===ϕϕθθϕϕθ22'22''arccos ,cos sin z r z zr r r z r r 3、梯度（1）直角坐标系中：za y a x a grad z y x ∂∂+∂∂+∂∂=∇=→→→μμμμμ（2）柱坐标系中：za r a r a grad z r ∂∂+∂∂+∂∂=∇=→→→μϕμμμμϕ1（3）球坐标系中：ϕμθθμμμμϕθ∂∂+∂∂+∂∂=∇=→→→sin 11r a r a r a grad r4.散度（1）直角坐标系中：zA y A x A A div zy X ∂∂+∂∂+∂∂=→（2）柱坐标系中：zA A r rA r r A div zr ∂∂+∂∂+∂∂=→ϕϕ1)(1 （3）球坐标系中：ϕθθθθϕθ∂∂+∂∂+∂∂=→A r A r A r rr A div r sin 1)(sin sin 1)(122 5、高斯散度定理：⎰⎰⎰→→→→=⋅∇=⋅ττττd A div d A S d A S，意义为：任意矢量场→A 的散度在场中任意体积内的体积分等于矢量场→A 在限定该体积的闭合面上的通量。

电子信息学院电磁场与电磁波第一章复习题练习姓名学号班级分数1-7题，每题5分；8-15题，每题5分，16题10分，17题15分。

8:解：不总等于，讨论合理即可9. 已知直角坐标系中的点P1(-3，1，4)和P2（2，-2,3）：(1)在直角坐标系中写出点P1、P2的位置矢量r1和r2；(2)求点P1到P2的距离矢量的大小和方向；(3)求矢量r1在r2的投影；解：（1）r1=-3a x+a y+4a z;r2=2a x-2a y+3a z(2)R=5a x-3a y-a z(3) [（r1•r2）/ │r2│] =（17）½10.用球坐标表示的场E=a r 25/r2，求：（1）在直角坐标系中的点（-3,4，-5）处的|E|和E z；（2）E与矢量B=2a x-2a y+a z之间的夹角。

解：（1）0.5；2½/4;(2)153.611.试计算∮s r·d S的值，式中的闭合曲面S是以原点为顶点的单位立方体，r为空间任一点的位置矢量。

解：学习指导书第13页12.从P（0,0,0）到Q（1,1,0）计算∫cA·d l，其中矢量场A的表达式为A=ax 4x-ay14y2.曲线C沿下列路径：（1） x=t，y=t2；（2）从（0,0,0）沿x轴到（1,0,0），再沿x=1到（1,1,0）；（3）此矢量场为保守场吗？解：学习指导书第14页13.求矢量场A =a x yz+a y xz+a z xy 的旋度。

A ∇⨯=x a （x -x ）+y a （y -y ）+z a （z -z ）=0 14.求标量场u=4x 2y+y 2z-4xz 的梯度。

u ∇=x a u x ∂∂+y a u y ∂∂+z a u z ∂∂=x a (8xy-4z)+y a (42x +2yz)+z a (2y -4x)15.求矢量场A =a x x 2y+a y yz+a z 3z 2在点P （1,1,0）的散度。

梯度: 高斯定理:A d S ，电磁场与电磁波知识点要求第一章矢量分析和场论基础1理解标量场与矢量场的概念；场是描述物理量在空间区域的分布和变化规律的函数。

2、理解矢量场的散度和旋度、标量场的梯度的概念，熟练掌握散度、旋度和梯度的计算公 式和方法(限直角坐标系)。

:u；u；u e xe ye z ，-X；y: z物理意义：梯度的方向是标量u 随空间坐标变化最快的方向;梯度的大小：表示标量 u 的空间变化率的最大值。

散度：单位空间体积中的的通量源，有时也简称为源通量密度,旋度：其数值为某点的环流量面密度的最大值， 其方向为取得环量密度最大值时面积元的法 线方向。

斯托克斯定理：■ ■(S?AdS|L )A d l数学恒等式：' Cu )=o ,「c A )=o3、理解亥姆霍兹定理的重要意义：a时，n =3600/ a , n为整数，则需镜像电荷XY平面, r r r.S(—x,y ,z)-q ■严S(-x , -y ,z)S(x F q R 1qS(x；-y ,z )P(x,y,z)若矢量场A在无限空间中处处单值，且其导数连续有界，源分布在有限区域中，则矢量场由其散度和旋度唯一地确定，并且矢量场A可表示为一个标量函数的梯度和一个矢量函数的旋度之和。

A八F u第二、三、四章电磁场基本理论Q1、理解静电场与电位的关系，u= .E d l，E(r)=-V u(r)P2、理解静电场的通量和散度的意义，「s D d S「V "v dV \ D=，VE d l 二0 ' ' E= 0静电场是有散无旋场，电荷分布是静电场的散度源。

3、理解静电场边值问题的唯一性定理，能用平面镜像法解简单问题;唯一性定理表明：对任意的静电场，当电荷分布和求解区域边界上的边界条件确定时，空间区域的场分布就唯一地确定的镜像法：利用唯一性定理解静电场的间接方法。

关键在于在求解区域之外寻找虚拟电荷，使求解区域内的实际电荷与虚拟电荷共同产生的场满足实际边界上复杂的电荷分布或电位边界条件，又能满足求解区域内的微分方程。

第一章矢量分析①A A Ae =②cos A B A Bθ⋅=⋅③A 在B 上的分量B AB A B A COS BA θ⋅==④e xyz x y z xyzA B e e A A AB B B⨯=⑤A B A B⨯=-⨯ ,()A B C A B A C⨯+=⨯+⨯ ,()()()A B C B C A C A B ⋅⨯=⋅⨯=⋅⨯(标量三重积)，()()()A B C B A C C A B ⨯⨯=⋅-⋅⑥ 标量函数的梯度xy z u u u ux y ze e e ∂∂∂∇=++∂∂∂⑦ 求矢量的散度=y x z A xyzA A A ∂∂∂∇⋅++∂∂∂散度定理：矢量场的散度在体积V 上的体积分等于在矢量场在限定该体积的闭合曲面S 上的面积分，即VSFdV F d S ∇⋅=⋅⎰⎰，散度定理是矢量场中的体积分与闭合曲面积分之间的一个变换关系。

⑧ 给定一矢量函数和两个点，求沿某一曲线积分E dl ⋅⎰，x y CCE dl E dx E dy ⋅=+⎰⎰积分与路径无关就是保守场。

⑨ 如何判断一个矢量是否可以由一个标量函数的梯度表示或者由一个矢量函数的旋度表示？如果0A ∇⋅= 0A ∇⨯=，则既可以由一个标量函数的梯度表示，也可以由一个矢量函数的旋度表示；如果0A ∇⋅≠，则该矢量可以由一个标量函数的梯度表示；如果0A ∇⨯≠，则该矢量可以由一个矢量函数的旋度表示。

矢量的源分布为A ∇⋅ A ∇⨯.⑩ 证明()0u ∇⨯∇=和()0A ∇⋅∇⨯=证明：解 （1）对于任意闭合曲线C 为边界的任意曲面S ，由斯托克斯定理有()d d dSCCuu u l l ∂∇⨯∇=∇==∂⎰⎰⎰S l 由于曲面S 是任意的，故有()0u ∇⨯∇=（2）对于任意闭合曲面S 为边界的体积τ，由散度定理有12()d ()d ()d ()d SS S ττ∇∇⨯=∇⨯=∇⨯+∇⨯⎰⎰⎰⎰A A S A S A S 其中1S 和2S 如题1.27图所示。

第1章 矢量分析1、学习了矢量的基本概念和矢量的代数运算；2、学习了场的基本概念，场量的梯度、散度、旋度以及拉普拉斯运算；3、了解矢量分析过程中所需的恒等式和基本定理。

●矢量：既有大小又有方向的量，模为1的矢量即为单位矢量。

, A A A e A e A A==●矢量加法满足交换律和结合律，矢量减法不满足交换律。

()()(), , A B B A A B C A B C A B A B B A +=+++=++-=+-≠-●矢量的乘法两种：点积和叉积 ()()c o s ,(),+()==s i n ,,+()=x x y y z z n xy zx y zx A B A B A B B A A B C A B A C A B A B A B A B A B e A B A B B A A B C A B A C e e e A B A A A B θθ⋅=⋅=⋅⋅=⋅+⋅⋅++⨯⨯=-⨯⨯=⨯+⨯⨯交换律结合律直角坐标系中，分配律直角坐标系中，y zB B●场的基本概念：若空间中的每一个点都对应着某个物理量的一个确定值，就称在该空间中定义了这个物理量的场。

若这个物理量是标量，则这个场或函数称为标量场；若这个物理量是矢量，则这个场或函数称为矢量场。

标量场的梯度：max l x y z u grad u e u e e e l x y z∂∂∂∂==∇=++∂∂∂∂梯度的物理意义：标量场的梯度是一个矢量，大小等于标量函数在该点的最大的方向导数值，方向指向使函数值增加最快的方向。

矢量场的散度：0limy Sx z V F d S F F F div F F Vx y z∆→⋅∂∂∂==∇⋅=++∆∂∂∂⎰其中，=sF d S ψ⋅⎰是矢量F 穿过闭合曲面S 的通量。

旋度的物理意义：矢量场的散度是一个标量，表示在某处的单位体积内散发出来的矢量F 的通量，描述了通量源的密度。

矢量场的旋度：0max1limxy z CS xyze e e rot F n F dlF Sx y z F F F ∆→∂∂∂=⋅=∇⨯=∆∂∂∂⎰旋度 其中，CF dl ⋅⎰是矢量F 沿闭合路径C 的环流。

《电磁场与电磁波》复习指南第一章矢量分析考试范围：1—8节内容全部需要熟练掌握，其中，格林定理不做要求。

重点内容：矢量的定义、性质及表示方法；矢量的运算（点乘、叉乘、夹角）；三种常用的坐标系；面积元方向的定义；矢量场通量、环量的计算；标量场的梯度、矢量场的散度和旋度的定义、性质及计算公式；矢量恒等式（标量场梯度的旋度恒为零，矢量场旋度的散度恒为零）；拉普拉斯运算的定义、计算公式；散度定理、斯托克斯定理的含义及证明；亥姆霍兹定理的内容及意义（P29-30中的4小点说明）。

重点题目：习题 1.1 1.9 1.18 1.21 1.23例题P13 例1.3.1第二章电磁场的基本规律考试范围：1—7节内容全部需要熟练掌握。

重点内容：电荷密度、电流密度的定义、性质及计算公式；媒质极化和磁化的物理过程；极化强度、磁化强度的定义、计算公式及其与电场（或磁场）的关系；位移电流密度J 的定义和计算公式；麦克斯韦方程组的积分、微分形式，以及每个方程的名称及物理意义；媒质的本构关系；E、D、H、B各自的名称及相互区别；电磁场边界条件（P79 表2.7.1以及上面一段话）；入射角与折射角的数学关系；分界面两侧媒质的编号。

重点题目：习题 2.11 2.26 2.27 2.30 2.31例题P40 例2.2.1 P82例2.7.3第三章静电场及其边值问题的解考试范围：1—7节内容中，除以下章节外（3.1.5 静电力、3.3.5 磁场力、3.5.3导体柱面的镜像、3.5.4介质平面的镜像、3.6节分离变量法、3.7 节有限差分法、P97 部分电容，不做要求），其余内容需要熟练掌握。

重点内容：静电场的定义、性质以及所满足的基本方程；静电场中物理量（如电场强度、电位）的定义及性质；静电场的图形（矢量线）表示方法；静电场的计算；导体在静电场中的静电平衡以及静电平衡的特点；静电场中电通量的计算和性质；简单电容的计算；复杂电容的计算（串联、并联）；平板电容器电容的计算公式；导电媒质中恒定电流场的定义、性质和计算公式；欧姆定律的微分形式；漏电阻（漏电导）的计算；静电场与恒定电场的比拟；利用静电比拟法计算电容或电导（电容和电导是一对对偶量）；恒定电流场中的边界条件；矢量磁位A的定义及其与电流I的关系；静电场、恒定电场、恒定磁场的边界条件；静态场边值问题的分类及解法（解析法、数值法）；解析法包括镜像法和分离变量法；镜像法的基本思想和理论依据（实质），唯一性定理的内容和意义；电偶极子周围的电场分布和电位分布（电力线和等位线形状）。