材料力学1轴向拉压分析
- 格式:doc
- 大小:2.65 MB
- 文档页数:25

实验一材料在轴向拉伸、压缩时的力学性能一、实验目的1.测定低碳钢在拉伸时的屈服极限σs、强度极限σb、延伸率δ和断面收缩率 。
2.测定铸铁在拉伸以及压缩时的强度极限σb。
3.观察拉压过程中的各种现象,并绘制拉伸图。
4.比较低碳钢(塑性材料)与铸铁(脆性材料)机械性质的特点。
二、设备及仪器1.电子万能材料试验机。
2.游标卡尺。
图1-1 CTM-5000电子万能材料试验机电子万能材料试验机是一种把电子技术和机械传动很好结合的新型加力设备。
它具有准确的加载速度和测力范围,能实现恒载荷、恒应变和恒位移自动控制。
由计算机控制,使得试验机的操作自动化、试验程序化,试验结果和试验曲线由计算机屏幕直接显示。
图示国产CTM -5000系列的试验机为门式框架结构,拉伸试验和压缩试验在两个空间进行。
图1-2 试验机的机械原理图试验机主要由机械加载(主机)、基于DSP的数字闭环控制与测量系统和微机操作系统等部分组成。
(1)机械加载部分试验机机械加载部分的工作原理如图1-2所示。
由试验机底座(底座中装有直流伺服电动机和齿轮箱)、滚珠丝杠、移动横梁和上横梁组成。
上横梁、丝杠、底座组成一框架,移动横梁用螺母和丝杠连接。
当电机转动时经齿轮箱的传递使两丝杠同步旋转,移动横梁便可水平向上或相下移动。
移动横梁向下移动时,在它的上部空间由上夹头和下夹头夹持试样进行拉伸试验;在它的下部空间可进行压缩试验。
(2)基于DSP的数字闭环控制与测量系统是由DSP平台;基于神经元自适应PID算法的全数字、三闭环(力、变形、位移)控制系统;8路高精准24Bit 数据采集系统;USB1.1通讯;专用的多版本应用软件系统等。
(3) 微机操作系统试验机由微机控制全试验过程,采用POWERTEST 软件实时动态显示负荷值、位移值、变形值、试验速度和试验曲线;进行数据处理分析,试验结果可自动保存;试验结束后可重新调出试验曲线,进行曲线比较和放大。
可即时打印出完整的试验报告和试验曲线。

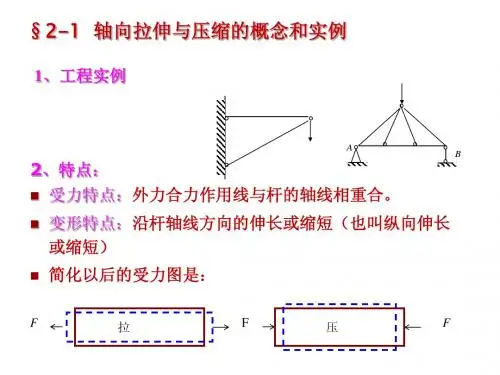



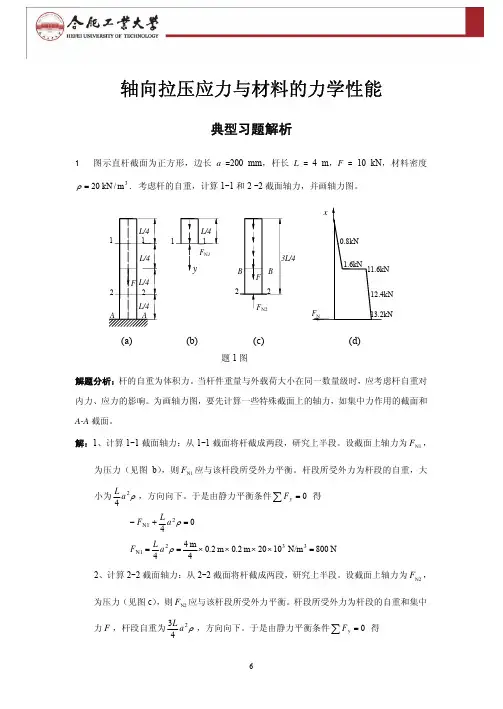
轴向拉压应力与材料的力学性能典型习题解析1 图示直杆截面为正方形,边长a =200 mm ,杆长L = 4 m ,F = 10 kN ,材料密度3m /kN 20=ρ. 考虑杆的自重,计算1-1和2 -2截面轴力,并画轴力图。
解题分析:杆的自重为体积力。
当杆件重量与外载荷大小在同一数量级时,应考虑杆自重对内力、应力的影响。
为画轴力图,要先计算一些特殊截面上的轴力,如集中力作用的截面和A-A 截面。
解:1、计算1-1截面轴力:从1-1截面将杆截成两段,研究上半段。
设截面上轴力为1N F ,为压力(见图b ),则1N F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重,大小为ρ24a L ,方向向下。
于是由静力平衡条件∑=0y F 得 042N1=+−ρa L F N 800N/m 1020m 2.0m 2.04m 44332N1=××××==ρa L F 2、计算2-2截面轴力:从2-2截面将杆截成两段,研究上半段。
设截面上轴力为N2F ,为压力(见图c ),则N2F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重和集中力F ,杆段自重为ρ243a L ,方向向下。
于是由静力平衡条件∑=0y F 得(c)(a) (b)题1图(d)kN 12.4N 104.12N/m 1020m 2.0m 2.04m43N 10104333332N2=×=×××××+×=+=ρa L F F 3、计算集中力F 作用截面上的轴力:首先将杆沿力F 作用截面(B-B )上侧截开,设截面上轴力为压力+B F N ,研究上半部分杆段。
由于只受本身重量作用,所以由静力平衡条件得F 作用截面上侧轴力为kN 1.6N 106.1N/m 1020)m 2.0(2m 4233322N =×=×××==+ρa L F B 然后将杆沿F 作用截面(B-B )下侧截开,设截面上轴力为压力−B F N ,研究上半部分杆段。

金属材料的拉伸、压缩实验承受轴向拉伸和压缩是工程构件最常见的受力方式之一,材料在拉伸和压缩时的力学性能也是材料最重要的力学性能之一。
常温、静载下金属材料的单向拉伸和压缩实验也是测定材料力学性能的最基本、应用最广泛、方法最成熟的试验方法。
通过拉伸实验所测定的材料的弹性指标E、μ,强度指标σs、σb,塑性指标δ、ψ,是工程中评价材质和进行强度、刚度计算的重要依据。
下面以典型的塑性材料——低碳钢和典型的脆性材料——铸铁为例介绍实验的详细过程和数据处理方法。
一、预习要求1、电子万能材料试验机在实验前需进行哪些调整?如何操作?2、简述测定低碳钢弹性模量E的方法和步骤。
3、实验时如何观察低碳钢拉伸和压缩时的屈服极限?二、材料拉伸时的力学性能测定拉伸时的力学性能实验所用材料包括塑性材料低碳钢和脆性材料铸铁。
(一)实验目的1、在弹性范围内验证虎克定律,测定低碳钢的弹性模量E。
2、测定低碳钢的屈服极限σs、强度极限σb、延伸率δ和断面收缩率ψ;测定铸铁拉伸时的强度极限σb。
3、观察低碳钢和铸铁拉伸时的变形规律和破坏现象。
4、了解万能材料试验机的结构工作原理和操作。
(二)设备及试样1、电子万能材料试验机。
2、杠杆式引伸仪或电子引伸仪。
3、游标卡尺。
4、拉伸试样。
GB6397—86规定,标准拉伸试样如图1所示。
截面有圆形(图1a)和矩形(图1b)两种,标距l0与原始横截面积A0比值为11.3的试样称为长试样,标距l0与原始横截面积A0比值为5.56的试样称为短试样。
对于直径为d0的长试样,l0=10d0;对于直径为d0的短试样,l0=5d0。
实验前要用划线机在试样上画出标距线。
(三)低碳钢拉伸实验1、实验原理与方法常温下的拉伸实验是测定材料力学性能的基本实验,可用以测定弹性模量E、屈服极限σs、强度极限σb、延伸率δ和断面收缩率ψ等力学性能指标。
这些指标都是工程设计中常用的力学性能参数。
现以液压式万能材料试验机为例说明其测量原理和方法。


1.衡。
设杆(A) qρ=(B)(C)(D)2.(A)(C)3. 在A和BA和点B(A) 0;(C) 45;。
4. 可在横梁(刚性杆)为A(A) [] 2A σ(C) []Aσ;5.(A)(C)6. 三杆结构如图所示。
今欲使杆3哪一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) (D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的?(A) pD ; (B) 2pD;(C) 4pD ; (D) 8pD 。
11.的铅垂位移12. 截面的形状为13. 一长为l挂时由自重引起的最大应力14. 图示杆112A A >是N1F F 题1-141. D 2. D 3. C 4. B 5. B 6. B 7. C 8. C 9. B 10. B11. Fl EA ;12. ab;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()s d πππd d ddddεε+∆-∆=== 证毕。
16. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11E A 和22E A 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
(假设圆杆和圆管之间不发生相对滑动)解: 由平衡条件 N1N2F F F += (1)变形协调条件N1N21122F l F lE A E A = (2) 由(1)、(2)得 N1111122F l F ll E A E A E A ∆==+E,17. 设有一实心钢杆,在其外表面紧套一铜管。
材料的弹性模量和线膨胀系数分别为1E2 Array证由18.解19.解20. 图示为胶合而成的等截面轴向拉杆,杆的强度由胶缝控制,已知胶的许用切应力[]τ为许用正力[]σ的1/2。
问α为何值时,胶缝处的切应力和正应力同时达到各自的许用应力。
解:2cos ασσα=≤[]σsin cos ατσαα=≤[]τ[]1tan []2τασ== 胶缝截面与横截面的夹角 57.26=α21.各杆直径为150 mm d =,许用应力[]σ=门受的水压力与水深成正比,水的质ρ=331.010 kg m ⨯,杆间的最大距离。
(取210 m s g =)解:设支杆间的最大距离为x ,闸门底部A集度为0q 。
闸门AB 的受力如图0A M ∑=,01314cos 2q F α⨯⨯=N F F =≤21[]π4d σ3cos 5α=,0330 kN m q gx x ρ== 得:9.42 m x = 22. 图示结构中AC 为刚性梁,BD 为斜撑杆,载荷F 可沿梁AC 水平移动。
试问:为使斜杆的重量最小,斜撑杆与梁之间的夹角θ应取何值? 解:载荷F 移至C 处时,杆BD 的受力最大,如图。
θcos h FlF BD =A ≥[]cos []BD F Flh σθσ=杆BD 的体积 2sin []sin 2h FlV Aθσθ== 当sin21θ=时,V 最小即重量最轻,故π454θ==423. 图示结构,BC 为刚性梁,杆1和杆2的横截面面积均为A ,和2[]σ,且12[]2[]σσ=。
载荷F 可沿梁BC (1) 从强度方面考虑,当x 为何值时,许用载荷[]F (2) 该结构的许用载荷[]F 多大? 解:(1) 杆BC 受力如图N1F =1[]A σ,N2F =2[]A σmaxN1N22133[][]2F F F A Aσσ=+==3lx =(2) F 在C 处时最不利 N2F F =≤2[]A σ 所以结构的许用载荷 2[][]F A σ=24. 图示结构,杆1和杆模量为E 且[]2[]σσ-+=,载荷F 虑杆的失稳,试求: (1) 结构的许用载荷[]F 。
(2) 当x 为何值时(0x <<解:(1) F 在B N12F F =(压) , N2F F =(拉)结构的许用载荷 [][]F A σ+=(2) F 在CD 正中间时能取得许用载荷最大值,此时N1N22FF F ==(压)-+N2B N2(1)12cot cos sin cos [][]l Fl l F V A A l αααασσ=+=+0d 0d Vααα==,()2200222000sin cos 10sin cos sin ααααα--=, 即22002200sin 2cos 0sin cos αααα-=0tan α=当054.74α=时,V 最小,结构用料最省。
26. 如图所示,外径为D ,壁厚为δ,长为l 的均质圆管,由弹性模量E ,泊松比ν的材料制成。
若在管端的环形横截面上有集度为q 的均布力作用,试求受力前后圆管的长度,厚度和外径的改变量。
解:长度的改变量 l lql l E Eσε∆=== 厚度的改变量 qEδνδεδνεδ'∆==-=-外径的改变量 D qD D D Eνενε'∆==-=-27.正方形截面拉杆,边长为,弹性模量200 GPa E =,泊松比0.3ν=。
当杆受到轴向拉力作用后,横截面对角线缩短了0.012 mm ,试求该杆的轴向拉力F 的大小。
解:对角线上的线应变0.0120.000340ε-'==- 则杆的纵向线应变0.001εεν'=-=杆的拉力160 kN F EA ε==28. 图示圆锥形杆的长度为l ,材料的弹性模量为E ,质量密度为ρ,试求自重引起的杆的伸长量。
解:x 处的轴向内力 ()()()N 13F x gV x g A x x ρρ==⋅杆的伸长量N00()d ()d ()3()l l F x x gA x x l x EA x EA x ρ⋅∆==⎰⎰20d 36l gx x gl E Eρρ==⎰29. 设图示直杆材料为低碳钢,弹性模量200 GPa E =,杆的横截面面积为25 cm A =,杆长 1 m l =,加轴向拉力150 kN F =,测得伸长 4 mm l ∆=。
试求卸载后杆的残余变形。
解:卸载后随之消失的弹性变形e 1.5 mm Fll EA∆== 残余变形为p e 2.5 mm l l l ∆=∆-∆=30. 图示等直杆,已知载荷F ,BC 段长l ,横截面面积A ,弹性模量E ,质量密度ρ,考虑自重影响。
试求截面B 的位移。
解:由整体平衡得43C F gAl ρ=BC 段轴力()N 43F x gA x l ρ⎛⎫=- ⎪⎝⎭截面B 的位移 ()N 020d 453d ()6lB BC l F x xΔl EA gA x l gl x EA Eρρ=∆=⎛⎫- ⎪⎝⎭==-↓⎰⎰ 31. 已知图示结构中三杆的拉压刚度均为EA ,设杆AB 为刚体,载荷F ,杆AB 长l 。
试求点C 的铅垂位移和水平位移。
解:杆AB 受力如图N20F =, N1N32FF F ==132y FlΔl l EA=∆=∆=因为杆AB 作刚性平移,各点位移相同,且N20F =,杆2不变形。
又沿45由A 移至A '。
所以 2x y FlΔΔEA==32. 电子秤的传感器是一个空心圆筒,承受轴向拉伸或压缩。
已知圆筒外径80 mm D =,壁厚9 mm δ=,材料的弹性模量210 GPa E =。
在称某重物时,测得筒壁的轴向应变647610ε-=-⨯,试问该物重多少?l=1kNN3'xΔ解:圆筒横截面上的正应力FE Aσε== ()221π4F EA E D d εε==⋅-262 mm d D δ=-= 该物重 200.67 kN F =33. 图示受力结构,AB 为刚性杆,CD 为钢制斜拉杆。
已知杆CD 的横截面面积2100 mm A =,弹性模量200 GPa E =。
载荷1 5 kN F =,210 kN F =,试求: (1) 杆CD 的伸长量l ∆; (2) 点B 的垂直位移B ∆。
解:杆AB 受力如图0A M =∑,N2120F F F --=)N 212F F F =+=N 2 mm F ll EA∆==2 5.66 mm B C ΔΔl ===34. 如图示,直径16 mm d =的钢制圆杆ABB 处铰接。
当D 处受水平力F 0.0009ε=。
已知钢材拉伸时的弹性模量E =(1) 力F 的大小; (2) 点D 的水平位移。
解:折杆BCD 受力如图(1)0C M ∑=,N 1.520F F ⨯-⨯=N1.5 1.528.5kN 22F F E A ε=== (2)0.0018 m 1.8 mm l l ε∆=== 2 1.5Dx Δl∆=2 2.4 mm 1.5Dx Δl ε==11B35. 如图示等直杆AB 在水平面内绕A 端作匀速转动,角速度为ω,设杆件的横截面面积为A ,质量密度为ρ。
则截面C 处的轴力N C F = 。
答:22x A x l ρω⎛⎫- ⎪⎝⎭36. 如图示,两端固定的等直杆AB ,已知沿轴向均匀分布的载荷集度为q ,杆长为l ,拉压刚度为EA ,试证明任意一截面的位移()2x qx l x EA δ-=,最大的位移2max 8ql EA δ=。
证:由平衡条件得0A B F F ql +-=()2 N 0 0d d 2ll AA F qx x F x F l ql l EA EA EA EA-∆===-⎰⎰ 由变形协调条件0l ∆=,得2A qlF =22d 222xA A x F qx F x qx ql x qx x EA EA EA EA EA δ-==-=-=⎰令0x δ'=,20ql qx -= 即当2lx =时,杆的位移最大,2max 2228l l q l qlEA EAδ⎛⎫- ⎪⎝⎭==证毕。
37. 图示刚性梁AB ,在BD 两点用钢丝悬挂,钢丝绕进定滑轮G 、F ,已知钢丝的弹性模量210 GPa E =,横截面面积2100 mm A =,在C处受到载荷20 kN F =的作用,不计钢丝和滑轮的摩擦,求C 点的铅垂位移。
解:设钢丝轴力为N F ,杆AB 受力如图示。