当前位置：文档之家 › 第三章货币的时间价值

第三章货币的时间价值

  • 格式：ppt
  • 大小：1.91 MB
  • 文档页数：68

下载文档原格式

  / 68

合集下载

第三章现值与现值技术

第三章现值与现值技术

方法。 所谓单利是只计算本金所带来的利息，而不考虑利
息再产生的利息。 单利终值是指一定时期以后的本利和。它是若干期
以后包括本金和利息在内的未来价值。
例
现在的1元钱，年利率为10%，从第1年到第 3年各年年末的终值可计算为：
1元1年后的终值=1×（1+1×10%）=1.1(元) 1元2年后的终值=1×（1+2×10%）=1.2(元) 1元3年后的终值=1×（1+3×10%）=1.3(元)
或=A×[(P/A,10%,10-1)+1]
=120×(5.759+1)=811.08（元）
计算结果表明租比购买好。
3、延期年金
延期年金是指在最初若干期没有收付款项的 情况下，后面若干期等额的系列收付款项。 假设最初有m期没有收付款项，后面n期有等 额的收付款项。
递延年金的终值大小与递延基数无关，所以 计算方法与后付年金终值计算方法相同。
预付年金终值=A×（F/A，10%，10）× （1+10%）
=1000×15.937×(1+10%)=17530.7(元)
或=A×[(F/A,10%,11)-1]=1000×(18.5311)=17531(元)
（2）预付年金现值
收入或支付在每期期初的系列等额收、付款 的现值之和，称为预付年金现值。
PAA i
1
式中:Leabharlann 1in称年金复利现值，系 用P数/ A，，,n表示，可查表。得
i
例
华夏公司准备购买一台设备，有两个方案可供选择， 一是向甲厂购买，分三年付款，每年年末支付10万 元；二是向乙厂购买，需当即一次性支付25万元。 银行利率10%，问采用哪个方案更经济？
货币时间价值、

货币时间价值、

第三章货币时间价值讲授内容：第一节货币时间价值一、基本概念及符号（一）时间轴顾名思义，时间轴就是能够表示各个时间点的数轴。

如果不同时间点上发生的现金流量不能够直接进行比较，那么在比较现金数量的时候，就必须同时强调现金发生的时点。

如图3-1所示，时间轴上的各个数字代表的就是各个不同的时点，一般用字母t表示。

（二）单利和复利单利和复利是两种不同的利息计算体系。

在单利（simple interest）情况下，只有本金计算利息，利息不计算利息；在复利（compound interest）情况下，除本金计算利息之外，每经过一个计息期所得到的利息也要计算利息，逐期滚算，俗称“利滚利”。

（三）现值和终值现值即现在（t=0）的价值，是一个或多个发生在未来的现金流相当于现在时刻的价值，用PV（Present value的简写）表示。

终值即未来值（如t=n时的价值），是一个或多个现在发生或未来发生的现金流相当于未来时刻的价值，用FV（Future value的简写）表示。

（四）单一支付款项和系列支付款项单一支付款项是指在某一特定时间内只发生一次的简单现金流量，如投资于到期一次偿还本息的公司债券就是单一支付款项的问题。

系列支付款项是指在n期内多次发生现金流入或现金流出。

年金是系列支付款项的特殊形式，是在一定时期内每隔相同时间（如一年）发生相同金额的现金流量。

年金（用A表示，即Annuity的简写）可以分为普通年金、预付年金、递延年金和永续年金等形式。

1.普通年金普通年金又称为后付年金，是指一定时期内，每期期末发生的等额现金流量。

例如从投资的每年支付一次利息、到期一次还本的公司债券中每年得到的利息就是普通年金的形式。

普通年金，既可以求现值，也可以求终值。

2.预付年金预付年金又称为先付年金，是指一定时期内，每期期初发生的等额现金流量。

例如对租入的设备，如果要求每年年初支付相等的租金额，那么该租金就属于预付年金的形式。

与普通年金相同，预付年金也既可以求现值，也可以求终值。

自考金融学第三章

自考金融学第三章


A.单利率和复利率
B.固定利率和浮动利率 C.名义利率和实际利率 D.基准利率、一般利率和优惠利率 【答案】 C
【例3-18 单选】由金融市场的资金供求状况决定的利率是( A.基准利率 B.市场利率 C.官定利率
)。
D.名义利率
【答案】 B
【例3-19 单选】由非官方机构的行业自律组织加以规定的，对组 织成员有一定的约束力，这种利率是( )。
)。
某存款账户上有1000元，年利率为10％，期限为n年。单利计息
第一年末，本利和应该是：
S1 1000 1000 10% 1000 1 10% 1100
第二年末，本利和应该是：
S 2 1000 1000 10% 2 1000 1 10% 2 1200
（四）实际利率与名义利率
（五）年利率、月利率和日利率
（一）基准利率
1.定义 （1）基准利率指多种利率并存条件下起决定作用的利率。
（2）基准利率指在整个金融市场上和整个利率体系中处于关键地位、起决定
性作用的利率。 （3）决定作用：基准利率发生变动，其他利率也会随之发生相应的变动。
2.分类：
（1）市场基准利率：通过市场机制形成的无风险利率，一般把安全性高、风 险性低的货币市场利率作为无风险利率的代表。如国债利率、同业拆借利率等。
)。
（二）现值与终值
1.终值：未来某一时点的本利和。 单利的终值：S=P（1+r×n）
复利的终值：S=P（1+ r）n
2.现值：未来某一时点上一定的货币金额的现在价值。 单利的现值：P=S÷（1+r×n） 复利的现值：P=S÷（1+ r）n
【例3-11 单选】(
)是指一笔货币资金按照一定的利息率水平
3(第三章)利息和利率

3(第三章)利息和利率

利息与利率导读：当利率上升时，债券价格会下降，股票市场也会下跌，为什么会如此？通过本章的学习，你会得到这些问题的答案。

第一节利息与收益的一般形态（一）货币时间价值与利息1.货币时间价值：指同等金额的货币其现在的价值要大于其未来的价值。

（货币为什么具有时间价值？理论界解释：就现在消费与未来消费来说，人们更加偏好现在消费，如果货币的所有者要将其持有的货币进行投资或借予他人进行投资，他就必须牺牲现在消费，对此，他会要求对其现在消费的推迟给予一定的补偿，补偿金额的多少与现在消费推迟的时间成同向变动。

因此，货币时间价值来源于对现在消费推迟的时间补偿。

）马克思对利息来源的经典阐述：“贷出者和借入者都是把同一货币额作为资本支出的。

但它只有在后者手中才执行资本职能。

同一货币额作为资本对于两个人来说取得了双重的存在，这并不会使利润增加一倍。

他所以能对双方都作为资本执行职能，只是由于利润的分割。

其中贷出者的部分叫利息。

由此可见，利息来源于再生产过程是生产者借入资金发挥营运职能而形成的利润的一部分。

2.利息与收益的一般形态（1）利息转化为收益的一般形态利息通常被人们看作是收益的一般形态——利息是货币资金所有者理所当然的收入。

（2）收益的资本化将任何有收益的事物通过收益与利率的对比倒算出该事物相当于多大的资本金额，这便是收益的资本化。

C = P * r C(收益) 本金（P）利率（r）收益的资本化公式：P = C / r收益资本化作用的领域非常广泛，土地交易、证券买卖、人力资本的衡量等。

地价= 土地年收益/ 年利率人力资本价格= 年薪/ 年利率股票价格= 股票收益/ 市场利率第二节利率的计量和种类（一）计量1.单利与复利单利公式：C(利息) = P（本金）* r（利率）* n（年限）复利公式：S(本利和)=P（本金）*{（1+r）的n次方}C = P 【（1+r）的n次方– 1】2.现值与终值终值：按一定的利率水平计算出来其在未来某一点上的金额（即本利和）现值：与终值相对应，这笔货币资金德本金额被称为现值（即未来本利和的现在价值）公式：P = S / (1+r)的n次方3.到期收益率到期收益率：指投资人按照当前市场价格购买债券并且一直持有到债券期满时可以获得的年平均收益率。

《财务管理基础》第13版课后答案3-16章全解

《财务管理基础》第13版课后答案3-16章全解

《财务管理基础》第13版课后答案3-16章全解第三章货币的时间价值4．你在第⼗年年末需要50000美元。

为此，你决定在以后10年内，每年年末向银⾏存⼊⼀定的货币额。

若银⾏长期存款的年利率为8%，则你每年要存⼊多少钱才能在第⼗年年末获得50000美元。

（近似到整数）？【答】求贴现率8%，终值为50000美元的年⾦⾦额。

查表A3，（F/A，8%，10）＝14.487。

所以，A=F/（F/A，8%，10）＝50000/14.487＝3451.37美元。

【答】求解现值，贴现率14%。

分开不同⾦额计算：1. P6-10＝A×（P/A，14％，5）×（P/F，14％，5）＝1400×3.433×0.519=2494.42；P5＝1600×（P/F，14％，5）=1600×0.519＝830.4；P4＝1900×0.592=1124.8；P3＝2400×0.675=1620；P2＝2000×0.769=1538；P1＝1200×0.877=1052.4；P1-10＝2494.42＋830.4＋1124.8＋1620＋1538＋1052.4＝8660.02美元。

10.假设你将在第⼗年年末收到1000美元.如果你的机会成本利率(opportunity rate)是10%,那么在计息期分别是(1)每年计息⼀次, (2)每季计息⼀次,(3)永续计息时的现值各是多少?【答】（1）每年计息⼀次，P=F*(P/F，10％，10)=0.386*1000=386美元。

（2）每季度计息⼀次，P=F*(P/F，10％/4，10*4)；美元查表A2 表不能直接查到，3%的现值=0.453*1000=453美元，2%的现值=0.307*1000=307美元，⽤插值法可得P＝380美元。

（3）永续计息P=1000/2.718280(0.1*10）=367美元。

工程经济学 第三章 资金的时间价值

工程经济学 第三章 资金的时间价值

F=P(1+i)n
.
复利法的计算
年份
年初本金P
1
P
2 P(1+i)
当年利息I
P·i P(1+i) ·i
年末本利和F
P(1+i) P(1+i)2
… … … …
n－1 P(1+i)n-2 P(1+i)n-2 ·i P(1+i)n-1 n P(1+i)n-1 P(1+i)n-1 ·i P(1+i)n
n年末本利和的复利计算公式为: F= P(1. +i)n
资金的时间价值一般用利息和利率来度量。 1、利息
就是资金的时间价值。它是在一定时期内， 资金的所有者放弃资金的使用权而得到的补偿 或借贷者为获得资金的使用权所付出的代价。 通常情况下，利息的多少用利率来表示。在工 程经济学中，“利息”广义的含义是指投资所 得的利息、利润等，即投资收益。利息通常用 “I”表示。
资金产生价值的条件： 第一，投入生产或流通领域； 第二，存在借贷关系。
资金的时间价值是客观存在的，只要商品生产存在， 资金就具有时间价值。
通货膨胀是指由于货币发行量超过商品流通实际需要 量而引起的货币贬值和物价上涨现象。
.
资金的价值不只体现在数量上，而且表现在时间上。 投入一样，总收益也相同，但收益的时间不同。
I代表总利息
P代表本金
i代表利率
n代表计息周 期数
单利虽然考虑了资金的时间价值，但对以前 已经产生的利息并没有转入计息基数而累计 计息。因此，单利计算资金的时间价值是不 完善的。
.
（二）复利
将本期利息转为下期的本金，下期按本期 期末的本利和计息，这种计息方式称为复利。 在以复利计息的情况下，除本金计算之外，利 息再计利息，即“利滚利”。
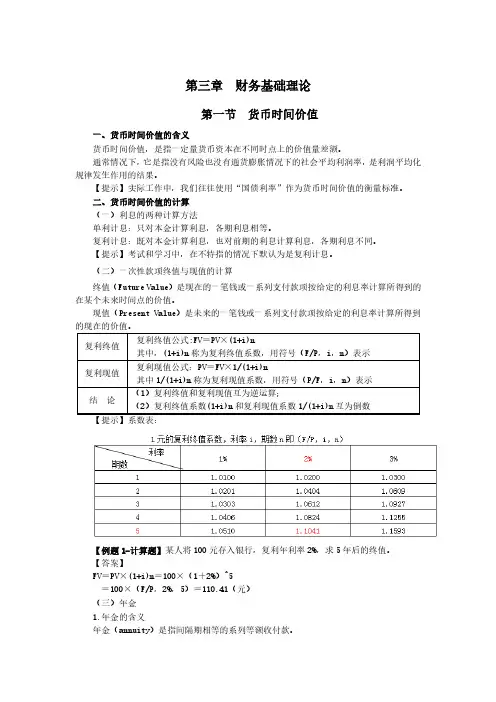
财务管理核心考点精讲 第三章 财务基础理论

财务管理核心考点精讲 第三章 财务基础理论

【答案】
甲公司付款终值＝10×（F/A，15%，10）＝203.04（亿美元） 乙公司付款终值＝40×（F/P，15%，10）＋60×（F/P，15%，2）
＝241.174（亿美元） 甲公司付款终值小于乙公司，因此，A 公司应接受乙公司的投标。 【提示】实际工作中，对上述问题的决策多采用比较现值的方式进行。
6.2469
【例题 2-计算题】小王是位热心于公益事业的人，自 2005 年 12 月底开始，他每年年
末都要向一位失学儿童捐款。小王向这位失学儿童每年捐款 1 000 元，帮助这位失学儿童从
小学一年级读完九年义务教育。假设每年定期存款利率都是 2%，则小王 9 年的捐款在 2013 年年底相当于多少钱？
（五）其他年金
1.预付年金
（1）预付年金终值的计算
方法 1：利用同期普通年金的公式乘以（1+i） 方法 2：利用期数、系数调整 FV＝A（F/A，i，n＋1）－A
＝A[（F/A，i，n＋1）－1]
【提示】预付年金终值系数与普通年金终值系数的关系：期数加 1，系数减 1。
【例题 6-计算题】为给儿子上大学准备资金，王先生连续 6 年于每年年初存入银行 3 000 元。若银行存款利率为 5%，则王先生在第 6 年年末能一次取出本利和多少钱？
②偿债基金系数和普通年金终值系数的互为倒数； ③年资本回收额与普通年金现值互为逆运算； ④资本回收系数与普通年金现值系数互为倒数。
【例题 5-单选题】在下列各项货币时间价值系数中，与资本回收系数互为倒数关系的 是（ ）。
A.（P/F，i，n） B.（P/A，i，n） C.（F/P，i，n） D.（F/A，i，n） 【答案】B 【解析】普通年金现值系数与资本回收系数互为倒数关系。
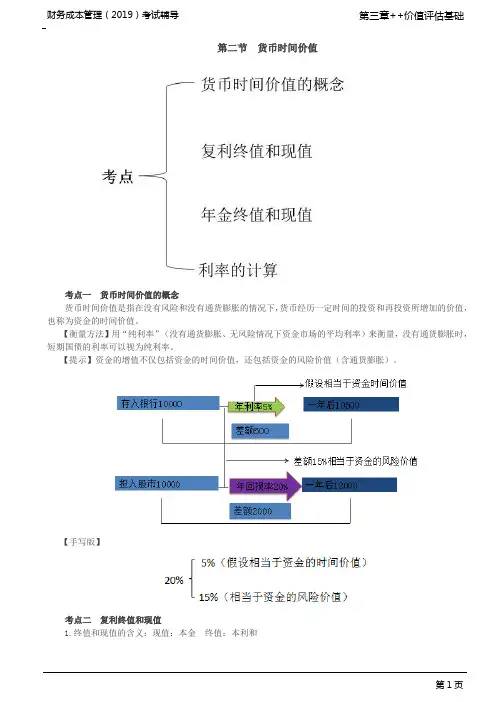
货币时间价值的概念、复利终值和现值、年金终值与现值(1)

货币时间价值的概念、复利终值和现值、年金终值与现值(1)

第二节货币时间价值考点一货币时间价值的概念货币时间价值是指在没有风险和没有通货膨胀的情况下，货币经历一定时间的投资和再投资所增加的价值，也称为资金的时间价值。

【衡量方法】用“纯利率”（没有通货膨胀、无风险情况下资金市场的平均利率）来衡量，没有通货膨胀时，短期国债的利率可以视为纯利率。

【提示】资金的增值不仅包括资金的时间价值，还包括资金的风险价值（含通货膨胀）。

【手写版】考点二复利终值和现值1.终值和现值的含义：现值：本金终值：本利和2.计算公式中使用的表达符号：P:现值F:终值i：计息期利率n:计息期数3.计算的基本方法（复利计息方法）：【解释】复利计息方法就是“利滚利”，（本金计息、前期的利息也计息）4.复利终值的计算（一次性收付款项的终值的计算）：F=P(1+i)n式中，(1+i)n为复利终值系数（教材附表1），记作（F/P，i，n）；n为计算利息的期数。

【例题·计算题】某人将100元存入银行，复利年利率为2%，求5年后的终值。

【分析】F=P（1+i）n=100×（F/P，2%，5）=100×1.1041=110.41（元）5.复利现值的计算（一次性收付款项的现值的计算）P=F(1+i)-n式中(1+i)-n为复利现值系数（教材附表2），记作（P/F，i，n）；n为计算利息的期数。

【例题·计算题】某人存入一笔钱，想5年后得到10万，若银行存款利率为5%，要求计算按照复利计息，现在应存入银行多少资金？【分析】按照复利计息：P＝10×（1+5%）-5=10×（P/F，5%，5）＝10×0.7835＝7.835（万元）。

【总结】（1）复利终值和复利现值互为逆运算。

（2）复利终值系数（1＋i）n和复利现值系数1/（1＋i）n互为倒数。

考点三年金终值与现值【年金的含义】：金额相等、间隔时间相同的系列收支。

【提示】年金用符号“A”表示。

第三章 资金的时间价值及其等值计算 《金融经济学》PPT课件

第三章 资金的时间价值及其等值计算 《金融经济学》PPT课件

在一般的场合，资金的使用具有机会成本与资金具有时间价 值是两个互为等价的说法。
资金时间价值的大小取决于多方面的因 素。主要有：
1.无风险投资收益率。 2.通货膨胀率，即为抵销货币贬值所应 考虑的部分。
3.风险贴水，即为补偿风险损失所应计 入的部分。又叫做风险报酬率。
计算单位资金时间价值的基本方法有两种：
1000（1+1%×12）—100
=1000（1+12%）—1000=12（元）
这时的年实际利率等于年名义利率。因此，只 有在复利的计算中才会出现名义利率和实际利率的 不同。所谓实际利率与名义利率的差异实质上是按 复利计算的利息水平与按单利计算的利息水平的差 异。
因此，我们可以将年名义利率定义为每一计息 周期的利率与每年的计息周期数的乘积。而年实际 利率则为运用普通复利计算方法得到的年利率。
0.04=(1+i)2 —1 解之得： i=0.0198
因此每季度存款100元，季度利率为1.98%，计息期数为 4×8=32时的期末终值为：
100（F/A，1.98%，32）
四、连续复利 上述分析表明，名义利率相同，计息周 期越短，实际年利率就越高。如果一年之中 计算利息m次，则n 年后之本利和为：
1000（1+1%）12—1000=127（元）。 年实际利率为127/1000=12.7%。与年实际利率12.7%相对 应，我们把年利率12%称为年名义利率。 显然，只有当实际计息周期与合同利率的时间单位不一 致时，才会出现名义利率与实际利率的差别。
如果银行改为每月按单利计息一次，则该人年 末可获利息：
令m=rk，代入上式，则有：
当一年之中计息次数无限增多，即m→∞ 时，则有K→∞，因此有：
由此，当m→∞时，名义利率r 与实际利 率 的关系式可以进一步简化：
第三章+++利息与利息率

第三章+++利息与利息率


市场利率：由货币资金的供求关系直接决定并由
借贷双方自由议定的利率，其市场规律
而自由变动。
官定利率：一国货币管理部门或中央银行所规定 的利率。 行业利率：由非政府部门的民间组织为了维护公平 竞争所确定的利率。
（三）按照借贷期内利率是否浮动可划分为：
固定利率：在整个借贷期内不随市场上货币资金 供求状况的变化而相应调整的利率。 浮动利率：在整个借贷期内根据市场上货币资金 供求状况的变化而定期调整的利率。
第三章
第一节
利息与利率
利息与收益的一般形态
一、货币的时间价值与利息 货币的时间价值：同等金额的货币其现在的
价值要大于其未来的价值。
马克思的利息来源的论述：
利息来源于利润的一部分。
二、利息与收益的一般形态 （一）利息转化为收益的一般形态
（二）收益的资本化
将有收益的事物通过收益与利率的对比倒
算出该事物相当于多大的资本金额。
中国的习惯：不管是年利率、月利率还是日利 率，均用“厘”作单位，但意义不同。 年息5厘指5%，月息5厘指0.5%， 日息（拆息）5厘指0.05%。
第三节
一、利率决定理论
利率的决定与影响因素
（一）马克思的利率决定理论
取决于平均利润率，介于0与平均利润率之间。
（二）西方利率决定理论
1、传统利率决定理论：取决于储蓄和投资 2、凯恩斯的利率决定理论：货币供求 3、可贷资金论：取决于可贷资金的供求
C、等于
B、低于
D、上述均有可能 ）
7、某公司的股票预计每年可派发股息2元/股，
利率为5%，则该公司的理论股价是（ A、2元 B、20元 C、40元 D、1元
8、凯恩斯的利率决定论认为利率取决于（ A、储蓄和投资 B、货币供求
技术经济与企业管理第三章资金的时间价值

技术经济与企业管理第三章资金的时间价值

答：购买者可获年利率为9.2% 。
技术经济与企业管理第三章资金的时 间价值
二、复利计算公式
• 复利公式计算符号如下： P：现值，i：
折现率，n：时间周期数，F：终值，A： 等额年金
技术经济与企业管理第三章资金的时 间价值
1.复利终值公式，
复利终值公式（已知现值P，求终值F），该问题可用如
下现金流图表示。
n
年
技术经济与企业管理第三章资金的时 间价值
4.偿债基金公式
偿债基金公式（已知终值F，求年金A），该问题可用如 下现金流图表示。
0 1 2 ···· A＝？
F
n 年
技术经济与企业管理第三章资金的时 间价值
5.年金现值公式
年金现值公式（已知年金A，求现值P），该问题可用如 下现金流图表示。
A
0 1 2 ····· P=?
期数（期末） 期初本金
本期利息
期末本利和
1
P
2
P
3
P
…
…
n
P
Pi
F1=P(1+i)
Pi
F2=P(1+2i)
Pi
F3=P(1+3i)
…
…
Pi
Fn=P(1+ni)
技术经济与企业管理第三章资金的时 间价值
2.复利法：复利计息时，不仅本金计息，而且利
息也生息。即把前期中的利息加到本金中去，作
为本金的计息本金。复利计息更符合资金在社会
在计息期的期末；
•
(3)本期的期末即为下期的期初；
•
(4)现值P是当前期间开始时发生的；
•
(5)将来值F是当前以后的第n期期末发生的；
•

第三章-2 (第8节+课后习题)资金的时间价值

例：假设我国银行存款利息为：一年1.98％；三年2.52％，
现有10000元存三年定期与一年定期存三年，哪种利息高？
10000× 252％×3＝756（元） 10000×1.98％＝198 10198×1.98％＝201.9 (10000+198+201.9)×1.98％＝205.9 198+201.9+205.9=605.8（元）
n F P( i) n1 P( i) n1 i P( i) n 1 1 1 n 商业贷款是复利计算的。 复利计算符合扩大再生产的理论和实践，所以常用复利。
例3 如前例，如果以复利来算，则2年后的利息和本利和为多少？ 解： I 1000[(1 10%)2 1] 210 （元）
把这种在一定的利率下，在不同时点上的绝 对数额不同，而价值相等的若干资金称为等值资
金。
影响资金等值的因素： n资金额的大小 n计息周期的多少 n利率的大小。
按照资金等值的概念，把一个时点上的资金换算成另
一个时点上的与之相等的资金值，这一换算过程即资金的 等值计算。
（二）
准备：基本参数

等值计算公式
0 P 1 2 3 n-1 n
计算公式： F= P（1＋ i ）n
F＝250 000×(1+5%）8
= 250 000 ×1.477 = 369 250（元）
2.一次支付现值公式(一次支付型)
P
或：
1 i
F

n
P F P / F i n
0 1 2 3 4
(1+i)-n称一次支 付现值系数可记为 (P/F，i，n) 1 P / F i n n 1 i

财务管理第三章时间价值与风险价值


n期预付年金 n期普通年金
PA=?
1
2
2
3
3
PA=?
0 1
1 − ( 1 + i) − n × ( 1 + i) P = A × i A 1 + i − ( 1 + i) − n + 1 = A × i 1 − ( 1 + i) − ( n − 1 ) + 1 ) = A × ( i
31
先付年金现值
23
普通年金终值计算 普通年金终值计算
一定时期内，每期期末等额系列 收付款项的复利终值之和。
(1 + i ) − 1 F = A× i
n
年金终值系数 (F/A,i,n)，如
何得来？ 何得来？
可通过查年金现值系数表求得 (P/A,i,n)
24
普通年金终值计算 普通年金终值计算
P43，例3-4 例3-5，已知终值求年金 偿债基金，是年金终值的逆运算；偿债 基金系数，是年金终值系数的倒数，记 作（A/F，i，n）
P47，例3-7，比较现值，选取较小的方 案 （1）先付年金现值 （2）递延年金，m=3？？？
×(P/F,i,m)
35
方法2 方法2：假定递延期m期有年金 递延年金的现值PA =A(P/A,i,m+n)-A(P/A,i,m)
36
n期 期
A(F/A,i,n)
方法3：先求出n点的年金终值，再求出0期现值 方法3 递延年金的现值PA
=A(F/A,i,n) ×(P/F,i,n+m)
37
递延年金终值与现值的应用
18
3、复利现值：是指未来一定时间的特定资金 按复利计算的现在价值. F = P（1 + i ）n （

第3章 含时间因素的货币等值计算

单利 24 (1 8% 374) 742 （美元）
复利 F 24 (1 8%)374 76 （万亿美元）
到2000年，这24美元复利计息将变成约76万亿美元，几乎是其2.5万 亿美元价值的30倍。而按照单利计算这24美元仅变成742美元。
工业工程教研室 赵晶英
10
3.2 利息公式
(二) 等值的含义
解 其现金流量如图3-10所示。 每年向银行借一次，支付期为1年，年利率为12%，每季度
计息一次，计息期为一个季度，属计息期短于支付期。由于利 息按季度计算，而支付在年底。这样，计息期末不一定有支付， 所以例题不能直接采用利息公式，需要进行修改，使之符合计 息公式，修改方法有如下三种：
A1 ：等额的年末支付 ，是已知的 ；
A2 ：通过等额支付系列积累基金公式求得
A2
G
1 i
n i
A/
F,i, n
或
A2 GA / G,i, n
附录A7 P262-263
工业工程教研室 赵晶英
18
3.2 利息公式
例3-2 假定某人第一年末把1000元存入银行，以后9
年每年递增存款200元。如年利率为8%，若这笔存款
F
01
2
3
n-1
n
A
A
A
AA
图3-5 一次支付复利现金流量图
附录A3 P254-255
F A 1 in 1
i
F=A（F/A，i，n）
工业工程教研室 赵晶英
14
3.2 利息公式
4.等额支付系列积累基金公式
A
F
1
i
in
1
i
1
in
1
叫作等额支付系列积累基金系数

PDE3




方法三 把等额支付的每一个支付看作为一次支付， 求出每个支付的现值。
P 500 P 3,4 500 P 3,8 500 P 3,12 F F F 500 P 3,16 500 P 3,20 500 P 3,24 F F F 2024(元)


i A F n (1 i) - 1 F ( A / F ,5%,3) 2 0 0 0.3 1 7 2 1 6 3.4 4 2
5.等额支付系列资金恢复公式
i(1 i) A P n (1 i) 1
n
式中i(1+i)n/[(1+i)n-1]为等额支付系列资金恢复系数， 记为（A/P, i,n)
解：
FP F

P
i ,10
2000 1000 F
F P i ,10 2


i ,10
P

查附表一，当n=10，2落于7%和8%之间 i=7%时 F P 7,10 1.9671
i=8%时 F P 8,10 2.1589 用直线内插法可得：
i 0.07 0.01
2.0000 1.9671 0.07 0.0017 7.17% 2.1589 1.9671
例2: 6年期付款购车，每年初付2万元，设年利 率为10%，相当于一次现金支付的购价为多少？
P A A( P / A, i, n) 2 2(P/A,10%,5 ) 2 2 3.791 9.582
计息期短于支付期
例1：年利率12%，每季度计息一次，每年年末 支付500元，连续支付6年，求其第0年的现值为 多少？ 解：其现金流量如图
计息期为季度，支付期为1年，计息期短于支付 期，该题不能直接套用利息公式。

《财务管理基础第13版》10-16章答案


【解答】预期收益率R=0.07+（0.12-0.07）*1.67=0.1538 6．目前，无风险收益率为10％，市场组合的期望收益率是15％，市场 分析专家对四种股票的收益率和贝塔的预期见下表：
股票
预期收益率
预期贝塔
1
Stillman锌矿公 17.0％
1.3
司
2
Union油漆公司 14.5
0.8
3
c. 零售联销会使股利增长率增至10%,要求的报酬率也上升到
14%.【解答】股价=1.5/（.14-.10）=37.5/股
从股票的每股市价判断,那一种策略最好? 【解答】a策略和c策略在
影响股价上的作业相同。
11. Great Northern Specific 铁路公司有一种不回收的永久债券发行在外.
发生的概 0.10
0.20
0.30
0.30
0.10
率
可能收益 －0.10 0.00
0.10
0.20
0.30
率
a. 投资的期望收益率和标准差是多少？【解答】期望收益率 =0.1*-0.1+0.2*0+0.3*.1+.2*.2+.3*.1=-0.01+0+0.03+0.06+0.03=0.11; 标准差=std( sq0.21*.1+sq0.11*.2+sq0.01*.3+sq0.09*.3+sq0.19*.1)=std(0.00441+0.00242+0.00
财务管理作业—刘潜—第3-9章
第三章 货币的时间价值 4．你在第十年年末需要50000美元。为此，你决定在以后10年内，每年 年末向银行存入一定的货币额。若银行长期存款的年利率为8%，则你 每年要存入多少钱才能在第十年年末获得50000美元。（近似到整 数）？ 【解答】求解年金金额，贴现率8%。终值为50000美元的年金金额。查 表A3,利率8%，1美元年金的10年终值比例为14.487。所以，每年需要储 蓄的金额是50000/14.487=3451.37美元/年。 9．H&L Bark 公司正考虑买入一台预计机器产生的现金流量如下：

财务管理 第三章





年利率则有名义利率和实际利率之分。 名义利率，是指每年结息次数超过一次时的年 利率。 实际利率，是指在一年内实际所得利息总额与 本金之比。


显然,当且仅当每年计息次数为一次时，名义利 率与实际利率相等

如果名义利率为r,每年计息次数为m,则每次计息 的周期利率为r/m

FVIF i，n

例2：某人将20,000元存放于银行，年存款利率 为6%，在复利计息方式下，三年后的本利和为 多少。

复利现值是指未来年份收到或支付的现金在当前的价值。
一元人民币的现值
时
间（年）
复利现值与利率及时间之间的关系

由终值求现值，称为贴现，贴现时使用的利息率称为贴现率。
FVn PV (1 i ) n FVn PV n (1 i )




如果我从第2年年末开始每年末存入银行1万元, 银行利率为5%,第五年年末我可以从银行取出多 少资金?

如果我从现在开始每年初存入银行1万元,银行利 率为5%,第三年年末我可以从银行取出多少资金?
2、预付年金/期初年金

预付年金/期初年金:每期期初有等额收付款项的年金 方法一： F= A (F/A , i , n+1) – A = A[(F/A , i , n+1) – 1] 方法二: F = A（F/A ，i ，n）(1+i ) =普通年金终值*(1+i )
第三章估价导论
第三章估价导论

第一节 货币的时间价值

第二节 贴现现金流量 第三节 时间价值计算中的几个特殊问题

第一节货币的时间价值
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、经营决策
（一）投资方案的可行性评估 o 从财务上看，净现值大于0的方案可行，几个方
案中净现值最大的方案最佳。 （二）投资借款偿还金额的确定 o 利用年金现值公式求解每年应偿还的借款数额。 （三）票据贴现
PPT文档演模板
第三章货币的时间价值
二、债券价值的评估
PPT文档演模板
第三章货币的时间价值
PPT文档演模板
第三章货币的时间价值
第一节 单利和复利
PPT文档演模板
第三章货币的时间价值
一、货币的时间价值
o 1、定义： o 货币的时间价值就是货币在时间推移中的增值能
力，或者是按资金使用时间的长短计算的报酬 o 这种报酬实际上就是指同一数量货币在不同时间
点上的价值差别，即利息 o 而这种货币（资金）的时间价值有两种形式：一
PPT文档演模板
第三章货币的时间价值
o 固定现金股利增长率的股票价值 (Gordon Growth Model)
式中g为现金股利的固定增长率。
PPT文档演模板
第三章货币的时间价值
o 利用EPS寻找g。Gordon模型提供了一种利用会计 数据估计现金股利增长率g，进而估计股票价值 的方法。EPS是公司可用于发放现金股利和再投 资的全部现金流量。
• K＝K＊＋IP • 关键取决于人们预期的通货膨胀率。
PPT文档演模板
第三章货币的时间价值
•结合这三种理论，债券收益曲线的形状取决于： •1、长期和短期市场的供需状况 •2、流动性偏好 •3、对未来通货膨胀的预期
PPT文档演模板
第三章货币的时间价值
第四节 货币时间价值的运用
PPT文档演模板
第三章货币的时间价值
• 长期利率并非总是如我们想像的那样大于短期 利率，而且在不同时间上，这两者之间的关系也会 有所差异。
PPT文档演模板
第三章货币的时间价值
• （一）债券收益率曲线的类型
• 1、正向收益率曲线
•r
•债券剩余期限
PPT文档演模板
第三章货币的时间价值
•2、反向收益率曲线
PPT文档演模板
第三章货币的时间价值
PPT文档演模板
第三章货币的时间价值
•（二）延期年金
• 延期年金是指最初的年金现金流不是发生在当前， 而是发生在若干期后。
PPT文档演模板
第三章货币的时间价值
•（三）固定增长年金 • 是指有规律地、按相同比例增长的现金流。
PPT文档演模板
第三章货币的时间价值
•（四）不等额现金流
• 对于不等额现金流，要将每期收付的现金流分别 复利计算到终期或者贴现到现在，然后求总求和。
PPT文档演模板
第三章货币的时间价值
2、流动性偏好理论
该理论认为，由于长期债券的力低于短期 债券，因而投资者一般喜欢购买短期债券而非 长期债券。因而在正常情况下的收益线的斜率 者会向上倾斜。
PPT文档演模板
第三章货币的时间价值
•3、预期理论
• 该理论认为，收益线的形状视投资者对未来通货 膨胀的预期而定。
PPT文档演模板
第三章货币的时间价值
•1元现值，10%各年单利、复利计算的终值比较
年限 1 2 3
5
10
20
30
50
单利终 1.1 1.2 1.3 1.5
2.0
3.0
4.0
6.0
值（元）
复利终 1.1 1.2 1.33 1.610 2.5937 6.7275 45.2593 117.391
值（元）
年金，是指每期期初有等额收付款项的年金，先付年金 与普通年金的惟一区别是收付款项发生的时间不同。
• 就终值计算来看，先付年金比普通年金多计算一 项利息；而就现值计算来看，先付年金又恰好比普通年 金少贴现一期利息。
PPT文档演模板
第三章货币的时间价值
o 年金终值系数表和现值系数表都是按照后付年金 编制的
是绝对数即利息，一种是相对数即利率
PPT文档演模板
第三章货币的时间价值
o 2、形成原因 o （1）通胀：使货币的购买力下降 o （2）风险：使人们愿意现在持有现金 o （3）个人消费偏好：使人们注重眼前消费 o （4）投资机会：使人们的货币有增值的可能
PPT文档演模板
第三章货币的时间价值
二、现值与终值
2.1、假设条件
o 1、债券的名义和实际支付额确定，即票面额和 市价确定。
o 2、通货膨胀的幅度可以精确地预测出来。
PPT文档演模板
第三章货币的时间价值
2.2、债券的基本估价公式
o 债券的价格有票面价格、内在价值和市场价格。 内在价值即我们要确定的债券价格，它是指在债 券的持有期所有预期货币收入的现值。预期货币 收入有两个来源：票面利息和票面额。
o 股票的价值为股票持有期内所得到的全部现金收 入（含股票转让的现金收入）的现值之和。
o 确定股票价值的一般公式
DIVt＝t期现金股利 n＝持有股票时领取现金股利的期 r＝股东要求的投资报酬 Pn＝股票出售时的价格
PPT文档演模板
第三章货币的时间价值
o 永久持有时股票价值公式 o 固定现金股利支付的股票价值
• 2、 IP通货膨胀溢酬，是指预期未来的通货膨胀率，而非 过去已发生的实际通货膨胀率，同时是一个平均预期值。 • 3、DRP违约风险溢酬。违约风险越大，则投资者所要求 的利率报酬就越高。 • 4、LP流动性溢酬。一般而言，在违约风险一期限风险皆 相同的情况下，最具变现力的金融资产与最不具变现力的金融 资产彼此间的利率差距约介于1%－2%之间。 • 5、MRP期限风险溢酬。期限越长的债券，期限风险越大。 它是对投资者利率变动风险的一种补偿。
o 普通年金（Ordinary Annuity），又称后付年 金，是指每期期末有等额的收付款项的年金。如 银行的零存整取存款。
PPT文档演模板
第三章货币的时间价值
1.1、普通年金终值的计算
普通年金终值是指一定时期内每期现金流的复利 终值之和。
PPT文档演模板
第三章货币的时间价值
•1.2、偿债基金
• 3、水平收益率曲线
PPT文档演模板
第三章货币的时间价值
•4、波动收益率曲线
PPT文档演模板
第三章货币的时间价值
•（二）利率期限结构理论
•1、市场区分理论
• 该理论认为，资金借贷双方对于贷款或贷款的 到期期间各有所好，因此收益线斜率取决于长短期资 金市场的资金供应情况。因而，在某一特定的时日， 长期利率会高于短期利率，此时债券收益线的斜率将 向上倾斜。反之，则向下倾斜。
o 要确定债券的价格需知道以下信息：（1）估计 的预期货币收入；（2）投资者要求的适当收益 率，即必要收益率，它一般是比照具有相同风险 程度和偿还期的债券的收益率得出。
PPT文档演模板
第三章货币的时间价值
•1、一次还本付息债券的估价公式 •2、一年付息一次债券的估价公式 •3、半年付息一次债券的估价公式
•二、利率水平的构成要素
• K＝K＊＋IP＋DRP＋LP＋MRP
•其中，K＊是实际无风险利率
•
IP为通货膨胀溢酬
•
DRP为违约风险溢酬
•
LP为流动性风险溢酬
•
MRP为期限风险溢酬
PPT文档演模板
第三章货币的时间价值
•具体而言：
• 1、K＊无风险利率，是纯粹利率，是指在预期通货膨胀 率为零时，无风险证券的平均利率。
第三章货币的时间价值
PPT文档演模板
2020/12/8
第三章货币的时间价值
本章主题
o 货币的时间价值是贯穿公司金融 活动始终的核心价值观。
o 本章将讲解货币时间价值原理及 及应用。
PPT文档演模板
第三章货币的时间价值
本章内容
o 第一节 单利、复利下现值、终值的计算 o 第二节 年金终值与年金现值 o 第三节 利率理论 o 第四节 货币时间价值的运用
PPT文档演模板
第三章货币的时间价值
•三、影响利率水平的因素
•1、供求关系
•r
PPT文档演模板
•资金
第三章货币的时间价值
•2、社会平均利润率 •3、宏观经济的发展形势 •4、消费的时间倾向性 •5、通货膨胀 •6、国家宏观经济政策
PPT文档演模板
第三章货币的时间价值
•四、利率期限结构
• 利率期限描述的是债券的收益率与其到期期间 的关系，亦即长短期利率间的关系。
o 折旧、租金、利息、保险金、养老金、退休金、 分期付款等都可以采用年金的形式。
o 年金按付款时间可分为后付年金（即普通年金）、 先付年金（即当期年金）两种形式。此外，还有 几种特殊的年金：永续年金、延期年金以及年金 的变化形式－不等额现金流等。
PPT文档演模板
第三章货币的时间价值
•
一、普通年金终值与现值的计算
•偿债基金是指为年金终值达到既定金额每期应 支付的年金数额。
•其中，
PPT文档演模板
•是年金终值系数的倒数，称为 偿债基金系数
第三章货币的时间价值
•1.3、普通年金现值计算
•称为年金现值系数，简记为PVIFAi,n
PPT文档演模板
第三章货币的时间价值
•二、先付年金的终值和现值的计算
• 先付年金（Annuity Due），又称当期年金、预付
o 现金股利发放率(Payout Ratio)＝DIV1/EPS1
o 再投资比率(Plowback Ratio)=1－Payout Ratio
PPT文档演模板
第三章货币的时间价值
o 权益收益率＝ROE＝EPS1/每股帐面净值 若企业不对外融资，则股东收益的增长只能来源于利用 留存收益所进行的再投资，有：
11
5