3多维非稳态对流扩散问题
- 格式:pdf
- 大小:318.26 KB
- 文档页数:31


一、扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间内,浓度不随时间变化dc/dt=0)单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx若原子平均跳动频率f, dt时间内跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间内两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从内壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉内脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离内溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C12)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。

非稳态扩散名词解释非稳态扩散:非稳态扩散又称自发过程、非平衡扩散,是不需要外界能量的作用就能自发进行的一类扩散过程。
自然界中的扩散多数是非稳态扩散。
本文主要介绍非稳态扩散。
⑴非稳态扩散定义:在无限时间内,随着流体通过的断面面积变化而产生的浓度变化,称为非稳态扩散。
它是依靠单位时间通过的总面积或所有截面的总通量来描述的。
⑵非稳态扩散过程的分类(1)化学平衡理论解释的平衡分布过程(2)熵值理论解释的平衡分布过程(量子力学认为所有物质的微观运动形式都服从统计规律)。
⑶非稳态扩散机理研究意义:⑴使对象更加复杂;⑵导致各个部分的性质发生改变;⑶导致结构变得更加复杂;⑷使人们可以获取到更加丰富的信息。
非稳态扩散:非稳态扩散又称自发过程、非平衡扩散,是不需要外界能量的作用就能自发进行的一类扩散过程。
自然界中的扩散多数是非稳态扩散。
非稳态扩散分为两大类:吸附扩散和分子扩散。
吸附扩散是分子或颗粒物质因受其他物质吸引,相互接近而引起的一种扩散过程。
其特点是扩散的浓度比在空气中低,扩散的传质系数比在空气中大。
分子扩散是指由于温度差或化学反应等引起的扩散。
其特点是扩散的浓度比在空气中高,扩散的传质系数比在空气中小。
⑷扩散过程与状态变化特点:①属于等温、等压、等体积过程;②扩散速率不受浓度差的影响;③扩散的方向性;④存在固定的扩散系数;⑤有特定的传质系数。
⑸浓度梯度与传质系数:在某一瞬时,物料中每一点上的浓度梯度是该点处各个浓度单位的相应值的连乘积。
传质系数k是单位时间内从扩散体系一侧通过单位截面积物料的量,也就是单位时间内每单位面积上的物料浓度梯度除以物料的体积V。
⑹不稳态扩散与稳态扩散:稳态扩散与不稳态扩散之间的区别是前者有外力推动。
而后者则没有,这是非稳态扩散与稳态扩散最根本的区别。
⑺稳态扩散与不稳态扩散的比较:在稳态扩散中,由于断面面积变化而产生的浓度变化可忽略,所以其分析的方法与其他类型的扩散相同。
而在不稳态扩散中,外力推动必须满足浓度变化的情况下才有意义,故其分析方法不同。

对流扩散方程解析解
《流体力学中的湍流扩散方程解析解》
一、什么是湍流扩散方程?
湍流扩散方程是描述物理流体扩散过程数学模型,是由流体力学中的湍流动力学概念推导出来的一种方程,是一种常用的偏微分方程。
它是一种描述在空间中湍流的扩散过程的数学方程,其目的是描述物质和能量在湍流中的传播。
二、湍流扩散方程的公式:
湍流扩散方程的公式为:
∂C/∂t = D∇2C
左侧的第一项是物质的局部变化率,t 代表时间;右侧的第一项用来描述物质在空间中的传播,D 为扩散系数,∇2C 为Laplace 算子。
三、湍流扩散方程的解析解:
1.快速波动方法:即快速 Fourier 过程,是一种快速处理湍流扩散方程的方法,其大致操作是用离散傅立叶变换把扩散方程转化为一个秩为 0
的傅立叶方程,然后使用傅立叶级数解决得出结果;
2.有限差分方法:给定的湍流扩散方程先采用有限的体积分解,即在时间及空间的二维平面上将扩散方程的计算区域划分成均匀的小单元,然后在每个区间内建立一个线性的有限差分矩阵,把扩散方程就变为简单的线性方程组;
3.格式方法:即 Finite Element 方法,用此方法可以把湍流扩散方程从不同的坐标方程中任意变换到球形坐标系,然后用有限元计算机程序解决;
4.积分方法:则是用数值积分的方法解决湍流扩散方程,包括 Runge-Kutta 方法、Adams 方法及其它积分的方法。
四、总结
湍流扩散方程是描述物理流体扩散过程的数学模型,是由流体力学中的湍流动力学概念推导出来的一种方程。
解决该方程有几种方法,即快速波动方法、有限差分方法、格式方法及积分方法。
以上是关于湍流扩散方程解析解的相关介绍,希望能够帮助到大家。

第四章扩散习题答案4-1解:本题为非稳态扩散问题,采用菲克第二定律。
由题意知,初始条件和边界条件为:t=0时,x>0 C = C 0; t ≥0时,x=0 C = C s ;t ≥0时,x=∞ C = C 0所以,可应用误差函数解来求解。
c(x,t)= C s -(C s - C 0)erf (Dtx2),其中,Cs=0, C 0=0.85%, 取C=0.8% 则:(C s –C)/( C s –C 0)= erf(Dt x2)∴(0-0.8%)/( 0-0.85%)= erf(3600*10*1.1211-x)∴erf(3600*10*1.1211-x)=0.94 查表知,3600*10*1.1211-x=1.33∴x=0.00053m=0.53mm∴ 应车去 0.53mm 的深度。
4-2解:本题为非稳态扩散问题,采用菲克第二定律。
由题意知,初始条件和边界条件为:t=0时,x>0 C = C 0; t ≥0时,x=0 C = C s ;t ≥0时,x=∞ C = C 0所以,可应用误差函数解来求解。
c(x,t)= C s -(C s - C 0)erf (Dt x 2),其中,Cs=1.1%, C 0=0 ①β=Dt x2=10*10*5.825.02-=0.33∴ erf(β)=0.3593C= C s -( C s – C 0) erf(β)=1.1%-1.1%×0.5393=0.705%②β= Dt x2=10*10*5.820.12-=0.66∴ erf(β)=0.6494C= C s -( C s -C 0) erf(β)=1.1%-1.1%×0.6494=0.386%③β= Dt x2=10*10*5.822.12-=0.79∴ erf(β)=0.7361C= C s -( C s -C 0) erf(β)=1.1%-(1.1%-0)×0.7361=0.29%④β= Dt x2=10*10*5.825.12-=0.98∴ erf(β)=0.8342C= C s -( C s -C 0) erf(β)=1.1%-(1.1%-0)×0.8342=0.18%⑤β= Dt x2=10*10*5.8222-=1.31∴ erf(β)=0.9361C= C s -( C s -C 0) erf(β)=1.1%-(1.1%-0)×0.9361=0.07%渗层内碳的浓度分布曲线如下:4-3解:本题为非稳态扩散问题,采用菲克第二定律。

非稳态扩散名词解释非稳态扩散是指物理、材料、化学及生物系统中的扩散过程,它对应于热力学的熵的非稳态增加。
它的本质是物质或能量从一个地方向另一个地方转移,以满足不均衡态的需要和条件。
而且它还可以在某些情况下产生有益的结果,从而改善系统的性能和功能。
非稳态扩散涉及一系列不同的现象,如传热、传热和传质等。
扩散在热力学中是指物质穿过温度或其他物理变量时,将温度或其他物理变量不均匀分布于各处的过程。
热扩散可以在物体表面和内部之间传递热量,而扩散系数描述的是热传递的强度。
扩散过程的速率取决于物质的种类、浓度和热能等。
热扩散是通过物体温度从高温区至低温区的传热而实现的,它对于定义散热器的有效性至关重要。
传质扩散是指在不同区域之间物质的扩散过程,即使温度在整个系统中是均衡的,也可以发生物质的扩散。
传质扩散的驱动力是物质的溶质浓度差异。
当物质的浓度在某一位置大于其他位置时,物质就会从高浓度区域流向低浓度区域。
这种可能会导致不良的影响,如污染和气味的扩散,因此应该尽可能多地阻止传质扩散。
生物系统中的非稳态扩散是指物质或信息在生物体之间以及内部生物体内部的扩散。
在生物体之间,细胞间信号传导是一种重要的非稳态扩散过程,其涉及受体细胞、信号转导蛋白与接受信号的分子等,其中都包含扩散的本质。
生物体内部的非稳态扩散是指细胞的活性蛋白的扩散,涉及到细胞间质和细胞膜的传递,从而影响各种细胞活性及细胞内功能的分布。
从上述内容可以看出,非稳态扩散是一种普遍存在的物理现象,它可以发生在物理、材料、化学和生物系统中,对于系统的功能性和性能有着重要的影响。
非稳态扩散涉及不同的现象,包括热传导、传热和传质扩散,以及生物体内部的细胞间信号传导和细胞内蛋白的扩散。
因此,了解非稳态扩散的机制和其对系统性能影响的理解,对于提高材料或生物系统的效率以及可靠性具有重要的意义。

一、扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间,浓度不随时间变化dc/dt=0)单位时间通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx若原子平均跳动频率f, dt时间跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C12)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。
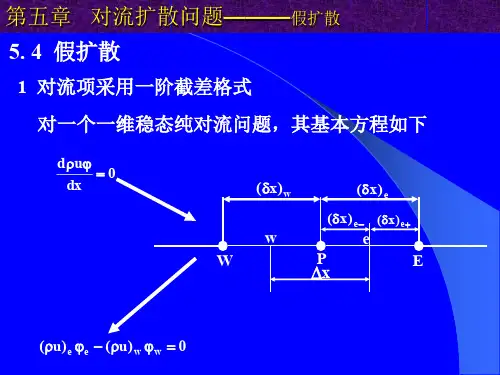


对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation)是在求解流体,如气体或液体的输运问题时需要使用的普通微分方程。
它表示物质被三种因素作用所引起的质量流动:对流、扩散和反应。
在本文中,我们将讨论对流扩散方程的解析解,以及它在工程中的重要作用。
首先,要理解对流扩散方程,我们必须从它的数学形式开始。
它可以用以下形式表示:$$frac{partial c}{partial t}+ vec{u} cdotabla c-Dabla^2 c=R$$在这里,$c$表示物质的浓度,$vec{u}$表示流体的速度,$D$表示物质的扩散系数,$R$表示反应的密度。
对流扩散方程的解析解是一种运用数学方法来求解这个方程的方法。
它主要是利用积分变换法(Integral Transform Method),将复杂的运动学问题转化为一组常微分方程求解。
解析解方法在解决一定类型的常微分方程时尤其有用,特别是当一个系统的边界条件是确定的时。
解析解的优势在于它可以提供直观的解,方便比较和评估结果,便于理解物理机理。
它也可以提供准确的结果,并可以用于组合的求解方法中。
在工程领域,对流扩散方程解析解的应用非常重要。
它可以被应用于温度或物质浓度输运,以及其他类似现象的计算。
例如,对流扩散方程可以用来模拟一定范围内扩散方式的热量传输,从而推测温度场分布;也可以用来模拟入口流场和出口的物质浓度的变化;它还可以用来描述各种物质在工程系统内的扩散问题。
再者,解析解方法也被广泛应用于制药行业。
对流扩散方程可以用来模拟药物在体内的运动,从而计算出最佳控制方案,以达到药物最佳疗效。
这不仅可以为药物分布模型提供依据,还可以用来估算药物组分以及药物与体细胞的相互作用等工程相关问题,从而帮助制药公司最大程度地提高药品安全性和疗效。
最后,对流扩散方程的解析解是一种非常有效的数学方法,它可以帮助我们更加清晰地理解流体输运问题,并可以提供准确可靠的结果。

流体的稳态与非稳态流体是一种特殊的物质形态,它具有流动性和变形性。
在许多物理和工程学领域,研究流体的稳态与非稳态是非常重要的。
稳态指的是流体在一定条件下保持恒定的流动状态,不随时间变化;非稳态则指流体的流动状态会随时间发生变化。
一、稳态流动稳态流动是指流体在空间和时间上保持恒定的流动状态。
稳态条件下,流体的速度场、压力场和密度场均不随时间变化,且在空间各点上保持恒定。
稳态流动通常发生在稳定的管道、河流以及一些工程设备中。
稳态流动具有以下特点:1. 守恒性质:在稳态条件下,流体在整个流动过程中,质量、动量和能量都保持不变。
这意味着在稳态流动中,流体在任何两点之间的质量流量、动量和能量传递都是平衡的。
2. 流速分布均匀:稳态流动时,流速在整个流场内分布均匀,没有明显的变化。
这是因为在稳态流动中,速度场保持不变,流体沿着固定路径流动,流速沿流动方向不发生变化。
3. 马克氏数恒定:在稳态流动中,流体的马克氏数为常数。
马克氏数是流体力学中一个重要的无量纲参数,它描述了流体的运动状态和热力学性质之间的关系。
二、非稳态流动非稳态流动是指流体在空间和时间上不断变化的流动状态。
非稳态流动常常发生在开关阀门、开始或停止流动等瞬态过程中,以及在激波、涡旋等复杂流动现象中。
非稳态流动具有以下特点:1. 时间变化:非稳态流动涉及流体的时间变化,即流速、压力和密度等在一段时间内发生变化。
在非稳态流动中,流场的速度和压力场随时间的推移而改变。
2. 波动与脉动:非稳态流动时,流体中的流速存在波动和脉动现象。
波动是指流速的周期性变化,脉动则是指流速的非周期性变化。
这些波动和脉动可能会导致流动的非均匀性和紊乱性。
3. 动量传播:在非稳态流动中,流体中的质量、动量和能量会随着流动的变化而传播,并在流场中发生扩散、对流和传导过程。
三、稳态与非稳态的区别稳态流动与非稳态流动之间存在明显的区别:1. 流动状态:稳态流动是持续且恒定的,而非稳态流动是变化的和不稳定的。
稳态扩散和非稳态扩散是物理学和化学领域中常用的术语,用来描述物质在空间中的扩散行为。
稳态扩散是指物质在均匀介质中的扩散过程,而非稳态扩散则是指物质在非均匀介质中的扩散过程。
本文将通过对稳态扩散和非稳态扩散的名词解释,解析其物理意义、数学表达和实际应用,帮助读者更好地理解这两个概念。
一、稳态扩散的名词解释1.1 稳态扩散的物理意义稳态扩散是指当物质在均匀介质中的浓度分布达到稳定状态时的扩散过程。
在稳态扩散中,物质的浓度分布不再发生变化,达到了动态平衡状态。
这种扩散过程通常以弥散系数来描述,可以用弥散方程进行数学建模,是一种重要的物质传输过程。
1.2 弥散系数的数学表达在稳态扩散中,物质的弥散系数是一个重要的物理参数,用来描述物质在均匀介质中扩散的能力。
它通常用符号D表示,是一个与时间和空间无关的常数。
弥散系数与介质的性质、温度和压力等因素有关,不同的物质在不同的介质中有不同的弥散系数。
1.3 稳态扩散的实际应用稳态扩散在化学工程、环境科学和生物医学等领域有着广泛的应用。
在化学工程中,稳态扩散常用来描述气体或液体在反应器中的传质过程;在环境科学中,稳态扩散被用来研究大气、水体和土壤中的污染物传播行为;在生物医学中,稳态扩散可用于分子在细胞内的扩散和运输研究。
二、非稳态扩散的名词解释2.1 非稳态扩散的物理意义非稳态扩散是指当物质在非均匀介质中的浓度分布随时间和空间发生变化的扩散过程。
在非稳态扩散中,物质的浓度分布不断改变,未达到动态平衡状态,通常需要考虑时间和空间的变化。
2.2 非稳态扩散的数学表达在非稳态扩散中,物质的扩散过程通常需要考虑时间和空间的变化,所以需要使用偏微分方程进行描述。
这类方程常常包括时间导数和空间导数,需要通过适当的数值或解析方法进行求解,得到物质浓度随时间和空间的变化规律。
2.3 非稳态扩散的实际应用非稳态扩散在材料科学、地球科学和生物学等领域有着重要的应用价值。
在材料科学中,非稳态扩散常用来研究材料中的晶体生长和变形过程;在地球科学中,非稳态扩散被用来描述地表和地下水体中的渗透和溶质迁移过程;在生物学中,非稳态扩散可用于描述细胞内物质的输运和信号传导过程。
非稳态扩散名词解释
非稳态扩散:一种“活跃”的化学扩散
在微观层面上,物质扩散体现为分子、原子或颗粒在不断变化的温度和压力的
作用下,穿过物质中的液体、气体,或者在它们的表面上的不断运动。
扩散,也可以在物理或化学上被描述为一种“运动”,而其中物质在运动过程中发生变化。
综上所述,扩散是宏观层面上和微观层面上不可缺少的一种运动过程。
在物理学中,扩散分为稳态扩散和非稳态扩散两类。
非稳态扩散是一种“活跃”的化学扩散,它会对它所经过部位的物态和选择性
形成一定的影响。
非稳态扩散过程中所演变出的物质的特性和空间散布情况反映出来,它的动力学特性一般由粒子的时空变化表征。
非稳态扩散一般不受外力的影响,它比一般的扩散更加活跃,所以在物质的多种化学活动中,它都起着重要的作用。
此外,非稳态扩散特别常见于微小体系,其会受到表面能和粒子相互作用的影响。
非稳态扩散比起稳态来说有较大的自主性,它能够更有效地传播激发信号,在传输消息中起到重要的作用。
它可以被用来驱动多时间尺度短、热休克信号跳跃或复杂化学反应等现象,发生在不稳定的体系中。
总而言之,非稳态扩散是一种多变现象,先于某一物质的变化而发生,而它的
演变轨迹由粒子的时空变化所誊描,它的影响力充满多样性,因为它可以驱动过多个时间尺度复杂的化学变化现象。
未稳态扩散可以说是化学活动中要有的不可缺
少的部分,它所提供的经历可以帮助研究者更深入地分析和预测化学系统的运行及其复杂程度。