当前位置：文档之家 › 电路第二章习题解答

电路第二章习题解答

  • 格式：doc
  • 大小：4.73 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

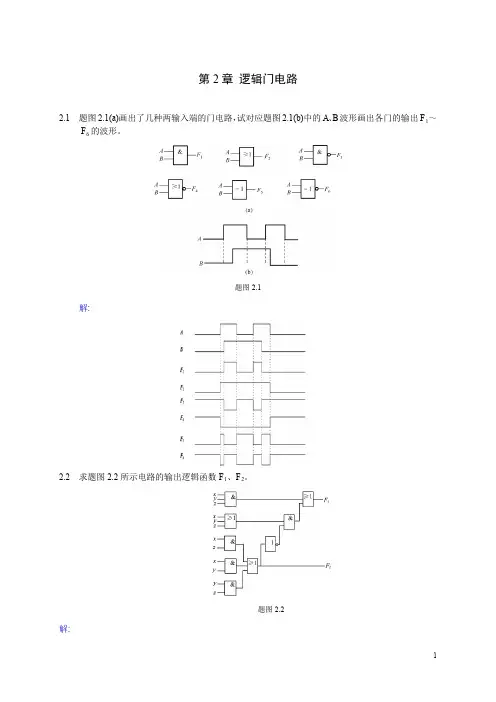
第2章 逻辑门电路-习题答案

第2章 逻辑门电路-习题答案

第2章逻辑门电路2.1 题图2.1(a)画出了几种两输入端的门电路，试对应题图2.1(b)中的A、B波形画出各门的输出F1～F6的波形。

题图2.1解:2.2 求题图2.2所示电路的输出逻辑函数F1、F2。

题图2.2解:2.3 题图2.3中的电路均为TTL门电路，试写出各电路输出Y1～Y8状态。

题图2.3解: Y1=0, Y2=0, Y3=Hi-Z, Y4=0, Y5=0, Y6=0, Y7=0, Y8=0.2.4 题图2.4中各门电路为CMOS电路，试求各电路输出端Y1、Y2和Y的值。

题图2.4解: Y1=1, Y2=0, Y3=0.2.5 6个门电路及A、B波形如题图2.5所示，试写出F1～F6的逻辑函数，并对应A、B波形画出F1～F6的波形。

题图2.5解：2.6 电路及输入波形分别如题图2.6(a)和2.6(b)所示，试对应A、B、C、x1、x2、x3波形画出F端波形。

题图2.6解：2.7 TTL与非门的扇出系数N是多少？它由拉电流负载个数决定还是由灌电流负载决定？解: N≤8 N由灌电流负载个数决定.2.8 题图2.8表示三态门用于总线传输的示意图，图中三个三态门的输出接到数据传输总线，D1D2、D3D4、…、D m D n为三态门的输入端，EN1、EN2、EN n分别为各三态门的片选输入端。

试问：EN信号应如何控制，以便输入数据D1D2、D3D4、…、D m D n顺序地通过数据总线传输（画出EN1～EN n 的对应波形）。

题图2.8解：用下表表示数据传输情况2.9 某工厂生产的双互补对称反相器（4007）引出端如题图2.9所示，试分别连接成：（1）反相器；（2）三输入与非门；（3）三输入或非门。

题图2.9解： (1) 反向器(2)与非门 (3)或非门2.10 按下列函数画出NMOS 电路图。

123()()()F AB CD E H G F A B CD AB CD F A B=+++=+++=⊕解：(1)(2) (3)2.11 将两个OC门如题图2.11连接，试写出各种组合下的输出电压u o及逻辑表达式。

电路第二章习题详解

电路第二章习题详解

P (4) 2 8W
6 . 求一端口网络的输入电阻RabA. 3ΩB. 4ΩC.7Ω
D. 10Ω
7. 求一端口网络的等效电阻。 i0
us +
+
含受控源， “外加电源”法 由定义式求取
u0
_
A. 1Ω
B. 3Ω
C. 4Ω
D. 5Ω
i0 i 2i
3i0 2i u0 0
i0 u0
习题
1、求图所示电路中电流值I ； 若电流源为10A，则I 又为多少？
+ 15V _
5A
I 5Ω
I 3A
2、求等效电阻Rab。
10Ω 10Ω a 10Ω 10Ω b b R a
R
R
R
R R
R
3、电路如图所示，求： 1) 电流I2 ； 2) 10V电压源的功率。 R1
I 2 2.5A
B. -2V
C. 2V
D.-12V
2 5 2 U ab 0
4. 一端口的短路电流Iab 。
Iab
A. 1A B. -1A
I ab 5 5
C. -5A
D. 5A
2
5. 求2A电流源发出的功率
+
D. 16W
A. 4W
B. -4W
C. -8W
3 2 10 u 0
u 4V
3I I a +
U _ b
Rab
2 3

书中的一道题： 求一端口的等效电阻Rab。
此处u1为开路电压
N
业精于勤，荒于嬉；
行成于思，毁于随。 ——韩愈
第2章习题
1. 求电路中电压U 。

数字电路 第2章习题解答

数字电路 第2章习题解答

2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。 a、b两图常用于扩展输入 端。 能否用于扩展TTL电路？ 为什么？
F2 A B C D E
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
不能用于扩展TTL电路。 在a图中，当C、D、E中 有低电平输入时，分立元 件与门输入到TTL电路的 电平已大于其VILmax，在逻 辑上可能相当于1，这样 分立元件与门已实现不了 “与”功能了。
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
不能用于扩展TTL电路。 在b图中，当C、D、E均 为低电平时，三个二极管 均截止，100kΩ电阻会使 TTL或非门输入相当于逻 辑1，因而，分立元件或 非门实现不了“或”运算 。
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
错误。 ⒉A=0，无论B、C取何值，AB=AC=0 ，故运算
错误。 ⒊1+B=1，A=B=1时，AB=1，故运算正确。
填空
采用5V电压供电的 CMOS门的抗干扰噪 声容限比5V电压供电的TTL门的抗干扰 噪声容限要（ 宽 ）。
TTL门带同类门的负载能力比CMOS门带 同类门的负载能力要（ 弱 ）。
F(A,B,C,D) =∑m（3，5，6，7，10） 约束条件：∑d（0，1，2，4，8）= 0。
用公式法化简函数 F ABCD ABD ACD
回答下列各题
•门电路组成的电路如图所示，请写出F1、 F2的逻辑表达式，当输入如图所示信号波 形时，画出F1、F2端的波形。
A
&
1
C
EN
TTL
&

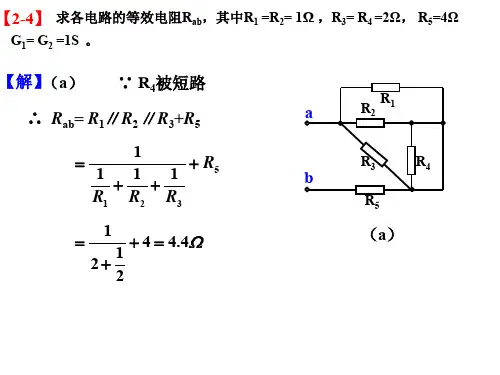
电路(第版)第二章习题答案

电路(第版)第二章习题答案

–
b 图（2）
Uab 4 Rab 4 5 20V
【2-13】图示电路中R1 =R3= R4 ，R2=2 R1， uc=4R1i1 ，利用电源的等效变换求电压 u10 。
【解】 在图（2）中：
ic

uc R2

4i1 R1 2 R1
2i1
R R2 /（ / R3 R4） R1
i1 R1 ① R3
+
+
uS
–
u10
–
R2
+
uc
–
R4
0
图（1）
u10 3i1R1
i1 R1 ① 3i1
uS i1R1 3i1R1 4i1R1
所以：
u10

3 4
uS
0.75uS
+
+ ic
uS
–
u10
–
0
R
图（2）
由电压源变换为电流源：
i 1
us
u
R
转换
u /R s
i
Ru
1'
由电流源变换为电压源：
Rab= (R1+ R3) ∥(R2+R4)
3 1.5
2
a
R1
R2
S
R3
b
R5
R4
（c）
桥形连接
惠斯通电桥
R1
I5
R3
R5
若： R1R4 = R2R3 则： I5 = 0
R2
R4
RS +
U_ S
电桥平衡
所以： 可将 R5 开路或短路。
【2-4】 求各电路的等效电阻Rab，其中R1 =R2= 1Ω ，R3= R4 =2Ω， R5=4Ω

电路分析第2章习题解析

电路分析第2章习题解析
R1= = 300
2-10如图示电路，已知R1=100，R2=200，R3=100，R4=50，R5=60，US=12V。求电流IAB。
题2-10图
解由图中R1和R3并联，R2与R4并联关系，可求出电流I
I= = A= 0.08A
再由分流关系，得
I3= I= 0.04A
I4= I= 0.064A
由KCL，得
电池内阻消耗（吸收）的功率P1为
P1=R1i2= 1 × 0.01W= 0.01W
电源产生的功率为
P=USi= 6 ×0.1W= 0.6W
或
P=P1+P2=（0.59 + 0.01）W= 0.6W
2-6图示为电池充电器电路模型。为使充电电流i=2A，试问R应为多少？
题2-6图
解由KVL有
= 2
解之
R= 2.91
所以等效电阻
Rab= =Rb+ ( 1 +)Re
2-21如图所示为一种T形解码网络。它具有将二进制数字量转换为与之成正比的模拟电压的功能，故常称之为数字模拟转换器。
（1）求网络的输入电阻Rin；
（2）求输入电压u1和电位uA、uB、uC、uD及输出电压u2。
题2-21图
解（1）求输入电阻Rin时，应从右端D处向左依次分段利用电阻的串、并联关系求之。观察可得
对于图(b)，因为
uAB= 6i3 + 4i+ 5 = 6V
故
i= 0.4A
2-4如图示电路，已知u=6V，求各电阻上的电压。
题2-4图
解设电阻R1、R2和R3上的电压分别为u1、u2和u3，由分压公式得
u1= ·u= × 6V= 1V
u2= ·u= × 6V= 2V

电路原理第二章课后习题答案

电路原理第二章课后习题答案

10 2 10
1R
Rx
r
r
Rx
Rx
7.5 7.5 ......
Rx
r
Rx
1'
3'
2'
(a)
2' (b)
1'
(a-1)
图 2.6
解：（a）设 R 和 r 为 1 级，则图题 2.6(a)为 2 级再加 Rx 。将 22 端 Rx 用始端
11 Rx 替代，则变为 4 级再加 Rx ，如此替代下去，则变为无穷级。从始端11 看等
30
40
30
40
30
40
30
40
R
R
(a 1)
(a 2)
由图(a-1)得：
R (30 40) 35 2
或由图(a-2)得
R 30 40 35 22
(b) 对图(b)电路，将 6Ω和 3Ω并联等效为 2Ω,2Ω和 2Ω并联等效为 1Ω,4Ω 和 4Ω并联等效为 2Ω，得图(b-1)所示等效电路：
Im1 20 Im2 6V m1 41 Im2 9.2V
答案 2.18
解：以节点①为参考点的各节点电压相对以节点④为参考点的节点电压降低了
U Un1 Un4 7V 。 则
Un1 0 Un2 Un2 U 5V 7V 2V Un3 Un3 U 4V 7V 3V
(1
(0.5 1) 0.5) Im1
Im1 (0.5 1) Im2 1 (0.5 1 2 1) Im2
Im3 5V 3 Im3
0
Im3 2I
由图可见，控制量和待求电流支路所在回路均只有一个回路电流经过，即
I m2 I ， Im1 Ix 。这样上式可整理成

第二章：电力电子习题解答

第二章：电力电子习题解答

第二章：电力电子习题解答第二章 整流电路习题及思考题１．单相半波可控整流电路对电阻负载供电，R ＝20Ω，U ＝100V ，求当α＝0°和60°时的负载电流Id ，并画出u d 与i d 波形。

解：当α＝0°时： ）（V .U .U d 451004504502=⨯==）（A ./RU I dd 2522045===当α＝60°时： ）（A ..U .U d 753325014502=+⨯=）（A ..RU I dd 691207533===u d 与i d 的波形见：教材43页图2－1。

２．图2－9为具有变压器中心抽头的单相全波可控整流电路。

问该变压器还有直流磁化问题吗？试说明：① 晶闸管承受的最大正反向电压为222U ；② 当负载为电阻或电感时其输出电压和电流的波形与单相全控桥时相同。

解：由图2－9图可以看出，在2U 正半周1VT 导通，负载电流由变压器次级上端流出，由中心抽头流入，当2U 负半周时2VT 导通，负载电流由B 次级下端流出由中心抽头流入，正负半周电流相等，但在铁芯中产生的磁势方向大小相等且方向相反，故变压器无直流磁化问题。

① 当1VT 导通时，在2u ＝22U 时，2VT 的阴极为22U ，而其阳极为－22U ，所以VT 承受的最大反压为222U 。

如果是阻感负载且电感是足够大时，当90=α，1VT 导通，2VT 的阴极电压为－22U 而其阳极电压为22，故其承受的最大正向电压为－222U 。

② 正半周1VT 导通，2U ud=，负半周2VT 导通2U u d =。

所以输出电压和电流的波形与单相全控桥时相同。

３．单相桥式全控整流电路，V U 1002＝，负载中Ｒ＝Ω2，Ｌ值极大，当30时，要求：① 作出du ，di 和2i 的波形；② 求整流输出平均电压dU 、电流dI ，变压器二次电流有效值2I ；③ 考虑安全裕量，确定晶闸管的额定电压和额定电流。

科学出版社电路理论第二章习题答案

科学出版社电路理论第二章习题答案

23 = 4KΩ+ 3 × = 4KΩ+ 3× 23KΩ = 73KΩ 3
2
2. 4、已知图2-67所示线性时不变电路由一个电 阻、一个电感和一个电容组成，其中：
i ( t ) = 10e − t − 20e −2t u1 ( t ) = −5e + 20e
−t
t≥0 t≥0
−2 t
若在t=0时电路的总储能W（0）=25J，试确定Z1,Z2,Z3 的性质及参数值。
线性时不变电阻有：
U R (0) = −10R (V )
Z1
u1
+(t) -
Z2
i1(t) Z3
(t ) = Ri1 (t ) = R(10e −t − 20e −2t ) UR
由KVL方程： U 1 (t ) + U R (t ) + U C (t ) = 0
Z2，Z3谁是电 阻、电容不能确 定。
∴U 1 (0 ) + U R (0 ) + U C (t ) = 0
∴U R t = 1.5 10e − t − 20e −2t
15V + −10R + O ⇒ R = 1.5Ω () ( ) −t −2 t ∴U R (t ) = 1.5(10e − 20e )
1 1 1 −t −2 t uc ( t ) = ∫ i1 ( t )dt = ∫ (10e − 20e )dt = ( −10e − t + 10e −2 t ) C C C
Is
I1
4Ω
IN
I2
6Ω I3
＋ I
uS =12V
＋ N uN －
R
－
解： 列l1的KVL方程： 方程： 的 方程

电工学-第二章习题答案

电工学-第二章习题答案

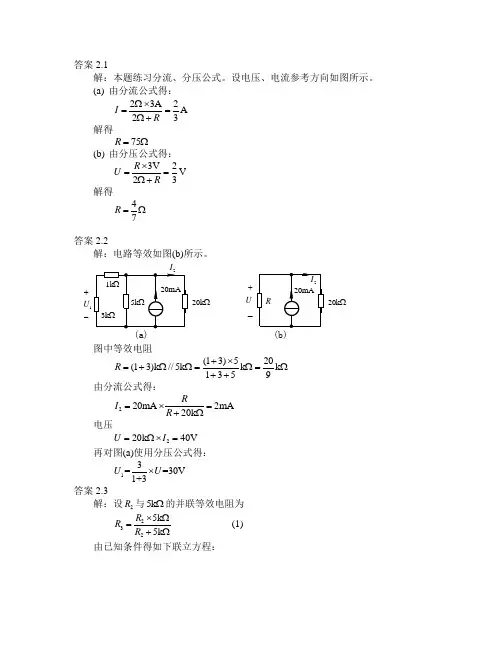
第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。

试求3I 和4I 。

4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。

R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。

Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。

I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。

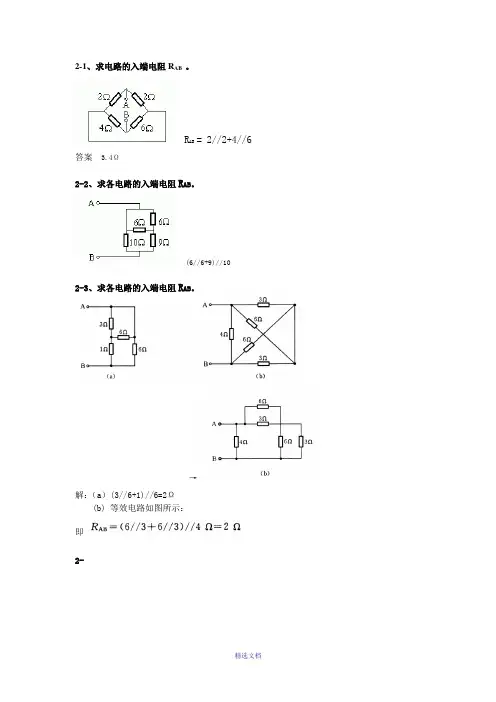
电路-第2章习题-电阻电路的等效变换

电路-第2章习题-电阻电路的等效变换

2-1、求电路的入端电阻R AB 。

R= 2//2+4//6AB答案 3.4Ω2-2、求各电路的入端电阻R AB。

(6//6+9)//102-3、求各电路的入端电阻R AB。

→解：（a）(3//6+1)//6=2Ω(b) 等效电路如图所示：即2-4、试求下图所示电路中的电流I。

答案-1.1A2-5、求图示电路中的电流i。

答案：- 0.1A2-6、电路如图所示，求B点的电位V B。

解：该电路图可以改变成如下图所示的形式2-7、电路如图所示，求电流I和电压U AB。

解：原电路可以等效变换为如下电路152-8、电路如图所示，求AB端的等效电阻R AB。

解：在AB端外加电源，使u、i对二端电路来说是关联参考方向。

由图可得：得到2-9、求图 (a) 和 (b) 所示两电路的输入电阻。

2-10、用电源等效变换法求图示电路中负载R L 上的电压U 。

12A5ΩR L+ -14V +-4Ω14-2Ω 2Ω2Ω2-11、化简为一个等效的电压源支路。

(a) (b) (c) (d)其中111R U I S S =，222R U I S S =，21S S S I I I +=，)(2121R R R R R S +=，S S S I R U =。

恒流源与恒压源的串联和并联两种情况(1) (2)2-12、化简图示电路。

(a) (b) (c) (d)2-13、在图（a ）所示电路中，已知V 12=S U ，Ω=31R ，A 5=S I ，Ω=62R ，试求2R 支路中的电流2I 。

(a) (b) (c)解： 3)5312(633)(12112=++=++=S S I R U R R R I A10；2-14、在图示电路中，N为一个实际的直流电源。

当开关S断开时，电压表读数为V1。

试求该直流电源N的电压源模型与电流源模型。

当开关S闭合时，电流表读数为A解：等效电路如图：，2-15、电路如图所示。

已知Ω=61R ，Ω=1.02R ，98.0=α，Ω=53R ，V U 9.4=。

电工学课后答案-第2章-电路的瞬态分析习题及答案

电工学课后答案-第2章-电路的瞬态分析习题及答案
u L (0) US R1 12 4 A 3 A
然后，根据，由换路后 (S 闭合时) 的电路求得
i1 ( 0 ) i2 (0 ) R2 R 1 R2 R1 R1 R 2 iL (0) iL (0) 6 46 4 46 3 A 1 .8 A 3 A 1 .2 A
iL
R2
6Ω
L
1H
返 回
第2章 电路的暂态分析
2.4.2图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL，并画出 其变化曲线。
i1
IS
S
i2
R3
7Ω
R1
24 A
R2
3Ω
uL
iL
1 .5 Ω
L
0 .4 H
a
S
b
R1
3Ω
2.4.3图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL，并说明是什么 响应。
uC U 0 e iC C

30 e U0 R
10
4
C
t
V 3e
10
4
R
t
uC
d uC dt

t
e

A
上一题 下一题
返 回练习题题集
上一页
第2章 电路的暂态分析
2.3.2在图所示电路原已处于稳态，在 t = 0 时，将开 关 S 闭合，试求响应 uC 和 iC，并说明是什么响应？
100 t
)V
e

15 e
mA
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析

第二章部分习题解答

第二章部分习题解答

第二章 习题2.1.13 在图中R 1= R 2 = R 3 = R 4 = 300Ω，R 5 = 600Ω， 试求开关 S 断开和闭合时a 、b 之间的等效电阻。

【解】开关 S 断开时：Ω=++=++=200600//)300300//()300300(//)//()(54231R R R R R R开关 S 闭合时：Ω=+=+=+=200600//)150150(600//]300//300300//300[//)]//()//[(54321R R R R R R2.3.5 在图示的电路中，求各理想电流源的端电压、功率及各电阻上消耗的功率。

【解】由KCL ，电阻R 1上电流： A I I I 11212=-=-=左边电流源：端电压（其与R1并联，电压相等）： V IR U 2020111=⨯== 功率 W U I P S 20201111=⨯==右边电流源：由KVL 可得端电压 V R I IR U 401022012212=⨯+⨯=+= 功率 W U I P S 40202222=⨯==电阻上消耗的功率：W R I P R 2020121211=⨯==,W R I P R 4010222222=⨯==2.3.9 试用电压源与电流源等效变换的方法计算图中2Ω电阻中的电流。

【解】对电路作等效变换，有：1Ω2A1Ω3Ω6Ω6V 12V 2ΩIR 1R 4R 5R 2R 3S3Ω6Ω2Ω I2A2V2A 2Ω－+ 1A10Ω20ΩR 1 R 2I 1I 2 2AU 1U 2I3Ω6Ω 2Ω I2A 2V 1Ω- + 6V ＋ － 1Ω计算电流：A I 122228=++-=2.4.2 试用支路电流法求图示电路中的各支路电流，并求三个电源的输出功率和负载电阻R L 取用的功率。

0.8Ω和0.4Ω分别为两个电压源的内阻。

【解】对节点A ，由KCL 有：I I I =++1021 对回路，由KVL ： I I 48.01201+=I I 44.01162+=联立求解得：I 1=9.38A ，I 2= 8.75A ，I =28.13A ， 三个电源的输出功率：W I I E P E 10558.021111=⨯-⨯=， W I I E P E 9844.022222=⨯-⨯=，W I IR I U P S L S AB IS 11251013.284=⨯⨯=⨯=⨯=负载电阻R L 取用的功率：W R I P L IS 316413.281613.28422=⨯=⨯== P L =3164W 。

《电工与电子技术基础》第2章正弦交流电路习题解答

《电工与电子技术基础》第2章正弦交流电路习题解答

67
（1）i= u Z
（2）I= U R + XC
（3）
I
=
R
U − jωC
（4）I= U Z
（7） I = − j U ωC
（5）U=UR+UC
（8）
I
=
j
U ωC
（6）U =UR + UC
解：在
R、C
串联电路中，总阻抗 Z
=
R
−
j
X
C
=
R
−
j
1 ωc
而 Z=
R2
+
X
2 C
I = U Z
L = XL =
8
= 25.5 (mH)
2πf 2 × 3.14 × 50
2.10 题 2.10 图中，U1=40V，U2=30V，i=10sin314t A，则 U 为多少？写出其瞬时值表 达式。
解：由电路图可知，电压 u1 与电流 i 同方向，而电压 u2 超前电流 i90º，所以
U=
U12
+
U
2.2 两个频率相同的正弦交流电流，它们的有效值是 I1=8A，I2=6A，求在下面各种情况 下，合成电流的有效值。
（1）i1 与 i2 同相。 （2）i1 与 i2 反相。 （3）i1 超前 i2 90º角度。 （4）i1 滞后 i2 60º角度。
解：（1） I = I1 + I2 = 8 + 6 = 14 （A）
− j4 2 − j2
=
2+
2j
+
− j4(2 + j2) (2 − j2)(2 + j2)
=3+
j (Ω)

电路基础(贺洪江)第2章习题解答

电路基础(贺洪江)第2章习题解答
u1=R1i
则
uS=2i+u1=2×3.5+5=12V
2-29在题2-29图所示电路中，已知uab=2V，求R=?
解应用KVL，得
uab=2u1+u1
u1= = V
由欧姆定律及KCL，得
i1= = A
i=1-i1=1- = A
R= = =3Ω
2-30求题2-30图所示两电路的输入电阻Rab。
解(a)采用外加电压源法求Rab。应用欧姆定律及KVL，得
将U=2I1代入上式，得
1.2I1=6
得
I1= =5A
受控源提供的功率为
P=0.8I1U=0.8I1(2I1)=0.8×2×52=40W
2-28在题2-28图所示电路中，已知uab=-5V，问电压源uS=?
解应用KVL，得
u1=4×0.5u1+uab
u1=-uab=-(-5)=5V
应用KCL，得
i=0.5u1+ =0.5×5+ =3.5A
解在图(a)中，按欧姆定律得
I= =2A
U=I×55=2×55=110V
在图(b)中，按分压关系得
U= =109.3983V
即电压表的读数为109.3983V。
在图(c)中，按欧姆定律有
I= =1.8333A
即电流表的读数为1.8333A。
由以上计算结果可知，电压表、电流表的内阻均使其读数小于其真实值，使测量的结果不够准确。为保证测量准确，电压表的内阻应尽量大一些，电流表的内阻应尽量小一些。
= =1.5385A
2-12求题2-12图所示电路中的u和i。
解由欧姆定律得
2-13计算题2-13图所示电路中的U和I。
解由分压关系得

电路与电子技术基础第2章习题参考答案

电路与电子技术基础第2章习题参考答案

《电路与电子技术基础》第二章参考答案
第3页
10Ω上的电压为 I×10=2.3×10=23(V) 因此 Us=23+Uab=23+21=44(V)
a 10Ω I Us 10Ω b 题图 2-4 习题 2-4 电路图 题图 2-5 I2 I3 I1 20Ω b -100V 习题 2-5 电路图 15Ω c +300V I1 R2 RL + 150V R1 20mA a 5mA
《电路与电子技术基础》第二章参考答案
第1页
习题二
2-1 求题图 2-1(a)中得 Uab 以及题图 2-1(b)中得 Uab 及 Ubc。 解： （1）图（a） ：
U 12 1 = = ( mA) 12k + 24k 36k 3 U 12 1 I2 = = = (mA) 36k + 36k 72k 6 U ab = U ac + U cb = I1 × 24k − I 2 × 36k I1 =
第2页
15Ω中流过的电流为
9 = 0.6(A ) 15 所以总电流为 I=I1+I2=0.6+0.3=0.9(A) 90Ω上的电压降为 0.9×90=81(V) 总电压为 U=81+9=90(V) 2-3 电路如题图 2-3 所示，若 10Ω两端得电压为 24V，求 R=? 解：已知 10Ω两端的电压为 24V，故 10Ω中的电流为 I1 =
a a + 6Ω 6Ω 6Ω U 6Ω 6Ω 6Ω 25A 6Ω c 题图 2-8 (b) 习题 2-8 电路图 (c) 6Ω 50A 6Ω 150V + 6Ω 150V + 6Ω c 150V + I + 150V 6Ω + a 300V 12Ω

电路分析第二章习题解答

电路分析第二章习题解答

i1
=
50 ＝5A R总
i2
=
−5 × 15 15 + 10
=
−3A
6．化简图题 2-6 所示各二端电路。
a
- 7Ω
3Ω
5V
+ 3A
1A b
（a）
a
3A
-
5V
+
+
2V
15Ω
-
b
（b）
a
a
-
5Ω
18Ω
5V
7Ω 12Ω
+
1A
10Ω
7A
+ 2A
10V -
20Ω
b
b
（c）
解： a) 电路等效为
图题 2-6
（d）
R
4Ω
25V
15Ω
6Ω 24Ω
4Ω
4Ω
图题 2-4
解： 原电路可等效为
R
I +
25V
i
+
u 15Ω
10Ω
Q P = 15 = i 2 ×15
根据分流公式
∴i = 1A u = 15V i = I × 10 = 2 I
15 + 10 5
∴ I = 5 i = 2.5A 2
R = 25 −15 = 4Ω 2.5
5．求图题 2-5 所示电路的i1和i2。
32Ω
6Ω
i1 4Ω
12Ω
50V 解： 原电路可等效为
15Ω i2 2Ω
图题 2-5
40Ω 30Ω 6Ω
i1
4Ω
50V
4Ω
15Ω
i2 2Ω
72Ω 5Ω
i1 4Ω

电路理论基础课后习题解析 第二章

电路理论基础课后习题解析 第二章

US
R I2
R I3
R
I1

3U S R
I2

I3

2U S R
I1 _
+ US
I1: I2 : I3=3:2:2
3.求电流I＝？
I 10A
2 6 2
10A
4
2 6
图(a)
Rab= 3
I
10
3 34

30 2

4.286
a 6
I
6
4 6
6
b 6
Rab
a
10A I 4 3

U 1

3I1
U 2I
Rab＝2
4.求输入电阻Rab＝？
2I
1 3 6
a
I
Rab
3
2I
b
8I
4
图(b)
U (1 3 2)I 4I 8I 10I
Rab＝10
a I 1 +
U
2I
_
b
8I
I 3 2I 2 4 I
b
3.求电流I＝？2A
1
3 6 1
6V 12V
I
4A 2
2A 1
I
2 1 2
图(b) 2A
1
1
3
I
8V
2V 1 I
6 1
2A
2A
2
2
2
I= 1A
4.求输入电阻Rab＝？ a I
U 1
Uo
I1
3I1
2U o 4
U 3U0
b
图(a)
2U0 4I1
I

电路分析第二章习题答案

电路分析第二章习题答案

K解:)(6A=闭合时: 总电阻Ω=+⨯+=463632R)(5.7430301ARI===此时电流表的读数为:)(55.7326361AII=⨯=+=2-2 题2-2图示电路，当电阻R2=∞时，电压表12V；当R2=10Ω时，解:当∞=2R时可知电压表读数即是电源电压SU..12VUS=∴当Ω=102R时,电压表读数:41210101212=⨯+=+=RURRRuS(V)Ω=∴201R2-3 题2-3图示电路。

求开关K打开和闭合情况下的输入电阻R i。

解：K )(18.60//(10Ω+=∴i RK)(8//30//(10Ω==∴i R2-4 求题2-3图示电路的等效电阻R ab 、R cd 。

解：电路图可变为：)(154882.214882.2148//82.21)4040//10//(80//30)(08.1782.294082.294082.29//40)80//3040//10//(40)(4020800)(8010800)(402080020201020202010123123Ω=+⨯==+=Ω=+⨯==+=Ω==Ω==Ω==⨯+⨯+⨯=cdab R R R R R 2-5 求题2-5图示电路的等效电阻 R ab 。

题2-59ΩΩΩ解：(a)图等效为：)(73.35687)25//(8Ω==⨯=+=∴ab R (b))(96325150Ω=+=+=∴ab R(c)图等效为：ΩΩ注意到10电阻可断去)(67.127147148)25//()410(8Ω=+⨯+=+++=∴ab R(d)图等效为：181818912+⨯=R)(2272//)36//1436//54()(722)(3612311223Ω=+=Ω==Ω==ab R R R R R2-6 题2-6图示电路中各电阻的阻值相等，均为R ，求等效R ab .(b)(a)解：e 、f 、g 电位点,所以 (a)图等效为：)]//()(//[)(R R R R R R R R R R R ab +++++++=R R R R R R R 45310//2]4//22//[2==+=(b)图等效为：])//()(//[)//()(R R R R R R R R R R R ab ++++++=RRR R R R R R R R 75.0433//)2//22//(2//22===+=2-7 化简题2-7图示各电路.245V 1028-836-解： （注：与电流源串联的元件略去，与电压源并联的元件略去）(a)图等效为：234-(b)图等效为：15-(d)图等效为：76-(e)图等效为：872- (f)图等效为：226V-2-8 用电源等效变换法求题2-8图示电路中负载R L 上的电压U .+ -14-2解：电路等效为：+ -7U+ -55-U+ -15-U+ -5+ -13+ -U+ -2.5)(3105.725.22V U =⨯+=2-9 题2-9图示电路.用电源等效变换法求电流i .3解：31A1A 55-)(412051055105A i -=-=++-=∴2-10 若题2-10图示电路中电流i 为1.5A,问电阻R 的值是多少?6-题2-10图解：流过R 的电流为i R =i -2=1.5-2= -0.5(A )，再利用电源等效变换，原电路等效为：21R其中3Ω//4Ω=Ω712，i ’=-1+0.5= -0.5(A )，)(712Ω=∴R 2-11 化简题2-11图示电路.12-u S-图解：(a)图等效为：4ba48-2a8-4ba2ba224-iab2 ab-11 ab(b)图：设端口电流为i ，则01=++i gu R u x x i gR R u x 111+-=∴ 原电路变为：aa1112111)1(gR R gR gR R +=+-+2-12 求题2-12图示电路中电流源和电压源提供的功率分别是多少?2Ω解：电流源发出功率为)(20102w P =⨯=原图可变为：ΩΩ2A2.21Ω2A)(21.221.11)9141142//(9141)2//76//221//(7//21)(7),(221),(73323233231312Ω=+=++=++=∴Ω=Ω=Ω=⨯+⨯+⨯=总R R R R)(32.452w R U P ==∴总总∴电压源发出的功率P =45.32-20=25.32(w ) 2-13 求题2-13图示电路a 、b 端的等效电阻R ab .Ω解：原电路等效为：1ΩΩ0.5ΩΩ)(35.22047)67//21(2Ω==+=∴ab R。

【精品】电路基础：第二章部分习题解.docx

【精品】电路基础：第二章部分习题解.docx

15Q> 00.4/列Lb 方程：13i + 5 x 1.4z + 10（z - 6）= 0z=2A2.5如图所示电路，试选一种树，确定基本割集方程求解电压u,如用节点法，你将选择哪一个节点作为参考点？试用一个节点方程求解电压it6V~O+ jG5A 200 [12V穴+II8Q4图2.5解：所选树为: 所选割集:电路基础：习题解答习题二24如图所示电路，试选一种树，确定基本回路，仅用一个基本回路方程求解电流匚图2.4解：所选树为:A = 1 Aj j3 =i —6所选基本回路:&4 = 20i 3 + 12故「3 = 1, U =20/3=20V2.6如图所示电路，已知电流z 1=2A, Z 2 = 1A 求电压％,电阻R 及电压源冷。

解：由KCL ：i2=ib+JZ3 + ‘4 =5la =h +5+S/；=/1+/2=3A由KVL： A R + 6i a = 28 =>2/? + 6x3 = 28 =>R = 5由KVL：3z c + 3 + 4Z2=Ri、3j. + 3 + 4 = 5 x 2 故i c= 1A由KVL：u s + 4i2 + 6i a = 28 => w s. = 6V由KVL：% _ 4 — 3 —比“ =0 二> % = 一7V2.7如图所示电路，各网孔电流如图所示，试列写出可用来求解该电路的网孔方程。

解：19匚+14一一4：= 一 10< ⑷A +2\i B +5： =-10一 4i A + 5i B + 12i c = 22.8如题图所示电路，设节点1, 2的电位分别为"如，试列解出可 用来求解该电路的节点方程。

解：原电路等价为: 对节点1, 2列节点方程，有:(1/3+1/1.2)妁一 1/3幻=1+5—4—1/3 绚+(1/3+1/4) W 2=4—2 — 1 化简可得：7 u } —2U 2= 12+2V图2.77 u2—4w( = 122.9如题图所示电路，求电压心。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章
1．求图题2-1所示二端电路的端口伏安特性。
图题2-1
解：
2．已知某两个二端电路的端口电压和电流取为非关联参考方向，它们的端口伏安特性分别为：（a） 、（b） ，求它们的等效二端电路。
解： 的等效二端电路为
的等效二端电路为
3．求图题2-3所示电路中从电压源看进去的等效电阻和电流i。
图题2-3
解：等效电阻
图题2-14
解：原电路可等效为
联立得：
15．图题2-15所示电路中，R1=1.5Ω，R2=2Ω，求电压u。
图题2-15
解：原电路等效为
联立得：
16．求图题2-16（a）、（b）所示二端电路的等效电阻Rab。
（a）（b）
图题2-16
解： 电路等效为
化简：
原电路因为 构成电桥
故连接两个 中间节点的 支路上电流为0
原电路可等效为
4．图题2-4所示电路中，已知15Ω电阻吸收的功率是15W，求R。
图题2-4
解：原电路可等效为
根据分流公式
5．求图题2-5所示电路的i1和i2。
图题2-5
解：原电路可等效为
化简为：
6．化简图题2-6所示各二端电路。
（a）（b）
（c）（d）
图题2-6
解： 电路等效为
=>
电路等效为
=>
电路等效为
图题2-10
解：原电路可等效为：
=>
得：
11．求图题2-11所示电路中的电流io。
图题2-11
解：原电路可等效为
=>
=>
列回路方程：
12．电路如图题2-12所示，求：
（a）电路中的uo；
（b）300V电压源产生的功率；
（c）原电路等效为
=>
列回路方程：
得
回到原电路：40 电阻上电流为 方向向左
根据节点定律：300V电源上电流 方向向右
300V电压源产生功率为
设 电阻上电压为 ，参考方向向下，列回路方程
设10A电流源上电压为 ，参考方向向下，在小回路中列回路方程
10A电流源产生功率为1300W
13．求图题2-13所示电路中的电流iR。
图题2-13
解：原电路可等效为
14．求图题2-14所示二端电路的端口伏安特性。
=>
电路等效为
=>
=>
7．求图题2-7所示电路中的u1、u2和i。
图题2-7
解：原电路等效为
列回路方程
回到原电路：根据节点定律：
8．求图题2-8所示电路中的u1。
图题2-8
解：原电路可等效为
=>
=>
9．利用电源变换求图题2-9所示电路中的i。
图题2-9
解：原电路可等效为
=>
=>
10．利用电源变换求图题2-10所示电路中的u1。
原电路等效为