二次函数图像的翻折变换

二次函数沿y轴翻折的条件是什么？
当二次函数的系数a小于0时，二次函数会沿y轴翻折。
例如，当二次函数为y = -x^2时，它会沿y轴翻折。图像如下：
[asy] unitsize(1 cm);
draw((-3,-9)--(-2,-4)--(-1,1)--(0,0)--(1,1)--(2,-4)--(3,-9),red); draw((-3,0)--(3,0));
draw((0,-9)--(0,3));

dot((0,0)); [/asy]
当a大于0时，二次函数不会沿y轴翻折。例如，当二次函数为y = x^2时，它
不会沿y轴翻折。图像如下：

[asy] unitsize(1 cm);
draw((-3,9)--(-2,4)--(-1,1)--(0,0)--(1,1)--(2,4)--(3,9),red); draw((-3,0)--(3,0));
draw((0,-9)--(0,3));

dot((0,0)); [/asy]
当a=0时，二次函数不是二次函数，而是一次函数。例如，当二次函数为y = 0
时，它不会沿y轴翻折。图像如下：

[asy] unitsize(1 cm);
draw((-3,0)--(-2,0)--(-1,0)--(0,0)--(1,0)--(2,0)--(3,0),red); draw((-3,0)--(3,0));
draw((0,-9)--(0,3));

dot((0,0)); [/asy]

二次函数图像的变换第一环节 【知识储备】一、二次函数图象的平移变换（1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其顶点平移到(,)h k .具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---； 2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++； 3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-；()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-；4. 关于顶点对称 2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-； ()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+． 5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．第二环节 【新知探究】【问题一】 平移变换求把二次函数y ＝x 2－4x ＋3的图象经过下列平移变换后得到的图象所对应的函数解析式：（1）向右平移2个单位，向下平移1个单位；（2）向上平移3个单位，向左平移2个单位。

二次函数的平移、翻折与旋转以及a、b、c符号问题1、抛物线的一般式与顶点式的互化关系：y＝ax2＋bx＋c————→y＝a(x＋b2a)2＋4ac－b24a2、强调利用抛物线的对称性进行画图，先确定抛物线的顶点、对称轴，利用对称性列表、描点、连线。

3、抛物线的平移抓住关键点顶点的移动；例题：1、（2015•龙岩）抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是．考点：二次函数图象与几何变换．分析：根据旋转的性质，可得a的绝对值不变，根据中心对称，可得答案．解答：解：将y=2x2﹣4x+3化为顶点式，得y=2（x﹣1）2+1，抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=﹣2（x+1）2﹣1，化为一般式，得y=﹣2x2﹣4x﹣3，故答案为：y=﹣2x2﹣4x﹣3．点评：本题考查了二次函数图象与几何变换，利用了中心对称的性质．2、（2015•湖州）如图，已知抛物线C1：y=a1x2+b1x+c1和C2：y=a2x2+b2x+c2都经过原点，顶点分别为A，B，与x轴的另一交点分别为M，N，如果点A与点B，点M与点N都关于原点O成中心对称，则称抛物线C1和C2为姐妹抛物线，请你写出一对姐妹抛物线C1和C2，使四边形ANBM恰好是矩形，你所写的一对抛物线解析式是和．考点：二次函数图象与几何变换．专题：新定义．分析：连接AB，根据姐妹抛物线的二次项的系数互为相反数，一次项系数相等且不等于零，常数项都是零，设抛物线C1的解析式为y=ax2+bx，根据四边形ANBM恰好是矩形可得△AOM是等边三角形，设OM=2，则点A的坐标是（1，），求出抛物线C1的解析式，从而求出抛物线C2的解析式．解答：解：连接AB，根据姐妹抛物线的定义，可得姐妹抛物线的二次项的系数互为相反数，一次项系数相等且不等于零，常数项都是零，设抛物线C1的解析式为y=ax2+bx，根据四边形ANBM恰好是矩形可得：OA=OM，∵OA=MA，∴△AOM是等边三角形，设OM=2，则点A的坐标是（1，），则，解得：则抛物线C1的解析式为y=﹣x2+2x，抛物线C2的解析式为y=x2+2x，故答案为：y=﹣x2+2x，y=x2+2x．w W w .x K b 1.c o M点评：此题考查了二次函数的图象与几何变换，用到的知识点是姐妹抛物线的定义、二次函数的图象与性质、矩形的判定，关键是根据姐妹抛物线的定义得出姐妹抛物线的二次项的系数、一次项系数、常数项之间的关系．3、（2015•绥化）把二次函数y=2x2的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为．考点：二次函数图象与几何变换．分析：直接根据“上加下减，左加右减”的原则进行解答．解答：解：由“左加右减”的原则可知，将二次函数y=2x2的图象向左平移1个单位长度所得抛物线的解析式为：y=2（x+1）2，即y=2（x+1）2；由“上加下减”的原则可知，将抛物线y=2（x+1）2向下平移2个单位长度所得抛物线的解析式为：y=2（x+1）2﹣2，即y=2（x+1）2﹣2．故答案为：y=2（x+1）2﹣2．点评：本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．4、（2015•岳阳）如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是．（写出所有正确结论的序号）①b＞0②a﹣b+c＜0③阴影部分的面积为4④若c=﹣1，则b2=4a．考点：二次函数图象与几何变换；二次函数图象与系数的关系．分析：①首先根据抛物线开口向上，可得a＞0；然后根据对称轴为x=﹣＞0，可得b＜0，据此判断即可．②根据抛物线y=ax2+bx+c的图象，可得x=﹣1时，y＞0，即a﹣b+c＞0，据此判断即可．③首先判断出阴影部分是一个平行四边形，然后根据平行四边形的面积=底×高，求出阴影部分的面积是多少即可．④根据函数的最小值是，判断出c=﹣1时，a、b的关系即可．解答：解：∵抛物线开口向上，∴a＞0，又∵对称轴为x=﹣＞0，∴b＜0，∴结论①不正确；∵x=﹣1时，y＞0，∴a﹣b+c＞0，∴结论②不正确；∵抛物线向右平移了2个单位，∴平行四边形的底是2，∵函数y=ax2+bx+c的最小值是y=﹣2，∴平行四边形的高是2，∴阴影部分的面积是：2×2=4，∴结论③正确；∵，c=﹣1，∴b2=4a，∴结论④正确．综上，结论正确的是：③④．故答案为：③④．点评：（1）此题主要考查了二次函数的图象与几何变换，要熟练掌握，解答此类问题的关键是要明确：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．（2）此题还考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确：①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）③常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．答案：。

二次函数中考所占分值18分。

二次函数在中考中常常以压轴题的形式出现，常常占分值十八分，主要考查二次函数的解析式中的一般式如何通过配方成为顶点式，继尔求顶点坐标，对称轴，画出二次函数的图像，求二次函数与x轴的交点坐标，与y轴的交点坐标，还求抛物线的开口方向。

学好函数还是有诀窍的，首先要掌握好下面六个考点。

(一）二次函数的定义一般地，如果y=ax^2+bx+c(a，b，c是常数，a≠0)，那么y叫做x的二次函数.其中x是自变量，a,b,c分别为函数表达式的二次项系数、一次项系数和常数项。

二次函数的有三种表达式：(1)一般式：y=ax^2+bx+c(a，b，c是常数，且a≠0)；(2)顶点式：y=a 〖"(x-h)" 〗^2+k(a≠0)，它直接显示二次函数的顶点坐标是(h，k)；(3)交点式：y=a(x-x1)(x-x2)(a≠0)，其中x1，x2是图像与x轴交点的横坐标。

（二）二次函数的图像和性质抛物线是轴对称图形，对称轴为直线x=-b/2a；对称轴与抛物线唯一的交点为抛物线的顶点P。

特别得，当b=0时，抛物线的对称轴是y轴（即直线x=0）。

抛物线有一个顶点P，坐标为P[-b/2a，(4ac-b)/4a]；当-b/2a=0时，P在y轴上；当Δ=b-4ac=0时，P在x轴上。

二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|越大，则抛物线的开口越小。

一次项系数b和二次项系数a 共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b 异号时（即ab＜0），对称轴在y轴右。

常数项c决定抛物线与y轴交点；抛物线与y轴交于（0，c）。

（三）二次函数图像的平移、旋转和翻折二次函数顶点式的平移的步骤：a.将抛物线解析式转化为顶点式y=a(x-h)^2+k,确定其顶点坐标；b.保持抛物线的形状不变，平移顶点坐标(h,k)即可。

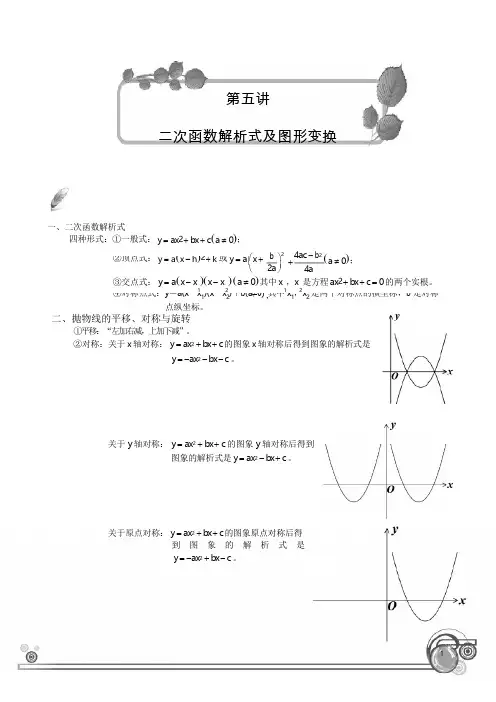
②顶点式： y = a (x - h )2 + k 或 y = a x +⎪ + ④对称点式：y ＝a(x －x 1)(x －x 2)＋b (a ≠0) 其中 x 1，x 2 是两个对称点的横坐标，b 是对称第五讲二次函数解析式及图形变换一、二次函数解析式四种形式：①一般式： y = ax 2 + bx + c (a ≠ 0)；⎛ ⎝b ⎫2 2a ⎭4ac - b 2 (a ≠ 0)； 4a③交点式： y = a (x - x )(x - x ) (a ≠ 0) 其中 x ，x 是方程 ax 2 + b x + c = 0 的两个实根。

1 2 1 2， 点纵坐标。

二、抛物线的平移、对称与旋转①平移：“左加右减，上加下减”。

②对称：关于 x 轴对称： y = ax 2 + b x + c 的图象 x 轴对称后得到图象的解析式是y = -ax 2 - b x - c 。

关于 y 轴对称： y = ax 2 + b x + c 的图象 y 轴对称后得到图象的解析式是 y = ax 2 - b x + c 。

关于原点对称： y = ax 2 + b x + c 的图象原点对称后得到 图 象 的 解 析 式 是 y = -ax 2 + b x - c 。

1．求二次函数 y = ax 2 + b x + c 与直线 y = kx + m 的交点，联立方程组 ⎨ 求解。

2．求二次函数 y = a x 2+ b x + c 与 y = a x 2+ b x + c 的交点，联立方程组 ⎨ 求解。

⎧⎪ y = a x 2 + b x + c ⎪⎩ y = a x 2 + b x + c ⑶（2007 朝阳二模）已知抛物线 y = ax 2 + b x(a ≠ 0) 的顶点在直线 y = -x - 1 上，当且仅当 ⑵请探索：是否存在二次项系数的绝对值小于 的整点抛物线？若存在，请写出其中一条抛物线三、二次函数与一元二次方程⎧ y = ax 2 + bx + c ⎩ y = kx + m1 1 1 1 1 12 2 2 2 2 2板块一 二次函数解析式【例1】 ⑴ 下列说法不正确的是（）A ．抛物线 y = ax 2 + b x - 3 与 y 轴的交点为 (0 ，- 3)B ．抛物线 y = ax 2 - 2ax + a 2 - 1 的对称轴为 x = 1C ．抛物线 y = ax 2 - a (m + 1)x + ma 与 x 轴的交点为 (m ，0)和 (1，0)D ．抛物线 y = a (x + π )2 - x 的顶点坐标为 (-π ，- x )⑵（2009 三帆单元测试）已知抛物线 y = ax 2 + bx + c 经过点 A (-1，0)，且经过直线 y = x - 3 与x 轴的交点 B 及与 y 轴的交点 C ，则抛物线的解析式为。

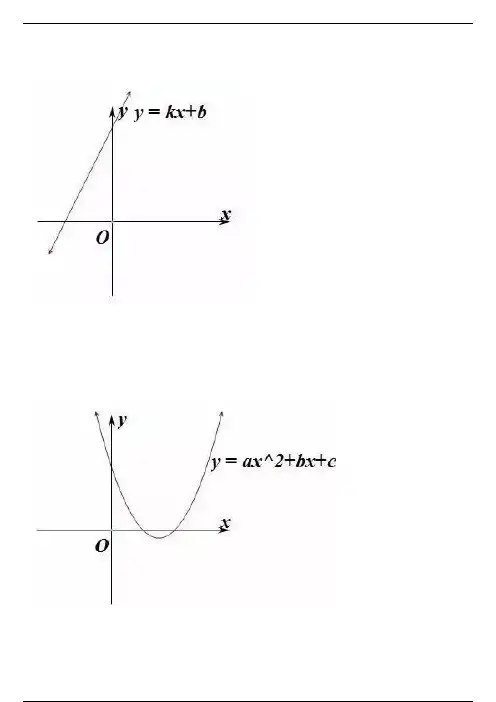
基本初等函数的图像1.一次函数性质： 一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减 2.二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3.反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的6.对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

7. 幂函数性质：先看第一象限，即 x>0 时，当 a>1 时，函数越增越快；当0<a<1 时，函数越增越慢；当 a<0 时，函数单调递减；然后当x<0 时，根据函数的定义域与奇偶性判断函数图像即可。

8. 正弦函数、余弦函数、正切函数函数图像的变换 1 平移变换（1）水平平移： 函数 y = f（x + a）的图像可以把函数 y =f（x）的图像沿x轴方向向左（a＞0）或向右（a＜0）平移｜a｜个单位即可得到； （2）竖直平移： 函数 y = f（x） + a 的图像可以把函数 y =f（x）的图像沿x轴方向向上（a＞0）或向下（a＜0）平移｜a｜个单位即可得到。

2 对称变换（1）函数 y = f（-x） 的图像可以将函数 y = f（x）的图像关于y轴对称即可得到； （2）函数 y = - f（x） 的图像可以将函数 y =f（x）的图像关于x轴对称即可得到；（3）函数 y = - f（-x） 的图像可以将函数 y =f（x）的图像关于原点对称即可得到；3 翻折变换（1）函数 y =｜ f（x）｜ 的图像可以将函数 y =f（x）的图像的x轴下方部分沿x轴翻折到x轴上方，去掉x轴下方部分，并保留 y =f（x）的x轴上方部分即可得到；（2）函数 y = f（｜x｜） 的图像可以将函数 y =f（x）的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y =f（x）在y轴右边部分即可得到。

初中数学知识归纳二次函数的性质与变形初中数学知识归纳：二次函数的性质与变形二次函数是初中数学中重要的一个概念，它在解决实际问题中有着广泛的应用。

在学习二次函数时，我们需要了解其性质和变形。

通过归纳与总结，本文将介绍二次函数的性质与变形，帮助读者更好地掌握这一内容。

一、二次函数的性质1. 对称轴与顶点二次函数的图像是一条抛物线，它的对称轴是通过抛物线顶点的一条线。

对称轴与x轴垂直，是抛物线的镜像轴。

顶点是抛物线的最低点或最高点，也是对称轴上的点。

2. 开口方向与最值二次函数的开口方向取决于二次项的系数，当二次项系数大于0时，抛物线向上开口，最值为最小值；当二次项系数小于0时，抛物线向下开口，最值为最大值。

3. 零点与交点二次函数的零点是使函数值为0的自变量值。

可以通过求解二次方程来计算零点。

当二次函数与x轴相交时，交点即为零点。

二、二次函数的变形1. 平移变换平移变换改变了函数图像的位置，有以下两种情况：a. 水平平移：将二次函数的图像沿着x轴平移，平移的距离取决于平移向量的值。

当平移向量为正时，图像左移；当平移向量为负时，图像右移。

b. 垂直平移：将二次函数的图像沿着y轴平移，平移的距离取决于平移向量的值。

当平移向量为正时，图像上移；当平移向量为负时，图像下移。

2. 缩放变换缩放变换改变了函数图像的形状和大小，有以下两种情况：a. 水平缩放：将二次函数的图像沿着x轴缩放，缩放的比例由缩放因子确定。

当缩放因子大于1时，图像变宽；当缩放因子在0和1之间时，图像变窄。

b. 垂直缩放：将二次函数的图像沿着y轴缩放，缩放的比例由缩放因子确定。

当缩放因子大于1时，图像变高；当缩放因子在0和1之间时，图像变矮。

3. 翻折变换翻折变换改变了函数图像关于x轴或y轴的对称性，有以下两种情况：a. x轴翻折：将二次函数的图像沿着x轴翻折，改变了抛物线的开口方向。

原本向上开口的抛物线变为向下开口，反之亦然。

b. y轴翻折：将二次函数的图像沿着y轴翻折，改变了抛物线的左右关系。

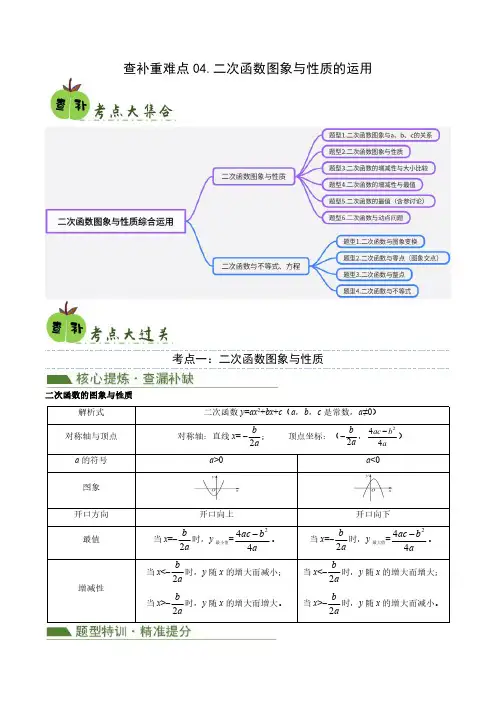
查补重难点04.二次函数图象与性质的运用考点一：二次函数图象与性质二次函数的图象与性质解析式二次函数y =ax 2+bx +c （a ，b ，c 是常数，a ≠0）对称轴与顶点对称轴：直线x =–2b a ；顶点坐标：（–2b a ，244ac b a -）a 的符号a >0a <0图象开口方向开口向上开口向下最值当x =–2b a 时，y 最小值=244ac b a-。

当x =–2b a 时，y 最大值=244ac b a -。

增减性当x <–2b a 时，y 随x 的增大而减小；当x >–2b a 时，y 随x 的增大而增大。

当x <–2b a 时，y 随x 的增大而增大；当x >–2b a 时，y 随x 的增大而减小。

题型1.二次函数图象与a 、b 、c 的关系1）抛物线开口的方向可确定a 的符号：抛物线开口向上，a ＞0；抛物线开口向下，a ＜02）对称轴可确定b 的符号（需结合a 的符号）：对称轴在x 轴负半轴，则ab ＞0；对称轴在x 轴正半轴，则ab ＜0（即：左同右异）3）与y 轴交点可确定c 的符号：交于y 轴负半轴，则c ＜0；交于y 轴正半轴，则c ＞04）特殊函数值符号（以x =1的函数值为例）：若当x =1时，若对应的函数值y 在x 轴的上方，则a+b+c ＞0；若对应的函数值y 在x 轴上方，则a+b+c =0；若对应的函数值y 在x 轴的下方，则a+b+c ＜0；例1.（2021·江苏宿迁·中考真题）已知二次函数2y ax bx c =++的图像如图所示，有下列结论：①0a ＞；②24b ac -＞0；③40a b +=；④不等式21ax b x c +-+（）＜0的解集为1≤x ＜3，正确的结论个数是（）A ．1B ．2C ．3D ．4变式1．（2023年湖北省黄冈市中考数学真题）已知二次函数2(0)y ax bx c a =++<的图象与x 轴的一个交点坐标为(1,0)-，对称轴为直线1x =，下列论中：①0a b c -+=；②若点()()()1233,,2,,4,y y y -均在该二次函数图象上，则123y y y <<；③若m 为任意实数，则24am bm c a ++≤-；④方程210ax bx c +++=的两实数根为12,x x ，且12x x <，则121,3x x <->．正确结论的序号为（）A ．①②③B ．①③④C ．②③④D ．①④变式2．（23-24九年级·江苏宿迁·阶段练习）已知二次函数2(0)y ax bx c a =++<的图象与x 轴的一个交点坐标为(1,0)-，对称轴为直线1x =，下列结论中：①0a b c -+=；②若点1(3,)y -，2(2,)y ，3(4,)y 均在该二次函数图象上，则123y y y <<；③若m 为任意实数，则24am bm c a ++≤-；④若221122ax bx ax bx +=+且12x x ≠，则122x x +=-；⑤方程210ax bx c +++=的两实数根为1x ，2x ，且12x x <，则11x <-，23x >．其中正确的结论个数是()A ．1个B ．2个C ．3个D ．4个题型2.二次函数图象与性质熟练掌握二次函数的图象与性质，运用相关知识解答即可。

二次函数解析式及其图象变换模块一 二次函数的解析式知识导航1. 一般式： y ＝ax 2＋bx ＋c (a ≠0)若已知条件为二次函数图象上三点的坐标，通常先设抛物线的解析式为一般式，列出关于a 、b 、c 的方程，求出a 、b 、c 的值，就可以得到二次函数解析式．2. 顶点式：y ＝a （x －h ）2＋k ．若已知顶点坐标、对对称轴、最大值或最小值，通常先设抛物线的解析式为顶点式，再列出方程（组）求待定系数．3. 交点式：y ＝a （x －x 1)(x －x 2)若已知与x 轴的两交点（x 1，0)、(x 2，0），通常先设抛物线的解析式为两点式，再列出方程（组）求待定系数.（仅用于选项或打草稿）例1：（1）一个抛物线经过（0，0）、（－1，1）、（1，9）三点，求这个抛物线的解析式．（2）一个抛物线的顶点为（3，3）、且经过点（2，1）求这个抛物线的解析式．（3）一个抛物线经过（－1，0）、（3，0）、（1，4）三点，求这个抛物线的解析式．练习：（1）一个抛物线经过（－1，20）、（0，8）、（2，8）三点，求这个抛物线解析式．（2）一个抛物线经过（2，1）、（1，3）两点且对称轴为x ＝－21，求这个抛物线解析式． （3）一个抛物线经过（－1，3）、（1，3）、（2，6）三点，求这个抛物线的解析式．例2：（1）已知抛物线y ＝a （x ＋2）2－1交x 轴于A 、B 两点（A 点在B 点的左边）且AB ＝2，求抛物线解析式．（2）已知二次函数y ＝ax 2＋4a x ＋c 的最大值为4，且图象过点（－3，0），求二次函数的解析式．练习：（1）已知二次函数y ＝ax 2＋bx ＋c 图象的对称轴是直线x ＝1，且图象过点A （3，0）和B （－2，5），求函数的解析式．（2）已知二次函数y ＝52x 2＋bx ＋c 图象与y 轴交于A （0，3）与x 轴交于B （1，0），则此抛物线的解析式为？例3：如图，抛物线y ＝ax 2－5ax ＋4经过△ABC 的三个顶点，点A 、C 分别在x 轴、y 轴上，AC ＝BC ，此抛物线的解析式?练习：如图，抛物线y ＝ax 2＋4ax ＋b 交x 轴于A 、B 两点，交y 轴于C 点，直线y ＝－x －1过点A ，与抛物线交于点D ，且CD//x 轴，求抛物线的解析式．例4：（1）已知抛物线y ＝x 2＋mx －4m 总经过一个定点P ，求出点P 的坐标．（2）已知抛物线y ＝（m ＋2）x 2－（m ＋1）x －2总经过两个定点，求出两个定点坐标．（3）已知抛物线y ＝mx 2－2mx －3m 总经过两个定点，求出这两个定点坐标．练习：已知抛物线y ＝（m ＋1）x 2－4m ）x ＋4总经过两个定点，求出这两个定点坐标．例5 （1）不论m取任何实数，抛物线y＝x2＋2mx＋m2＋m－1的顶点都在一条直线上，则这条直线的函数解析式为？（2）不论m取任何实数，抛物线y＝x2－2mx＋2m2＋3m＋1的顶点都在一条抛物线上，则这条抛物线的函数解析式为？练习：不论m取任何实数，抛物线y＝x2－2mx＋m2＋m＋3的顶点都在一条直线上，则这条直线的函数解析式为？模块二二次函数的图象变换知识导航我们已经从y＝ax2、y＝ax2＋k、y＝a（x－h）2＋k的图象和性质知道了几种二次函数解析式之间的平移关系，同样的我们可以得到作对称、旋转变换的二次函数解析式之间的关系．1. 关于x轴对称因为顶点（h，k）关于x轴对称后的点为（h，－k），此时开口的方向改变，所以二次函数y＝a（x －h）2＋k关于x轴对称后得到的解析式是y＝－a（x－h）2－k．2. 关于y对称因为顶点（h，k）关于y轴对称后的点为（－h，k），此时开口的方向不变，所以二次函数y＝a（x－h）2＋k关于x轴对称后得到的解析式是y＝－a（x＋h）2＋k．3. 关于顶点对称（180°旋转）此时顶点不变，但开口的方向改变，所以y＝a（x－h）2＋k关于顶点对称后，得到的解析式是y＝－a （x－h）2+k．4. 关于原点对称（180°旋转）因为顶点（h，k）关于原点对称后的点为（－h，－k），此时开口的方向改变，所以二次函数y＝a（x －h）2＋k关于x轴对称后得到的解析式是y＝－a（x＋h）2－k．例6 已知二次函数解析式y＝x2＋2x－3，求将改二次函数的图象作如下变换后的解析式．（1）沿y轴向上平移1个单位长度；（2）沿y轴向上平移2个单位长度；（3）沿x轴向左平移3个单位长度；（4）沿x轴向右平移4个单位长度；（5）关于x轴对称；（6）关于y轴对称；（7）关于顶点对称；（8）关于原点对称；练习（1）将抛物线y＝－x2＋2x－3先向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式．（2）将抛物线y＝x2－x－4沿x轴翻折，求翻折后的抛物线的解析式．（3）将抛物线y＝x2－2x－1绕它的顶点旋转180°，求旋转后的抛物线的解析式．例7：：（1）已知抛物线y＝（x＋1）2－4，将其沿直线x＝1翻折，求翻折后的抛物线的解析式．（2）求抛物线y＝－x2＋4x－7关于直线y＝－2对称的抛物线的解析式．（3）在平面直角坐标系中，将抛物线y＝x2＋2x＋3绕着它与y轴的交点旋转108°，求旋转后的解析式.练习：求抛物线y＝－x2＋2x＋3关于（2，3）对称的抛物线解析式.例8(1)在平面直角坐标系中，将抛物线y＝x2－x－6向上（下）或向左（右）平移m个单位，使平移后的抛物线恰好经过原点，则m的最小值为.（2）已知y＝2x2的图象是抛物线，若抛物线不动，把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是.（3）如图，把抛物线y＝x2沿直线y＝x平移2个单位后，其顶点在直线上的A处，则平移后的抛物线的解析式是.练习：如果将抛物线y＝－2x2＋8向右平移a个单位后，恰好过点（3，6），那么a的值为.二次函数解析式即图象变换基础巩固1、（1）一个抛物线经过（0，3）、（1，1）、（4，2）三点，求抛物线的解析式．（2）一个抛物线的顶点为（2，2），且经过（－1，－1）求抛物线的解析式．（3）一个抛物线经过（－3，0）、（1，0）、（0，－2）三点，求抛物线的解析式．（4）二次函数的图象与x轴交于A（－2，0），B（3，0）两点，且最大值为2，求二次函数的解析式．2、（1）把抛物线y＝x2－2x－3化为y＝（x－m）2＋k的形式，其中m、k为常数，则m－k＝．（2）若把二次函数y＝x2＋6x＋2化为y＝（x－h）2＋k的形式，其中m、k为常数，则h＋k＝．(3)已知抛物线抛物线y＝x2－2x－8，用配方法把y＝x2－2x－8化为y＝（x－h）2＋k的形式；抛物线的顶点坐标是，抛物线的对称轴方程是，当x时，y.随着x的增大而增大．3、（1）将抛物线y＝2x2向上平移5个单位，所得的抛物线的解析式为．（2）将二次函数y＝2x2的图象先向右平移1个单位，再向上平移3个单位后所得的抛物线的解析式为．（3）将二次函数y＝2x2的图象先向上平移2个单位，再向左平移2个单位后所得的抛物线的解析式为．（4）把二次函数y＝－2（x－3）2＋1的图象先向左平移6个单位，再向下平移2个单位，就可得到的图象.．4、将抛物线y＝3x2经过（）可得到抛物线的解析式y＝3（x－1）2＋2A. 先向左平移1个单位，再向上平移2个单位B. 先向左平移1个单位，再向下平移2个单位C. 先向右平移1个单位，再向上平移2个单位D. 先向右平移1个单位，再向下平移2个单位5、已知二次函数y＝x2－2x－1．（1）与此二次函数关于x轴对称的二次函数解析式为；（2）与此二次函数关于y轴对称的二次函数解析式为；（3）与此二次函数关于原点对称的二次函数解析式为；6、点A的坐标为（－1，0），点B的坐标为（3，0），二次函数y＝x2的图象记为抛物线l1．平移抛物线l1，使平移后的抛物线经过A、B两点，记为抛物线l2，则抛物线l2的函数表达式为．7、如图在平面直角坐标xOy中，抛物线C1顶点为A（－1，－4），且过点B（－3，0）（1）将抛物线C1向右平移2个单位得到抛物线，设C2的解析式为y＝ax2＋bx＋c，则a＝，b＝，c＝；（2）写出阴影部分的面积S＝；8、（1）已知抛物线y＝x2＋2mx－4m总经过一个定点P，并求出点P的坐标．（2）已知抛物线y＝mx2－4mx－5m总经过两个定点P，并这两个定点的坐标．综合训练9、如图，□ABCD中，AB＝4，点D的坐标为（0，8），以点C为顶点的抛物线y＝ax2＋bx＋c经过x 轴上的点A、B．（1）求A、B、C三点的坐标．（2）若抛物线向上平移后恰好经过点D，求平移后的抛物线解析式．10、如图一次函数图象与x轴y轴交于A（6，0）、B（0，23）．线段AB的垂直平分线交x轴与点C交直线AB与点D，求：（1）求这个一次函数的解析式；（2）过A，B，C三点的抛物线解析式．。

二次函数沿x轴翻折公式当事人们最兴奋的时候，大多数人都会想到翻折，无论是在纸张上还是在二次函数上，翻折操作都可以给大家带来惊喜。

有了不少发明家的努力，翻折现在可以用公式来描述，今天，让我们来看一下用来描述二次函数沿x轴翻折的精确公式。

标题探究二次函数翻折的神秘面纱：解开它的阴谋和机密！一、介绍1. 二次函数的定义二次函数是数学中两个重要数学概念的结合：函数和二次方程。

它们就像一个迷你跑车，性能强劲，动能源投入少，耗能低；它们可以帮助我们更好地了解许多自然现象，从小范围的抛物线到大范围的环境变化，它们的应用也是跨学科的。

正如许多人所熟悉的，二次函数的曲线可以描述一件美妙的作品，这就是所谓的爱情线。

就像爱情线一样，它们会带给人们美好的回忆，给人们带来更多的机会，并且更好地拥抱未来。

2. 翻折点的概念二次函数的翻折点可以说是充满神奇的，一步步实现了平面的“特技”，把一条最初水平的直线完美地翻折了一遍！看似极度普通的步骤，却有着非凡的运算原理--每一个翻折点的处理，都是一次变换的精华。

翻折点定义为一个把线段沿着一个轴翻折的点，根据位置，又可以分为上翻折点和下翻折点。

拉出一个坐标轴，用一个象征把它拉实，把它分割成左右两块，一般情况下，只要不是平行或者垂直于坐标轴的线都会到达它的两个极点，而翻折点跟这种极点不同，它不是线段的端点，而是把这条线段在x轴或y轴上翻折的承接点。

翻折点是二次函数的核心，它的重要性不是夸大的，它的位置有着重大的意义，其坐标表示一个特定的点，而一个特定的点也可以代表一个特定的函数。

只要找准了翻折点的位置，就可以利用它来把函数全部翻折完成。

二、求解翻折点1. 二次函数沿x轴翻折的公式任何一个二次函数都有可能沿着x轴翻折，但具体翻折规律如何，却让很多人陷入了迷思。

幸运的是，根据数学定理我们知道，二次函数沿x轴翻折的公式之所以使用如此的的巧妙，是因为它可以使得科学家们可以轻松地理解函数的变化过程，准确地预测函数的变化趋势，就像一颗神棍一样！下面，就来看看二次函数沿x轴翻折的公式：若二次函数y=ax²+bx+c沿着x轴翻折，则 c = -ab/4a；当a > 0时，翻折点位于x轴上横坐标为b/2a，纵坐标为ab2/4a当a < 0时，翻折点位于x轴上横坐标为b/2a，纵坐标为ab2/4a因此，在轻松理解并解决二次函数沿x轴翻折问题时，这一公式能够节省不少时间。

二次函数图像平移、旋转总归纳一、二次函数的图象的平移，先作出二次函数y=2x 2+1的图象①向上平移3个单位，所得图象的函数表达式是：y=2x 2+4；②向下平移4个单位，所得图象的函数表达式是：y=2x 2-3；③向左平移5个单位，所得图象的函数表达式是：y=2（x+5）2+1； ④向右平移6个单位，所得图象的函数表达式是：y=2（x-6）2+1． 由此可以归纳二次函数y=ax 2+c向上平移m 个单位，所得图象的函数表达式是:y=ax 2+c+m ；向下平移m 个单位，所得图象的函数表达式是:y=ax 2+c-m ；向左平移n 个单位，所得图象的函数表达式是:y=a （x+n ）2+c ； 向右平移n 个单位，所得图象的函数表达式是:y=a （x-n ）2+c ，二、二次函数的图象的翻折在一张纸上作出二次函数y=x 2-2x-3的图象，⑤沿x 轴把这张纸对折，所得图象的函数表达式是:y=x 2+2x-3． ⑥沿y 轴把这张纸对折，所得图象的函数表达式是：y=x 2+2x-3由此可以归纳二次函数y=ax 2+bx+c若沿x 轴翻折，所得图象的函数表达式是:y=-ax 2-bx-c ，若沿y 轴翻折，所得图象的函数表达式是：y=ax 2-bx+c三、二次函数的图象的旋转，将二次函数y=- x 2+x-1的图象，绕原点旋转180°，所得图象的函数表达式是y= x 2-x+1；由此可以归纳二次函数y=ax 2+bx+c 的图象绕原点旋转180°，所得图象的函数表达式是y=-ax 2-bx-c ．（备用图如下）21211、（2011•桂林）在平面直角坐标系中，将抛物线y=x 2+2x+3绕着它与y 轴的交点旋转180°，所得抛物线的解析式是（ ）A ．y=-（x+1）2+2B ．y=-（x －1）2+4C ．y=-（x －1）2+2D ．y=-（x+1）2+42、（2012浙江宁波中考）把二次函数y ＝（x －1）2＋2的图象绕原点旋转180°后得到的图象的解析式为________．3、飞机着陆后滑行的距离s （单位：m ）与滑行的时间 t （单位：s ）的函数关系式是s=60t-1.5t 2，飞机着陆后滑行的最远距离是（ ）A ．600mB ．300mC ．1200mD ．400m4、（2012•襄阳）某一型号飞机着陆后滑行的距离y （单位：m ）与滑行时间x （单位：s ）之间的函数关系式是y=60x-1.5x 2，该型号飞机着陆后滑行m 才能停下来 ．5、已知二次函数c bx ax y ++=2的图象与x 轴交于点（－2，0），(x 1，0)且1＜x 1＜2，与y·轴正半轴的交点在点(0，2）的下方，下列结论：①a ＜b ＜0；②2a+c ＞0；③4a+c< 0，④2a －b+l ＞0．其中的有正确的结论是（填写序号）__________．6、已知二次函数y ＝ax 2（a ≥1）的图像上两点A 、B 的横坐标分别是－1、2，点O 是坐标原点，如果△AOB 是直角三角形，则△OAB 的周长为 。

二次函数图像平移、旋转总归纳
一、二次函数的图象的平移，先作出二次函数y=2x2+1的图象
①向上平移3个单位，所得图象的函数表达式是：y=2x2+4；
②向下平移4个单位，所得图象的函数表达式是：y=2x2-3；
③向左平移5个单位，所得图象的函数表达式是：y=2（x+5）2+1；
④向右平移6个单位，所得图象的函数表达式是：y=2（x-6）2+1．
由此可以归纳二次函数y=ax2+c
向上平移m个单位，所得图象的函数表达式是:y=ax2+c+m；
向下平移m个单位，所得图象的函数表达式是:y=ax2+c-m；
向左平移n个单位，所得图象的函数表达式是:y=a（x+n）2+c；
向右平移n个单位，所得图象的函数表达式是:y=a（x-n）2+c，
二、二次函数的图象的翻折
在一张纸上作出二次函数y=x2-2x-3的图象，
⑤沿x轴把这张纸对折，所得图象的函数表达式是:y=x2+2x-3．
⑥沿y轴把这张纸对折，所得图象的函数表达式是：y=x2+2x-3
由此可以归纳二次函数y=ax2+bx+c
若沿x轴翻折，所得图象的函数表达式是:y=-ax2-bx-c，若沿y轴翻折，所得图象的函数表达式是：y=ax2-bx+c
三、二次函数的图象的旋转，
将二次函数y=-x2+x-1的图象，绕原点旋转180°，所得图象的函数表达式是y= x2-x+1；
由此可以归纳二次函数y=ax2+bx+c的图象绕原点旋转180°，所得图象的函数表达式是y=-ax2-bx-c．（备用图如下）。

二次函数沿一次函数翻折一次函数和二次函数都是函数中的重要概念，用于描述函数的形式和曲线的特性。

一次函数曲线为直线，被称为直线函数，可以使用一元函数表示为y=ax+b，其中a和b是常数，a不能等于0。

一次函数曲线首先是在斜率为a的直线上升段，然后平移b步，再沿b的方向下降。

一次函数曲线中若a>0，则表示函数值在x增大时函数值也随之增大，反之a<0时曲线变化为从上往下减少变化，斜率为0时曲线沿水平直线变化。

而二次函数曲线则比一次函数曲线具有更强的通用性，一般可以用二次函数来描述不同形状的曲线。

经典的二次函数形式为y=ax2+bx+c，a、b、c都是常数，其中a不能等于0。

二次函数的曲线的特点是：它的趋势先上升后下降，其最高点一定在最中间，即在横轴上有唯一的最高点，即函数在最低点出现反折两次。

可以看出，一次函数和二次函数之间是有很大区别的，不同的曲线即使表现出同样的效果也可能属于不同的函数。

如果考虑曲线的各种特性，那么一次函数与二次函数可以进行直接比较，以确定一条曲线是一次函数还是二次函数。

如果想把一次函数变为二次函数，可以沿一次函数进行翻折，使得一次函数转由深入上升变化到下降，再深入下降然后上升，同时二次函数曲线也可以根据其特点进行翻折。

翻折一次函数使之变为二次函数，首先，可以选取一次函数的坐标原点，即原点以此为支点，定义二次函数的振幅。

然后，可以用一次函数的斜率来代入二次函数的系数b，即一次函数的斜率等于二次函数的系数b，以完成翻折操作。

接下来，可以斟酌一次函数在原点两侧扩大、缩小或移动位置，以精确计算出系数a和c，从而变为完整的二次函数。

以上就是一次函数如何变为二次函数的过程，当然，将二次函数变为一次函数的方法也是一样的。

只要将它们的坐标轴、系数和振幅等参数进行一一替换就可以实现。

翻折一次函数变为二次函数的操作技巧和方法很多，需要根据具体函数形式进行综合分析，并根据其特点进行设计实现。

翻折规律1 二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1。

关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---；2。

关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4。

关于顶点对称2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5。

关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式,习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．操练:5.(2014•娄底27．（10分））如图甲，在△ABC 中，∠ACB=90°，AC=4cm,BC=3cm ．如果点P 由点B 出发沿BA 方向向点A 匀速运动,同时点Q 由点A 出发沿AC 方向向点C 匀速运动，它们的速度均为1cm/s ．连接PQ,设运动时间为t （s ）（0＜t ＜4），解答下列问题：(1）设△APQ 的面积为S ，当t 为何值时，S 取得最大值？S 的最大值是多少？(2)如图乙,连接PC ，将△PQC 沿QC 翻折,得到四边形PQP ′C ，当四边形PQP ′C 为菱形时，求t 的值；′ (3）当t 为何值时，△APQ 是等腰三角形？考点: 相似形综合题 分析：（1）过点P 作PH ⊥AC 于H,由△APH ∽△ABC ，得出=，从而求出AB ，再根据=,得出PH=3﹣t，则△AQP的面积为: AQ•PH=t（3﹣t），最后进行整理即可得出答案；(2）连接PP′交QC于E，当四边形PQP′C为菱形时,得出△APE∽△ABC，=，求出AE=﹣t+4，再根据QE=AE﹣AQ，QE=QC得出﹣t+4=﹣t+2，再求t即可；（3）由（1）知，PD=﹣t+3,与（2)同理得：QD=﹣t+4，从而求出PQ=,在△APQ中，分三种情况讨论:①当AQ=AP，即t=5﹣t，②当PQ=AQ,即=t，③当PQ=AP，即=5﹣t，再分别计算即可．解答：解:（1)如图甲，过点P作PH⊥AC于H，∵∠C=90°，∴AC⊥BC，∴PH∥BC，∴△APH∽△ABC，∴=，∵AC=4cm，BC=3cm，∴AB=5cm，∴=，∴PH=3﹣t，∴△AQP的面积为:S=×AQ×PH=×t×（3﹣t）=﹣（t﹣）2+，∴当t为秒时,S最大值为cm2．(2)如图乙，连接PP′,PP′交QC于E,当四边形PQP′C为菱形时，PE垂直平分QC，即PE⊥AC，QE=EC，∴△APE∽△ABC，∴=,∴AE===﹣t+4QE=AE﹣AQ═﹣t+4﹣t=﹣t+4，QE=QC=（4﹣t）=﹣t+2，∴﹣t+4=﹣t+2，解得:t=,∵0＜＜4，∴当四边形PQP′C为菱形时，t的值是s；（3）由（1）知，PD=﹣t+3，与(2）同理得：QD=AD﹣AQ=﹣t+4∴PQ===，在△APQ中，①当AQ=AP，即t=5﹣t时，解得：t1=；②当PQ=AQ,即=t时，解得：t2=,t3=5；③当PQ=AP，即=5﹣t时，解得：t4=0,t5=;∵0＜t＜4，∴t3=5，t4=0不合题意，舍去，∴当t为s或s或s时，△APQ是等腰三角形．点评:此题主要考查了相似形综合，用到的知识点是相似三角形的判定与性质、勾股定理、三角形的面积公式以及二次函数的最值问题，关键是根据题意做出辅助线，利用数形结合思想进行解答．17. ( 2014年河南） (23. 11分）如图,抛物线y=－x2+bx+c与x轴交于A（－1，0）,B(5，0）两点，直线y=－34x+3与y轴交于点C，,与x轴交于点D。

二次函数12345定理二次函数是数学中的一个重要分支，其成为学习数学的一大难题之一。

而在二次函数学习的过程中，较为常见的概念之一是“二次函数12345定理”。

本文将通过多方面的解析，给出较为详细的解释，帮助读者更好的理解和掌握这一重要的概念。

一、什么是二次函数12345定理？“二次函数12345定理”是指二次函数的5个常用变数，即：平移(x-k)倍数;垂直翻折±a;水平翻折x=k;(x,y)→(x+a,y+k);垂直平移。

也就是说，对于一般二次函数y=ax2+bx+c，通过对其进行常见的平移、翻折、拉伸等操作，可以得到一系列不同的二次函数。

而这些常用操作被统称为“二次函数12345定理”。

二、“二次函数12345定理”的详细解释1. 平移平移指的是将二次函数图像上的点整体沿横轴或纵轴移动一段距离。

平移的方向和距离都可以自由指定。

可以写成：(x-k)和y-k。

其中，k为平移的大小，正数表示向右移，负数表示向左移；y和x的平移方向则相反。

2. 垂直翻折±a垂直翻折指将二次函数图像上的点整体沿x轴上下翻折。

可以写成：-ax2或ax2。

当a为正数时，翻折后的函数面向上方，当a为负数时，翻折后的函数面向下方。

3. 水平翻折x=k水平翻折指将二次函数图像上的点整体沿y=k翻折。

可以写成：a(x-k)2。

其中，k即为翻折线的横坐标。

4. (x,y)→(x+a,y+k)(x,y)→(x+a,y+k)指将二次函数图像上的点整体沿x 轴或y轴移动一段距离。

其中，a和k分别为x轴和y轴的平移距离，正数表示向右或上移，负数表示向左或下移。

5. 垂直平移垂直平移指将二次函数图像上的点整体沿y轴上下移动一段距离。

可以写成：ax2+b(x-k)+c±k。

其中，k为平移的大小，正数表示向上移，负数表示向下移。

三、如何运用“二次函数12345定理”？掌握“二次函数12345定理”，可以方便地确定二次函数的图像，更好地理解函数的性质，并且更快速地解决与二次函数相关的题目。