2019-2020学年湖南省炎德英才杯2019级高一下学期基础学科知识竞赛数学试卷及答案
- 格式:doc
- 大小:1.42 MB
- 文档页数:10


湖南省炎德英才杯2019-2020学年高一物理下学期基础学科知识竞赛试题时量:90分钟满分:100分一、单项选择题:本题共8小题,每小题3分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.牛顿时代的科学家们围绕万有引力的研究,经历了大量曲折顽强而又闪烁智慧的科学实践。
在万有引力定律的发现历程中,下列叙述符合史实的是A.伽利略研究了第谷的行星观测记录,提出了行星运动定律B卡文迪许将行星与太阳、地球与月球、地球与地面物体之间的引力推广到宇宙中的一切物体,得出了万有引力定律C.哈雷在实验室中准确地得出了引力常量G的数值,使得万有引力定律有了现实意义D.牛顿通过月地检验,验证了万有引力定律2.甲,乙两物体同时以相同的速度经过某个位置时开始计时,从t=0时刻开始两物体沿同一直线做减速运动,最终又都停止在另一相同的位置,整个过程甲、乙运动的v-t图象如图所示,则A.整个过程中甲的平均速度大于乙的平均速度B.从t=0时刻到下一次速度相等的过程中,乙的平均速度要大于甲的平均速度C.在运动过程中甲的加速度一直小于乙的加速度D.在运动过程中甲,乙两物体的加速度不可能相同3.如图所示,重物M沿竖直杆下滑,并通过一根不可伸长的细绳带动小车沿水平面向右运动。
若当滑轮右侧的绳与竖直方向成β=60°角,且重物下滑的速率为v=2m/s时,滑轮左侧的绳与水平方向成α=45°角,则小车的速度为A.23m/sB.3m/sC.22m/sD.2m/s4.在一斜面頂端,将质量相等的甲、乙两个小球分别以2v 和v 的速度沿同一方向水平抛出,两球都落在该斜面上。
则下列说法正确的是A 乙球落到斜面上时速度方向与水平方向的夹角要比甲球的小B.从抛出到落到斜面上重力对甲,乙两球做功之比为1:2C.落到斜面上时甲,乙两球重力的瞬时功率之比为1:2D.两球从抛出到落到斜面上运动的时间相同5.2019年春节期间,中国科幻电影里程碑作品《流浪地球》热播,影片中为了让地球逃离太阳系,人们在地球上建造特大功率发动机,使地球完成一系列变轨操作,其逃离过程可设想成如图所示,地球在椭圆轨道I 上运行到远日点B 变轨,进入圆形轨道II 。

高一基础学科知识竞赛英语时量: 120分钟满分: 150分得分第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1.How does the man usually goto school?A.By bus.B.By taxi.C.By bike.2.Which book does the woman like most?A.Great Expectations.B.David Copperfield.C.Oliver Twist.3.Why does the man get up late?A.He doesn't have to work today.B.He forgot to set an alarm clock.C.He stayed up late last night.4.When is the woman likely to buy a computer?A.In September.B.In July.C.In June.5.What are the speakers mainly talking about?A.An interview.B.A job offer.C.A company.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。



2020年“炎德英才杯”高二基础学科知识竞赛数学时量:120分钟 满分:150分一、单项选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知命题p :∀x>0,ln(x +1)>0,则命题p 的否定是A.∀x>0,ln(x +1)≤0B.∀x ≤0,ln(x +1)>>0C.∃x 0>0,ln(x 0+1)>0D.∃x 0>0,ln(x 0+1)≤02.已知集合A ={x|-1<x<2},B ={t ∈Z|t =2x +1,x ∈A},则A ∩B =A.{-1,0,1} B{-1,0} C{0,1} D.{0}3.已知正项等比数列{a n }的公比为q ,若a 2a 6=4a 52,则公比q = A.12 B.22 C.2 D.24.已知a ,b 均为单位向量,它们的夹角为60°,c =λa +µb ,若a ⊥c ,则下列结论正确的是 Aλ-μ=0 B.λ+μ=0 C.2λ-μ=0 D.2+μ=05.(2x 2+1x)5的展开式中,x 4的系数是 A160 B.80 C.50 D.106.已知cos(α-4π)sin(34π-α)=33,α∈(3,24ππ),则sin2α= A.231- B.231- C.31- D.31+ 7.唐朝著名的凤鸟花卉纹浮雕银杯如图1所示,它的盛酒部分可以近似地看作是半球与圆柱的组合体(如图2).当这种酒杯内壁表面积(假设内壁表面光滑,表面积为S 平方厘米,半球的半径为R 厘米)固定时,若要使得酒杯的容积不大于半球体积的2倍,则R 的取值范围为A.(0 ) ) 8.巳知实数a ,b 满足ab>0,则2a a a b a b-++的最大值为A.2B.2C.3-D.3+二、多项选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合要求全部选对的得5分,部分选对的得3分,有选错的得0分。



2020年“炎德英才杯”高二基础学科知识竞赛数学时量:120分钟 满分:150分得分:_____________一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知命题p :0x ∀>,()ln 10x +>,则命题p 的否定是( ) A.0x ∀>,()ln 10x +≤ B.0x ∀≤,()ln 10x +> C.00x ∃>,()0ln 10x +>D.00x ∃>,()0ln 10x +≤2.已知集合{}|12A x x =-<<,{}|21,B t t x x A =∈=+∈Z ,则A B =( )A.{}1,0,1-B.{}1,0-C.{}0,1D.{}03.已知正项等比数列{}n a 的公比为q ,若22654a a a =,则公比q =( )A.12B.2D.24.已知a ,b 均为单位向量,它们的夹角为60°,c a b λμ=+.若a c ⊥,则下列结论正确的是( ) A.0λμ-=B.0λμ+=C.20λμ-=D.20λμ+=5.5212x x ⎛⎫+ ⎪⎝⎭的展开式中,4x 的系数是( )A.160B.80C.50D.106.已知3cos sin 44ππαα⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭,3,24ππα⎛⎫∈ ⎪⎝⎭,则sin 2α=( )1- 1- 7.唐朝著名的凤鸟花卉纹浮雕银杯如图1所示,它的盛酒部分可以近似地看作是半球与圆柱的组合体(如图2).当这种酒杯内壁表面积(假设内壁表面光滑,表面积为S 平方厘米,半球的半径为R 厘米)固定时,若要使得酒杯的容积不大于半球体积的2倍,则R 的取值范围为( )A.⎛ ⎝B.⎫+∞⎪⎪⎭C.D. 8.已知实数a ,b 满足0ab >,则2a a a b a b-++的最大值为( )A.2B.2C.3-D.3+二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.在平面直角坐标系xOy 中,双曲线A 的焦点F 位于x 轴上,且双曲线A 与双曲线B :2213x y -=有相同渐近线,则下列结论正确的是( ) A.双曲线A 与双曲线B的离心率相等 B.双曲线A 与双曲线B 的焦距相等C.若双曲线A 的焦点F 到渐近线距离为2.则双曲线A 的标准方程为22162x y -= D.若双曲线A 的焦点F 到渐近线距离为2.则双曲线A 的标准方程为221124x y -= 10.2019年国际数学奥林匹克竞赛(IMO )中国队王者归来,6名队员全部摘金,总成绩荣获世界第一,数学奥林匹克协会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往机场接参赛选手.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为1P ,2P ,则下列结论正确的是( ) A.12P P <B.12P P =C.1223P P =D.1256P P +=11.如图所示,已知棱长为1的正方体1111ABCD A B C D -中,E ,F ,M 分别是线段AB 、AD 、1AA 的中点,点P 、Q 分别在线段11A B 、11A D 上,且11A P AQ x ==(01x <<).设平面MEF 平面MPQ l =,则下列结论正确的是( )A.//l 平面ABCDB.l AC ⊥C.直线l 与平面11BCC B 不垂直D.当x 变化时,l 不是定直线12.已知函数()()sin f x x ωϕ=+(0ω>)满足()()00112f x f x =+=-,且()f x 在()00,1x x +上有最小值,无最大值.则下述四个结论正确的是( ) A.0112f x ⎛⎫+=- ⎪⎝⎭B.若00x =,则()sin 26f x x ππ⎛⎫=- ⎪⎝⎭C.()f x 的最小正周期为3D.()f x 在()0,2019上的零点个数最少为1345个 三、填空题:本题共4小题,每小题5分,共20分. 13.已知i 是虚数单位,复数i z a =+(a ∈R ),且满足13i1z z -=+,则z =_______________. 14.已知函数()11x f x x +=+,则()()222f x x f x -<-的解集是_______________. 15.已知抛物线Γ:22y px =(0p >)的焦点为F ,准线为直线l ,点A 与F 在准线l 的两侧,且AF l ⊥,2AF p =,03,2p B y ⎛⎫⎪⎝⎭是抛物线Γ上的一点,BC 垂直l 于点C ,AB 分别交l ,CF 于点D ,E .则BC =_______________;若EF DF λ=,则λ的值为_______________.16.已知函数()32113f x x ax ax =-++(1a ≤)在不同的两点()()111,P t f t ,()()222,P t f t 处的切线的斜率相等,若不等式()120f t t m ++≥(m ∈R )恒成立,则实数m 的取值范围是_______________. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)在①22430a b b ++=,②44a b =,③327S =-这三个条件中任选一个补充在下面问题中,并解答问题.设等差数列{}n a 的前n 项和为n S ,数列{}n b 的前n 项和为n T ,___________,51a b =,431n n T b =-(*n ∈N ),是否存在实数λ,对任意*n ∈N 都有n S λ≤?若存在,求实数λ的取值范围;若不存在,请说明理由.(注:如果选择多个条件分别解答,按第一个解答计分) 18.(本小题满分12分)三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin 2Ba b A =. (1)求B ;(2)若ABC △为锐角三角形,且1c =,求ABC △面积的取值范围. 19.(本小题满分12分)已知四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,且60ABC ∠=︒,PA ⊥平面ABCD ,E ,M分别是BC ,PD 上的中点,直线EM 与平面PAD ,点F 在PC 上移动. (1)证明:无论点F 在PC 上如何移动,平面AEF ⊥平面PAD ; (2)若点F 为PC 的中点,求二面角C AF E --的余弦值. 20.(本小题满分12分)过椭圆C :22221x y a b+=(0a b >>)内一点()0,1A 的动直线l '与椭圆相交,当l '平行于x 轴和垂直于x 轴时,l '被椭圆C 所截得的线段长均为. (1)求椭圆C 的标准方程;(2)过点)F作直线l 交椭圆C 于点M ,N ,求三角形OMN 面积的最大值.21.(本小题满分12分)华为手机的“麒麟970”芯片在华为处理器排行榜中最高主频2.4GHz ,同时它的线程结构也做了很大的改善,整个性能及效率至少提升了50%,科研人员曾就是否需采用西门子制程这一工艺标准进行了反复比较,在一次实验中,工作人员对生产出的50片芯片进行研究,结果发现使用了该工艺的30片芯片有28片线程结构有很大的改善,没有使用该工艺的20片芯片中有12片线程结构有很大的改善.(1)用列联表判断:这次实验是否有99.5%的把握认为“麒麟970”芯片的线程结构有很大的改善与使用西门子制程这一工艺标准有关?(2)在“麒麟970”芯片的线程结构有很大的改善后,接下来的生产制作还需对芯片的晶圆依次进行金属溅镀,涂布光阻,蚀刻技术,光阻去除这四个环节的精密操作,进而得到多晶的晶圆,生产出来的多晶的晶圆经过严格的质检,确定合格后才能进入下一个流程.如果生产出来的多晶的晶圆在质检中不合格,那么必须依次对前四个环节进行技术检测并对所有的出错环节进行修复才能成为合格品.在实验的初期,由于技术的不成熟,生产制作的多晶的晶圆很难达到理想状态,研究人员根据以往的数据与经验得知在实验生产多晶的晶圆的过程中,前三个环节每个环节生产正常的概率为23,每个环节出错需要修复的费用均为200元,第四环节生产正常的概率为34,此环节出错需要修复的费用为100元,问:一次试验生产出来的多晶的晶圆要成为合格品大约还需要消耗多少元费用?(假设质检与检测过程不产生费用)参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.参考数据:22.(本小题满分12分)已知函数()12e x ax af x x --+=,()()221ln g x a x ax x=---,其中0a ≥. (1)当1a =时,求曲线()y f x =在点()()1,1P f 处的切线方程;(2)设函数()()()F x f x g x =+,若2x =是()F x 的唯一极值点,求a 取值的集合.2020年“炎德英才杯”高二基础学科知识竞赛数学参考答案一、单项选择题:本题共8小题,每小题5分,共40分.1.D 【解析】由含有量词的命题的否定的定义可知D 选项正确,故选D.2.C 【解析】由已知{}|12A x x =-<<,则()211,5t x =+∈-,所以{}0,1,2,3,4B =,所以{}0,1AB =,故选C.3.A 【解析】由2226454a a a a==,得2252414a q a ==,又0q >,所以12q =,故选A.4.D 【解析】因为a c ⊥,所以()0a c a a b λμ⋅=⋅+=,可得02μλ+=,即20λμ+=.故选D.5.B 【解析】依题5212x x ⎛⎫+ ⎪⎝⎭的展开式的通项为:()5251031551C 2C 2rr r r r rr T x xx ---+⎛⎫== ⎪⎝⎭,当1034r -=时,2r =,此时52355C 2C 280rr-==,所以5212x x ⎛⎫+ ⎪⎝⎭的展开式中,4x 的系数是80.故选B.6.A 【解析】因为3sin sin cos cos 42444πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-=-⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,又3cos sin 443ππαα⎛⎫⎛⎫--=⎪ ⎪⎝⎭⎝⎭,所以21cos 21sin 22cos 422παπαα⎛⎫+- ⎪+⎛⎫⎝⎭-=== ⎪⎝⎭,则sin 21α=.故选A. 7.D 【解析】设圆柱的高为h ,则222S R Rh ππ=+,则22SRh R ππ=-, 所以酒杯的容积323233224332323S S V R R h R R R R R R ππππππ⎛⎫=+=+-=-+≤ ⎪⎝⎭, 又0h >,所以202S R π->,所以22523S R R ππ<R ≤< D. 8.C 【解析】由题意,()()()()222221222323a ab a ab a a ab a b a b a b a b a b a ab b b a+-+-===≤++++++++3=-a =时“=”成立,故选C.二、多项选择题:本题共4小题,每小题5分,共20分. 9.AD【解析】由题设双曲线A 与双曲线B的离心率3e ==,所以选项A 正确; 由双曲线A 与双曲线B :2213x y -=有相同渐近线.则双曲线A 的标准方程可设为号号-y =入,因为双曲线A的焦点在z 轴上,故入>0,若焦点到渐近线的距离为2,则入=4,所以双曲线A 的标准方程为223x y λ-=,且双曲线A 的焦距为8,而双曲线B 的焦距为4,所以选项BC 错误,选项D 正确.故选AD. 10.CD 【解析】三辆车的出车顺序可能为:123、132、213、231、312、321, 方案一坐到“3号”车可能:132、213、231,所以136P =; 方案二坐到“3号”车可能:312、321,所以226P =; 所以1223P P =,1256P P +=,故选CD. 11.ABC 【解析】连接BD ,11B D ,∵11A P AQ x ==,∴11//////PQB D BD EF ,易证//PQ 平面MEF ,又平面MEF平面MPQ l =,∴//PQ l ,//l EF ,∴//l 平面ABCD ,故A 成立;又EF AC ⊥,∴l AC ⊥,故B 成立;∵////l EF BD ,∴易知直线l 与平面11BCC B 不垂直,故C 成立;当x 变化时,l 是过点M 且与直线EF 平行的定直线,故D 不成立.故选ABC. 12.ACD 【解析】()00,1x x +的区间中点为012x +,根据正弦曲线的对称性知0112f x ⎛⎫+=- ⎪⎝⎭,A 正确;若00x =,()sin 26f x x ππ⎛⎫=-⎪⎝⎭,则113f ⎛⎫= ⎪⎝⎭为()0,1上的最大值,不满足条件,故B 错误;0526x k πωϕπ+=-,()0126x k πωϕπ++=-,k ∈Z ,两式相减得23πω=,即函数的周期23T πω==,故C 正确;区间()0,2019的长度恰好为673个周期,当()00f =时,即k ϕπ=时,()f x 在开区间()0,2019上零点个数至少为673211345⨯-=,故D正确.故选ACD.三、填空题:本题共4小题,每小题5分,共20分.()()222i i121i13iz z a a a a a+=+++=-+++=-,所以211,213,a aa⎧-+=⎨+=-⎩解得2a=-,所以2iz=-+=14.02x<<【解析】由已知()1,0,21,0,1xf xxx≥⎧⎪=⎨--<⎪-⎩所以()f x在(),0-∞上单调递增,在[)0,+∞上为常数函数,则2222,20,x x xx x⎧-<-⎨-<⎩解得02x<<.15.2p【解析】由题设3,2pB y⎛⎫⎪⎝⎭及抛物线的定义得3222p pBC BF p==+=;由题设//BC AF,又2BC AF p==,所以四边形AFBC为平行四边形,∴EF EC=,2FC p=,∴FE p=,∵12AD AMBD BC==,∴13AD AB=,AB==,∴AD p=,又DM为AF的中垂线,所以DF AD p==,所以EFDF=故λ=. 16.[)1,-+∞【解析】由题得()22f x x ax a'=-+(1a≤),由已知得1t,2t为22x ax a c-+=(c为常数)的两个不等实根,所以122t t a+=,∵()12f t t m++≥恒成立,∴()2m f a-≤(1a≤)恒成立.令()()3242213g a f a a a==-++(1a≤),则()()24441g a a a a a '=-+=--,当(),0a ∈-∞,()0g a '<,当()0,1a ∈,()0g a '>; ∴()g a 在(),0-∞上单调递减,在()0,1上单调递增.∴()()min 01g a g ==, ∴1m -≤,∴1m ≥-.故实数m 的取值范围是[)1,-+∞. 四、解答题:本题共6小题,共70分. 17.【解析】设等差数列{}n a 的公差为d ,当1n =时,11431T b =-,得11b =-,从而51a =-,当2n ≥时,()()111444313133n n n n n n n b T T b b b b ---=-=---=-,得13n n b b -=-, 所以数列{}n b 是首项为1-,公比为3-的等比数列,所以()13n n b -=--, ································ 3分由对任意*n ∈N ,都有n S λ≤,可知等差数列{}n a 的前n 项和n S 存在最小值,假设n k =时,n S 取最小值,所以111,0,0,k k kk k k S S a S S a -++≥≤⎧⎧⇔⎨⎨≤≥⎩⎩ ···················································································· 5分 (1)若补充条件是①22430a b b ++=, 因为23b =,427b =,从而()2241103a b b =-+=-,由523a a d =+得3d =, 所以()()()12121032316n a a n d a n d n n =+-=+-=-+-=-, ······································· 7分 由等差数列{}n a 的前n 项和n S 存在最小值,又*k ∈N ,所以5k =,所以535S λ≤=-,故实数λ的取值范围为(],35-∞-. ······················ 10分(2)若补充条件是②44a b =,由427b =,即427a =,又511a b ==-, 所以5412728d a a =-=--=-;所以()()()1515128528139n a a n d a n d n n =+-=+-=---=-+, ·································· 7分由等差数列{}n a 的前n 项和n S 存在最小值,则()281390,2811390,k k -+≤⎧⎨-++≥⎩得1392811128k k ⎧≥⎪⎪⎨⎪≤⎪⎩,所以k ∈∅,所以不存在k ,使得n S 取最小值,故实数λ不存在. ····························································· 10分(3)若补充条件是③327S =-,由31232327S a a a a =++==-得,29a =-,又51213a b a d ==-=+, 所以52833a a d -==, 所以()()()1288431292333n a a n d a n d n n =+-=+-=-+-=-, ······································· 7分 由等差数列{}n a 的前n 项和n S 存在最小值,则()8430,3384310,33k k ⎧-≤⎪⎪⎨⎪+-≥⎪⎩得354388k ≤≤,又*k ∈N ,所以5k =,所以存在5k =,使得n S 取最小值, 所以5953S λ≤=-,故实数λ的取值范围为95,3⎛⎤-∞- ⎥⎝⎦. ····················································· 10分18.【解析】(1)根据题意cossin 2B a b A =,由正弦定理得sin cos sin sin 2BA B A =. 因为0A π<<,所以sin 0A >,又222B A C π+=-,得sin sin 2A CB +=. ····························· 2分 因为0B π<<,022AC π+<<,所以2A C B +=或者2A CB π++=, ································ 3分 而根据题意A BC π++=,故2A CB π++=不成立, 所以2A C B +=,又因为A B C π++=,代入得3B π=,所以3B π=. ··································· 5分 (2)因为ABC △是锐角三角形,由(1)知3B π=,A B C π++=得到23A C π+=, 故0,220,32C C πππ⎧<<⎪⎪⎨⎪<-<⎪⎩解得62C ππ<<. ··············································································· 7分又应用正弦定理sin sin a cA C=,1c =, 由三角形面积公式有:222sin 111sin 3sin sin sin 222sin sin ABCC a A S ac B c B c B c C C π⎛⎫- ⎪⎝⎭=⋅=⋅=⋅=△22sincos cos sin 2123133sin cossin 3tan 38tan C CC C C ππππ-⎛⎫==⋅-= ⎪⎝⎭. ·············· 10分 又因为62C ππ<<,tan C >318tan C <<ABC S <<△.故ABC S △的取值范围是82⎛ ⎝⎭. ····················································· 12分 19.【解析】(1)因为底面ABCD 为菱形,60ABC ∠=︒,所以ABC △是正三角形,又E 是BC 的中点,所以AE BC ⊥,又//AD BC ,所以AE AD ⊥. ······································· 2分 因为PA ⊥平面ABCD ,AE ⊂平面ABCD ,所以PA AE ⊥, 又PAAD A =,所以AE ⊥平面PAD ,又AE ⊂平面AEF ,所以平面AEF ⊥平面PAD .(2)由(1)得,AE ,AD ,AP 两两垂直,以AE ,AD ,AP 所在直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,因为AEF ⊥平面PAD .,所以AME ∠就是直线EM 与平面PAD 所成的角, 在Rt AME △中,由sin AME ∠=tan AE AME AM ∠==,由已知2AB =,则AE =AM =所以2PD AM ==,即(2222AP =+,从而2AP =, ·············································································································· 7分 则()0,0,0A,)1,0B-,)C,()0,2,0D ,()0,0,2P,)E,1,122F ⎛⎫⎪ ⎪⎝⎭,所以)AE =,1,12AF ⎫=⎪⎪⎝⎭, ········································································ 8分设(),,n x y z =是平面AEF 的一个法向量,则30,310.2n AE n AF x y z ⎧⋅==⎪⎨⋅=++=⎪⎩ 取1z =,得()0,2,1n =-.又BD ⊥平面ACF ,∴()BD =是平面ACF 的一个法向量, ·································· 10分所以()02310cos ,5n BD n BD n BD ⨯+-⨯+⨯⋅===-, 由图可知C AF E --为锐二面角,所以二面角C AF E --的余弦值为5. ·························· 12分 20.【解析】(1)由已知得b = ·················································································· 2分点)在椭圆上,所以22211a b+=.解得2a =, ······························································ 4分 所以椭圆C 的标准方程为22142x y +=. ··············································································· 5分(2)设()11,M x y ,()22,N xy ,由(1)可知)F 为C 的右焦点,且直线l 的斜率不为0,设直线l 的方程为x my =+由2224,x my x y ⎧=⎪⎨+=⎪⎩得()22220m y ++-=. 所以121222,2y y y y m ⎧+=⎪⎪⎨⎪=-⎪+⎩································································································7分 所以12y y -=== ······························ 9分所以三角形OMN 的面积121122S OF y y=-==≤=当且仅当0m=时等号成立,故三角形OMN.·········································12分21.【解析】(1)由题意列联表为:··································································································································2分故()2250288212257.879302040103K⨯-⨯==>⨯⨯⨯, ······································································4分故有99.5%的把握认为“麒麟970”芯片的线性结构有很大的改善与使用西门子制程这一工艺技术有关. ··································································································································5分(2)设iA表示检测到第i个环节有问题(1i=,2,3,4),X表示成为一个合格的多晶的晶圆需消耗的费用,则X的可能取值为:0,100,200,300,400,500,600,700, ·······································6分0X=表明四个环节均正常()3123423240()34108P X P A A A A⎛⎫===⋅=⎪⎝⎭,100X=表明第四环节有问题()()3123421810034108P X P A A A A⎛⎫===⋅=⎪⎝⎭,200X=表明前三环节有一环节有问题()21312336200C334108P X⎛⎫⎛⎫==⋅⋅=⎪ ⎪⎝⎭⎝⎭,300X=表明前三环节有一环节及第四环节有问题()21312112300C334108P X⎛⎫⎛⎫==⋅⋅=⎪ ⎪⎝⎭⎝⎭,400X=表明前三环节有两环节有问题()22312318400C334108P X⎛⎫⎛⎫==⋅⋅=⎪ ⎪⎝⎭⎝⎭,500X=表明前三环节有两环节及第四环节有问题()2231216500C334108P X⎛⎫⎛⎫==⋅⋅=⎪ ⎪⎝⎭⎝⎭,600X=表明前三环节有问题()()3123413360034108P X P A A A A⎛⎫===⋅=⎪⎝⎭700X =表明四个环节均有问题()()3123411170034108P X P A A A A ⎛⎫===⋅=⎪⎝⎭. ······················ 10分 费用X 分布列为:故0241008200363001240018500660037001225108EX ⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==(元),故大约需要耗费225元. ································································································· 12分22.【解析】(1)当1a =时,()12e 1x xf x x --+=,则()11f =.又()()()()()121143e 12e 12e 1x x x x x x xf x x x ------+-+'==,得() 12f '=-, ························· 3分所以()f x 在点()()1,1P f 处的切线方程为()121y x -=--,即230x y +-=. ··········································································································· 4分(2)由题意可得:()()122e 21ln x ax aF x a x ax x x--+=---+, ()()()()()()()1122332e 2e 21x x x a x ax x a x ax F x x x x ---+---+-+'=-+=, 由于2x =是()F x 的唯一极值点,则有以下两种情形: 情形一:12e 0x ax x a ---+≥对()0,x ∀∈+∞恒成立.情形二:12e0x ax x a ---+≤对()0,x ∀∈+∞恒成立. ·························································· 6分设()12e x h x ax x a -=--+,()0,x ∈+∞,则()10h =,()1e 21x h a x x -'=--, ①当0a =时,()1e 1x h x -'=-,可知1x =时,函数()h x 取得极小值即最小值,所以()()10h x h ≥=.满足题意. ························································································ 7分 ②当0a >时,设()1e 21x p x ax -=--,x ∈R ,()1e 2x p x a -'=-,可得()p x 在(),1ln 2a -∞+上单调递减;在()1ln 2,a ++∞上单调递增. ··································· 8分(ⅰ)当12a >时,1ln 21a +>,由()()p x h x ='在()0,1ln 2a +上单调递减,可得()()00h x h '<'<, 所以()h x 在()0,1ln 2a +上单调递减, 所以()()1101ln 22h h h a ⎛⎫>=>+⎪⎝⎭,与题意矛盾,舍去. ··················································· 10分 (ⅱ)当102a <≤时,1ln 21a +≤,由()()p x h x ='的单调性及()00h '<,()10h '<, 可知()0,1x ∈时,都有()0h x '<.又()()p x h x ='在()1,3上单调递增, 又()221e 61e 402h x '≥-⨯-=->,则存在()11,3x ∈,使得()10h x '=. 当()10,x x ∈时,()0h x '<,此时()h x 单调递减, 所以()()11102h h h x ⎛⎫>=>⎪⎝⎭,与题意矛盾,舍去. 综上可得:0a =. ········································································································ 12分。

湖南省炎德英才杯2019-2020学年高二物理下学期基础学科知识竞赛试题时量:90分钟满分:100分一、单项选择题:本题共8小题,每小题3分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.一沿直线运动的物体的a-x图象如图所示,则其v2-x图象可能是2.如图所示,轻杆的一端固定一光滑球体,杆以另一端O为自由转动轴,而球又搁置在光滑斜面上,若杆与竖直墙面的夹角为β,斜面倾角为α,开始时β<α,β+a<90°,则为使斜面能在光滑水平面上缓慢向右运动,在球体离开斜面之前,作用于斜面上的水平外力F的大小、轻杆受力T和地面对斜面的支持力N的大小变化情况是A.F逐渐增大,T逐渐减小,N逐渐减小B.F逐渐减小,T逐渐减小,N逐渐增大C.F逐渐增大,T先减小后增大,N逐渐增大D.F逐渐减小,T先减小后增大,N逐渐减小3.如图所示,是竖直平面内的直角坐标系,P、Q分别是y轴和工轴上的一点,这两点到坐标原点的距离均为L从P点沿I轴正向抛出一个小球,小球只在重力作用下运动,恰好经过Q 点,现改变抛出点的位置(仍从第一象限抛出),保持抛出速度的大小和方向不变,要使小球仍能经过Q点,则新的抛出点坐标(x,y)满足的函数关系式为A.y=()2L xL-B.y=()23L x2L-C.y=()2L x2L-D.y=()22L xL-4.如图(a)所示,用卡车运输每根质量为m的匀质圆柱形水泥管,底层水泥管固定在车厢内,上层水泥管堆放在底层上,如图(b)所示。
已知水泥管之间的动摩擦因数为μ。
重力加速度为g,下列说法正确的是A.当卡车沿平直公路匀速行驶时,水泥管A、B之间的弹力大小为12mgB.当卡车沿平直公路匀速行驶时,水泥管A、C之间的弹力大小为33mgC.当卡车刹车时,水泥管A、B 3µmgD.当卡车刹车时,水泥管A.C之间的摩擦力大小为µmg5.将一段裸铜导线弯成如图甲所示形状的线框,将它置于一节5号干电池的正极上(线框上端的弯折位置与正极良好接触),一块圆柱形强磁铁吸附在电池的负极,使铜导线框下面的两端P、Q与磁铁表面保持良好接触,放手后线框就会发生转动,从而制成了一个“简易电动机”,如图乙所示。
2019-2020学年湖南省炎德英才杯高一下学期基础学知识竞赛数学试题一、单选题 1.已知集合{}|22xA x =>,{}2|,RB y y x x ==∈,则()R A B =( )A .[0,1)B .(0,2)C .(,1]-∞D .[0,1]【答案】D【解析】根据指数函数单调性,求出{|1}A x x =>,得出R{|1}A x x =,求出集合B ,根据交集的计算即可得出答案. 【详解】解:由题可知,{}|22{|1}xA x x x =>=>,R {|1}A x x ∴=,{}2|,{|0}B y y x x y y ==∈=R ,所以()R{|01}B x A x ⋂=.故选:D. 【点睛】本题考查集合的交集和补集运算,属于基础题.2.设()f x 是定义域为R 的偶函数,且()()31f x f x +=-,若当[]2,0x ∈-时,()2x f x -=,记21log 4a f ⎛⎫= ⎪⎝⎭,b f=,()23c f =,则a ,b ,c 的大小关系为( ) A .a b c >> B .c b a >>C .c a b >>D .a c b >>【答案】A【解析】根据()()31f x f x +=-可得函数()f x 是周期为4的周期函数,根据()f x 是定义域为R 的偶函数,可得()f x 为(0,2]上的增函数,再根据周期性和单调性可比较大小. 【详解】∵()()31f x f x +=-,∴()()4f x f x +=,即函数()f x 是周期为4的周期函数, 当[]2,0x ∈-时,()2xf x -=,则函数()f x 为减函数,即当(]0,2x ∈时,()f x 为增函数, 21log 24=-,则()()21log 224a f f f ⎛⎫==-= ⎪⎝⎭, ()()()()239811c f f f f ===+=,∵132<<,且当(]0,2x ∈时,()f x 为增函数,∴()()()132f f f <<,∴a b c >>,故选:A . 【点睛】本题考查了利用函数的奇偶性、周期性和单调性比较大小,属于基础题. 3.在ABC 中,D 是边AC 上的点,且AD AB =,3BD AB =,2BC BD =,则sin C 的值为( )A .12B .14C .18D .112【答案】B【解析】设AB x =,则AD x =,3BD x =,23BC x =,过点A 作AE BD ⊥,利用正弦定理sin sin BC ABBAC C=∠,即可得答案;【详解】在ABC 中,D 是边AC 上的点,且AD AB =,3BD AB =,2BC BD =,设AB x =,则AD x =,3BD x =,23BC x =,如图所示,过点A 作AE BD ⊥,所以32BE x =,3BAE π∠=,所以23BAC π∠=, 在ABC 中,利用正弦定理sin sin BC ABBAC C=∠,所以23sin 32x xC =,整理得1sin 4C =, 故选:B. 【点睛】本题考查正弦定理在解三角形中的运用,考查运算求解能力.4.如图,圆O 是边长为23的等边三角形ABC 的内切圆,其与BC 边相切于点D ,点M 为圆上任意一点,BM xBA yBD =+(,)x y ∈R ,则2x y +的最大值为( )A 2B 3C .2D .2【答案】C【解析】建立坐标系,写出相应的点坐标,得到2x y +的表达式,进而得到最大值. 【详解】以D 点为原点,BC 所在直线为x 轴,AD 所在直线为y 轴,建立坐标系,设内切圆的半径为1,以(0,1)为圆心,1为半径的圆; 根据三角形面积公式得到011sin 6022l r S AB AC ⨯⨯==⨯⨯⨯周长, 可得到内切圆的半径为1; 可得到点的坐标为:())()()()3,0,3,0,0,3,0,0,cos ,1sin B CA D M θθ-+()cos 3,1sin ,BM θθ=+()()3,3,3,0BD BA == 故得到 ())cos 3,1sin 33,3x BM x θθ=++=故得到cos 333,sin 31x x θθ=+=-1sin 3sin 2333x y θθ+⎧=⎪⎪⇒⎨⎪=+⎪⎩,()sin 4242sin 2.33333x y θθϕ+=++=++≤ 故最大值为:2. 故答案为C. 【点睛】这个题目考查了向量标化的应用,以及参数方程的应用,以向量为载体求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法.5.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +14 )A .12πB .32πC .8πD .24π【答案】A【解析】将侧面ABC 和ACD △沿AC 边展开成平面图形为菱形ABCD ,可得到BE 的长即为BP PE +的最小值,设DE x =,在Rt BCE 中,利用勾股定理可得2x =,则棱长为22,进而可求得正四面体的外接球的表面积 【详解】将侧面ABC 和ACD △沿AC 边展开成平面图形,如图所示,菱形ABCD ,在菱形ABCD 中,连接BE ,交AC 于点P ,则BE 的长即为BP PE +的最小值,即14BE =因为正四面体ABCD ,所以AC AB =,所以120BCD ∠=︒, 因为E 是棱AD 的中点,所以30DCE ∠=︒, 所以90BCE BCD DCE ∠=∠-∠=︒, 设DE x =,则2AB BC CD AD x ====, 所以3CE x =,则22714BE BC CE x =+=所以2x =,则正四面体ABCD 的棱长为22623=所以该正四面体外接球的表面积为24312S ππ==,故选:A 【点睛】本题考查线段和最短问题,考查外接球问题,考查运算能力6.已知函数2()f x x ax b =++,,m n 满足m n <且()f m n m =-,()f n m n =-,则当m x n <<时,有( ) A .()f x x n +< B .()f x x m +> C .()0f x x -< D .()0f x x ->【答案】A【解析】设(,)(,)A m n m B n m n --,,写出直线AB 的方程,可知其斜率为负;又因为()f x 开口向上,所以在m x n <<时,()2f x x m n <-++,进而变形得出答案. 【详解】解:设(,)(,)A m n m B n m n --,,则直线AB 的方程为2y x m n =-++,即A ,B 为直线2y x m n =-++与()f x 的图像的两个交点,由于()f x 图像开口向上,所以当m x n <<时,()2f x x m n <-++,即()f x x x m n n +<-++<;故选:A. 【点睛】本题考查二次函数的性质,考查运算求解能力,属于基础题型. 7.将函数44()sin cos f x x x =+的图像向左平移8π个单位长度后,得到()g x 的图像,若函数()y g x ω=在[,]124ππ-上单调递减,则正数ω的最大值为 A .12B .1C .32D .23【答案】A【解析】先化简()f x 的表达式,平移后得到()g x 的解析式,再求出()g x ω的解析式,然后利用()g x ω的单调减区间列不等式组,求得ω的取值范围,进而求得正数ω的最大值. 【详解】依题意,()2221cos 21cos 21cos 23cos 42224x x x x f x -+++⎛⎫⎛⎫=+== ⎪ ⎪⎝⎭⎝⎭,向左平移π8个单位长度得到31π31π31cos 4cos 4sin 444844244x x x ⎡⎤⎛⎫⎛⎫++=++=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.故()()31sin 444g x x ωω=-,下面求函数的减区间:由ππ2π42π22k x k ω-+≤≤+,由于0>ω故上式可化为ππππ8282k k x ωω-++≤≤,由于函数()g x ω在,124ππ⎡⎤-⎢⎥⎣⎦上单调递减,故πππ8212πππ824k k ωω⎧-+⎪≤-⎪⎪⎨⎪+⎪≥⎪⎩,解得362122kk ωω⎧≤-⎪⎪⎨⎪≤+⎪⎩,所以当0k =时,12ω=为正数ω的最大值.故选A. 【点睛】本小题主要考查三角函数降次公式,考查三角函数图像变化的知识,考查三角函数的单调区间的求法,综合性较强,需要较强的运算能力.44sin cos x x +是不能够直接合并起来的,需要通过运用降次公式两次,才能化简为()sin A x B ωϕ++的形式.求解三角函数单调区间时,要注意A 是正数还是负数.8.在平面直角坐标系xOy 中,过点(1,4)P ,向圆C :222()5x m y m -+=+(16m <<)引两条切线,切点分别为A 、B ,则直线AB 过定点( ) A .1(,1)2-B .3(1,)2-C .13(,)22-D .1(1,)2-【答案】B【解析】在平面直角坐标系xOy 中,过点()1,4P ,向圆C :()2225x m y m -+=+(16m <<)引两条切线,则切线的长为==∴以点P 为圆心,切线长为半径的圆的方程为()()2214122x y m -+-=-∴直线AB 的方程为()()()222221427x m y x y m m ⎡⎤-+--+-=+-⎣⎦,即(1)(45)0m x x y +-+-=∴令10{450x x y +=+-=,得1{32x y =-=∴直线AB 恒过定点3(1,)2- 故选B.9.已知函数1(){}f x x x=-,其中{}x 为不小于x 的最小整数,如{}3.54=,{}33=,则关于()f x 性质的表述,正确的是( ) A .定义域为()(),00,-∞⋃+∞ B .在定义域内为增函数 C .函数为周期函数 D .函数为奇函数【答案】C【解析】只需要研究分母对应的函数(){}g x x x =-即可.求出定义域排除A 选项;利用周期函数的定义得出(1)()g x g x +=,故函数是周期函数,由此排除B 选项,C 选项正确;利用奇函数定义容易得到D 选项错误. 【详解】解:易知{}0x x -≠,故定义域为{|}x x Z ≠,故A 选项错误,令(){}g x x x =-,易知(1){1}(1){}11{}()g x x x x x x x g x +=+-+=+--=-=, 故{}f x 是以1为周期的函数,故C 选项正确,B 项错误, 因为()()f x f x --≠,故D 选项错误. 故选:C . 【点睛】本题考查新定义问题,涉及对函数周期性、单调性、奇偶性等知识,同时考查分析问题与解决问题的能力.二、多选题10.已知圆O :224x y +=和圆C :22231x y .现给出如下结论,其中正确的是( )A .圆O 与圆C 有四条公切线B .过C 且在两坐标轴上截距相等的直线方程为5x y +=或10x y -+= C .过C 且与圆O 相切的直线方程为916300x y -+=D .P 、Q 分别为圆O 和圆C 上的动点,则PQ 3+3 【答案】AD【解析】对于A ,先由已知判断两圆的位置关系,从而可判断两圆的公切线的条数; 对于B ,截距相等可以过原点或斜率只能为1-,从而可得直线方程; 对于C ,由于点C 在圆O 外,所以过点C 与圆O 相切的直线有两条;对于D ,PQ 的最大值为圆心距与两圆半径的和,最小值为圆心距与两圆半径的差, 【详解】解:由题意可得,圆O :224x y +=的圆心为(0,0)O ,半径12r =,圆C :22231x y 的圆心(2,3)C ,半径21r =,因为两圆圆心距121321OC r r =>+=+, 所以两圆相离,有四条公切线,A 正确;截距相等可以过原点或斜率只能为1-,B 不正确; 过圆外一点与圆相切的直线有两条,C 不正确;PQ 的最大值等于12OC r r ++,最小值为12OC r r --,D 正确.故选:AD 【点睛】此题考查两圆的位置关系的有关性质,属于基础题11.如图,在四棱锥E ABCD -中,底面ABCD 是边长为2的正方形,CDE △是正三角形,M 为线段DE 的中点,点N 为底面ABCD 内的动点,则下列结论正确的是( )A .若BC DE ⊥,则平面CDE ⊥平面ABCDB .若BC DE ⊥,则直线EA 与平面ABCD 所成的角的正弦值为64C .若直线BM 和EN 异面,则点N 不可能为底面ABCD 的中心D .若平面CDE ⊥平面ABCD ,且点N 为底面ABCD 的中心,则BM EN = 【答案】ABC【解析】根据面面垂直的判定,线面夹角的求解办法,以及异面直线的定义,结合面面垂直的性质,对每个选项进行逐一分析,即可容易判断选择. 【详解】∵BC CD ⊥,BC DE ⊥,CDDE D =,,CD DE ⊂平面CDE ,∴BC ⊥平面CDE ,∵BC ⊂平面ABCD ,∴平面ABCD ⊥平面CDE ,A 项正确;设CD 的中点为F ,连接EF 、AF ,则EF CD ⊥. ∵平面ABCD ⊥平面CDE ,平面ABCD平面CDE CD =,EF ⊂平面CDE∴EF ⊥平面ABCD ,设EA 与平面ABCD 所成的角为θ,则EAF θ=∠, 223EF CE CF =-=225AF AD FD =+=,222AE EF AF =+= 则6sin EF AE θ==,B 项正确; 连接BD ,易知BM ⊂平面BDE ,由B 、M 、E 确定的面即为平面BDE , 当直线BM 和EN 异面时,若点N 为底面ABCD 的中心,则N BD ∈, 又E ∈平面BDE ,则EN 与BM 共面,矛盾,C 项正确;连接FN ,∵FN ⊂平面ABCD ,EF ⊥平面ABCD ,∴EF FN ⊥, ∵F 、N 分别为CD 、BD 的中点,则112FN BC ==, 又3EF=222EN EF FN =+=,227BM BC CM =+则BM EN ≠,D 项错误. 故选:ABC . 【点睛】本题综合考查面面垂直的判定以及性质、异面直线的定义、线面夹角的求解,属综合困难题.12.已知函数()()sin sin f x x x π=+,现给出如下结论,其中正确的是( ) A .()f x 是奇函数B .()f x 是周期函数C .()f x 在区间()0,π上有三个零点D .()f x 的最大值为2【答案】AC【解析】根据奇函数的定义和周期函数的定义,函数的零点等价于方程的根,反证法求函数最值,即可得答案;∵x ∈R ,()()()()sin sin sin sin f x x x x x f x ππ-=-+-=--=-, ∴()f x 是奇函数,A 正确;sin y x =的周期12T k π=,k ∈Z ,()sin y x π=的周期22T n =,n ∈Z ,∵{}{}1122|2,|2,T T k k T T n n π=∈=∈=∅Z Z ,∴()f x 不是周期函数,B 错误;令()()sin sin 0f x x x π=+=,得()()sin sin sin x x x π=-=-, ∴2x x k ππ=-+,k ∈Z ,或2x x k πππ-=+,k ∈Z , 解得21k x ππ=+,k ∈Z 或()211k x ππ+=-,k ∈Z ,又()0,x π∈,21x ππ=+或41x ππ=+或1x ππ=-,C 正确; 当sin 1x =时,22x k ππ=+,k ∈Z ,当()sin 1x π=时,122x k =+,k ∈Z , ∵12,2,22x x k k x x k k ππ⎧⎫⎧⎫=+∈⋂=+∈=∅⎨⎬⎨⎬⎩⎭⎩⎭Z Z , 即sin y x =与()sin y x π=不可能同时取得最大值1,故D 错误. 故选:AC . 【点睛】本题考查根据三角函数的解析式求函数的性质,考查函数与方程思想,考查逻辑推理能力、运算求解能力.三、填空题13.若两个非零向量a 、b 满足()()0a b a b +⋅-=,且2a b a b +=-,则a 与b 夹角的余弦值为__________. 【答案】35【解析】设平面向量a 与b 的夹角为θ,在等式2a b a b +=-两边平方,再利用向量的数量积运算,即可得答案;设平面向量a 与b 的夹角为θ,∵()()22220a b a b a b a b+⋅-=-=-=,可得a b =,在等式2a b a b +=-两边平方得22222484a a b b a a b b +⋅+=-⋅+, 化简得3cos 5θ=. 【点睛】本题考查向量夹角公式和数量积运算,考查逻辑推理能力、运算求解能力.14.函数y =__________.【答案】【解析】根据两点之间的距离公式改写目标函数解析式,即可根据几何意义求得结果. 【详解】因为y ==其几何意义为点(),0Px 到点()1,1A -、()2,2B 两点的距离之和,()1,1A -关于x 轴的对称点()1,1C --, ||||||||||y PA PB PC PB BC =+=+≥当且仅当B 、P 、C 三点共线时y 的值最小为BC ==故答案为:【点睛】本题考查两点之间距离公式的妙用,涉及函数最值的求解,属基础题.15.如图,正方体1111ABCD A B C D -的棱长为1,中心为O ,12BF BC =,1114A E A A =,则四面体OEBF 的体积为__________.【答案】196【解析】根据中心的特点,结合点E 的位置,求得E 到平面OBF 的距离和A 到平面OBF 距离的关系,结合三角形OBF 是直角三角形,即可求得棱锥体积.【详解】根据题意,连接11,A B D C ,如下所示:因为O 是正方体的中心,故O 在平面11A D CB 中. 点E 满足1114A E A A =, 故点E 到平面OBF 的距离为点A 到平面OBF 距离的14. 故三棱锥E OBF -的高122428h =⨯=. 又容易知三角形OBF 是角OFB ∠为直角的直角三角形, 且112122OF A B BF ===, 故三角形OBF 的面积112222S =⨯=.故四面体OEBF 的体积111338896V S h =⨯⨯=⨯=. 故答案为:196. 【点睛】本题考查棱锥体积的求解,注意本题中正方体中心的性质,属基础题.16.已知圆O :221x y +=直线l :2y x a =+,过直线l 上的点P 作圆O 的切线PA ,PB ,切点分别为A ,B ,若存在点P 使得32PA PB PO +=,则实数a 的取值范围是______.【答案】[-【解析】取AB 中点C ,则,,O P C 三点共线,且OP AB ⊥,由已知可得322PC PO =,即3||||4PC PO =,利用Rt PAO Rt ACO △△,求出||PO ,要使得点P 存在,坐标原点O 到直线l 的距离不大于||PO 的值,建立a 的不等量关系,求解即可. 【详解】连,,,AB OA OB OP ,直线PA ,PB 是圆O 的切线,切点分别为A ,B ,||||,PA PB PC AB ∴=∴⊥, ||||,,,,OA OB OC AB O C P =∴⊥∴三点共线,AC OP ∴⊥,24331,,||||24PA PB PC PO PC PO OC OP +===∴=, ||||,||||OA OP Rt PAO Rt ACO OC OA ∴=△△, 221||||1,||24||||O OP OA OP C OP ∴==∴==⋅, 要使在直线l 上存在点P 使得||2OP =,则点O 到直线l 的距离2≤d ,2,||d a =≤≤a ∴-≤≤故答案为:[- 【点睛】本题考查直线与圆的位置关系以及切线性质的应用,注意平面几何知识和向量知识的合理利用,考查数形结合思想,属于中档题.四、解答题17.在平面直角坐标系xOy 中,动点(),P x y 到两坐标轴的距离之和等于它到定点()1,1A 的距离,记点P 的轨迹为C .(1)求点P 的轨迹C 的方程并作出动点P 的轨迹的图形; (2)设(),Q x y 是轨迹C 上的任意一点,求: ①2x y +的最大值; ②22xy +的最小值.【答案】(1)答案见解析;(2)①2;②6-【解析】(1)动点P 到两坐标轴的距离之和等于它到定点()1,1A 的距离,即可得到方程10xy x y ++-=,讨论xy 与0的大小去绝对值,即得轨迹方程,根据相应的范围画出轨迹图形即可;(2)利用2x y +、22x y +与P 的轨迹C 的几何意义可求最值【详解】(1)由动点(),P x y 到两坐标轴的距离之和等于它到定点()1,1A 的距离∴x y +=10xy x y ++-=当0xy ≥时,可得10xy x y ++-=,即11x y x -=+,故211y x=-++(1x <-或01)x ≤≤当0xy <时,10xy x y -++-=,即()1)0(1x y --=,故1(0)x y =<或1(0)y x =<动点P 的轨迹为:(2)①设2x y t +=,依t 的几何意义:直线20x y t +-=与P 的轨迹有交点的情况下,在x 或y 轴上的截距最大即可∴当20x y t +-=过(0,1)时2x y +有最大值为2②设22x z y +=,依z 的几何意义:圆222x y r +=与P 的轨迹有交点的情况下,半径r 最小的情况∴当222x y r +=与211y x=-++在01x ≤≤分支相切时,22x y +有最小值,切点为221)-,22r =故z 的最小值为642-【点睛】本题考查了动点轨迹的方程及其图形,利用代数式与轨迹图形的几何意义求它们的最值,注意找到图形中出现最值的边界点18.如图,在平面直角坐标系中,角αβ,的始边均为x 轴正半轴,终边分别与圆O交于A ,B 两点,若712παπ∈(,),12πβ=,且点A 的坐标为1A m -(,).(1)若423tan α=-,求实数m 的值; (2)若34tan AOB ∠=-,若sin2α的值.【答案】(1)12m =(27243- 【解析】(1)由题意利用二倍角的正切公式求得tan α的值,再利用任意角的三角函数的定义求得m 的值.(2)利用同角三角函数的基本关系,求得12sinπα-()和12cosπα-()的值,再利用两角和的正弦公式求得2266sin sin ππαα⎡⎤=-+⎢⎥⎣⎦()的值.【详解】(1)由题意可得224213tan tan tan ααα==--,12tan α∴=-,或2tan α=.712παπ∈(,),12tan α∴=-,即112m =--,12m ∴=. (2)sin 312124cos 12tan AOB tantan παπαβαπα⎛⎫- ⎪⎝⎭∠=-=-==-⎛⎫- ⎪⎝⎭()(), 22111,,121212212sin cos πππππααα⎛⎫⎛⎫⎡⎤-+-=-∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 34125125sin cos ππαα∴-=-=-(),(), 24226121225sin sin cos ()()()πππααα∴-=--=-,2722161225cos cos ππαα-=--=()(),7243222266666650sin sin sin cos cos sin ππππππαααα-⎡⎤∴=-+=-+-=⎢⎥⎣⎦()()().【点睛】本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,二倍角的正弦公式,用两角和的正弦公式的应用,属于中档题.19.如图1,图2,在矩形ABCD 中,已知2AB =,3AD =,点E ,F 分别在AD ,CD 上,且1AE CF ==,将四边形ABCE 沿EC 折起,使点B 在平面CDE 上的射影H 在直线DE 上.(1)求证:CD BE ⊥; (2)求证://HF 平面ABCE ;(3)求直线AC 与平面CDE 所成角的正弦值. 【答案】(1)证明见解析;(2)证明见解析;(3213. 【解析】(1)推导出BH CD ⊥,CD DE ⊥,从而CD ⊥平面DBE ,由此能证明CD BE ⊥.(2)设BH h =,EH k =,过F 作FG 垂直ED 于点G ,由勾股定理得线段2BH =.推导出//HF EC ,由此能证明//HF 平面ABCE .(3)延长BA 交BE 于点M ,点A 到平面EFCD 的距离为点B 到平面EFCD 距离的13,点A 到平面EFCD 的距离为23,由此能求出直线AF 与平面EFCD 正弦值.【详解】(1)∵BH ⊥平面CDE ,∴BH CD ⊥, 又CD DE ⊥,BHDE H =,∴CD ⊥平面DBE ,∵BE ⊂平面DBE ,∴CD BE ⊥. (2)设BH x =,EH y =,由(1)知CDB △为直角三角形,在BHE 与CDB △中有()2222225,223,x y x y ⎧+=⎪⎨+-+=⎪⎩ 解方程得2,1,x y =⎧⎨=⎩,∴H 为DE 的中点.又F 为CD 中点,∴//HF CE ,且HF ⊄平面ABCE ,CE ⊂平面ABCE , ∴//FH 平面ABCE .(3)在梯形ABCE 中,延长BA 交CE 于点M , ∵::1:3AE BC MA MB ==,.点A 到平面CDE 的距离为点B 到平面CDE 距离的13, ·点A 到平面CDE 的距离为23,而13AC =, 故直线AC 与平面CDE 所成角的正弦值为21339.【点睛】本题考查线面垂直、线面平行的证明,考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想、数形结合思想,是中档题. 20.已知2244log log 02x x ++⋅≤. (1)求x 的取值的集合A ; (2)x A ∈时,求函数()1342x x f x ++=-的值域;(3)设()21,032,2,20,x x g x x x ⎧-≤≤=⎨+-≤<⎩若()y g x a =-有两个零点1x 、2x (12x x <),求1ax 的取值范围.【答案】(1){}|25A x x =-≤≤;(2)[]4,3840-;(3)[]1,0-.【解析】(1)利用对数运算,化简不等式,结合对数函数单调性,求解不等式即可; (2)根据(1)中所求,将()f x 配凑为关于2x 的二次函数,求其值域即可;(3)根据题意,用1x 表示出a ,求出1x 的范围,再求目标式的范围即可.【详解】(1)由2244log log 023x x ++⋅≤得, ()()222log 41log 4log 90x x +-+-≤⎡⎤⎡⎤⎣⎦⎣⎦,∴()221log 4log 9x ≤+≤,∴25x -≤≤,故{}|25A x x =-≤≤为所求.(2)当x A ∈时,()1342x x f x ++=-()()2242824214x x x =⋅-⋅=--, ∵25x -≤≤,∴12324x ≤≤, ∴()43840f x -≤≤,即为()f x 的值域.(3)作出函数()g x 的图象,∵()y g x a =-有两个零点1x 、2x 且12x x <,∴120x -≤<,02a ≤<,且()112a f x x ==+,∴()()()2111111211ax f x x x x x ==+=+-,∵120x -≤<,∴110ax -≤≤即1ax 的取值范围为[]1,0-.【点睛】本题考查对数运算、对数不等式的求解,对数型复合函数值域的求解,以及对数函数图像的应用,属综合中档题.。
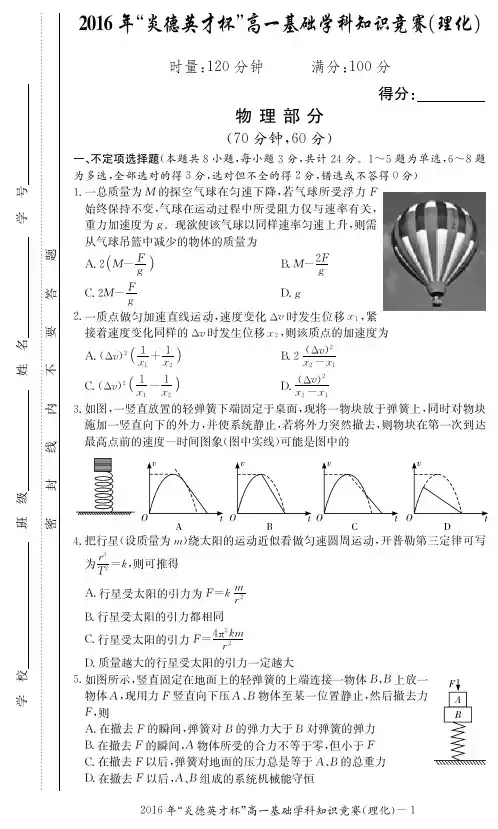
2020年“炎德英才杯”高一基础学科知识竞赛物理时量:90分钟满分:100分一、单项选择题:本题共8小题,每小题3分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.牛顿时代的科学家们围绕万有引力的研究,经历了大量曲折顽强而又闪烁智慧的科学实践。
在万有引力定律的发现历程中,下列叙述符合史实的是A.伽利略研究了第谷的行星观测记录,提出了行星运动定律B卡文迪许将行星与太阳、地球与月球、地球与地面物体之间的引力推广到宇宙中的一切物体,得出了万有引力定律C.哈雷在实验室中准确地得出了引力常量G的数值,使得万有引力定律有了现实意义D.牛顿通过月地检验,验证了万有引力定律2.甲,乙两物体同时以相同的速度经过某个位置时开始计时,从t=0时刻开始两物体沿同一直线做减速运动,最终又都停止在另一相同的位置,整个过程甲、乙运动的v-t图象如图所示,则A.整个过程中甲的平均速度大于乙的平均速度B.从t=0时刻到下一次速度相等的过程中,乙的平均速度要大于甲的平均速度C.在运动过程中甲的加速度一直小于乙的加速度D.在运动过程中甲,乙两物体的加速度不可能相同3.如图所示,重物M沿竖直杆下滑,并通过一根不可伸长的细绳带动小车沿水平面向右运动。
若当滑轮右侧的绳与竖直方向成β=60°角,且重物下滑的速率为v=2m/s时,滑轮左侧的绳与水平方向成α=45°角,则小车的速度为A.23m/sB.3m/sC.22m/sD.2m/s4.在一斜面頂端,将质量相等的甲、乙两个小球分别以2v 和v 的速度沿同一方向水平抛出,两球都落在该斜面上。
则下列说法正确的是A 乙球落到斜面上时速度方向与水平方向的夹角要比甲球的小B.从抛出到落到斜面上重力对甲,乙两球做功之比为1:2C.落到斜面上时甲,乙两球重力的瞬时功率之比为1:2D.两球从抛出到落到斜面上运动的时间相同5.2019年春节期间,中国科幻电影里程碑作品《流浪地球》热播,影片中为了让地球逃离太阳系,人们在地球上建造特大功率发动机,使地球完成一系列变轨操作,其逃离过程可设想成如图所示,地球在椭圆轨道I 上运行到远日点B 变轨,进入圆形轨道II 。
2019-2020学年湖南省炎德英才杯2019级高一下学期基础学科知识竞赛英语试卷★祝考试顺利★(解析版)时量:100分钟满分:100分第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项。
AHigh school is more than just attending classes and trying to get good grades. Students can take full advantage of the opportunities high school offers them to explore their interests and interact with fellow students in activities and clubs. Honor SocietiesFor students who do well academically or artistically, there are organizations like the National Honor Society, National Science Honor Society and National Art Honor Society that reward students whose achievements are superior. Students who desire to be a part of high school honor societies are required to have grade point averages of at least 3.0, on a 4.0 scale, and may have to get nominated(提名)by teachers or request recommendation letters. While these organizations focus on scholarship, they also teach members leadership skills and encourage community service.Sports and Athletics ClubsWhether formally joining a sports team or simply participating in school activities, high schools offer students a wide range of sports and athletics clubs. Helping students stay active and healthy, these clubs teach students the importance of teamwork, patience and practice.Community Service OrganizationsOrganizations like the Key Club International and Habitat for Humanity help students give back to their communities by participating in structured service learning activities. From cleaning a local park to distributing(分配)Thanksgivingbaskets to the homeless, these organizations teach children the importance of reaching out a helping hand to those in need.Career Development ClubsDetermining the right career path comes from exploring different options to learn what each career requires and how it fits your interests. High schools develop clubs and organizations dedicated to students who want to own businesses, become teachers, doctors, lawyers and actors, among many other careers. Students participating in these clubs are active in the community and often compete against students on local, regional and sometimes national levels. Clubs like DECA(an association of marketing students) and FBLA(Future Business Leaders of America) have students compete against one another to test their business skills. Other career-oriented clubs include organizations for future teachers, debate and photography enthusiasts.1. Which of the following has a requirement for student achievements?A. Career Development Clubs.B. Honor Societies.C. Community Service Organizations.D. Sports and Athletics Clubs.2. What do Sports and Athletics Clubs and Community Service Organizations have in common?A. They both need students to work together.B. They both teach students practical skills.C. They both provide moral education for students.D. They both build students' confidence.3. What is the purpose of Career Development Clubs?A. To help students with career planning.B. To train people for all walks of life.C. To lead students to find their hobbies.D. To improve students' awareness of competition.B"Nature never stops being amazing," says Rosemary Mosco, master of humorous nature art. Her new book, Birding Is MyFavorite Video Game, combines fascinating facts with。
2019-2020学年湖南省炎德英才杯2019级高一下学期基础学科知识竞赛
数学试卷
★祝考试顺利★
(解析版)
时量:120分钟满分:100分
一、单项选择题(本题共8小题,每小题3分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)
1.已知集合A={x|2x>2},B={y|y=x2,x∈R},则(
R
A)∩B=
A[0,1) B.(0,2) C.(-∞,1] D.[0,1]
2.设f(x)是定义域为R的偶函数,且f(x+3)=f(x-1),若当x∈[-2,0]时,f(x)=2-x,记a=
f(log
21
4
),b=f(3),c=f(32),则a,b,c的大小关系为
Aa>b>c B.c>b>a C.c>a>b D.a>c>b
3.在△ABC中,D是边AC上的点,且AD=AB,BD=3AB,BC=2BD,则sinC的值为
A 1
2
B.
1
4
C.
1
8
D.
1
12
4.如图,圆O是边长为23的等边三角形ABC的内切圆,其与BC边相切于点D,点M为圆O上任意一点,若BM xBA yBD
=+(x,y∈R),则2x+y的最大值为
232
5.如图,正四面体ABCD中,E是棱AD的中点,P是棱AC上一动点,BP+PE14则该正四面体的外接球的表面积是
A.12π
B.32π
C.8π
D.24π
6.已知函数f(x)=x 2+ax +b,m,n 满足m<n 且f(m)=n -m,f(n)=m -n,则当m<x<n 时,有 Af(x)+x<n B.f(x)+x>m C.f(x)-x<0 D.f(x)-x>0
7.将函数f(x)=sin 4x +cos 4x 的图象向左平移8π个单位长度后,得到g(x)的图象,若函数y =g(ωx)在[,124ππ-
]上单调递减,则正数ω的最大值为 A.12 B.1 C.32 D.23
8.在平面直角坐标系xOy 中,过点P(1,4),向圆C :(x -m)2+y 2=m 2+5(1<m<6)引两条切线,切点分别为A 、B,则直线AB 过定点
A(-12,1) B(-1,32) C(-12,32) D.(-1,12
) 二、多项选择题(本题共4小题,每小题4分,共16分。
在每小题给出的四个选项中,有多项符合题目要求。
全部选对的得4分,部分选对的得2分,有选错的得0分。
)
9.已知圆O :x 2+y 2=4和圆C :(x -2)2+(y -3)2=1。
现给出如下结论,其中正确的是 A 圆O 与圆C 有四条公切线
B 过
C 且在两坐标轴上截距相等的直线方程为x +y =5或x -y +1=0
C 过C 且与圆O 相切的直线方程为9x -16y +30=0
D.P 、Q 分别为圆O 和圆C 上的动点,则|PQ|的最大值为13+3,最小值为13-3
10.如图,在四棱锥E -ABCD 中,底面ABCD 是边长为2的正方形,△CDE 是正三角形,M 为线段DE 的中点,点N 为底面ABCD 内的动点,则下列结论正确的是。