函数间断点分类及类型共20页文档

名词解释--函数的间断点
函数的间断点指的是函数在定义域内存在某些点，使得函数在这些点上失去定义或者函数在这些点上不连续。

在数学中，函数的间断
点分为三类：可去间断点、跳跃间断点和无穷间断点。

可去间断点是指函数在该点上失去定义，但是通过修改或者定义该点的函数值后，可以使函数在该点上连续。

例如函数f(x) = (x^2 - 1)/(x-1)在x=1处具有可去间断点，因为分母为0导致函数在该点上
无定义，但若定义f(1)=2，则函数在x=1处是连续的。

跳跃间断点是指函数在某点的左右极限存在，但是极限值不相等，导致函数在该点上不连续。

例如函数f(x) = [x]（表示向下取整）在整数点上具有跳跃间断点，因为在整数点左右极限存在，但在整数点
上函数值不同，造成函数的断裂。

无穷间断点是指函数在某点的左右极限至少有一个趋近于无穷大（正无穷大或负无穷大），导致函数在该点上不连续。

例如函数f(x) = 1/x在x=0处具有无穷间断点，因为当x趋近于0时，函数的极限为无穷大。

函数间断点及类型
函数间断点是指函数在某些点上不连续的现象，主要有三种间断类型：可去间断、跳跃间断和无穷间断。

可去间断是指函数在某个点上存在一个极限值，但是该点上的函数值与极限值不相等。

这种间断可以通过修正函数来消除，也就是说，在该点上定义函数值为极限值即可。

跳跃间断是指函数在某个点的左右极限值存在且不相等，导致函数在该点上产生一个跳跃。

这种间断可以通过定义函数的左右极限值来消除。

无穷间断是指函数在某个点上的极限值为正无穷或负无穷，这种间断也可以通过定义函数的极限值来消除。

函数间断点及其类型是函数分析中的重要概念，对于理解函数的性质和行为有着重要的意义。

- 1 -。

间断点的分类及判断方法间断点是指在曲线或者函数图像上出现的不连续的点，它们在数学、物理、工程等领域中都有着重要的意义。

对于间断点的分类和判断方法，我们需要进行深入的研究和探讨。

首先，我们来看间断点的分类。

按照函数图像的性质，间断点可以分为三类，第一类是可去间断点，第二类是跳跃间断点，第三类是无穷间断点。

可去间断点是指在该点处函数的极限存在，但函数在该点处的值与极限值不相等。

通常来说，可去间断点是由于函数在该点处没有定义或者定义与极限值不相等所导致的。

在图像上，可去间断点表现为一个空心圆点。

跳跃间断点是指在该点处函数的左极限和右极限存在，但左右极限不相等。

这种间断点通常出现在分段函数的转折处，图像上表现为一个实心圆点。

无穷间断点是指在该点处函数的极限为无穷大或者负无穷大。

在图像上，无穷间断点表现为一个竖直的渐近线。

接下来，我们来谈谈判断间断点的方法。

对于可去间断点，我们可以通过代数方法来判断，即在该点附近对函数进行化简，看是否可以消去分母或者化简为同一表达式。

如果可以化简，则该点为可去间断点；如果不能化简，则不是可去间断点。

对于跳跃间断点，我们可以通过左极限和右极限来判断。

如果左极限不等于右极限，则该点为跳跃间断点；如果左极限等于右极限，则不是跳跃间断点。

对于无穷间断点，我们可以通过极限的性质来判断。

如果在该点的左右极限中至少有一个为无穷大或者负无穷大，则该点为无穷间断点；如果左右极限都有限，则不是无穷间断点。

综上所述，间断点的分类及判断方法对于我们理解函数图像的性质和特点具有重要的意义。

通过对间断点的深入研究，我们可以更好地理解函数的性质，为数学和物理等领域的应用提供更加准确的理论支持。

希望本文的介绍能够对大家有所帮助。

高等数学之函数间断点判断方法总结
若f(x)函数在点X0处不连续，则称点X0为函数f(x)的不连续点或间断点，函数间断点的分类如下：
•第一类间断点：函数f（x）在X0处的左极限和右极限都存在
第一类间断点包含以下两类：
（1）可去间断点：函数f（x）在X0处的左极限等于右极限；
（2）跳跃间断点：函数f（x）在X0处的左极限不等于右极限；
•第二类间断点：函数f（x）在X0处的左极限和右极限至少有一个不存在。

方法总结：判断函数间断点的类型，关键在于看函数在间断点处的左右极限是否存在。

例一：
分析：本题要确定参数a的值，使得当参数a为不同值时，函数在0点连续，或在0点为可去间断点。

解决这一类题的方法就是严格扣住函数连续和可去间断点的定义。

解：
备注：做这类题一定要扣住定义。

例2：
分析：x=0为函数f(x)的第二类间断点，则当x趋于0时，函数f(x)的极限不存在；x=1为函数f(x)的可去间断点，则当x趋于1时，函数f(x)的极限存在。

解：。

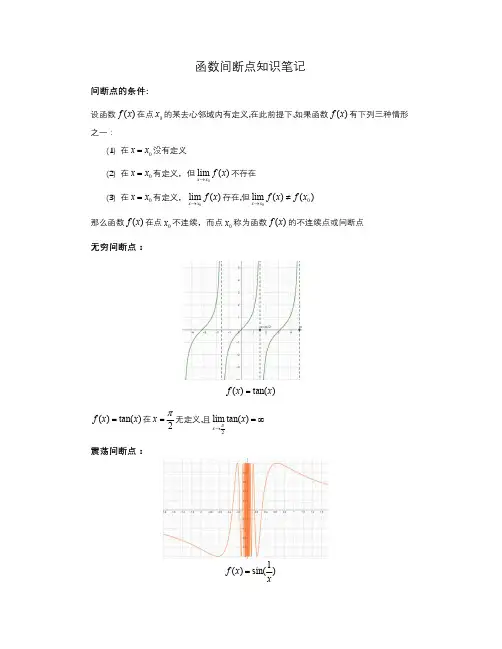
函数间断点知识笔记间断点的条件:设函数()f x 在点0x 的某去心邻域内有定义,在此前提下,如果函数()f x 有下列三种情形之一：(1) 在0x x 没有定义(2) 在0x x 有定义，但0lim ()x x f x 不存在 (3) 在0x x 有定义，0lim ()x x f x 存在,但00lim ()()x x f x f x 那么函数()f x 在点0x 不连续，而点0x 称为函数()f x 的不连续点或间断点无穷间断点：()tan()f x x()tan()f x x 在2x 无定义,且2lim tan()x x 震荡间断点：1()sin()f x x1()sin(f x x在点0x 没有定义,当0x 时，函数值在1 和-1之间变动无限多次 可去间断点：（图不是很好看）21()1x f x x 21()1x f x x 在点1x 没有定义，但在这里有2111lim =lim(1)21x x x x x 如果补充定义:令(1)2f 那么函数在点1x 成为连续，这种情况间断点为可去间断点 同例有函数:,1,()1, 1.2x x f x x ，这里就不论述了. 跳跃间断点：1,0,()0,0,1,0.x x f x x x x当0x 时,0000lim ()lim (1)1lim ()lim (1)1x x x x f x x f x x左右极限都存在但不相等,故0lim ()x f x 不存在,因图像在0x 处产生跳跃现象，该类间断点成为跳跃间断点第一类间断点：左极限0()f x 和0()f x 都存在的间断点（跳跃间断点和可去间断点）第二类间断点：非第一类间断点的所有间断点.(无穷间断点和震荡间断点)。

函数间断点及类型
函数间断点指的是函数在某些点上失去连续性的现象。

一般来说，这种现象可能由以下几种情况引起：
1. 可去间断点：在该点上，函数存在极限值，但不连续。

2. 跳跃间断点：在该点上，左右极限值不等。

3. 本质间断点：在该点上，函数既不存在极限值，也不连续。

对于这些不同类型的间断点，我们可以通过不同的方法来判断它们的性质和特点。

比如，对于可去间断点，我们可以通过极限值来确定它的性质；而对于跳跃间断点和本质间断点，则需要通过左右极限值的大小比较和函数的形态来判断它们的性质。

总结函数连续与间断的概念,函数间断点的分类
函数连续概念：
函数的连续概念是指满足一定条件的函数的自变量的取值可以从一个
无穷小的值逐步连续变化，而变量的函数值也不断变化，但是这个变化是
自然、合理的，没有断裂、跳跃，也没有停止这样的变化。

函数间断点概念：
函数间断点是指函数的自变量取一定的值时，函数值发生突变，跳跃
或者折返，函数发生突变点，也叫函数间断点
函数间断点分类：
1.自变量的极值点。

当自变量取此点值时，函数值不可能再增加或减小。

2.拐点。

当自变量取该点值时，函数的图像由箭头向上转折为向下，
或者由箭头向右转折为向左。

3.对称轴经过的点。

函数是有对称轴经过的，在对称轴经过的点时，
函数值发生突变。

4.不可导点。

在不可导点，函数即发生了突变，又出现不可导的情况。

高数间断点的分类及判断方法
首先，我们来看间断点的分类。

在高等数学中，间断点可以分为三类，可去间断点、第一类间断点和第二类间断点。

可去间断点是指函数在该点处存在有限极限，但是函数在该点处没有定义或者定义与极限值不相等。

第一类间断点是指函数在该点处左右极限存在，但是左右极限不相等，因此函数在该点处不存在极限。

第二类间断点是指函数在该点处左右极限至少有一个不存在或者无穷大，因此函数在该点处不存在有限极限。

接下来，我们来介绍间断点的判断方法。

对于可去间断点，我们可以通过函数在该点附近的表达式进行化简，如果能够消去分母中的因式，则函数在该点处存在有限极限，因此是可去间断点。

对于第一类间断点，我们可以通过左右极限的大小关系进行判断，如果左右极限不相等，则函数在该点处存在第一类间断点。

对于第二类间断点，我们可以通过左右极限的存在性进行判断，如果左右极限至少有一个不存在或者为无穷大，则函数在该点处存在第二类间断点。

在实际应用中，我们可以通过以上的分类和判断方法，对函数的间断点进行准确的判断和分析。

这对于理解函数的性质和图像的特征，以及解决实际问题具有重要的意义。

总之，高数间断点的分类及判断方法是高等数学中的重要知识点，对于理解函数的性质和图像的特征具有重要的作用。

通过系统地学习和掌握，我们能够更好地应用这一知识点，解决实际问题，提高数学建模能力。

希望本文的介绍能够帮助大家更好地理解和掌握高数间断点的分类及判断方法。

（精编资料推荐）函数间断点分类及类型
函数间断点（intermittent point）是指一个函数图像在某一点发生变化类型的点，
它可能出现在函数的任何一点，但却是某一特定的类型的变化点。

下面介绍函数间断点的
分类及类型。

1. 极大值和极小值断点
极大值断点指函数在该点的前后交替变换。

当函数的导数从正变为负，出现极大值断点，这种断点叫作极大值断点或山谷点；当函数的导数从负变为正，出现极小值断点，这
种断点叫作极小值断点或山峰点。

例如，函数f(x)=x^2-4x+4在（2，4）处有极小值断点。

2. 拐点
拐点指函数在此点处发生变换类型，也叫变换点或汽车变弯断点，它的关键特征是函
数的定义域发生变化，指函数级数的阶发生变化或者函数图像的弯曲发生变化。

例如，函
数f(x)=x^3-3x^2+x在（1，1）处有拐点。

3. 虚点
虚点是函数不可导的断点，也称它们为独立点，主要表现为函数导数定义域发生变化，但函数值的连续性不发生变化的点。

例如，函数f(x)=|x|在（0，0）处有虚点。

总之，函数间断点可以分为极大值和极小值断点、拐点、虚点和无穷值点。

它们差异
来自于函数临界点处函数定义域、导数在此点处取值情况以及函数等值线形状变化等特性。

函数不连续点的分类函数的连续性是数学中一个重要的概念，它描述了函数在某个点上的性质。

如果函数在某个点上连续，意味着函数在该点附近的取值变化平滑，没有突变或跳跃。

然而，并非所有的函数都是连续的，有些函数在某些点上是不连续的。

本文将介绍函数不连续点的分类。

一、第一类间断点第一类间断点是指函数在该点上的左右极限存在，但不相等。

也就是说，函数在该点的左右两侧有极限，但两个极限不相等。

这种情况下，函数在该点上的取值会出现跳跃。

例如，考虑函数f(x) = |x|，在x = 0处，函数的左极限为-1，右极限为1，两者不相等。

因此，函数f(x)在x = 0处是第一类间断点。

二、第二类间断点第二类间断点是指函数在该点上的左右极限至少有一个不存在。

也就是说，函数在该点的左右两侧至少有一个方向上的极限不存在。

例如，考虑函数g(x) = 1/x，在x = 0处，函数的左极限为负无穷，右极限为正无穷。

因为左右极限至少有一个不存在，所以函数g(x)在x = 0处是第二类间断点。

三、可去间断点可去间断点是指函数在该点上的左右极限存在且相等，但函数在该点上的取值与极限不相等。

也就是说，函数在该点的左右两侧有极限，且两个极限相等，但函数在该点上的取值与极限不相等。

例如，考虑函数h(x) = (x^2 - 1)/(x - 1)，在x = 1处，函数的左极限和右极限都为2。

然而，函数在x = 1处的取值为0，与极限不相等。

因此，函数h(x)在x = 1处是可去间断点。

四、无穷间断点无穷间断点是指函数在某个点上的极限为无穷大或无穷小。

也就是说，函数在该点的左右两侧的极限至少有一个是无穷大或无穷小。

例如，考虑函数k(x) = 1/x，在x = 0处，函数的左极限为负无穷，右极限为正无穷。

因为左右极限至少有一个是无穷大，所以函数k(x)在x = 0处是无穷间断点。

综上所述，函数的不连续点可以分为第一类间断点、第二类间断点、可去间断点和无穷间断点。

函数的间断点名词解释
函数的间断点是指函数在定义域内某一点处不连续的现象。

当函数在某一点的左右两侧的函数值存在差异，或者函数在该点处无定义，都可以称之为间断点。

函数的间断点可以分为三种类型：可去间断点、跳跃间断点和无穷间断点。

1. 可去间断点：当函数在某一点的左右两侧的函数值存在差异，但可以通过定义函数在该点处的函数值，使得函数在该点处连续。

这种情况下，该点被称为可去间断点。

2. 跳跃间断点：当函数在某一点的左右两侧的函数值存在差异，且无法通过定义函数在该点处的函数值使得函数在该点处连续。

这种情况下，该点被称为跳跃间断点。

3. 无穷间断点：当函数在某一点处趋于无穷大或无穷小，使得函数在该点处无定义，即函数在该点处不存在。

这种情况下，该点被称为无穷间断点。

函数的间断点在数学中具有重要意义，它可以帮助我们研究函数的性质和行为。

通过分析函数的间断点，可以得到函数图像的特点，进而推导出函数的极限、导数等相关概念。

在实际问题中，函数的间断点也常常与物理、经济等领域的现象相联系。

在解析函数的间断点时，需要注意函数的定义域和函数表达式的特点。

有时候，间断点可能是由于定义域的限制导致的，也可能是由于函数表达式的特性造成的。

因此，在分析函数的间断点时，需要全面考虑函数的定义域和函数表达式的特点，以便准确判断函数是否存在间断点，以及间断点的类型。