(精编资料推荐)函数间断点分类及类型

1三、函数的间断点及其分类如果f (x )在x 0 处不连续, 则称点x 0 为函数f (x )的间断点(或不连续点) . Next f (x ) 在x 0处连续的三要素：)(x f (1)在某邻域内有定义；)(0x N )(lim x f xx 0→(2)存在;(3)00lim ()().xxf x f x →=有一条不满足，x 0为f (x )间断点.xy 1sin=f (x )在x =0 附近无限震荡3间断点分类第一类间断点0()f x −及0()f x +均存在00()(),f x f x −+=00()(),f x f x −+≠第二类间断点0()f x −及0()f x +中至少一个不存在若其中有一个为振荡,若其中有一个为,∞称0x 为可去间断点;称0x 为跳跃间断点.称0x 为无穷间断点;称0x 为振荡间断点;⎧⎨⎩⎧⎨⎩……Previous Next4() , () , f x x x F x A x x ≠⎧=⎨=⎩所以，F (x ) 在x 0处连续.此时有lim ()lim ()x x x x F x f x →→=0()A F x ==Previous Next注如果是函数f (x )的可去间断点，构造0x13四、闭区间上连续函数的性质定义函数f (x ) 定义在区间I 上，有称f (x 0) 是函数f (x ) 在区间I 上的最大(小)值.定理(最值定理) 设 f (x ) 在[a , b ]上连续,即12,[,],a b ξξ∃∈都有1()min (),a x b f f x ξ≤≤=2()max ().a x bf f x ξ≤≤=则 f (x ) 在[a , b ] 上必能取到最大(小)值,12()()()f f x f ξξ≤≤Previous Next 00()()(()())f x f x f x f x ≤≥x I∀∈0,x I ∈若[,],x a b ∈对于一切即15定理(有界性定理)则f (x )在[ a , b ] 上有界.Previous Next 定理(介值定理)若f (x ) 在[ a , b ] 上连续, 至少存在一个使 [ , ]a b ξ∈().f ξμ=若f (x ) 在[ a ,b ]上连续,对任意x ∈[ a , b ] 有m ≤f (x ) ≤M .即,,m M ∃最大值M 和最小值m 之间的任何一个值.则它一定能取到即[,],m M μ∀∈18例证明：方程在( 1 , 2 )中有实根.3310x x −+=证设3()31,f x x x =−+则f (x ) 在[ 1, 2]上连续.又f (1) = -1 , f (2) = 3,根据零点定理, (1, 2),ξ∃∈使()0.f ξ=故方程在( 1 , 2 )中有实根.3310x x −+=Previous Next 即3310ξξ−+=19例如果f (x )在[ a , b ]上连续, 且f (a ) < a , f (b ) > b ,证明：在( a , b )内至少存在一点ξ, 使ξξ=)(f 证,)()(x x f x F −=令0,<由零点定理,使),,(b a ∈∃ξ()()0F f ξξξ=−=b b f b F −=)()(,0>.)(ξξ=f 即Previous Next 则F (x ) 在[ a , b ]上连续.()()F a f a a =−而(构造函数)20例如果f (x )在[ 0, 1 ]上连续, 且f (1) > 1,证明：在( 0, 1 )内至少存在一点ξ, 使2()f ξξ−=证2()()1,F x x f x =−令(0)1F 而=−,0<由零点定理,(0,1),ξ使∃∈2()()10,F f ξξξ=−=(1)(1)1F f =−,0>2().f ξξ即−=则F (x )在[ 0, 1 ]上连续,Previous (变形，构造函数)。

第一章第八节函数的连续性定义1.10.)()(00内有定义的某邻域在点设x U x x f 1.函数在一点连续的定义存在；)(lim )1(0x f x x →若)()(lim )2(00x f x f x x =→则称函数.)(0处连续在点x x f 注1°函数在一点连续的等价定义之一设有函数y = f (x ). 当自变量x 从增量概念:0x 变到,0x x ∆+x ∆则称为自变量的增量(或改变量).若相应地函数y 从)(0x f ),(0x x f ∆+变到则称)()(00x f x x f y −∆+=∆为函数的增量(或改变量).定义1.9（函数在一点连续的增量定义）,00→∆→x x x 就是.0)()(0→∆→y x f x f 就是.0lim 0=→y x ∆∆.)()(00内有定义的某邻域在点设x U x x f ⇔处连续在点0)(x x f定理处连续点在函数0)(x x f 处既左连续又右连续点在0)(x x f ⇔).()()(000x f x f x f ==⇔+−例2解⎪⎪⎩⎪⎪⎨⎧≤<−=<≤=.21,2,1,2,10,)(2x x x x x x f 讨论函数在点x = 1处的连续性.由于=−→)(lim 1x f x 21lim x x −→,1==+→)(lim 1x f x )2(lim 1x x −+→,1=1)(lim 1=→x f x ,2)1(=f 所以f (x ) 在点x = 1 处不连续.≠在区间上每一点都连续的函数, 叫做在该区间上连续的函数, 或者说函数在该区间上连续.,),(内连续如果函数在开区间b a 连续函数的图形是一条连续而不间断的曲线.3. 函数在区间上的连续性.],[)(b a C x f ∈记作, 处右连续端点并且在左a x =,处左连续在右端点b x =.],[)(上连续在闭区间则称函数b a x f如果上述三个条件中有一个不满足，则称f (x )在二、函数的间断点及其分类:)(00条件连续必须满足以下三个处在点函数的去心邻域内有定义的在点x x f x ;)()1(0有定义在点x x f ;)(lim )2(0存在x f x x →).()(lim )3(00x f x f x x =→内有定义，的某去心邻域在点设)()(00x U x x f o1. 定义(或间断点).点x 0 处不连续(或间断)，并称点x 0为f (x )的不连续点lim lim 1=+∞=>−∞→+∞→xx xx a a a 时，当lim lim 1=+∞=>−∞→+∞→xx xx a a a 时，当，x x cot ,tan x csc ,sec 结论：三角函数在其定义域内连续.利用极限的四则运算法则可以证明：推论(连续函数的线性运算法则))( )(x g x f 和α和β是常数,)()(x g x f βα+若函数此运算法则对有限个函数成立.在点0x 连续,则函数)( )(x g x f 和的线性组合在点0 x 连续.结论：反三角函数在其定义域内连续.结论：指数函数，对数函数在其定义域内皆连续.1. 函数记号f 与极限记号可以交换次序;意义:变量代换x=.2的理论依据uϕ(.))(特别地，若定理1.17是定理1.16 的特殊情形例9.),0()(内连续在为常数证明：+∞=µµxy 证xx y ln e µµ==内连续，在),0(ln )(+∞==x x u µϕQ 内连续在而),(e )(+∞−∞==uu f y .),0()(内连续在为常数+∞=∴µµx y 可以证明：µx y =对于μ取任何实数,均在其定义域内连续.结论：幂函数在其定义域内连续.结论：一切初等函数在其定义区间内连续.是指包含在定义域内的区间.）端点为单侧连续=])([x f ϕ1,2≤x x 1,2>−−x x.0,0,2,0,2)(连续性处的在讨论函数=⎩⎨⎧<−≥+=x x x x x x f 解)2(lim )(lim 0+=++→→x x f x x 2=)2(lim )(lim 0−=−−→→x x f x x 2−=.0)(处不连续在点故函数=x x f 备用题例2-1)0()0(+−≠f f =+)0(f =−)0(f ∵∴不存在)(lim 0x f x→例2-3解⎪⎩⎪⎨⎧≥+<=,0,,0,)(x x a x e x f x 设函数应当怎样选择a,使得f (x ) 在x =0 处连续.=−)0(f xx e−→0lim ,1==+)0(f )(lim 0x a x ++→,a =,)0(a f =由连续的充要条件)0()0()0(f f f ==+−得a =1.所以当a =1时，f (x )在x =0处连续.。

函数的间断点及其类型
函数的间断点是指在该点处函数的极限不存在或者左右极限
存在但不相等。

间断点可以分为可去间断点、跳跃间断点和无穷间断点三种类型。

1. 可去间断点：在该点处函数的左右极限都存在且相等，但函数在该点处没有定义。

例如，函数 f(x) = x^2在 x=0 处没有定义，但左右极限都为 0，因此 0 是 f(x)的可去间断点。

2. 跳跃间断点：在该点处函数的左右极限都存在，但不相等。

例如，函数 f(x) = x在 x=0 处的左极限为-1，右极限为 1，因此
0 是 f(x)的跳跃间断点。

3. 无穷间断点：在该点处函数的左右极限至少有一个不存在，或者左右极限都存在但等于正无穷或负无穷。

例如，函数 f(x) = 1/x 在 x=0 处的右极限为正无穷，左极限为负无穷，因此 0 是
f(x)的无穷间断点。

判断一个函数的间断点类型，可以通过计算函数在该点处的左右极限来确定。

如果左右极限都存在且相等，则该间断点为可去间断点；如果左右极限不相等，则该间断点为跳跃间断点；如果至少有一个极限不存在，或者两个极限都存在但等于正无穷或负无穷，则该间断点为无穷间断点。

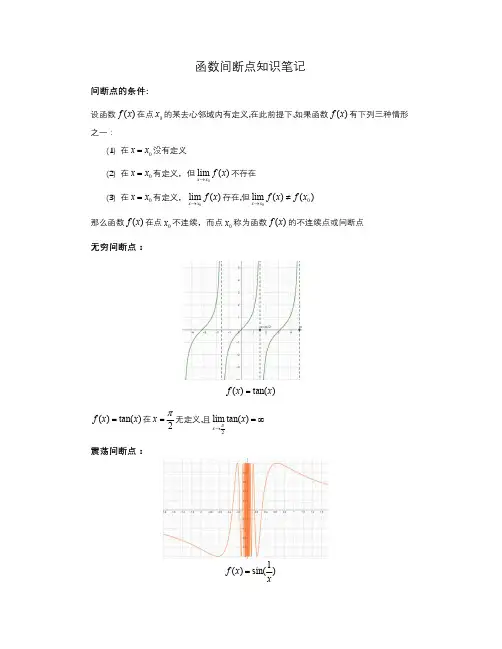
函数间断点知识笔记间断点的条件:设函数()f x 在点0x 的某去心邻域内有定义,在此前提下,如果函数()f x 有下列三种情形之一：(1) 在0x x 没有定义(2) 在0x x 有定义，但0lim ()x x f x 不存在 (3) 在0x x 有定义，0lim ()x x f x 存在,但00lim ()()x x f x f x 那么函数()f x 在点0x 不连续，而点0x 称为函数()f x 的不连续点或间断点无穷间断点：()tan()f x x()tan()f x x 在2x 无定义,且2lim tan()x x 震荡间断点：1()sin()f x x1()sin(f x x在点0x 没有定义,当0x 时，函数值在1 和-1之间变动无限多次 可去间断点：（图不是很好看）21()1x f x x 21()1x f x x 在点1x 没有定义，但在这里有2111lim =lim(1)21x x x x x 如果补充定义:令(1)2f 那么函数在点1x 成为连续，这种情况间断点为可去间断点 同例有函数:,1,()1, 1.2x x f x x ，这里就不论述了. 跳跃间断点：1,0,()0,0,1,0.x x f x x x x当0x 时,0000lim ()lim (1)1lim ()lim (1)1x x x x f x x f x x左右极限都存在但不相等,故0lim ()x f x 不存在,因图像在0x 处产生跳跃现象，该类间断点成为跳跃间断点第一类间断点：左极限0()f x 和0()f x 都存在的间断点（跳跃间断点和可去间断点）第二类间断点：非第一类间断点的所有间断点.(无穷间断点和震荡间断点)。

间断点的定义及分类
函数的间断点是指在该点处函数不连续的点，这些点通常是由于函数在该点处的极限不存在或存在无穷大而引起的。

间断点可以分为以下几类：
- 第一类间断点：在函数在该点处的左右极限都存在的间断点。

- 跳跃间断点：当函数在该点处的左右极限存在但不相等时。

- 可去间断点：当函数在该点处的左右极限相等但该点处的函数值不等于极限值时。

- 第二类间断点：在函数在该点处的左右极限至少有一个不存在的间断点。

- 无限间断点：当函数在该点处的左右极限至少有一个为无穷大时。

- 振荡间断点：当函数在该点处的左右极限存在但不相等且都不为无穷大时。

除了以上提到的两类间断点外，还有一些特殊类型的间断点，例如：垂直间断点、水平间断点和斜间断点等。

这些间断点的存在性和类型可以根据具体函数的性质和定义来判别。

在研究函数的间断点和类型时，通常需要利用极限的思想和方法来进行判断和证明。