下载文档原格式
1三、函数的间断点及其分类如果f (x )在x 0 处不连续, 则称点x 0 为函数f (x )的间断点(或不连续点) . Next f (x ) 在x 0处连续的三要素：)(x f (1)在某邻域内有定义；)(0x N )(lim x f xx 0→(2)存在;(3)00lim ()().xxf x f x →=有一条不满足，x 0为f (x )间断点.xy 1sin=f (x )在x =0 附近无限震荡3间断点分类第一类间断点0()f x −及0()f x +均存在00()(),f x f x −+=00()(),f x f x −+≠第二类间断点0()f x −及0()f x +中至少一个不存在若其中有一个为振荡,若其中有一个为,∞称0x 为可去间断点;称0x 为跳跃间断点.称0x 为无穷间断点;称0x 为振荡间断点;⎧⎨⎩⎧⎨⎩……Previous Next4() , () , f x x x F x A x x ≠⎧=⎨=⎩所以，F (x ) 在x 0处连续.此时有lim ()lim ()x x x x F x f x →→=0()A F x ==Previous Next注如果是函数f (x )的可去间断点，构造0x13四、闭区间上连续函数的性质定义函数f (x ) 定义在区间I 上，有称f (x 0) 是函数f (x ) 在区间I 上的最大(小)值.定理(最值定理) 设 f (x ) 在[a , b ]上连续,即12,[,],a b ξξ∃∈都有1()min (),a x b f f x ξ≤≤=2()max ().a x bf f x ξ≤≤=则 f (x ) 在[a , b ] 上必能取到最大(小)值,12()()()f f x f ξξ≤≤Previous Next 00()()(()())f x f x f x f x ≤≥x I∀∈0,x I ∈若[,],x a b ∈对于一切即15定理(有界性定理)则f (x )在[ a , b ] 上有界.Previous Next 定理(介值定理)若f (x ) 在[ a , b ] 上连续, 至少存在一个使 [ , ]a b ξ∈().f ξμ=若f (x ) 在[ a ,b ]上连续,对任意x ∈[ a , b ] 有m ≤f (x ) ≤M .即,,m M ∃最大值M 和最小值m 之间的任何一个值.则它一定能取到即[,],m M μ∀∈18例证明：方程在( 1 , 2 )中有实根.3310x x −+=证设3()31,f x x x =−+则f (x ) 在[ 1, 2]上连续.又f (1) = -1 , f (2) = 3,根据零点定理, (1, 2),ξ∃∈使()0.f ξ=故方程在( 1 , 2 )中有实根.3310x x −+=Previous Next 即3310ξξ−+=19例如果f (x )在[ a , b ]上连续, 且f (a ) < a , f (b ) > b ,证明：在( a , b )内至少存在一点ξ, 使ξξ=)(f 证,)()(x x f x F −=令0,<由零点定理,使),,(b a ∈∃ξ()()0F f ξξξ=−=b b f b F −=)()(,0>.)(ξξ=f 即Previous Next 则F (x ) 在[ a , b ]上连续.()()F a f a a =−而(构造函数)20例如果f (x )在[ 0, 1 ]上连续, 且f (1) > 1,证明：在( 0, 1 )内至少存在一点ξ, 使2()f ξξ−=证2()()1,F x x f x =−令(0)1F 而=−,0<由零点定理,(0,1),ξ使∃∈2()()10,F f ξξξ=−=(1)(1)1F f =−,0>2().f ξξ即−=则F (x )在[ 0, 1 ]上连续,Previous (变形，构造函数)。
函数间断点类型函数间断点类型是使用数学函数模型表示不同量的研究方法之一。
本类型的断点定义为，在函数的某处存在极端的值，这些值与函数本身没有直接关系，而属于其它值。
它们可以描述一种近似、一种极端、一种变化过程中被钝化或忽略掉的量。
在数学建模中，需要将这些变量写入模式中，以获得准确的结果。
函数间断点常见的有三种类型：无穷断点、有限断点和色系断点。
其中，无穷断点是因函数值趋于无穷而出现的断点，例如函数f（x）=1/x，当x趋向于0时，f（x）将趋向于无穷，因此函数f（x）在x=0处有一个无穷断点。
有限断点是指函数值趋于有限而出现的断点，而色系断点则是指函数值趋于不同色系而出现的断点，函数h（x）=1/(1+x)x=正负无穷处有一个色系断点，它的函数曲线会从蓝变成红。
在实际应用中，函数间断点的研究主要用于解决一些优化问题。
例如，在有限断点的情况下，我们可以计算出此类型的函数的最小值，从而有效地解决相关问题。
另一方面，在无穷断点和色系断点的情况下，可以对函数的参数进行调整，从而使得其满足实际需求。
进行函数间断点研究时，需要结合极大值原理，即函数的极大值或极小值处存在断点。
函数间断点的研究不仅可以用于优化问题，还可以用于预测和解决一些更复杂的问题。
例如，在后现代越来越流行的综合性开发中，断点作为项目的情景转换点，可以用来提供投资最优化、发展最快速和可持续性等特征，从而实现项目的成功开发。
总之，函数间断点类型是一种重要的数学模型，可用于解决各种优化问题、预测问题以及更复杂场景下的综合性问题。
它的研究需要多方面的推理，以找出函数的断点，并利用极大值原理，使其实现最优化。
为了更好地应用函数间断点的研究，我们还需要不断提升认识和实践，以实现最佳效果。
函数的间断点及其类型
函数的间断点是指在该点处函数的极限不存在或者左右极限
存在但不相等。
间断点可以分为可去间断点、跳跃间断点和无穷间断点三种类型。
1. 可去间断点：在该点处函数的左右极限都存在且相等，但函数在该点处没有定义。
例如，函数 f(x) = x^2在 x=0 处没有定义，但左右极限都为 0，因此 0 是 f(x)的可去间断点。
2. 跳跃间断点：在该点处函数的左右极限都存在，但不相等。
例如，函数 f(x) = x在 x=0 处的左极限为-1，右极限为 1，因此
0 是 f(x)的跳跃间断点。
3. 无穷间断点：在该点处函数的左右极限至少有一个不存在，或者左右极限都存在但等于正无穷或负无穷。
例如，函数 f(x) = 1/x 在 x=0 处的右极限为正无穷，左极限为负无穷，因此 0 是
f(x)的无穷间断点。
判断一个函数的间断点类型，可以通过计算函数在该点处的左右极限来确定。
如果左右极限都存在且相等，则该间断点为可去间断点；如果左右极限不相等，则该间断点为跳跃间断点；如果至少有一个极限不存在，或者两个极限都存在但等于正无穷或负无穷，则该间断点为无穷间断点。
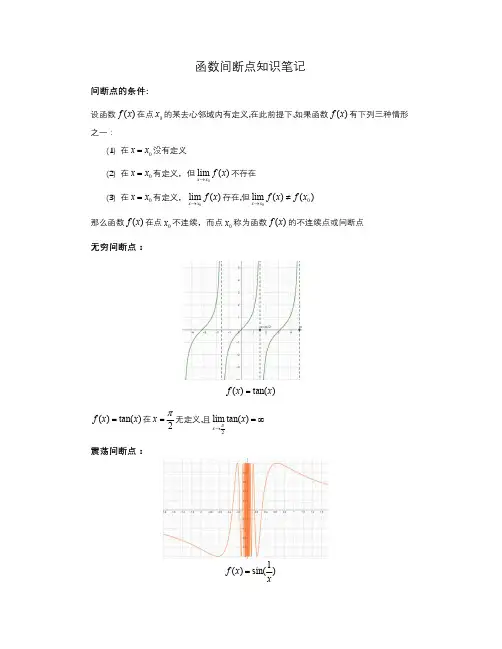
函数间断点知识笔记间断点的条件:设函数()f x 在点0x 的某去心邻域内有定义,在此前提下,如果函数()f x 有下列三种情形之一：(1) 在0x x 没有定义(2) 在0x x 有定义，但0lim ()x x f x 不存在 (3) 在0x x 有定义，0lim ()x x f x 存在,但00lim ()()x x f x f x 那么函数()f x 在点0x 不连续，而点0x 称为函数()f x 的不连续点或间断点无穷间断点：()tan()f x x()tan()f x x 在2x 无定义,且2lim tan()x x 震荡间断点：1()sin()f x x1()sin(f x x在点0x 没有定义,当0x 时，函数值在1 和-1之间变动无限多次 可去间断点：（图不是很好看）21()1x f x x 21()1x f x x 在点1x 没有定义，但在这里有2111lim =lim(1)21x x x x x 如果补充定义:令(1)2f 那么函数在点1x 成为连续，这种情况间断点为可去间断点 同例有函数:,1,()1, 1.2x x f x x ，这里就不论述了. 跳跃间断点：1,0,()0,0,1,0.x x f x x x x当0x 时,0000lim ()lim (1)1lim ()lim (1)1x x x x f x x f x x左右极限都存在但不相等,故0lim ()x f x 不存在,因图像在0x 处产生跳跃现象，该类间断点成为跳跃间断点第一类间断点：左极限0()f x 和0()f x 都存在的间断点（跳跃间断点和可去间断点）第二类间断点：非第一类间断点的所有间断点.(无穷间断点和震荡间断点)。
大一高数知识点总结间断点大一高数知识点总结—间断点高等数学是大一学生必修的一门重要课程，其中的间断点是其中一个重要的知识点。
本文将对间断点的概念、分类和相关性质进行总结和讨论。
一、概念在数学中，我们称函数f(x)在点x=a处存在间断点，当且仅当下面三个条件满足其中之一：1. f(x)在点x=a的左右极限存在，但它们不相等；2. f(x)在点x=a的左右极限存在，但它们等于无穷大；3. f(x)在点x=a的左右极限至少有一个不存在。
二、分类根据间断点的性质，我们可以将间断点分为以下三类：可去间断点、跳跃间断点和无穷间断点。
1. 可去间断点可去间断点也称为可去断点，是指当函数f(x)在点x=a的左右极限存在且相等时，在该点函数值f(a)与左右极限相等的点。
在这种情况下，我们可以通过定义一个新的函数g(x)，使得g(x)在点x=a的左右极限存在且相等，同时g(a)=f(a)，从而在该点解决了间断的问题。
2. 跳跃间断点跳跃间断点是指当函数f(x)在点x=a的左右极限存在，但它们不相等时，函数值f(a)与左右极限存在差距的点。
这种间断点的存在导致函数的图像在相应点上出现明显的跳跃现象。
3. 无穷间断点无穷间断点也称为无穷断点，是指当函数f(x)在点x=a的左右极限存在，且至少一个极限等于正无穷或负无穷时的点。
这种间断点的存在导致函数在相应点上存在发散或趋势以及各种特殊的性质。
三、性质间断点具有以下一些重要的性质，这些性质为我们进一步研究函数的连续性和收敛性提供了基础。
1. 黎曼可积性若函数f(x)在点x=a的左右极限存在且相等，且f(x)在[a,b]上有界，则函数f(x)在区间[a,b]上是黎曼可积的。
2. 连续性若函数f(x)在点x=a的左右极限都存在，且这两个极限等于f(a)，则称f(x)在点x=a连续。
3. 收敛性当函数f(x)在点x=a的左右极限至少有一个不存在，那么我们可以说f(x)在该点的极限不存在或者函数在该点处发散。
函数的连续性与间断点的分类函数是数学中一个十分重要的概念，它描述了输入和输出之间的关系。
在数学分析中，我们常常关注函数的连续性和间断点，它们对于理解函数的性质和行为具有重要的作用。
本文将介绍函数的连续性和间断点的分类，以及它们在数学和实际问题中的应用。
正文：一、函数的连续性函数的连续性是指函数在其定义域内的每个点上都存在极限，并且该极限等于该点处的函数值。
简单来说，函数在其定义域内没有断裂或跳跃的情况，具有连续性。
1.1 间断点的定义函数的间断点是指函数在某个点上不满足连续性的点。
根据间断点的不同性质，可以将其分类为三种类型：可去间断点、跳跃间断点和无穷间断点。
1.2 可去间断点可去间断点是指函数在某一点上不连续，但通过修正或填补可以使其变成一个连续点。
具体来说，如果函数在某一点的左右极限存在且相等，但与该点的函数值不同，则该点为可去间断点。
1.3 跳跃间断点跳跃间断点是指函数在某一点的左右极限存在，但不相等。
换句话说，函数在该点处存在一个有限的跳跃。
跳跃间断点可以通过一个间断点的加法或减法变得连续。
1.4 无穷间断点无穷间断点是指函数在某一点的左右极限至少有一个不存在或为无穷大。
无穷间断点可以分为两类：无穷增长和无穷衰减。
无穷增长的间断点是指函数在某一点的右极限为无穷大，而左极限不存在或为有限。
无穷衰减的间断点则相反，函数在某一点的左极限为无穷小，而右极限不存在或为有限。
二、间断点的应用间断点的概念在数学和实际问题中都具有广泛的应用。
下面将介绍几个常见的应用场景。
2.1 极限的计算在求解函数的极限时，间断点的分析和处理是十分重要的。
根据间断点的类型，我们可以使用不同的方法来计算函数的极限值。
对于可去间断点，通过修正或填补可以消除其影响，从而得到准确的极限值。
而对于跳跃间断点和无穷间断点，我们可以使用极限的性质和定理来计算。
2.2 曲线的绘制在绘制函数的曲线图时，间断点的位置对于曲线的形状和走势有着很大的影响。
从定义出发首先，考察间断点的概念：若y=f(x)再 x=x_{0} 处出现如下三种情况之一，则称 x_{0} 为 y=f(x) 的间断点:(1)y=f(x)在点 x_{0} 处无定义(2)y=f(x)在点x_{0} 处有定义，但 \lim_{x \rightarrow x_{0}}{f(x)} 不存在(3)y=f(x)在点x_{0} 处有定义，但 \lim_{x \rightarrow x_{0}}{f(x)} 存在，但 \ lim_{x\rightarrow x_{0}}{f(x)}≠f(x)据此，我们可以对间断点进行分类第一类间断点第一类间断点也叫有限型间断点，其特点是左右极限均存在.可去间断点可去间断点，据名可知，函数在该处定义极限为函数值，即可将该间断点去除。
即：左极限，右极限存在且相等，但不等于该点的函数值或在该点无定义。
数学语言表示为\lim_{x \rightarrow x_{0}^{-}}{f(x)}=\lim_{x \rightarrowx_{0}^{+}}{f(x)}≠{f(x)}跳跃间断点跳跃间断点，顾名思义，即函数在该间断点两侧像是从一个点跳跃到另一个点。
其判断方法为：左极限和右极限均存在，但不相等。
\lim_{x \rightarrow x_{0}^{-}}{f(x)}≠\lim_{x \rightarrow x_{0}^{+}}{f(x)}第二类间断点第二类间断点左右极限至少有一个不存在。
注：除了第一类间断点其余均为第二类间断点。
无穷间断点在该点可以无定义，且左右极限至少有一个不存在，且改函数在该点极限为∞。
震荡间断点在该点可以无定义，当自变量趋于该点时，函数值再两个常数之间变动无限多次。
此时左右极限均不存在。
另外，值得说明的是，第一类间断点也叫非无穷间断点，平时做题中，除了第一类间断点，其余书写时均判定位第二类间断点。
同时，根据间断点的类型，我们可对判断间断点的题型作处如下总结：step1：找出函数无定义的点。
