基本割集找法

找基本割集的简单方法一、背景介绍基本割集是图论中的一个重要概念，它是指在一个连通图中，删去某个边或节点后使得原来的图不再连通的最小集合。

找到基本割集可以帮助我们更好地理解图的结构和性质，因此在实际应用中具有广泛的应用价值。

二、定义及性质1. 定义：在一个连通图G=(V,E)中，如果删去某个边或节点后使得原来的图不再连通，则这个边或节点被称为该图的割点或割边；如果这个割点或割边所组成的集合是该图不同联通分量之间唯一的，则称这个集合为该图的基本割集。

2. 性质：（1）每个基本割集都至少包含一个割点或者一条割边；（2）对于任意两个不同联通分量之间只有唯一一条路径；（3）将任意一个基本割集划分成两部分，则这两部分所对应的子图均为联通图。

三、找基本割集方法1. 基于DFS算法深度优先搜索算法（DFS）可以遍历整张连通图，并根据遍历顺序来确定每个节点的遍历顺序。

在DFS遍历的过程中，如果我们发现某个节点的子节点不再与该节点相连，则说明该节点是一个割点，而该节点所连接的两个子图就是一个基本割集。

具体步骤如下：（1）从任意一个节点开始进行DFS遍历；（2）记录每个节点的遍历顺序和最早访问时间；（3）对于每个非根节点v，如果存在一个子节点w，满足dfn[w]<low[v]，则说明v是一个割点；（4）对于每个连通分量，将其所有割点和相应子图组成的集合作为一个基本割集。

2. 基于BFS算法广度优先搜索算法（BFS）也可以用来找到基本割集。

具体步骤如下：（1）从任意一个节点开始进行BFS遍历；（2）记录每个节点的层数和最早访问时间；（3）对于每个非根节点v，如果存在一个子节点w且dfn[w]>=depth[v]，则说明v是一个割点；（4）对于每个连通分量，将其所有割点和相应子图组成的集合作为一个基本割集。

3. 基于Tarjan算法Tarjan算法是一种高效的寻找强连通分量的算法，在寻找强连通分量的过程中可以顺带找到基本割集。

第9章 习题解答9.1 有5片树叶.分析 设T 有x 个1度顶点(即树叶).则T 的顶点数Tx x n ,523+=++=的边数.41x n m +=-=由握手定理得方程.∑=+=⋅+⨯+⨯==+=ni ix x vd x m 1.1312233)()4(22由方程解出.5=x所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.分析 设T 中有x 个3度顶点,则T 中的顶点数,7x n +=边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122由方程解出x=5.所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.要析 设T 中有x 个3度顶点,则T 中的顶点数x n +=7,边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122.由此解出5=x ,即T 中有5个3度顶.T 的度数列为1,1,1,1,1,1,1,3,3,3,3,3.由于T 中只有树叶和3度顶点,因而3度顶点可依次相邻,见图9.7所示. 还有一棵与它非同构的树,请读者自己画出.9.3 加1-k 条新边才能使所得图为无向树.分析 设具有k 个连通分支的森林为G,则G 有k 个连通分支i K T T TT ,,,21全为树,.,,2,1k i =加新边不能在i T 内部加,否则必产生回路.因而必须在不同的小树之间加新边. 每加一条新边后,所得到的森林就减少一个连通分支. 恰好加1-k 条新边,就使得图连通且无回路,因而是树.在加边过程中,只需注意,不在同一人连通分支中加边. 下面给出一种加边方法,取iv 为iT 中顶点,加新边1,,2,1),(1-=+k i vv i i,则所得图为树,见图9.8 给出的一个特例.图中虚线边为新加的边.9.4 不一定.分析 n 阶无向树T 具有1-n 条边,这是无向树T 的必要条件,但不是充公条件.例如, 阶圈(即1-n 个顶点的初级回路)和一个孤立点组成无向简单图具有1-n 条边, 但它显然不是树.9.5 非同构的无向树共有2棵,如图 9.9所示.分析由度数列1,1,1,1,2,2,4不难看出，唯一的4度顶点必须与2度顶点相邻，它与1个2度顶点相邻，还是与两个2度顶点都相邻，所得树是非同构的，再没有其他情况.因而是两棵非同构的树.9.6 有两棵非同构的生成树,见图9.10所示.分析图9.10 是5阶图(5个顶点的图), 5阶非同构的无向树只有3棵,理由如下. 5阶无向树中,顶点数5=n,边数4=m,各顶点度数之和为8,度数分配方案有3种,分别为①1,1,1,1,4;②1,1,1,2,3;③1,1,2,2.2.每种方案只有一棵非同构的树.图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种,也就是说,它至多有3棵非同构的生成树, 但由于图中无4度顶点,所示,不可能有度数列为①的生成树,于是该图最多有两棵非同构的生成树. 但在图9.10 中已经找出了两个非同构的生成树,其中(1)的度数列为③,(2) 的度数列为②,因而该图准确地有两棵非同构的生成树.9.7 基本回路为: .,,,hfab C gfa C ead C cbad C h g e c====基本回路系统为}.,,,{h g e cC C C C基本割集为:},,{},,{},,,{},,,,,{h g f Sc ed S h c b S h g ce a S fd b a ====基本回路系统为},,,{f d b aS S S S.分析 1°注意基本回路用边的序列表示,而基本割集用边的集合表示.2° 基本回路中,只含一条弦,其余的边全为树枝,其求法是这样的: 设弦),(j iv ve =,则jiv v,在生成树T 中,且在T 中,ji v v ,之间存在唯一的路径ji ,Γ与),(j iv ve =组成的回路为G 中对应弦e 的基本回路.3° 基本割集中,只含一条树枝,其余的边都是弦,其求法是这样的:设树枝),(j iv ve =,则e 为T 中桥,于是eT-(将e 从T中支掉),产生两棵小树1T 和2T ,则}|{21'''中和的两端点分别在中且在T T e G e e S e =e S 为树枝e 对应的基本割集. 显然ee S S e ,∈中另外的边全是弦. 注意,两棵小树1T 和2T ,中很可能有平凡的树(一个顶点).aT -得两棵小树如图9.11中(1) 所示. G 中一个端点在i T 中,另一个端点在2T 中的边为a(树枝), h g c e ,,,,它们全是弦,于是},,,,{h g c e a Sa=bT - 得两棵小树如图9.11中(2) 所示, 其中有一棵为平凡树. G 中一个端点在1T 中,另一个端点在2T 中的边数除树枝b 外,还有弦,,h c 所以, },,{h c b Sb=dT -产生的两棵小树如图9.11中(3) 所示 . G 中一个端点在1T 中,另中一个端点在2T 中的边,除树枝d 外,还有两条弦e c ,,所示, },,{e c d Sd=fT -产生的两棵小树如图9.11中(4) 所示. 由它产生的基本割集为},,{h g f Sf=9.8 按Kruskal 求最小生成树的算法,求出的图9.3(1)的最小生成树T 为图9.12中(1) 所示, 其7)(=T W .(2) 的最小生成树T 为图9.12中(2)所示,其.11)(=T W9.9 421,,B B B为前缀码.分析 在421,,B B B中任何符号串都不是另外符号串的前串,因而它们都是前缀码.而在3B 中, 1是11,101的前缀,因而3B不是前缀码. 在5B 中,,a 是ac aa ,等的前缀,因而5B 也不是前缀码.9.10 由图9.4 (1) 给出的2元前缀码.}11,011,01010,0100,00{1=B由(2) 给出的3元前缀码为.}.2,1,022,0202,0201,0200,01,00{2=B分析 1B 是2元树产生的2元前缀码(因为码中的符号串由两个符号0,1组成),类似地,2B 是由3元树产生的3元前缀码(因为码中符号串由3个符号0,1,2组成).一般地,由r 元树产生r 元前缀码.9.11 (1) 算式的表达式为ji h g f e d c b a *)*()()*)*((((++÷-+.由于使其成为因而可以省去一些括号优先于,,,*,-+÷ji h g f e d c b a **)()*)*((++÷-+.(2) 算式的波兰符号法表达式为.****hij fg bcde a ++-÷+(3) 算式的逆波兰符号法表达式为.****+÷+-+jI hi fg e d abc9.12 答案 A:①; B ②; C:④; D:⑨.分析 对于每种情况都先求出非同构的无向树,然后求出每棵非同构的无向树派生出来的所有非同构的根树.图9.13 中,(1),(2),(3),(4)分别画出了2阶,3阶,4阶,5阶所有非同构的无向树,分别为1棵,1棵,2棵和3棵无向树.2阶无向树只有1棵,它有两个1度顶点,见图9.13中(1)所示,以1个顶点为树根,1个顶点为树叶,得到1棵根树.3阶非同的无向树也只有1棵,见图9.13中(2)所示.它有两个1度顶点,1个2度顶点,以1度顶点为根的根树与以2度顶点为根的树显然是非同构的根树,所以2个阶非同构的根树有两棵.4阶非同构的无向树有两棵,见图9.13中(3)所示. 第一棵树有3片树叶,1个3度顶点, 以树叶为根的根树与以3度顶点为根的树非同构.所以,由第一棵树能生成两个非同构的根树, 见图9.14 中(1)所示. 第二棵树有两片树叶,两个2度顶点,由对称性,以树叶为根的根树与2度顶点为根的根树非同构,见图9.14中(2) 所示. 所以,4阶非同构的根树有4棵.5阶非同构的无向树有3棵,见图9.13中(4)所示. 由第一棵能派生两棵非同构的根树, 由第二棵能派生4棵非同构的根树,由第三棵能派生3棵非同构的根树,所以,5阶非同构的根树共有9棵,请读者将它们都画出来.9.13 答案 A:②; B:②; C:③; D:③; E:③;F:④; G: ④; H:③.分析 将所有频率都乘100,所得结果按从小到大顺序排列:.35,20,15,10,10,5,5=======a b c d e f g w w w w w w w以以上各数为权,用Huffman 算法求一棵最优树,见图9.15所示.对照各个权可知各字母的前缀码如下:a ——10，b ——01，c ——111，d ——110，e ——001，f ——0001，g ——0000.于是，a,b 的码长为e d c ,,,2的码长为g f ,,3的码长为4. W(T)=255(各分支点的权之和),W(T)是传输100按给定频率出现的字母所用的二进制数字,因则传输104个按上述频率出现的字母要用25500⨯个二进制数字..24=1055最后还应指出一点,在画最优树叶, 由于顶点位置的不同,所得缀码可能不同,即有些字母的码子在不同的最优树中可能不同,但一般说来码长不改变.特别是,不同的最优树,它们的权是固定不变的.9.14 答案 A:②; B:④分析用2元有序正则树表示算式,树叶表示参加运算的数,分支点上放运算符,并将被减数(被除数)放在左子树上,所得2元树如图9.16所示.用前序行遍法访问此树,得波兰符号表示法为abc-++de-*.**ghf用后序行遍法访问此树,得逆波兰符号表示法为dec*fghab--++**。

危害、危险辨识与评价之————危险性分析评价法之——事故树分析一、事故树分析（FTA）－定性分析事故树定性分析就是对事故树中各事件不考虑发生概率多少，只考虑发生和不发生两种情况。

通过定性分析可以知道哪一个或哪几个基本事件发生，顶上事件就一定发生，哪一个事件发生对顶上事件影响大，哪一个影响少，从而可以采取经济有效的措施，防止事故发生。

事故树定性一分析包括求最小割集和最小径集，计算各基本事件的结构重要度，在此基础上确定安全防灾对策。

（1）最小割集和最小径集在事故树中，如果所有的基本事件都发生则顶上事件必然发生。

但是在很多情况下并非如此，往往是只要某个或几个事件发生顶上事件就能发生。

凡是能导致顶上事件发生的基本事件的集合就叫割集。

割集也就是系统发生故障的模式。

在一棵事故树中，割集数目可能有很多，而在内容上可能有相互包含和重复的情况，甚至有多余的事件出现，必须把它们除去，除去这些事件的割集叫最小割集。

也就是说凡能导致顶上事件发生的最低限度的基本事件的集合称为最小割集。

在最小割集里，任意去掉一个基本事件就不成其为割集。

在事故树中，有一个最小割集，顶上事件发生的可能性就有一种。

事故树中最小割集越多，顶上事件发生的可能性就越多，系统就越危险。

相反地，在事故树中，有一组基本事件不发生，顶上事件就不发生，这一组基本事件的集合叫径集。

径集是表示系统不发生故障而正常运行的模式。

同样在径集中也存在相互包含和重复事件的情况，去掉这些事件的径集叫最小径集。

也就是说，凡是不能导致顶上事件发生的最低限度的基本事件的集合叫最小径集。

在最小径集中，任意去掉一个事件也不成其径集。

事故树有一个最小径集，顶上事件不发生的可能性就有一种。

最小径集越多，顶上事件不发生的途径就越多，系统也就越安全。

上述所谓的集合，就是满足某种条件或具有某种属性的事物的全体。

集合的每一个成员称为这个集合的元素。

例如一个班级全体学生构成了一个集合，一个车队的全部汽车也构成一个集合。

第九章网络图论基础9．2．1 网络图论的基本概念(1)图：由“点(节点)”和“线(支路)”组成的图形称为图，通常用符号G 来表示。

(2)子图：图的一部分(允许孤立的节点，不允许孤立的支路)。

(3)有向图：若图G的每条支路都标有一个方向，则称为有向图，否则称为无向图。

(4)连通图：若图中的任意两个节点之间均至少存在一条由支路构成的路径，则称为连通图，否则称为非连通图，孤立的节点也是连通图。

(5)数、树枝、连枝：不包含回路，但包含图的所有节点的连通的子图为树；组成树的支路为树枝；其余支路为连枝。

(6)回路：从图中某一节点出发，经过若干支路和节点(均只许经过一次)又回到出发节点所形成的闭合路径称为回路。

(7)基本回路：只含一个连枝的回路，也称单连枝回路。

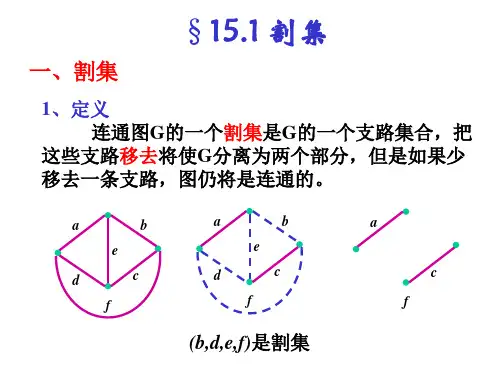
(8)割集：割集是一组支路的集合，如果把这些支路全部移走(保留支路的两个端点)，则此图变成两个分离的部分，而少移去任一条支路，图仍是连通的。

(9)基本割集：只含一个树枝的割集，也称单树枝割集。

9．2．2 图的矩阵表示图的支路与节点、支路与回路、支路与割集的关联性质均可以用相应的矩阵来描述。

一、关联矩阵A关联矩阵A又称为节点支路关联矩阵，它反映的是节点与支路的关联情况。

设一有向图的节点数为n，支路数为b，则节点与支路的关联情况可以用一个n×b的矩阵来表示，记为Aa ，称为图的增广关联矩阵，Aa的每一行对应一个节点，每一列对应一个支路，其第i行第j列的元素aij定义为：由于Aa 的行不是彼此独立的，即Aa中的任一行都能从其他(n-1)行导出，因此，若由矩阵Aa中任意划出一行，剩下的(n-1)×b阶矩阵称为降阶关联矩阵，用A表示，又称为关联矩阵。

被划去的一行所对应的节点可当作参考节点。

二、回路矩阵B对于任一个具有n个节点，b条支路、c个回路的有向图，回路与支路的关联情况可以用一个(c×b)阶矩阵来描述，记为Ba ，Ba的每一行对应一个回路，每一列对应一个支路，其第i行第j列的元素bij定义为：若从矩阵Ba中取出独立回路所组成的(b-n+1)×b阶矩阵称为独立回路矩阵，简称回路矩阵。

第9章习题解答9.1 有5片树叶.分析设T有x个1度顶点(即树叶).则T的顶点数的边数由握手定理得方程.由方程解出所求无向树T的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T中有5个3度顶点.分析设T中有个3度顶点,则T中的顶点数边数,由握手定理得方程.由方程解出x=5.所求无向树T的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T中有5个3度顶点.要析设T中有x个3度顶点,则T中的顶点数,边数,由握手定理得方程..由此解出,即T中有5个3度顶.T的度数列为1,1,1,1,1,1,1,3,3,3,3,3.由于T中只有树叶和3度顶点,因而3度顶点可依次相邻,见图9.7所示. 还有一棵与它非同构的树,请读者自己画出.9.3 加条新边才能使所得图为无向树.分析设具有个连通分支的森林为G,则G有个连通分支全为树,加新边不能在内部加,否则必产生回路.因而必须在不同的小树之间加新边. 每加一条新边后,所得到的森林就减少一个连通分支. 恰好加条新边,就使得图连通且无回路,因而是树.在加边过程中,只需注意,不在同一人连通分支中加边. 下面给出一种加边方法,取为中顶点,加新边,则所得图为树,见图9.8 给出的一个特例.图中虚线边为新加的边.9.4 不一定.分析 n阶无向树T具有条边,这是无向树T的必要条件,但不是充公条件.例如, 阶圈(即个顶点的初级回路)和一个孤立点组成无向简单图具有条边, 但它显然不是树.9.5 非同构的无向树共有2棵,如图 9.9所示.分析由度数列1,1,1,1,2,2,4不难看出，唯一的4度顶点必须与2度顶点相邻，它与1个2度顶点相邻，还是与两个2度顶点都相邻，所得树是非同构的，再没有其他情况.因而是两棵非同构的树.9.6 有两棵非同构的生成树,见图9.10所示.分析图9.10 是5阶图(5个顶点的图), 5阶非同构的无向树只有3棵,理由如下. 5阶无向树中,顶点数,边数,各顶点度数之和为8,度数分配方案有3种,分别为①1,1,1,1,4;②1,1,1,2,3;③1,1,2,2.2.每种方案只有一棵非同构的树.图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种,也就是说,它至多有3棵非同构的生成树, 但由于图中无4度顶点,所示,不可能有度数列为①的生成树,于是该图最多有两棵非同构的生成树. 但在图9.10 中已经找出了两个非同构的生成树,其中(1)的度数列为③,(2) 的度数列为②,因而该图准确地有两棵非同构的生成树.9.7 基本回路为:基本回路系统为基本割集为:基本回路系统为.分析1°注意基本回路用边的序列表示,而基本割集用边的集合表示.2° 基本回路中,只含一条弦,其余的边全为树枝,其求法是这样的: 设弦,则在生成树T中,且在T中,之间存在唯一的路径与组成的回路为G中对应弦的基本回路.3° 基本割集中,只含一条树枝,其余的边都是弦,其求法是这样的:设树枝,则为T中桥,于是(将从T中支掉),产生两棵小树和,则为树枝对应的基本割集. 显然中另外的边全是弦. 注意,两棵小树和,中很可能有平凡的树(一个顶点).得两棵小树如图9.11中(1) 所示. G中一个端点在中,另一个端点在中的边为(树枝),,它们全是弦,于是得两棵小树如图9.11中(2) 所示, 其中有一棵为平凡树. G中一个端点在中,另一个端点在中的边数除树枝外,还有弦所以,产生的两棵小树如图9.11中(3) 所示 . G中一个端点在中,另中一个端点在中的边,除树枝外,还有两条弦,所示,产生的两棵小树如图9.11中(4) 所示. 由它产生的基本割集为.9.8 按Kruskal求最小生成树的算法,求出的图9.3(1)的最小生成树T为图9.12中(1) 所示, 其.(2) 的最小生成树T为图9.12中(2)所示,其9.9为前缀码.分析在中任何符号串都不是另外符号串的前串,因而它们都是前缀码.而在中, 1是11,101的前缀,因而不是前缀码. 在中,是等的前缀,因而也不是前缀码.9.10 由图9.4 (1) 给出的2元前缀码.由(2) 给出的3元前缀码为.分析是2元树产生的2元前缀码(因为码中的符号串由两个符号0,1组成),类似地,是由3元树产生的3元前缀码(因为码中符号串由3个符号0,1,2组成).一般地,由元树产生元前缀码.9.11 (1) 算式的表达式为.由于.(2) 算式的波兰符号法表达式为(3) 算式的逆波兰符号法表达式为9.12 答案A:①; B②; C:④; D:⑨.分析对于每种情况都先求出非同构的无向树,然后求出每棵非同构的无向树派生出来的所有非同构的根树.图9.13 中,(1),(2),(3),(4)分别画出了2阶,3阶,4阶,5阶所有非同构的无向树,分别为1棵,1棵,2棵和3棵无向树.2阶无向树只有1棵,它有两个1度顶点,见图9.13中(1)所示,以1个顶点为树根,1个顶点为树叶,得到1棵根树.3阶非同的无向树也只有1棵,见图9.13中(2)所示.它有两个1度顶点,1个2度顶点,以1度顶点为根的根树与以2度顶点为根的树显然是非同构的根树,所以2个阶非同构的根树有两棵.4阶非同构的无向树有两棵,见图9.13中(3)所示. 第一棵树有3片树叶,1个3度顶点, 以树叶为根的根树与以3度顶点为根的树非同构.所以,由第一棵树能生成两个非同构的根树, 见图9.14 中(1)所示. 第二棵树有两片树叶,两个2度顶点,由对称性,以树叶为根的根树与2度顶点为根的根树非同构,见图9.14中(2) 所示. 所以,4阶非同构的根树有4棵.5阶非同构的无向树有3棵,见图9.13中(4)所示. 由第一棵能派生两棵非同构的根树, 由第二棵能派生4棵非同构的根树,由第三棵能派生3棵非同构的根树,所以,5阶非同构的根树共有9棵,请读者将它们都画出来.9.13 答案A:②; B:②; C:③; D:③; E:③;F:④; G: ④; H:③.分析将所有频率都乘100,所得结果按从小到大顺序排列:以以上各数为权,用Huffman算法求一棵最优树,见图9.15所示.对照各个权可知各字母的前缀码如下:a——10， b——01， c——111， d——110，e——001， f——0001，g——0000.于是，a,b的码长为的码长为的码长为4.W(T)=255(各分支点的权之和),W(T)是传输100按给定频率出现的字母所用的二进制数字,因则传输104个按上述频率出现的字母要用个二进制数字.最后还应指出一点,在画最优树叶, 由于顶点位置的不同,所得缀码可能不同,即有些字母的码子在不同的最优树中可能不同,但一般说来码长不改变.特别是,不同的最优树,它们的权是固定不变的.9.14 答案 A:②; B:④分析用2元有序正则树表示算式,树叶表示参加运算的数,分支点上放运算符,并将被减数(被除数)放在左子树上,所得2元树如图9.16所示.用前序行遍法访问此树,得波兰符号表示法为用后序行遍法访问此树,得逆波兰符号表示法为。