割集分析法工科
- 格式:doc
- 大小:175.00 KB
- 文档页数:9





最小割集求法相关概念求解方法(行列法结构法布尔代数化简法)相关概念割集——也叫做截集或截止集,它是导致顶上事件发生的基本事件的集合。
也就是说事故树中一组基本事件的发生,能够造成顶上事件发生,这组基本事件就叫割集。
引起顶上事件发生的基本事件的最低限度的集合叫最小割集。
径集——也叫通集或导通集,即如果事故树中某些基本事件不发生,顶上事件就不发生。
那么,这些基本事件的集合称为径集。
不引起顶上事件发生的最低限度的基本事件的集合叫最小径集。
TOP求解方法行列法结构法布尔代数化简法行列法行列法是1972年福塞尔提出的方法,所以也称其为福塞尔法。
其理论依据是:“与门”使割集容量增加,而不增加割集的数量;“或门”使割集的数量增加,而不增加割集的容量。
这种方法是从顶上事件开始,用下一层事件代替上一层事件,把“与门”连接的事件,按行横向排列;把“或门”连接的事件,按列纵横向摆开。
这样,逐层向下,直至各基本事件,列出若干行,最后利用布尔代数化简。
化简结果,就得出若干最小割集。
为了说明这种计算方法,我们以图4—25所示的事故树为例,求其最小割集。
事故树示意图我们看到,顶上事件T与中间事件A1、A2是用“或门”连接的,所以,应当成列摆开,即A1、A2与下一层事件B1、B2、X1、X2、X4的连结均为“与门”,所以成行排列:下面依此类推:整理上式得:下面对这四组集合用布尔代数化简,根据A·A=A,则X1·X1=X1,X4·X4=X4,即又根据A+A·B=A,则X1·X2+X1·X2·X3=X1·X2,即于是,就得到三个最小割集{X1,X2},{ X4,X5},{ X4,X6}。
按最小割集化简后的事故树,如图4-26所示:事故树等效图TOP结构法这种方法的理论根据是:事故树的结构完全可以用最小割集来表示。
下面再来分析图4-25事故树示意图: A 1∪A 2=X 1·B 1·X 2∪X 4·B 2=X 1·(X 1∪X 3)·X 2∪X 4·(C ∪X 6)=X 1·X 2∪X 1·X 3·X 2∪X 4·(X 4·X 5∪X 6) =X 1·X 2∪X 1·X 2·X 3∪X 4·X 4·X 5∪X 4·X 6 =X 1·X 2∪X 1·X 2·X 3∪X 4·X 5∪X 4·X 6 =X 1·X 2∪X 4·X 5∪X 4·X 6这样,得到的三个最小割集{ X 1,X 2}、{X 4,X 5}、{X 4,X 6}完全与上例用行列法得到的结果一致。


电路中割集满足的条件在电路中,割集是指在电路中切断两个或多个节点所需的最少的连线集合。
割集在电路分析和设计中起着重要的作用,它决定了电路的可靠性和性能。
下面将介绍割集满足的条件。
1. 割集是无环的:割集是通过切断节点之间的连线来实现的,因此割集中不能存在环路。
如果存在环路,那么切断其中一个连线就会导致电流无法流通,电路无法正常工作。
2. 割集包含至少一个节点:割集是通过切断节点之间的连线来实现的,因此割集中必须包含至少一个节点。
如果割集中没有节点,那么切断的连线就没有意义,电路仍然可以正常工作。
3. 割集中的连线数最少:割集是通过切断节点之间的连线来实现的,因此割集中的连线数应尽量少。
如果割集中的连线数过多,那么切断这些连线就会导致电路中断的部分过多,电路的可靠性会受到影响。
4. 割集之间没有公共节点:割集是通过切断节点之间的连线来实现的,因此割集之间不能有公共的节点。
如果割集之间有公共的节点,那么切断一个割集中的连线就会同时影响其他割集,导致电路无法正常工作。
5. 割集覆盖所有节点:割集是通过切断节点之间的连线来实现的,因此割集应覆盖电路中的所有节点。
如果存在没有被割集覆盖的节点,那么切断其他连线也无法切断这些节点之间的连线。
6. 割集之间没有公共连线:割集是通过切断节点之间的连线来实现的,因此割集之间不能有公共的连线。
如果割集之间有公共的连线,那么切断一个割集中的连线就会同时影响其他割集,导致电路无法正常工作。
7. 割集覆盖所有连线:割集是通过切断节点之间的连线来实现的,因此割集应覆盖电路中的所有连线。
如果存在没有被割集覆盖的连线,那么切断其他连线也无法切断这些连线。
电路中割集满足的条件包括割集是无环的、割集包含至少一个节点、割集中的连线数最少、割集之间没有公共节点、割集覆盖所有节点、割集之间没有公共连线以及割集覆盖所有连线。
这些条件保证了割集在电路中的有效性和可靠性,对于电路的分析和设计具有重要的意义。


图论中的割集算法设计与分析在图论中,割集(Cut Set)是指将图的顶点集合分成两个不相交的子集,使得其中一个子集与剩余部分构成一个切割。
割集算法是一种用于寻找割集的方法,它在诸多领域中都有广泛的应用。
本文将对割集算法的设计与分析进行探讨。
一、割集算法的概述割集算法的目标是寻找图中的最小割集,即将图划分成两个子图,并且割集中的边数最少。
最常用的割集算法是基于图的最大流最小割定理的Ford-Fulkerson算法。
该算法通过不断增加流量来找到切割,直到无法再增加为止。
然而,该算法在实践中的效率并不高,因此人们提出了许多改进的割集算法。
二、割集算法的设计1. Stoer-Wagner算法Stoer-Wagner算法是一种启发式算法,它通过迭代地计算图的最小割来找到割集。
该算法的基本思想是将图中的所有顶点分为两个集合,然后计算两个集合之间的最小割。
重复此过程,每次都将最小割的集合合并,直到只剩下一个顶点为止。
最后得到的割集即为图的最小割集。
2. Kernighan-Lin算法Kernighan-Lin算法是一种以贪心策略为基础的割集算法。
该算法的主要思想是通过不断地交换顶点,使得交换后的两个子图之间的割集权重最小。
算法的具体步骤如下:(1)初始时,将图的顶点随机分为两个子集。
(2)计算两个子集之间的割集权重。
(3)选择两个子集中的一个顶点v,将其从一个子集中移动到另一个子集中,并计算割集权重的变化量。
(4)重复步骤(3),直到无法得到更优的割集权重为止。
三、割集算法的分析1. 时间复杂度割集算法的时间复杂度与算法的设计有关。
对于Ford-Fulkerson算法,其时间复杂度为O(E * F),其中E是图中的边数,F是最大流的值。
而对于启发式算法如Stoer-Wagner算法和Kernighan-Lin算法,其时间复杂度通常为O(V^3)或O(V^4),其中V是图中的顶点数。
2. 空间复杂度割集算法的空间复杂度主要取决于图的表示方法。

故障树最小割集Company number:【0089WT-8898YT-W8CCB-BUUT-202108】故障树定性分析—最小割集及其求法故障树分析,包括定性分析和定量分析两种方法。
在定性分析中,主要包括最小割集、最小径集和重要度分析。
限于篇幅,以下仅介绍定性分析中的最小割集和最小径集。
最小割集及其求法割集:它是导致顶上事件发生的基本事件的集合。
最小割集就是引起顶上事件发生必须的最低限度的割集。
最小割集的求取方法有行列式法、布尔代数法等。
现在,已有计算机软件求取最小割集和最小径集。
以下简要介绍布尔代数化简法。
图8-9为一故障树图,以下是用布尔代数化简的过程。
图8-9 故障树T=A1+A2=X1 X2 A3+X4 A4=X1 X2 (X1+X3)+ X4 (X5+X6)=X1 X2 A1+X1 X2 A3+ X4 X5+X4 X6=X1 X2+ X4 X5+X4 X6所以最小割集为{X1,X2},{X4,X5},{X4,X6}。
结果得到三个交集的并集,这三个交集就是三个最小割集E1={X1,X2},E2={X4,X5},E3={X4,X6}。
用最小割集表示故障树的等效图如图8-10。
故障树定性分析—最小割集和最小径集在故障树分析中的应用(1)最小割集表示系统的危险性求出最小割集可以掌握事故发生的各种可能,了解系统的危险性。
每个最小割集都是顶上事件发生的一种可能,有几个最小割集,顶上事件的发生就有几种可能,最小割集越多,系统越危险。
从最小割集能直观地、概略地看出,哪些事件发生最危险,哪些稍次,哪些可以忽略,以及如何采取措施,使事故发生概率下降。
例:共有三个最小割集{X1} 、{X2,X3} 、{X4,X5,X6,X7 ,X8},如果各基本事件的发生概率都近似相等的话,一般地说,一个事件的割集比两个事件的割集容易发生,五事件割集发生的概率更小,完全可以忽略。
因此,为了提高系统的安全性,可采取技术、管理措施以便使少事件割集增加基本事件。
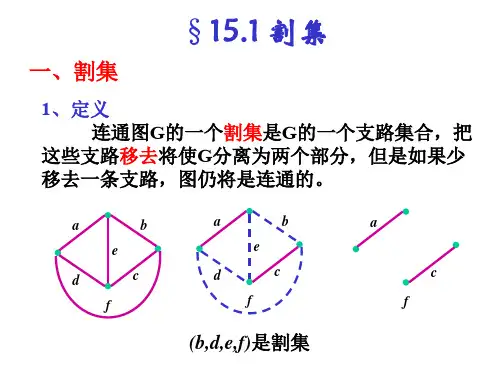
§3-6 割 集 分 析 法
一、割集与基本割集
1)、割集 割集是支路的集合,它必须满足以下两个条件: (1) 移去该集合中的所有支路,则图被分为两部分。
(2) 当少移去该集合中的任何一条支路,则图仍是连通的。
需要说明的是,在移去支路时,与其相连的结点并不移去。
图G 是一个连通图,如图3-26(a)所示,支路集合{1,5,2}、{1,5,3,6}、{2,5,4,6}均为图G 割集。
将以上割集的支路用虚线表示,分别如图3-26(b)、(c)、(d)所示,不难看出,去掉虚线支路后,各图均被分成了两部分,但是
图3-26 图G 及其割集
(a)
(b)
(c)
(d)
只要少去掉其中的一条虚线支路,图仍然是连通的,故满足割集所要求的条件。
而支路集合{1,5,4,6}、{1,2,3,4,5}不是图G 的割集。
将集合中的支路用虚线表示后如图3-27(a)和(b)所示。
对于图3-27(a)来说,移去支路1、5、4、6后,图虽说被分为两部分(结点①为其中的一部分),但如不移去支路5,图仍被分为两部分;而对于图3-27(b)来说,将支路1、2、3、4、5移去后,图则被分成了三部分,故以上两种支路集合不是割集。
2)、作高斯面确定割集
在图G 上作一个高斯面(闭合面),使其包围G 的某些节点,而每条支路只能被闭合面切割一次,去掉与闭合面相切割的支路,图G 将被分为两部分,那么这组支路集合即为图G 的一个割集。
在图G 上画高斯面(闭合面)C 1、C 2、
(a)
(b)
图3-27 非割集说明
①
②
①
②
C 3如图3-28所示,对应割集C 1、C 2、C 3的支路集合为{1,5,2}、{1,5,3,6}、{2,5,4,6}。
3)、基本割集
基本割集又称单树支割集,即割集中只含一条树支,其余均为连支。
如选支路1、5、3为树支,如图3-29所示,则割集C 1,C 2,C 3为基本割集,基本割集的方向与树支的参考方向一致。
当树选定后,对应的基本割集是唯一确定的。
当然选的树不同,相应的基本割集也就不同。
如选支路1、5、6为树支以及选支路1、5、2为树支的基本割集分别如图3-30 (a)和(b)所示。
当图G 有n 个结点、b 条支路时,基本割集的数目等于树支数,为(n -1)。
图3-28 作高斯面确定割集
C 1
2
C 3
图3-29 基本割集
二、割集分析法
割集分析法与回路分析法一样,是建立在“树”的基础上的一种分析方法。
割集分析法是将树支电压作为一组独立的求解变量,根据基本割集建立KCL 方程,因此割集分析法也可以称为割集电压分析法。
割集分析法的选树原则与回路分析法相同,即尽可能将电压源及电压控制量选为树支,电流源及电流控制量选为连支。
设网络的图有n 个结点,b 条支路,则割集分析法中基本割集的数目与树支数相等,为(n -1)个,树支电压变量也为(n -1)个。
因此当电路中电压源支路较多时,采用割集分析法最为有效。
下面通过例题说明割集分析法的求解过程。
图3-30 基本割集示例 C 1
(b)
(a)
C 3
C 2
例3-16 用割集分析法求图3-34(a )所示电路。
解:割集分析法的求解步骤如下:
(1) 画出电路的拓扑图,选一个“合适”的树,并给各
支路定向。
本电路的拓扑图如图3-34(b )所示。
其中粗线为树,树支电压为u 1、u 2、u 3,参考方向如箭头方向所示。
(2) 画出基本割集及其参考方向。
基本割集C 1、C 2、C 3如图3-34(b )所示,其参考方向与树支电压方向相同。
(3) 写基本割集的KCL 方程。
图3-34 例3-16图
5s (a )
(b )
C 12
C 3
为写方程方便起见,将基本割集C 1、C 2、C 3画在原电路上,如图3-34(c )所示。
每一条支路的电流都可以用树支电压以及激励源表示。
对应基本割集的KCL 方程分别为
03
2
1511123=++-+---R u u R u u R u u u s (1)
011
233
2142=---+++-R u u u R u u R u i s (2)
02
3
1123=++--s i R u R u u u (3)
(4) 联立求解,得树支电压u 1、u 2、u 3。
(5) 利用树支电压求得电路的其它物理量。
(c )
s C 3
C
C C 2
C 3
(d )
图3-34 例3-16图
如所选树如图3-34(d )所示,则所得基本割集方程正好是结点电压方程,所以结点电压法是割集分析法的特例。
例3-17 重做例3-7所示电路。
求结点①与结点②之间的
电压12u 。
解:选树支电压如图,分别为u 1、u 2和u 3 。
u 3等于22V ,可以不建立关于u 3的基本割集方程。
另外两个基本割集的KCL 方程分别为
C 1 08)1(3)22(411=+++-u u C 2 025)22(51822=-++⨯+u u 两式联立求解得
V u 111=,V u 5.152-= 所以 V u u 11
112==
4S
2
图3-35 例3-17图
例3-18 电路如图3-36(a )所示。
已知:
S G 11=,S G 2 2=,S G 3 3=,S G 5 5=,V u s 1 1=, V u s 3 3=,
A i s 3 3=, 4 4V u s =,V u s 6 6=。
试用割集分析法求电流i 1以
及电压源u s1发出的功率p 。
解:选树如图粗线所示,树支电压如图3-36(b )所示,为u 1、u 4和u 6。
因为V u u s 4 44==,V u u s 6 66== ,所以可以不建立关于u 4和u 6的基本割集方程,故只需要列关于u 1的基本割集方程。
基本割集C 1如图3-36(a )所画,其方程为
0)()()(36145612111=+++-+++-s s s s s i u u u G u u G u u G
图3-36 例3-18图
u s4(a )
(b )
即 024 81=+u 得 V u 3 1-=
所以 A u u G i s 4)13()(1111-=--=-= W i u p s 411=-=。