电路分析中回路分析法和割集分析法共27页

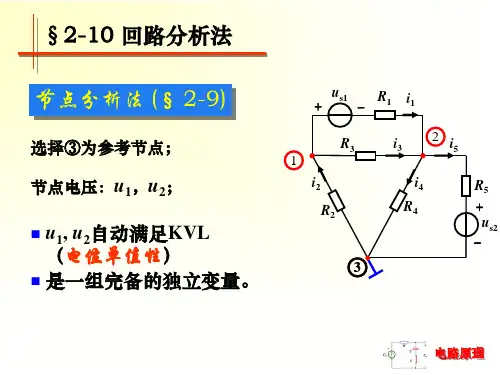
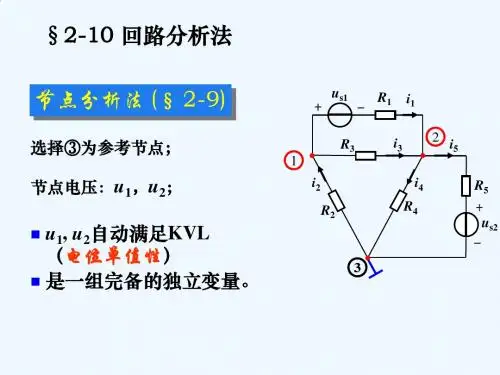
§2-6 回路分析法及网孔分析法1、物理描述回路分析法（loop-analysis method）的基本指导思想是用未知的回路电流代替未知的支路电流来建立电路方程，以减少联立方程的元数。

对于只隶属于一个回路的支路，其电流即等于该支路所属回路的回路电流；对于两个（或两个以上）回路的公共支路，其电流可按基尔霍夫电流定律求解。

对于平面电路，可以按网孔取独立回路，以网孔电流(mesh current)为变量，按照基尔霍夫电压定律和元件方程列出网孔电压方程（简称网孔方程）。

这种方法称为网孔分析法（mesh-analysis method）。

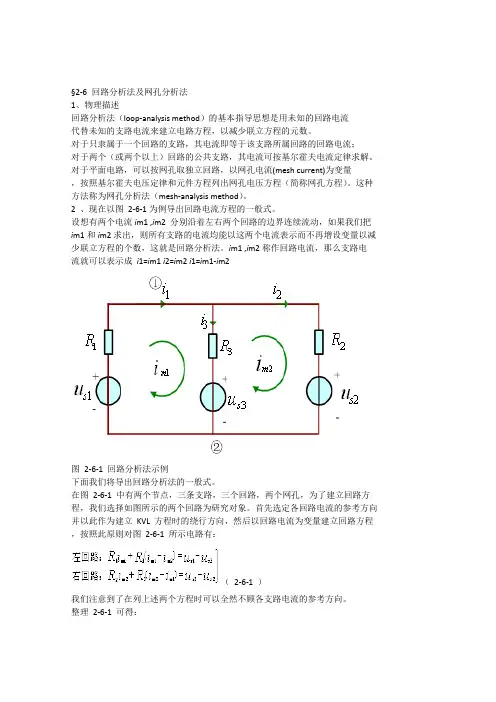
2 、现在以图2-6-1为例导出回路电流方程的一般式。

设想有两个电流i m1 ,i m2 分别沿着左右两个回路的边界连续流动，如果我们把i m1和i m2求出，则所有支路的电流均能以这两个电流表示而不再增设变量以减少联立方程的个数，这就是回路分析法。

i m1 ,i m2称作回路电流，那么支路电流就可以表示成i1=i m1 i2=i m2 i1=i m1-i m2图2-6-1 回路分析法示例下面我们将导出回路分析法的一般式。

在图2-6-1 中有两个节点，三条支路，三个回路，两个网孔，为了建立回路方程，我们选择如图所示的两个回路为研究对象。

首先选定各回路电流的参考方向并以此作为建立KVL 方程时的绕行方向，然后以回路电流为变量建立回路方程，按照此原则对图2-6-1 所示电路有：（2-6-1 ）我们注意到了在列上述两个方程时可以全然不顾各支路电流的参考方向。

整理2-6-1 可得：（2-6-2 ）式（2-6-2 ）是以回路电流为求解对象的回路电流方程。

解式（2-6-2 ）可得回路电流i m1 ,i m2 ，进而可得各支路电流i1 ,i2 ,i3。

我们只需解两个联立方程便可算出3 个未知的支路电流。

可见在以回路电流为变量时可以减少联立方程的个数。

方程的数目应该等于独立回路数。

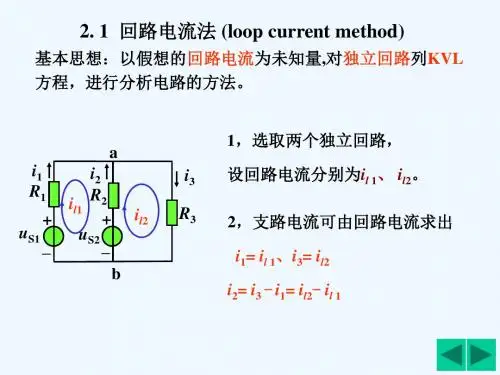
§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②③①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。