控制系统的微分方程描述
- 格式:docx
- 大小:129.08 KB
- 文档页数:2








控制系统的微分方程数学模型:描述系统输入、输出变量以及内部各变量之间关系的数学表达式。
描述各变量动态关系的表达式称为动态数学模型,常用的动态模型为微分方程。
建立数学模型的方法分为解析法和实验法。
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(阶跃信号、单位脉冲信号、正弦信号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
建立微分方程的步骤:1、分析各元件的工作原理,明确输入、输出量;2、按照信号的传递顺序,列写各变量的动态关系式;3、化简(线性化、消去中间变量),写出输入、输出变量间的数学表达式。
例:RLC 无源网络如图所示,图中R 、L 、C 分别为电阻(Ω)、电感(H)、电容(F);建立输入电压u r (V)和输出电压u c (V)之间的动态方程。
解由基尔霍夫定律得:()1()()()r di t u t Ri t L i t dt dt C=++⎰1()()c C u t i t dt=⎰消去中间变量i (t ),可得:222()d ()2()()c c c rd u t u t T T u t u t dt dt ζ++=22()()()()c c c rd u t du t LC RC u t u t dt dt ++=令,则微分方程为:2,2LC T RC T ζ==式中:T 称为时间常数,单位为s,称为阻尼比,无量纲。
ζ例设有一弹簧、质量块、阻尼器组成的系统如图所示,当外力F 作用于系统时,系统将产生运动。
建立外力F 与质量块位移y (t )之间的动态方程。
其中弹簧的弹性系数为k ,阻尼器的阻尼系数为f ,质量块的质量为m 。
解对质量块进行受力分析,作用在质量块上的力有:外力: F 弹簧恢复力:Ky(t)阻尼力:()dy t f dt由牛顿第二定律得:22()()()d y t dy t m F f Ky t dt dt =−−22()()()d y t dy t m f Ky t Fdt dt ++=222()()2()d y t dy t T T y t kFdt dt ζ++=令,,/T m K =2/T f K ζ=1/k K =/2f mKζ=则微分方程可以写为该方程描述了由质量块、弹簧和阻尼器组成系统的动态关系,它是一个二阶线性定常微分方程。
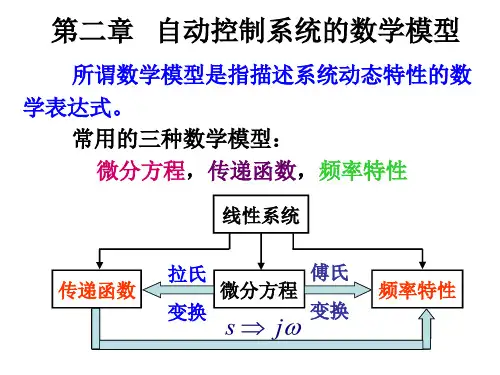

第四节 控制系统的微分方程及线性化方程一、基本概念1、系统的微分方程——在时域内用来描述系统及其输入、输出三者之间的动态关系的数学模型。
(包括系统动态方程、运动方程或动力学模型)2、建立微分方程——根据支配系统动态特性的各种物理规律(力学、电学、液压等各种原理和规律),明确输入(一般为已知函数)和输出(一般作待求的未知函数),列出微分方程,并整理为标准形式(含输出项在等式左边,含输入项在等式右边,并按微分降幂排列)。
二、系统分类1、线性系统可用线性微分方程描述的系统。
(1)线性定常系统—线性微分方程中的系数与时间无关的系统。
(2)线性时变系统—线性微分方程中的系数与时间相关的系统。
特点:可应用线性加原理,分别处理各项输入引起的输出,最后将结果叠加。
2、非线性系统必须用非线性微分方程描述的系统,不能使用叠加原理。
本课程属经典控制论范畴,主要研究线性定常系统!三、微分方程的建立1、位移系统中元件的复阻抗(1)弹簧)的正方向相同,无论时受压还是受拉,都有:()()=f t Kx t即: ()()=F s Kx s(K为弹簧刚度系数)(为速度阻尼系数) B(M为质量)输入:()f t作用力 输出:()x t线位移根据牛顿第二定律F ma =设质量块正方向移动()x t ,()f t 作用力要克服弹簧和阻尼器的阻力K f 和B f 。
即:()()()()()K B f t f f maf t Kx t Bx t Mx t −−=⇒−−=移项标准化:()()()()Mxt Bx t Kx t f t ++=J K ——扭转弹簧刚度系数(N m ⋅/)rad τ——外加力矩(N m ⋅)J B ——转动粘性阻尼(/) N m s ⋅⋅rad 解:输入为力矩τ,输出为转角()t θ 根据转矩公式:M J ε=⋅力矩τ要使系统进行转动的话,必须克服弹簧和阻尼器的阻力矩。
()()()()J J J J K t B w J K t B t J t τθετθθ−⋅−⋅=⋅⇒−⋅−⋅= θ整理得:()()()J JJ t B t K t θθθτ+⋅+⋅= 例3:已知电机转矩为,负载转矩为m T L T ,为齿轮齿数,为各轴系粘性转动动阻尼系数,为各轴系转动惯量,i Z i B i J i θ为各轴系的角位移。
1-3自动控制系统的分类之吉白夕凡创作本课程的主要内容是研究按偏差控制的系统。
为了更好的了解自动控制系统的特点,介绍一下自动控制系统的分类。
分类方法很多,这里主要介绍其中比较重要的几种:一、按描述系统的微分方程分类在数学上通常可以用微分方程来描述控制系统的动态特性。
按描述系统运动的微分方程可将系统分成两类:1.线性自动控制系统描述系统运动的微分方程是线性微分方程。
如方程的系数为常数,则称为定常线性自动控制系统;相反,如系数不是常数而是时间t的函数,则称为变系数线性自动控制系统。
线性系统的特点是可以应用叠加原理,因此数学上较容易处理。
2.非线性自动控制系统描述系统的微分方程是非线性微分方程。
非线性系统一般不克不及应用叠加原理,因此数学上处理比较困难,至今尚没有通用的处理方法。
严格地说,在实践中,理想的线性系统是不存在的,但是如果对于所研究的问题,非线性的影响不很严重时,则可近似地看成线性系统。
同样,实际上理想的定常系统也是不存在的,但如果系数变更比较缓慢,也可以近似地看成线性定常系统。
二、按系统中传递信号的性质分类1.连续系统系统中传递的信号都是时间的连续函数,则称为连续系统。
2.采样系统系统中至少有一处,传递的信号是时间的离散信号,则称为采样系统,或离散系统。
三、按控制信号r(t)的变更规律分类1.镇定系统()r t为恒值的系统称为镇定系统(图1-2所示系统就是一例)。
2.程序控制系统()r t为事先给定的时间函数的系统称为程序控制系统(图1-11所示系统就是一例)。
3.随动系统()r t为事先未知的时间函数的系统称为随动系统,或跟踪系统,如图1-7所示的位置随动系统及函数记录仪系统。
第三节自动控制系统的分类控制系统的分类方法:按控制方式分:开环控制,闭环控制,复合控制等;按系统性能分:线性系统和非线性系统、连续系统和离散系统、定常系统和时变系统。
线性连续控制系统计算机控制系统的分类作者: cips发表日期: 2006-02-08 15:43 复制链接计算机控制系统的分类有三种方法:以自动控制行式分类,以参于控制方式分类或以调节规律分类。
控制系统的微分方程描述 1. 确定每个环节或者整个系统的输入量和输出量 2. 列出各环节的微分方程 3. 消去中间变量
4. 化为标准型Xi=f (Xo (t ))
R-C 电源网络,机械元件之间合力位移加速度关系
u i (t )u o (t )R 1R 2
C L
根据电路的定理,
11()()()i C u t i t R i t dt C =+⎰
2()1()()L C L di t i t dt L i t R C dt =+⎰
2()()o L u t i t R = ()()()C L i t i t i t +=
所以消去变量最后就可以得到微分关系式
对于弹簧类的题目,
M
D K f (t )
x o (t )
x i (t )f(t)外力,求输入输出位移之间的动态关系式?
根据弹簧弹力有,()1()()-()i o f t K x t x t =。
阻尼器阻尼力有,2()
()o dx t f t D dt =
根据牛二定律有,2122()()()o d x t f t f t M dt -=,F=ma ,a 为x 的二次导数
所以消去中间变量,)()()()(22t Kx t Kx dt t dx D dt t x d M i o o o =++
1. 阻尼器的力的方向?
2. 受力分析写出,所以要how 分析?-这不物理吗
继续,
根据牛二定律,受力分析,2122()()()()d x t f t f t f t m dt --= D m K f (t ) x(t)
)()(1t Kx t f = dt t dx D t f )()(2=,所以可以看出阻尼器的力应该是向上 整理得,)()()()(22t f t Kx dt t dx D dt t x d m =++
所以关键是受力分析,大小表达式,方向。