沪科版9上数学练习题 相似三角形及利用平行线判定相似三角形

24.2相似三角形的判定第1题. 如图，AC BD ⊥，垂足为C ，过D 点作DF AB ⊥，垂足为F ，交AC 于E 点．请找出图中所有的相似三角形，并说明理由．答案：解：（1）因为90A A AFE ACB ∠=∠∠=∠=， 所以AFE ACB △∽△．（2）因为90AEF DEC AFE DCE ∠=∠∠=∠=，， 所以AFE DCE △∽△． 所以A D ∠=∠．（3）因为A D ∠=∠，90AFE DFB ∠=∠=， 所以AFE DFB △∽△．（4）因为D A ∠=∠，90DCE ACB ∠=∠=， 所以DCE ACB △∽△．（5）因为D A ∠=∠，90DFB ACB ∠=∠=， 所以DFB ACB △∽△．（6）因为D A ∠=∠，90DCE DFB ∠=∠=， 所以DCE DFB △∽△．知识点：三角形相似的条件 试题类型：运算题 试题难度：容易 考查目标：基本技能 第2题.如图，一艘军舰从点A 向位于正东方向的C 岛航行，在点A 处测得B 岛在其北偏东75，航行75nmile 到达点D 处，测得B 岛在其北偏东15，继续航行5n mile 到达C 岛，此时接到通知，要求这艘军舰在半小时内赶到正北方向的B 岛执行任务，则这艘军舰航行速度至少为多少时才能按时赶到B 岛？答案：解：根据题意，可得1590A CBD BCD ACB ∠=∠=∠=∠=，．所以.BCD ACB △∽△ 由相似三角形对应边成比例，得BC AC DC BC =，即805BC BC=． ＡＦＢＣＤＥＡＤ所以240020BC BC ==，．要求军舰在半小时内赶到正北方向的B 岛执行任务，因此航行速度至少是200.540=÷(n mile/h)知识点：三角形相似的条件 试题类型：应用题 试题难度：中等 考查目标：双基简单应用 第3题. 如图，点E C 、分别在AB AD 、上，BC 与DE 相交于一点O ，若B D ∠=∠， 则图中相似三角形有几对？分别写出来说明理由． 答案：2对BAC DAE BOE DOC △∽△，△∽△．理由略知识点：三角形相似的条件 试题类型：运算题 试题难度：容易考查目标：基本技能 第4题. 如图，已知:3:4DE BC AD DB =∥，，若5DE =cm ，求BC 的长． 答案：353cm 知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：基本技能 第5题. 如图，已知ABC ACB ∠=∠，若3AD =cm ，7AB =cm ，试求AC 的长．21cm知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：基本技能第6题. 如图，4cm 9cm 5cm 12cm AO DO AB BC O ====，，，，为BC 的中点，求CDO △的周长．答案：解：由12cm BC =，O 为BC 的中点，得6BO CO ==cm ．由4cm 9cm AO DO ==，，得23AO BO CO DO ==． 因为两边对应成比例且夹角相等的两个三角形相似， 所以AOB COD △∽△． 由相似三角形对应边成比例，得AB AO CD CO =，即523CD =． ＡＣＯ Ｄ ＢＥ ＡＤＥＣ Ｂ Ａ ＤＣＡＢＯＣ所以537.52CD ==×(cm)． 因此，CDO △的周长是67.5922.5++=(cm)．知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：基本技能 第7题. 已知ABC △的三条边长之比为3:7:9，与其相似的另一个A B C '''△最大的边长为18cm ，则A B C '''△最小的边长为cm ，周长为cm ． 答案：6 38知识点：三角形相似的条件 试题类型：填空题 试题难度：容易 考查目标：基本技能 第8题. 如图，在ABC △中，点D E 、分别在边AC AB 、上，且23AE AD AC AB ==，若4DE =cm ，则BC =cm ．答案：6知识点：三角形相似的条件 试题类型：填空题 试题难度：中等 考查目标：基本技能第9题.如图，点D E 、分别为边AB AC 、的三等分点（即：1133AD AB AE AC ==，），若22.5cm ADE S =△，求ABC S △的大小．答案：222.5cm知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：双基简单应用 第10题. 如图，在ABC △中，345AB AC BC D ===，，，是AB 上的一点，2AD =，在AC 上是否存在一点E ，使A D E 、、三点组成的三角形与ABC △相似？如果存在，请求出AE 的长；如果不存在，请说明理由．答案：解：存在．因为22225AB AC BC +==，所以ABC △是直角三角形，90A ∠=． 设所求AE 的长为x ，在ADE △与ABC △中，90A A ∠=∠=， （1）若AD AEAB AC=，则ADE △∽ABC △． ＡＥ ＢＤ ＡＤ Ｅ Ｃ Ｂ ＡＤ ＢＣ此时234x =． 解得83x =．（2）若AD AEAC AB =，则ADE ACB △∽△． 此时243x =．解得32x =．所以，当AE 取83或32时，A D E 、、三点组成的三角形与ABC △相似．知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：双基简单应用 第11题. 如图，下列条件中不能判定ACD ABC △∽△的是（ ） (A)AB ADBC CD=(B)ADC ACB ∠=∠ (C)ACD B ∠=∠(D)2AC AD AB =答案：(A)知识点：三角形相似的条件 试题类型：选择题 试题难度：中等 考查目标：基本技能 第12题. 已知：如图，点C D ，在线段AB 上，PCD △是等边三角形．（1）当AC CD DB ，，满足怎样的关系式时ACP PDB △∽△；（2）当ACP PDB △∽△时，求APB ∠的度数．答案：解：（1）当2CD AC DB =时，ACP PDB △∽△； （2）当ACP PDB △∽△时，120APB ∠=．知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：数学思考第13题. 在ABC △和A B C '''△中，326cm 10cm 32A AB A B A '''∠===∠=，，，， 3cm AC =，5cm A C ''=，则ABC △与A B C '''△是否相似？（填“是”或“不是”）． 答案：是知识点：三角形相似的条件 试题类型：填空题 试题难度：容易 考查目标：基本技能 第14题. 下列四组图形中不一定相似的是． Ａ．有一个角等于40的两个等腰三角形ＡＣ Ｄ Ｂ ＰＡ Ｃ Ｄ ＢＢ．有一个角为50的两个直角三角形Ｃ．直角三角形被斜边上的高分成的两个直角三角形 Ｄ．有一个角是60的两个等腰三角形 答案：Ａ知识点：三角形相似的条件 试题类型：选择题 试题难度：容易 考查目标：基本技能 第15题. 能判定ABC △与A B C '''△相似的条件是．Ａ．ABAC A B A C =''''Ｂ．AB A B AC A C ''=''，且A C '∠=∠ Ｃ．AB BC A B A C =''''且B A '∠=∠Ｄ．AB ACA B A C =''''，且B B '∠=∠ 答案：Ｃ知识点：三角形相似的条件 试题类型：选择题 试题难度：容易 考查目标：基本技能 第16题.已知：如图，9086ABD BCD AB BD ∠=∠===，，，当BC 为多少时，图中的两个三角形相似． 答案：BC 为3.6或4.8知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：双基简单应用第17题. 如图，线段AC BD ，相交于点O ，要使AOB DOC △∽△，已具备条件，还需要补充的条件是，或或．答案：BO OAAOB DOC B C A D OC OD ∠=∠∠=∠∠=∠=，，，知识点：三角形相似的条件 试题类型：填空题 试题难度：容易 考查目标：基本技能 第18题.如图，D 为ABC △的边BC 上的一点，连接AD ，要使ABD CBA △∽△，应具备下列条件中的（ ）Ａ．AC AB CD BD =Ｂ．2AB BD BC = Ｃ．AB BC CD AD=Ｄ．2AC CD CB = 答案：Ｂ知识点：三角形相似的条件 试题类型：选择题 试题难度：容易 考查目标：基本技能 第19题. 如图，已知1234∠=∠∠=∠，． （1）图中有哪几对相似三角形？把它们写出来；ＡＢＣＡ ＤＯＢ ＡＢＤ（2）证明你所写出的结论．答案：（1）解：图中的相似三角形有三对，它们分别是AOD BOC AOBDOC △∽△，△∽△， ABD EBC △∽△ （2）证明：12AOD BOC ∠=∠∠=∠，，AOD BOC ∴△∽△，AO OD OB OC =，即AO OBOD OC=， 又DOC AOB ∠=∠，AOB DOC ∴△∽△又34∠=∠，43EBD EBO ∴∠+∠=∠+∠即ABD EBC ∠=∠ABD EBC ∴△∽△．知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：双基简单应用 第20题. 如图12，P 是y 轴上一动点，是否存在平行于y 轴的直线x t =，使它与直线y x =和直线122y x =-+分别交于点D E 、（E 在D 的上方），且PDE △为等腰直角三角 形．若存在，求t 的值及点P 的坐标；若不存在，请说明原因．答案：解：存在．方法一：当x t =时，y x t ==；当t =时，112222y x t =-+=-+． E ∴点坐标为1(2)2t t -+，，D 点坐标为(t t ，． E 在D 的上方，132222DE t t t ∴=-+-=-+，且43t <．3分PDE △为等腰直角三角形，PE DE PD DE PE PD ∴===或或． 若022t PE DE t t >=-+=3，时，， 4182.525t t ∴=-+=，P ∴点坐标为805⎛⎫ ⎪⎝⎭，．若3022t PD DE t t >=-+=，时，， ＤＡＣ ＢＯ Ｅ1 234图12O122y x =-+y x = y x4.5t P ∴=∴点坐标为405⎛⎫ ⎪⎝⎭，．若0t PE PD >=，时，即DE 为斜边，322.2t t ∴-+= 47t DE ∴=，的中点坐标为114t t P ⎛⎫+∴ ⎪⎝⎭，，点坐标为807⎛⎫⎪⎝⎭，． 若0t PE DE PD DE <==，和时，由已知得32402DE t t t t =--+=-=>，， （不符合题意，舍去）， 此时直线x t =不存在．若0t <，PE PD =时，即DE 为斜边，由已知得32222DE t t t =--+=-，， 14104t t P ∴=-+=∴，，点坐标为(00)，． 综上所述：当45t =时，PDE △为等腰直角三角形，此时Ｐ点坐标为805⎛⎫ ⎪⎝⎭，或 405⎛⎫ ⎪⎝⎭，；当47t =时，PDE △为等腰直角三角形，此时Ｐ点坐标为807⎛⎫⎪⎝⎭，；当4t =-时，PDE △为等腰直角三角形，此时Ｐ点坐标为(00)，． 方法二：设直线122y x =-+交y 轴于点A ，交直线y x =于点B ，过B 点作BM 垂直于y 轴，垂足为M ，交DE 于点N ．x t =平行于y 轴，MN t ∴=．43142..23y x x y x y ⎧==⎧⎪⎪⎪⎨⎨=-+⎪⎪=⎩⎪⎩，，解得B ∴点坐标为444.333BM ⎛⎫∴= ⎪⎝⎭，， 2分当0x =时，1222y x A =-+=∴，点坐标为(02) 2.OA ∴=，，3分PDE △为等腰直角三角形，.PE DE PD DE PE PD ∴===或或如图４，若0t PE DE >=，和PD DE =时，PE t PD t DE OA ∴==，，∥，BDE BOA ∴△∽△，DE BNOA BM∴=．443.4253t t t -∴=∴=，当45t =时，1842.255y x y x =-+===，P ∴点坐标为805⎛⎫ ⎪⎝⎭，或405⎛⎫ ⎪⎝⎭，．若0t PD PE >=，时，即DE 为斜边，22DE MN t ∴==．.DE BNDE OA BDE BOA OA BM∴∴∴=∥，△∽△， 42434273MNMN MN t DE -∴=∴==，，中点的纵坐标为181.47t P +=∴点坐标为807⎛⎫⎪⎝⎭， 如图5，若0t PE DE PD DE <==，或时，DE OA ∥，.DE BNBDE BOA OA BM∴∴=△∽△， 4DE =-（不符合题意，舍去），此时直线x t =存在． 10分若0t PE PD <=，时，即DE 为斜边，22DE MN t ∴==-..DE BNDE OA BDE BOA OA BM∴∴=∥，△∽△4213 4.4104243MNMN MN t t +∴=∴=∴=-+=，，P ∴点坐标为（０，０）． 综上述所述：当45t =时，PDE △为等腰直角三角形，此时P 点坐标为805⎛⎫ ⎪⎝⎭，或 405⎛⎫ ⎪⎝⎭，；当47t =时，PDE △为等腰直角三角形，此时P 点坐标为807⎛⎫⎪⎝⎭，；当 4t =-时，PDE △为等腰直角三角形，此时P 点坐标为（０，０）． 知识点：6 探索三角形相似的条件 综合知识点 试题类型：合情推理题 试题难度：较难 考查目标：数学思考图5OyxDNMEABx 图4OyD N MEAB………………………………………………最新资料推荐……………………………………… 第21题.如图，P 是Rt ABC △的斜边BC 上异于B 、C P 点作直线截ABC △，使截得的三角形与ABC △相似，满足这样条件 的直线共有（ ）条Ａ．1 Ｂ．2 Ｃ．3 Ｄ．4 答案：C知识点：三角形相似的条件 试题类型：选择题 试题难度：中等 考查目标：数学思考第22题. ．如图５，ABCD 是平行四边形，则图中与DEF △相似的三角形 共有（ ） (A)１个 (B)２分(C)３个(D)4个答案：B知识点：三角形相似的条件 试题类型：选择题 试题难度：容易 考查目标：基础知识 第23题. 如图，梯形ABCD 中，AD //BC ，BD 为对角线，中位线EF 交BD 于O 点，若FO －EO =3，则BC －AD 等于A ．4B ．6C ．8D ．10答案：B试题号：13094 知识点：三角形相似的条件 试题类型：选择题 试题难度：中等 考查目标：双基简单应用 录入时间：2005-9-15(13134)第24题. 如图，AF CE ⊥，垂足为点21O AO CO EO FO ====，，． （1）求证：点F BC 为的中点； （2）求四边形BEOF 的面积． 答案：解：（1）连结EF AC ， ∵21AO CO EO FO ====，， 12EO FO OCOA==∴． EF AC ∴∥．BＡＢCDE F图５第12题 OCFEBAOFEB………………………………………………最新资料推荐………………………………………12BF EF EO BC AC OC ===∴． F BC ∴为的中点．（2）由（1）知，F BC 为的中点．113(21)1222BEF CEFSSCE OF ===⨯+⨯=∴． 又11111222OEF S OE OF ==⨯⨯=，∴31222BEF OEF BEOF S S S =+=+=四边形知识点：三角形相似的条件 试题类型：运算题 试题难度：中等 考查目标：双基简单应用 第25题. 小胖和小瘦去公园玩标准的．．．跷跷板游戏，两同学越玩越开心，小胖对小瘦说：“真可惜！我只能将你最高翘到1米高，如果我俩各边的跷跷板都再伸长相同的一段长度，那么我 就能翘到1米25，甚至更高！”（1）你认为小胖的话对吗？请你作图分析说明； （2）你能否找出将小瘦翘到1米25高的方法？试说明． 解：答案：解：（1）小胖的话不对．小胖说“真可惜！我现在只能将你最高翘到1 米高”，情形如图（1）所示，OP 是标准跷跷板支架的高度，AC 是跷跷板一端能翘到的最 高高度1米，BC 是地面．.OP BC AC BC OBP ABC OBP ABC ∠=∠∴⊥，⊥，，△∽△.BO OPBA AC∴= 又此跷跷板是标准跷跷板，BO OA =，12BO BA ∴=，而1AC =米，得0.5OP =米． 若将两端同时都再伸长相同的长度，假设为a 米(0)a >． 如图（2）所示，BD a =米，AE a =米BO OA BO a OA a =∴+=+，，即DO OE =．地面Ｐ第23题图ＯＡＢＥ………………………………………………最新资料推荐………………………………………11 / 1112DO DE ∴=，同理可得DOP DEF △∽△． DO OPDE EF ∴=，由0.5OP =米，得1EF =米．综上所述，跷跷板两边同时都再伸长相同的一段长度， 跷跷板能翘到的最高高度始终为支架OP 高度的两倍， 所以不可能翘得更高．（2）方案一：如图（3）所示，保持BO 长度不变．将 OA 延长一半至E ，即只将小瘦一边伸长一半． 使12AE OA =，则25BO BE =． 由BOP BEF △∽△，得.BO OPBE EF= 1.25EF ∴=米．方案二：如图（4）所示，只将支架升高0.125米．12B O B O P B AC B A ''''''''=''，△∽△，又0.50.1250.625O P ''=+=米．B O O P B A A C''''∴=''''． 1.25A C ''∴=米． （注：其它方案正确，可参照上述方案评分！）知识点：6 探索三角形相似的条件 综合知识点 试题类型：运算题 试题难度：中等 考查目标：双基简单应用第26题. 在△ABC 中，DE BC ∥，2AD =，3AE =，4BD =，则AC =． 答案：9知识点：6 探索三角形相似的条件 综合知识点 试题类型：填空题 试题难度：容易 考查目标：基础知识ＯＣ Ａ（3）FＥA '（4）CP 'B 'O '。

沪科版九上数学相似三角形练习题一、选择题1、下列各组图形中不是位似图形的是（）A．B．C．D．2、若2：3=7：x，则x=（）A．2B．3C．3.5D．10.53、两个相似三角形的一组对应边分别为5cm和3cm，如果它们的面积之和为136cm2，则较大三角形的面积是（）A．36cm2B．85cm2C．96cm2D．100cm24、如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD，若B（1，0），则点C的坐标为（）A．（1，-2）B．（-2，1）C．（）D．（1，-1）5、如图，已知点A在反比例函数y=(x < 0)上，作Rt△ABC，点D是斜边AC的中点，连DB并延长交y轴于点E，若△BCE的面积为8，则k的值为( )A .8B .12C .16D .206、如图，平面直角坐标系中，直线y=-x+a与x、y轴的正半轴分别交于点B和点A，与反比例函数y=-的图象交于点C，若BA：AC=2：1，则a的值为（）A．2B．-2C．3D．-37、如图，△ABC与△DEF是位似图形，位似比为2：3，已知AB=4，则DE的长等于( )A .6B .5C .9D .8、如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于( )A .5∶8B .3∶8C .3∶5D .2∶59、如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③=；④=AD•AB．其中单独能够判定△ABC∽△ACD的个数为( )A .1B .2C .3D .410、如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，动点P从点B出发，沿着B-A-D在菱形ABCD的边上运动，运动到点D停止，点P′是点P关于BD的对称点，PP′交BD于点M，若BM=x，△OPP′的面积为y，则y与x之间的函数图象大致为（）A ．B ．C ．D ．11、在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为（4，3）．平行于对角线AC 的直线m 从原点O 出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边分别交于点M ，N ，直线m 运动的时间为t （秒）．设△OMN 的面积为S ，则能反映S 与t 之间函数关系的大致图象是（ ）A ．B ．C ．D ．12、如图，已知在梯形ABCD 中，AD∥BC，BC=2AD ，如果对角线AC 与BD 相交于点O ，△AOB、△BOC、△COD、△DOA 的面积分别记作S 1、S 2、S 3、S 4，那么下列结论中，不正确的是（）A．S1=S3B．S2=2S4C．S2=2S1D．S1•S3=S2•S4二、填空题13、如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是 __________ cm．14、如图，在△PMN中，点A、B分别在MP和NP的延长线上，==，则= __________ ．三、解答题15、已知=,求下列算式的值．（1）;（2）16、如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．（1）求证：△AEH∽△ABC；（2）求这个正方形的边长与面积。

沪科版九年级上册相似三角形的性质习题1.若ΔABC∽ΔA'B'C'.相似比为1:2,则ΔABC 与ΔA'B'C'的面积的比为A.1:2B.2:1C.1:4D.4:12.如图，AB//CD,32 OD AO ,则ΔAOB 的周长与ΔDOC 周长的比值是( ) A.52 B.23 C.84 D.32 3.如图，在梯形ABCD 中，AD//BC,/B=ZACD=90°,AB=2,DC=3,则ΔABC 与ΔDCA 的面积比为（ )A.2:3B.2:5C.4:9D.3:24.如图，DE 是ΔABC 的中位线，则ΔADE 与ΔABC 的面积比为_______.5. 在ΔABC 中，D 、E 分别是边AB 、AC 的中点，BC=4,下列四个结论：①DE=2;②ΔADE∽ΔABC;③AA DE 的面积与ΔABC 的面积之比为1:4;④ΔADE 的周长与ΔABC 的周长之比为1:4.其中正确的有________（填序号）。

6. 在ΔABC 中，ED 交AB 于点E,交AC 于点D,53==AC AE AB AD ,且ΔABC 与ΔADE 的周长之差是16cm,求ΔABC 和ΔADE 的周长。

7. 如图，在平行四边形ABCD 中，E 是AD 边上的中点，连接BE,并延长BE 交CD 的延长线于点F,则ΔEDF 与ΔBCF 的周长之比是( )A.1:2B.1:3D.1:5C.1:48.如图，在ΔABC 中．∠C=90°,将ΔABC 沿直线M.N 翻折后，顶点C 恰好落在AB 边上的点D 处，已知MN//AB.MC=6.NC=32,则四边形MABN 的面积是（ ） A.36 B.312 C.318D. 3249.如图，在ΔABC 中，D 、E 分别是AB 、BC 上的点，且DE//AC,若S ΔBDE :S ΔCDE =1:4,则S ΔBDE :S ΔADC 为（ )A.1:16B.1:18C.1:20D.1:2410. 兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为( )A.11.5米B.11.75米C.11.8米D.12.25米11.已知ΔABC∽ΔA'B'C',相似比为3:4,ΔABC 的周长为6,则ΔA'B'C'的周长为_____.12.如图，在平行四边形ABCD 中，CD=10,F 是AB 边上一点，DF 交AC 于点E,且52 EC AE ,则CDE AEF S S =______,BF=_______.13.一天晚上，李明和张龙利用灯光下的影长来测量一路灯D 的高度．如图，当李明走到点A 处时，张龙测得李明直立时的身高AM 与其影长AE 正好相等，接着李明沿AC 方向继续向前走，走到点B 处时，测得李明直立时的身高BN 与其影长线段AB,并测得AB=1.25m.已知李明直立时的身高为1.75m,求路灯CD 的高度（结果精确到0.1m).14.如图，有一边长为5cm 的正方形ABCD 和等腰三角形PQR,PQ=PR=5cm,QR=8cm,点B 、C 、Q 、R 在同一条直线l 上，当C 、Q 两点重合时，等腰三角形PQR 以1cm/s 的速度沿直线l 按箭头所示方向开始匀速运动，ts 后正方形ABCD 与等腰三角形PQR 重合部分的面积为S(c ㎡),解答下面的问题：（1)当t=3时，求S 的值；（2)当t=5时，求S 的值．1、最困难的事就是认识自己。

上海,数学,学科,九年级,相似,三角形,测试题,相似三角形测试题及答案图形的放缩与比例线段（1）一、填空题（每小题4分，共40分）1、如果，那么＝________。

2、已知：，则＝________。

3、与的比例中项是________。

4、对一段长为20cm的线段进行黄金分割，那么分得的较长线段长为________cm。

（不取近似值）5、如图，DE∥BC，AD＝1，DB＝2，则的值为________。

6、如图，DE∥BC，AB＝12，AC＝16，AE＝10，则AD＝________。

7、如图，线段AB＝10cm，，，则CD＝________cm。

8、已知：线段AB＝10cm，点C是AB的黄金分割点，且AC＞CB，则BC＝________cm。

（不取近似值）9、如图，AD∥EF∥BC，，DF＝4cm，则DC＝________cm。

10、如图，AB∥EF∥DC，AB＝，DC＝，，则EF＝________。

（用式子表示）二、选择题（每小题4分，共16分）1、若，则下列等式中不正确的是（）。

（A）；（B）；（C）；（D）。

2、如图，△ABC中，DE∥BC，则下列等式中不成立的是（）。

（A）；（B）；（C）；（D）。

3、如图，△ABC中，DE∥BC，AD＝1，EC＝3，则下列等式中成立的是（）。

（A）；（B）；（C）；（D）。

4、如图，△ABC中，DE∥BC，AD＝1，DB＝DE＝2，则BC长是（）。

（A）3；（B）4；（C）5；（D）6。

三、（本题8分）如图，△ABC中，DE∥BC，EF∥AB，，FC＝2，AC＝6，求DE和CE长四、（本题8分）如图，△ABC中，AD＝2DC，G是BD中点，AC延长线交BC于E，求的值。

五、（本题8分）如图，△ABC中，DE∥BC，AH⊥BC于F，AH交DE于G，DE＝10，BC＝15，AG＝12，求线段AH 长。

六、（本题10分）如图，平行四边形ABCD中，E是AB的中点，G是AC上一点，，连EC延长交AD于F，求的值。

相似三角形的判定一、选择题1．如图，在平行四边形ABCD中，AB＝10，AD＝6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则BF的长是( )A．5 B．8.2C．6.4 D．1.82．如图所示，小正方形的边长均为1，则下列选项中阴影部分的三角形与△ABC相似的是( )3.如图，在平行四边形ABCD中，过点B的直线与对角线AC、边AD分别交于点E和点F，过点E作EG∥BC，交AB于G，则图中相似的三角形有( )A.4对B.5对C.6对D.7对4.有下列判断：①顶角相等的两个等腰三角形相似；②有一个角相等的两个等腰三角形相似；③直角三角形都相似；④若一个三角形的两边长分别为2、6，夹角为32°，另一个三角形的两边长分别为3、9，夹角为32°，则这两个三角形相似.其中判断正确的有( )A.1个B.2个C.3个D.4个5.有下列说法：①有一个角为50°的两个等腰三角形相似；②有一个角为100°的两个等腰三角形相似；③有一个锐角相等的两个直角三角形相似；④两个等边三角形相似。

其中正确的有( )A.1个B.2个C.3个D.4个二、填空题6.如图，有下列条件：①∠B=∠C;②∠ADB=∠AEC；③AD AEAC AB=；④AD AEAB AC=；⑤PE BPPD CP=.其中不需要添加其他条件就能使△BPE∽△CPD的条件有____个，它们分别是____(填序号) .7．在△ABC和△DEF中，如果AB＝4，BC＝3，AC＝6；DE＝2.4，EF＝1.2，FD＝1.6，那么这两个三角形能否相似的结论是____________，理由是__________________．8．如图所示，△ABC的高AD，BE交于点F，则图中的相似三角形共有______对．9．如图所示，□ABCD中，G是BC延长线上的一点，AG与BD交于点E，与DC交于点F，此图中的相似三角形共有______对．三、解答题10.已知两直角三角形ABC 与ACD ，∠ACB=∠ADC=90°，6AC =，AD=2.问当AB 的长为多少时，这两个直角三角形相似.11.根据下列各组条件，判断ABC ∆和A B C '''∆是否相似，并说明理由.（1）AB=3.5，BC=2.5，CA=4，24.5A B ''=，17.5B C ''=，28C A ''=；（2）∠A=35°，∠B=104°，∠C=44°，35A '∠=︒；（3）AB=3，BC=2.6，∠B=48°， 1.5A B ''=， 1.3B C ''=，48B '∠=︒.12.已知线段0A 丄0B ，点C 为OB 的中点，点D 为AO 上一点，连接AC ，BD 交于点P.（1）如图①，当OA=OB 且点D 为AO 的中点时，求AP PC的值； （2）如图②，当OA=OB 且14AD AO =时，求AP AC 的值.13.如图，在ABC ∆和DEF ∆中，∠A=∠D=70°，∠B=50°，∠E=30°，分别过两个三角形的一个顶点画直线1，m ，使直线l 将ABC ∆分成两个小三角形，直线m 将DEF ∆分成两个小三角形，并使ABC ∆分成的两个小三角形分别与DEF ∆分成的两个小三角形相似，并标出每个小三角形各个内角的度数.（画图工具不限，不要求写作法，只需画出一种分法即可）参考答案1．D．2．A．3.B 解析：图中相似的三角形有△ABC∽△CDA，△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA，共5对.4.B解析：①④正确.5.C解析：②③④正确.6.4 ①②④⑤7．△ABC ∽△DFE ．因为这两个三角形中，三组对应边的比相等．8．6对．9．6对．10.分析:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.在Rt △ABC 和Rt △ACD 中，直角边的对应需分情况讨论.解: ∵ AD=2，∴CD =.要使 Rt △ABC 与 Rt △ACD 相似，有两种情况：(1)当 Rt △ABC ∽Rt △ACD 时，有AC AB AD AC=， ∴23AC AB AD==, (2)当 Rt △ACB ∽Rt △CDA 时，有AC AB CD AC=,∴AB=2AC CD=故当AB 的长为3或时，这两个直角三角形相似.点拨:本题考査相似三角形的判定.判定两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角，可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.11. 分析：（1)题中的条件全部是边长，因此验证三边是否成比例；(2)题中的条件全部是角，因此验证是否有两对对应角相等；(3)题中的条件既有边也有角，验证两边是否成比例且夹角相等.解：（1）因为3.51 2.5141,,''24.57''17.57''287AB BC CA A B B C C A ======， 所以''''''AB BC CA A B B C C A ==，所以△ABC ∽△A ＇B ＇C ＇. 理由：三组对应边成比例的两个三角形相似.(2) 在△ABC 中，因为∠A=35°, ∠B=104°，所以 ∠C=180°-∠A-∠B=180°-35°-104°=41°在△A ＇B ＇C ＇中，因为∠C ＇=44°, ∠A ＇=35°，所以∠B ＇= 180°-∠A ＇-∠C ＇ = 180°-35°-44°=101°.因为对应角不相等，所以△ABC 与△A ＇B ＇C ＇不相似.(3) 在 △ABC 与 △A ＇B ＇C ＇中∠B=∠B ＇= 48°，且''AB A B = 2，''BC B C = 2，所以''''AB BC A B B C =,所以 △ABC ∽△A ＇B ＇C ＇. 理由:对应边成比例且夹角相等的两个三角形相似.12. 解：（1)过点C 作CE//OA 交BD 于点E,则 △ABC ∽△BOD,. 得 CE= 12OD= 12AD. 再由△ECP ∽△DAP ，得23AP AD PC EC ==. (2)过点C 作CE//OA 交BD 于点E ，设AD=x ，则 AO=OB=4x ，OD=3x.由 △BCE ∽△BOD ，得 CE=12OD=32x ， 再由△ECP ∽△DAP ，得23AP AD PC EC ==，则25AP AC =. 13.解:如图(答案不唯一).则直线l ，m 即为所求作的直线.点拨：解答本题是从构造相等的角这一角度考虑的，当然也可以从构造比例线段出发，不过从这一角度考虑相对比较困难.。

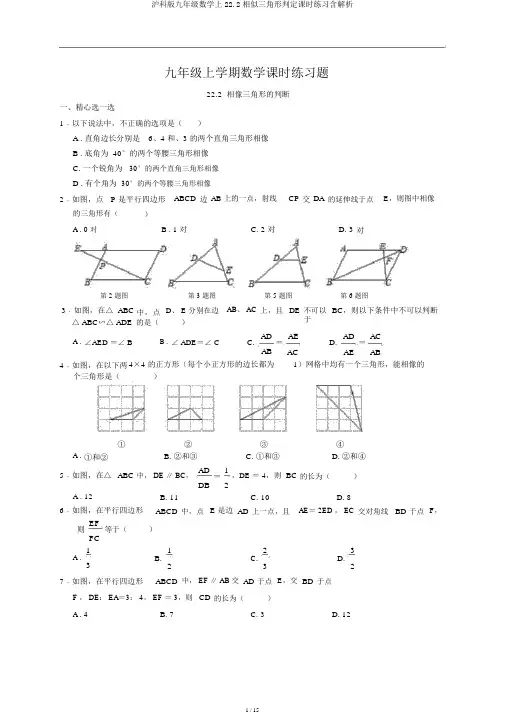
九年级上学期数学课时练习题22.2 相像三角形的判断一、精心选一选1﹒以下说法中，不正确的选项是（）A . 直角边长分别是6、4 和、3 的两个直角三角形相像B . 底角为 40°的两个等腰三角形相像C. 一个锐角为30°的两个直角三角形相像D . 有个角为30°的两个等腰三角形相像2﹒如图，点P 是平行四边形ABCD边AB 上的一点，射线CP交DA的延伸线于点E，则图中相像的三角形有（）A . 0 对B . 1 对 C. 2 对 D. 3对第 2 题图第 3 题图第 5 题图第 6 题图3﹒如图，在△ ABC △ ABC∽△ ADE 中，点的是（D、 E 分别在边）AB、 AC上，且DE不可以于BC，则以下条件中不可以判断A .∠AED ＝∠B B .∠ ADE＝∠C C.AD＝AED.AD＝AC AB AC AE AB4﹒如图，在以下两个三角形是（4×4 的正方形（每个小正方形的边长都为）1）网格中均有一个三角形，能相像的A .①和②①②B. ②和③③C. ①和③④D. ②和④5﹒如图，在△ABC中， DE ∥ BC，AD＝1，DE ＝ 4，则BC的长为（）DB2A . 12 B. 11 C. 10 D. 86﹒如图，在平行四边形ABCD中，点 E 是边AD上一点，且AE＝ 2ED ， EC交对角线BD于点F，则EF等于（）FC1123A . B. C. D.3232 7﹒如图，在平行四边形ABCD中， EF ∥ AB 交AD于点E，交BD于点F ， DE： EA＝3： 4， EF ＝ 3，则CD的长为（）A . 4 B. 7 C. 3 D. 12第 7 题图第 8 题图第 9 题图第 10 题图8﹒如图，在等腰梯形ABCD中， AD∥ BC，过点 C 作CE∥ AB， P 是梯形ABCD内一点，连结BP 并延伸交CD于点F，交CE 于点E，再连结PC.已知BP＝ PC，则以下结论错误的选项是（）A .∠1＝∠ 2 B. ∠ 2＝∠ E C. △PFC∽△ PCE D.△EFC ∽△ ECB9﹒如图，在△ ABC DEFG 是正方形中， AB ＝AC，点. 若 DE＝ 2cm，则D、 E 分别是AC 的长为（AB、 AC）的中点，点G、 F 在BC边上，四边形A . 3 3 cmB . 4cm C. 2 3 cm D. 2 5 cm10.如图，四边形 ABCD 中， AC 均分∠ DAB，∠ ADC ＝∠ ACB＝ 90°，点 E 为 AB 的中点，给出以下结论：① CE∥ AD ；② AC 2＝ AB AD ；③△ CDF ∽△ BCE；④ AC： AF＝ DE ：DF ，此中正确的有（）A . ①② B. ①②③ C. ①②④ D. ①②③④二、仔细填一填11. 如图，有以下条件：①∠B＝∠ C；②∠ ADB ＝∠ AEC；③ADAE ；④ AD AE ；AC AB AB AC⑤ PE BP，此中一个条件就能使△BPE∽△ CPD 的条件有 ___________ 个，它们分别是PD PC__________________. （只填写序号）第 11 题图第12题图第13题图12.如图，在边长为 1 的正方形网格中有点 P、 A、 B、 C，则图中所形成的三角形中，相像的三角形是 ______________________.13.如图，已知△ ABC 中， AB＝ 5， AC＝ 3，点 D 在边 AB 上，且∠ ACD＝∠ B，则线段 AD 的长为__________ .14.如图，点 D 为△ ABC 外一点， AD 与 BC 边的交点为 E，AE ＝3， DE＝ 5，BE＝ 4，要使△BDE ∽△ ACE ，且点 B， D 的对应点为A， C，那么线段CE 的长应等于 ________.第 14 题图第15题图第16题图15.如图，正方形 ABCD 中， E 为 AB 的中点， AF ⊥ DE 于点 O，则AO等于 __________.DO16.如图，在矩形 ABCD 中， AB＝6， BC＝ 8，沿直线 MN 对折，使 A， C 重合，直线 MN 交 AC 于点 O，则线段 OM ＝ ________.三、解答题17. 已知：如图，△ ABC 中，∠合），∠ ADE＝ 45°. 求证：△BAC＝ 90°， AB＝ AC，点ABD∽△ DCE.D是 BC边上的一个动点（不与B，C重18. 在平行四边形ABCD 中， E 为 BC 边上的一点，连结AE.（1）若 AB＝ AE，求证：∠ DAE ＝∠ D；（2）若点 E 为 BC 的中点，连结 BD ，交 AE 于 F ，求 EF ：FA 的值 .19.如图，在△ ABC 中， D 、E 分别是边 AB、 AC 的中点， F 为 CA 延伸线上一点，∠F ＝∠ C.（1）若 BC＝8，求 FD 的长；（2）若 AB＝ AC，求证：△ ADE ∽△ DFE .20.如图，在△ ABC 中， AB ＝AC，点 P、 D 分别是 BC、 AC 边上的点，且∠ APD ＝∠ B.（1）求证： AC CD ＝CP BP；（2）若 AB＝ 10， BC＝ 12，当 PD∥ AB 时，求 BP 的长 .21.已知：如图， E 是矩形 ABCD 的边 BC 上一点， EF ⊥ AE， EF 分别交 AC、 CD 于点M、F ， BG⊥ AC，垂足为 G， BG 交 AE 于点 H.（1）求证：△ ABE∽△ ECF ；（2）找出与△ ABH 相像的三角形，并加以证明；（3）若 E 是 BC 的中点， BC＝ 2AB， AB＝ 2，求 EM 的长 .22. 如图，正方形ABCD 中， M 为 BC 上一点， F 是 AM 的中点， EF⊥ AM ，垂足为 F，交 AD 的延伸线于点 E，交 DC 于点 N.（1）求证：△ ABM∽△ EFA ；（2）若 AB＝ 12， BM ＝ 5，求 DE 的长 .23.如图，在△ ABC 中， AB ＝8cm， BC＝ 16cm，点 P 从点 A 开始沿 AB 向点 B 以 2cm/s 的速度运动，点Q 从点 B 开始沿 BC 向点 C 以 4cm/s 的速度运动 . 假如 P、 Q 分别从 A、 B 同时出发， 4 秒后停止运动，则在开始运动后第几秒，△BPQ 与△ BAC 相像？《相像三角形的判断》课时练习题参照答案一、精心选一选题号12345678910答案D D C B A A B D D C1﹒以下说法中，不正确的选项是（A . 直角边长分别是6、4 和）、3 的两个直角三角形相像B . C.底角为 40°的两个等腰三角形相像一个锐角为30°的两个直角三角形相像D . 有个角为30°的两个等腰三角形相像解答： A. 直角边长分别是6、 4 和、 3 的两个直角三角形相像，由于两边对应成比率，且夹角相等，因此这两个直角三角形相像，故 A 正确；B. 底角为40°的两个等腰三角形相像，由于有两角对应相等，因此这两个等腰三角形相像，故 B 正确；C. 一个锐角为30°的两个直角三角形相像，由于有两角对应相等，因此这两个等腰三角形相像，故C正确；D.有个角为 30°的两个等腰三角形相像，由于可能一个角为极点，另一个为底角，因此这两个等腰三角形不相像，故 D 错误，应选： D.2﹒如图，点P 是平行四边形ABCD边AB 上的一点，射线CP交DA的延伸线于点E，则图中相像的三角形有（）A . 0 对B . 1 对 C. 2 对 D. 3对解答：∵四边形ABCD是平行四边形，∴AB∥DC， AD∥ BC，∴△ EAP ∽△ EDC，△ EAP∽△ CPB，∴△ EDC ∽△ CBP，故有 3 对相像三角形．应选： D．3﹒如图，在△ ABC 中，点 D、 E 分别在边AB、 AC 上，且 DE 不可以于 BC，则以下条件中不可以判断△ ABC∽△ ADE的是（）A .∠AED ＝∠B B .∠ADE ＝∠C C.AD＝AED.AD＝AC AB AC AE AB解答：∵∠ DAE＝∠ CAB，∴当∠ AED ＝∠ B 或∠ ADE ＝∠ C 时，△ ABC ∽△ ADE ，当AD＝AC时，△ ABC∽△ ADE，AE AB应选： C.4﹒如图，在以下两个三角形是（4×4 的正方形（每个小正方形的边长都为）1）网格中均有一个三角形，能相像的①② ③④A . ①与②B . ①与③C. ②与③D . ②与④解答： 由勾股定理可求出图①中三角形的各边长分别为 2， 2 ，10 ，图③中三角形的各边长分别为2 2 ， 2， 25 ，∵2 ＝ 2 ＝ 210 ， 2225∴图①中三角形与图③中三角形相像，应选： B.5﹒如图，在△ ABC 中， DE ∥ BC ，AD＝ 1，DE ＝ 4，则 BC 的长为（）DB 2A . 12B . 11C. 10D . 8解答： ∵AD＝ 1， AD+DB ＝ AB ，DB 2∴AD＝1，AB 3∵ DE ∥BC ，∴△ ADE ∽△ ABC ，∴DE＝AD ，即 4 ＝ 1，BCABBC 3解得： BC ＝ 12.应选： A.6﹒在平行四边形ABCD 中，点 E 是边 AD 上一点，且AE ＝ 2ED ，EC 交对角线 BD 于点 F ，则EF等于（）FC1 1 C.2 3 A . B .3D .322解答： ∵四边形 ABCD 是平行四边形，∴ ED ∥BC ， BC ＝ AD ， ∴△ DEF ∽△ BCF ，∴EF DE ， CF CB 设 ED ＝ k ，则 AE ＝ 2k ， BC ＝ 3k ，∴EFk1 ，CF3k3应选： A.7﹒如图，在平行四边形ABCD 中， EF ∥ AB 交 ADF ， DE ： EA ＝3： 4， EF ＝ 3，则 CD 的长为（于点）E ，交BD于点A . 4 B. 7 C. 3 D . 12解答：∵ DE： EA＝ 3： 4，∴DE ：DA ＝3：7，∵ EF ∥AB，∴DE EF ，DA AB∵EF ＝3，∴3 3，7 AB解得： AB＝ 7，∵四边形ABCD 是平行四边形，∴ CD＝ AB＝ 7，应选： B.8﹒如图，在等腰梯形ABCD 中， AD∥ BC，过点 C 作 CE∥ AB， P 是梯形 ABCD 内一点，连结BP 并延伸交CD 于点 F，交 CE 于点 E，再连结 PC. 已知 BP＝ PC，则以下结论错误的选项是（）A . ∠1＝∠ 2 B. ∠ 2＝∠ E C. △ PFC ∽△ PCE D . △EFC ∽△ ECB解答：∵四边形ABCD 是等腰梯形，∴∠ ABC ＝∠ DCB ，∵ PB＝PC，∴∠ PBC ＝∠ PCB，∴∠ ABC －∠ PBC＝∠ DCB －∠ PCB，∴∠ 1＝∠ 2，故 A 正确，∵CE∥AB，∴∠ 1＝∠ E，∴∠ 2＝∠ E，故 B 正确；∵∠ CPF ＝∠ EPC，∴△ PFC ∽△ PCE，故 C 正确；由已知条件不可以证明△EFC ∽△ ECB，应选： D.9﹒如图，在△ ABC 中， AB ＝AC，点 D、 E 分别是 AB、 AC 的中点，点 G、 F 在 BC 边上，四边形DEFG 是正方形 . 若 DE＝ 2cm，则 AC 的长为（）A . 3 3 cm B. 4cm C. 2 3 cm D. 2 5 cm解答：∵ E 是 AAC 的中点，∴AE1 ，AC2∵四边形 DEFG 是正方形，∴ DE ∥ BC，∴ DE AE ，∴ 2 1 ，BC ACBC2∴BC＝4cm，∵ AB＝AC，且四边形DEFG 是正方形，∴FC ＝1( 4－2) ＝ 1cm，2由勾股定理得：EC＝EF 2FC 2＝ 5 cm，∴ AC ＝2EC ＝ 2 5 cm ，应选 D .10. 如图，四边形 ABCD 中， AC 均分∠ DAB ，∠ ADC ＝∠ ACB ＝ 90°，点 E 为 AB 的中点，给出以下结论：① CE ∥ AD ；② AC 2＝ AB AD ；③△ CDF ∽△ BCE ；④ AC ： AF ＝ DE ：DF ，此中正确的 有（ ） A . ①② B . ①②③C. ①②④D. ①②③④解答： ∵∠ ACB ＝ 90°，点 E 为 AB 的中点，∴ AE ＝CE ＝BE ，∴∠ ACE ＝∠ BAC ， ∵∠ DAC ＝∠ BAC ， ∴∠ ACE ＝∠ DAC ，∴ CE ∥AD ，故①正确；∵∠ ADC ＝∠ ACB ＝ 90°，∠ DAC ＝∠ BAC ， ∴△ ADC ∽△ ACB ，∴AC AD，即 AC 2＝ AB AD ，故②正确；AB AC∵ CE ∥AD ， ∴ FC EF ，∴ FC AF EF DF ，AF DFAFDF∴AC DE，故④正确，AF DF∵△ CDF 与△ BCE 不具备相像的条件，∴③不正确， 应选： C.二、仔细填一填11. 4，①②④⑤；12. △APB ∽△ CPA ；13. 9 ；514. 15 ；15. 1 ；16. 15 ；42411. 如图，有以下条件：①∠B ＝∠C ；②∠ ADB ＝∠ AEC ；③ADAE ；④ ADAE ；AC ABABAC⑤ PEBP，此中一个条件就能使△ BPE ∽△ CPD 的条件有 ___________ 个，它们分别是PD PC__________________. （只填写序号） 解答： 使△ BPE ∽△ CPD 的条件有 4 个，∵∠ CPD ＝∠ BPE ，∠ B ＝∠ C ，∴△ BPE ∽△ CPD ，故①切合； ∵∠ ADB ＝∠ AEC ，∴∠ CDP ＝∠ BEP ，∵∠ CPD ＝∠ BPE ，∴△ BPE ∽△ CPD ，故②切合 ∵∠ A ＝∠ A ，ADAE ，ABAC∴△ ACE ∽△ ABD ，∴∠ ADB ＝∠ AEC ，∴∠ CDP ＝∠ BEP ，∵∠ CPD ＝∠ BPE ，∴△ BPE ∽△ CPD ，故④切合；∵∠ CPD ＝∠ BPE ， PE BP，PDPC∴△ BPE ∽△ CPD ，故⑤切合，故答案为： 4，①②④⑤.12. 如图，在边长为 1 的正方形网格中有点 P 、 A 、 B 、 C ，则图中所形成的三角形中，相像的三角形是 ______________________.解答： ∵ AP ＝ 5 ， PB ＝ 1， PC ＝ 5，∴ AP 5 ， PB1 5 ， PC5AP55∵∠ APB ＝∠ CPA ， ∴△ APB ∽△ CPA ，故答案为：△ APB ∽△ CPA.13. 如图，已知△ ABC 中， AB ＝ 5， AC ＝ 3，点 D 在边 AB 上，且∠ ACD ＝∠ B ，则线段 AD 的长为__________ .解答： ∵∠ A ＝∠ A ，∠ ACD ＝∠ B ，∴△ ABC ∽△ ACD ，∴AB AC ，AC AD∵ AB ＝5， AC ＝ 3， ∴53 ，∴ AD ＝ 9，3 AD 5故答案为：9．514. 如图，点 D 为△ ABC 外一点， AD 与 BC 边的交点为 E ，AE ＝3， DE ＝ 5，BE ＝ 4，要使△BDE ∽△ ACE ，且点 B ， D 的对应点为 A ， C ，那么线段 CE 的长应等于 ________. 解答： ∵∠ AEC ＝∠ BED ，∴当 BE DE 时，△ BDE ∽△ ACE ，AE CE即4 5，3 CE∴ CE ＝15，4故答案为：15．415. 如图，正方形 ABCD 中， E 为 AB 的中点， AF ⊥ DE 于点 O ，则 AO等于 __________.DO解答： ∵∠ ADO ＝∠ ADO ，∠ DOA ＝∠ DAE ＝90°， ∴△ AOD ∽△ EAD ，∴AO AE 1 ， DOAD 2故答案为：1.216. 如图，在矩形 ABCD 中， AB ＝6， BC ＝ 8，沿直线 MN 对折，使 A ， C 重合，直线 MN 交 AC 于点 O ，则线段 OM ＝ ________. 解答： 在 Rt △ABC 中， AB ＝ 6， BC ＝ 8， ∴ AC ＝10，∴ OC ＝ 5，∵ A 与 C 对于直线 MN 对称， ∴ AC ⊥MN ，∴∠ COM ＝ 90°，∵在矩形 ABCD 中，∠ B ＝90°，∴∠ COM ＝∠ B ＝ 90°， 又∵∠ MCO ＝∠ ACB ，∴△ COM ∽△ CBA ，∴OC OM ， BC AB∴ OM ＝15，4故答案为： 15.4三、解答题17. 已知：如图，△ ABC 中，∠ BAC ＝ 90°， AB ＝ AC ，点 合），∠ ADE ＝ 45°. 求证：△ ABD ∽△ DCE. 解答： ∵∠ BAC ＝ 90°， AB ＝ AC ， ∴∠ B ＝∠ C ＝ 45° ，∴∠ 1+ ∠ 2＝ 180° －∠ B ＝ 135°，∵∠ 2+ ∠ ADE+∠ 3＝ 180°，∠ ADE ＝45°，∴∠ 2+ ∠ 3＝ 180° －∠ ADE ＝ 135°，D 是 BC边上的一个动点（不与B ，C重∴∠ 1＝∠ 3，∴△ ABD ∽△ DCE .18. 在平行四边形 ABCD 中， E 为 BC 边上的一点，连结 AE.（ 1）若 AB ＝ AE ，求证：∠ DAE ＝∠ D ；（ 2）若点 E 为 BC 的中点，连结 BD ，交 AE 于 F ，求 EF ：FA 的值 . 解答： （ 1）在平行四边形 ABCD 中， AD ∥ BC ， ∴∠ AEB ＝∠ DAE ，∵ AE ＝AB ，∴∠ B ＝∠ AEB ， ∴∠ B ＝∠ DAE ， ∵∠ B ＝∠ D ， ∴∠ DAE ＝∠ D ；（ 2）∵四边形 ABCD 是平行四边形，∴ AD ∥BC ， AD ＝ BC ， ∴△ BEF ∽△ AFD ，∴EF BE ，FA AD∵ E 为 BC 的中点，∴ BE ＝ 1 BC ＝ 1AD ，即BE1 ，2 2AD2∴EF ：FA ＝1： 2．19.如图，在△ ABC 中， D 、E 分别是边 AB、 AC 的中点， F 为 CA 延伸线上一点，∠F ＝∠ C.（1）若 BC＝8，求 FD 的长；（2）若 AB＝ AC，求证：△ ADE ∽△ DFE .解答：（ 1）∵ D 、E 分别是边AB、 AC 的中点，∴DE ＝1BC＝ 4， DE∥ BC．2∴∠ AED ＝∠ C．∵∠ F ＝∠ C，∴∠ AED ＝∠ F ，∴FD ＝DE ＝ 4；（2）∵ AB＝ AC， DE ∥ BC．∴∠ B＝∠ C＝∠ AED ＝∠ ADE，∵∠ AED ＝∠ F ，∴∠ ADE ＝∠ F ，又∵∠ AED ＝∠ AED ，∴△ ADE ∽△ DFE ．20.如图，在△ ABC 中， AB ＝AC，点 P、 D 分别是 BC、 AC 边上的点，且∠ APD ＝∠ B.（1）求证： AC CD ＝CP BP；（2）若 AB＝ 10， BC＝ 12，当 PD∥ AB 时，求 BP 的长 .解答：（ 1）∵ AB＝ AC，∴∠ B＝∠ C，∵∠ APD ＝∠ B，∴∠ APD ＝∠ B＝∠ C，∵∠ APC ＝∠ BAP+∠ B，∠ APC＝∠ APD +∠ DPC ，∴∠ BAP ＝∠ DPC，∴△ ABP ∽△ PCD，∴BP AB ，CD CP∴AB CD ＝ CP BP ，∵ AB＝AC，∴AC CD＝ CP BP；（2）∵ PD ∥ AB，∴∠ APD ＝∠ BAP．∵∠ APD ＝∠ C，∴∠ BAP＝∠C．∵∠ B＝∠ B，∴△ BAP ∽△ BCA，∴BA BP ．BC BA∵ AB＝10， BC＝ 12，∴10BP，12 10∴ BP＝25 ．321.已知：如图， E 是矩形 ABCD 的边 BC 上一点， EF⊥ AE， EF 分别交 AC、CD 于点M 、F ， BG⊥ AC，垂足为 G， BG 交 AE 于点 H.（1）求证：△ ABE∽△ ECF ；（2）找出与△ ABH 相像的三角形，并加以证明；（ 3）若 E 是 BC 的中点， BC ＝ 2AB ， AB ＝ 2，求 EM 的长 . 解答： （ 1）∵四边形 ABCD 是矩形， ∴∠ ABE ＝∠ ECF ＝ 90°，∵ EF ⊥AE ，∴∠ AEB+∠FEC ＝ 90°， ∵∠ AEB +∠ BAE ＝90°，∴∠ BAE ＝∠ FEC ， ∴△ ABE ∽△ ECF ； （ 2）△ ABH ∽△ ECM ， ∵ BG ⊥AC ，∠ ABC ＝90°，∴∠ ABH +∠BAG ＝ 90°，∠ ECM +∠ BAG ＝ 90° ， ∴∠ ABH ＝∠ ECM ， 又∠ BAH ＝∠ CEM ， ∴△ ABH ∽△ ECM ； （ 3）作 MN ⊥ BC 于点 N ， ∵ AB ＝BE ＝EC ＝2， MN ∥AB ，∴ABMN1，∠ AEB ＝45°，BC NC2∴∠ MEN ＝ 45°， NC ＝ 2MN ， ∴ MN ＝ EN ＝ 1NC ，2∵ NC+EN ＝ EC ＝ 2，∴ MN ＝ EN ＝ 2× 1 ＝ 2， 3 3∴ EM 2＝ MN 2+EN 2＝ ( 2)2+( 2)2 ，33∴ EM ＝2 2.322. 如图，正方形 ABCD 中， M 为 BC 上一点， F 是 AM 的中点， EF ⊥ AM ，垂足为 F ，交 AD 的延伸线于点 E ，交 DC 于点 N.（ 1）求证：△ ABM ∽△ EFA ；（ 2）若 AB ＝ 12， BM ＝ 5，求 DE 的长 . 解答： （ 1）证明：∵四边形 ABCD 是正方形，∴ AB ＝AD ，∠ B ＝ 90°， AD ∥ BC ， ∴∠ AMB ＝∠ EAF ，又∵ EF ⊥ AM ， ∴∠ AFE ＝ 90°， ∴∠ B ＝∠ AFE ， ∴△ ABM ∽△ EFA ；（ 2）解：∵∠ B ＝ 90°，AB ＝12， BM ＝5，∴ AM ＝ 122 52 ＝13， AD ＝12，∵ F 是 AM 的中点，∴ AF ＝ 1AM ＝，2 ∵△ ABM ∽△ EFA ，∴BMAM，即 5 13 ，AFAEAE∴AE＝，∴DE ＝AE－ AD＝．23.如图，在△ ABC 中， AB ＝8cm， BC＝ 16cm，点 P 从点 A 开始沿点 Q 从点 B 开始沿 BC 向点 C 以 4cm/s 的速度运动 . 假如 P、 Q停止运动，则在开始运动后第几秒，△BPQ 与△ BAC 相像？解答：设在开始运动后第 x 秒，△ BPQ 与△ BAC 相像，由题意得： AP＝ 2xcm，PB ＝（ 8﹣ 2x）cm，BQ＝ 4x，分两种状况考虑：当∠ BPQ ＝∠ C，∠ B＝∠ B 时，△ PBQ ∽△ CBA，AB 向点 B 以 2cm/s 的速度运动，分别从 A、 B 同时出发， 4 秒后∴ BP BQ ，即 8 2 x 4 x ，BC AB168解得： x＝，当x＝ 0.8 秒时，△ BPQ 与△ BAC 相像；当∠ BPQ ＝∠ A，∠ B＝∠ B 时，△ BPQ ∽△ BAC，∴ BP BQ ，即 82x4x ，BA BC816解得： x＝ 2，当 x＝ 2 秒时，△ BPQ 与△ BAC 相像．综上，当x＝0.8 秒或 2 秒时，△ BPQ 与△ BAC 相像．。

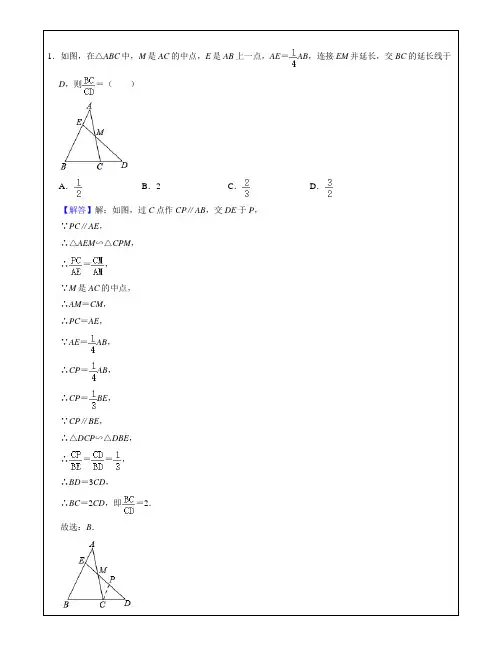
1．如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝（）A．B．2C．D．【解答】解：如图，过C点作CP∥AB，交DE于P，∵PC∥AE，∴△AEM∽△CPM，∴＝，∵M是AC的中点，∴AM＝CM，∴PC＝AE，∵AE＝AB，∴CP＝AB，∴CP＝BE，∵CP∥BE，∴△DCP∽△DBE，∴＝＝，∴BD＝3CD，∴BC＝2CD，即＝2．故选：B．2．如图，在△ABC中，点D在线段BC上，∠B＝∠DAC，AC＝8，BC＝16，那么CD（）A．4B．6C．8D．10【解答】解：∵∠B＝∠DAC，∠C＝∠C，∴△ABC∽△DAC，∴＝，∴AC2＝CD×BC，即82＝CD×16，解得：CD＝4；故选：A．【知识梳理1】比例线段平行线分线段成比例定理：三条平行线截两条直线，所得对应线段成比例。

推广：过一点的一线束被平行线截得的对应线段成比例。

定理推论：①平行于三角形一边的直线截其它两边（或两边的延长线）所得对应线段成比例。

②平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例。

【例题精讲】1．如图，用图中的数据不能组成的比例是（）A．2：4＝1.5：3B．3：1.5＝4：2C．2：3＝1.5：4D．1.5：2＝3：4【解答】解：A、2：4＝1：2＝1.5：3，能组成比例，错误；B、3：1.5＝2：1＝4：2，能组成比例，错误；C、2：3≠1.5：4；不能组成比例，正确；D、1.5：2＝3：4，能组成比例，错误；故选：C．2．如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．若AB＝4.5，BC ＝3，EF＝2，则DE的长度是（）A．2B．3C．5D．6【解答】解：∵AD∥BE∥CF，∴＝，∵AB＝4.5，BC＝3，EF＝2，∴＝，解得：DE＝3，故选：B．3．如图，AB∥CD∥EF，则下列结论正确的是（）A．B．C．＝D．【解答】解：∵AB∥CD∥EF，∴＝，＝，∴选项A、C、D不正确，选项B正确；故选：B．4．如图，已知直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E、B、D、F，AC＝4，CE＝6，BD ＝3，DF＝（）A．7B．7.5C．8D．4.5【解答】解：∵直线a∥b∥c，∴＝，即＝，∴DF＝．故选：D．5．如图，直线l1∥l2∥l3，直线AC分别交直线l1、l2、l3于点A、B、C，直线DF分别交直线l1、l2、l3于点D、E、F，直线AC、DF交于点P，则下列结论错误的是（）A．＝B．＝C．＝D．＝【解答】解：∵l1∥l2∥l3，∴＝，A正确，不符合题意；＝，B正确，不符合题意；＝，C错误，符合题意；＝＝，∴＝，D正确，不符合题意；故选：C．6．如图，在△ABC中，AD∥BC，点E在AB边上，EF∥BC，交AC边于点F，DE交AC边于点G，则下列结论中错误的是（）A．B．C．D．【解答】解：∵EF∥BC∴，∴答案A正确；根据合比性质，则有即：，∴答案D正确；又∵AD∥EF∴，∴答案B正确；而，∴答案C错误．故选：C．7．如图，如果l1∥l2∥l3，那么下列比例式中，错误的是（）A．B．C．D．【解答】解：∵l1∥l2∥l3，∴＝，＝，∴＝，故选：D．8．已知，在△ABC中，点D为AB上一点，过点D作DE∥BC，DH∥AC分别交AC、BC于点E、H，点F 是BC延长线上一点，连接FD交AC于点G，则下列结论中错误的是（）A．＝B．＝C．＝D．＝【解答】解：∵DE∥BC，DH∥AC，∴四边形DECH是平行四边形，∴DH＝CE，DE＝CH，∵DE∥BC，∴＝＝，故选项A正确，不符合题意，∵DH∥CG，∴＝＝，故C正确，不符合题意，∵DE∥BC，∴＝，∴＝，故D正确，不符合题意，故选：B．【课堂练习】1．如图，已知l3∥l4∥l5，它们依次交直线l1、l2于点E、A、C和点D、A、B，如果AD＝2，AE＝3，AB＝4，那么CE＝（）A．6B．C．9D．【解答】解：∵l3∥l4∥l5，∴＝，即＝，解得，AC＝6，则CE＝AE+AC＝9，故选：C．2．如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（）A．B．C．D．【解答】解：A、由AB∥CD∥EF，则，所以A选项的结论正确；B、由AB∥CD∥EF，则，所以B选项的结论正确；C、由AB∥CD∥EF，则，所以C选项的结论正确；D、由AB∥CD∥EF，则，所以D选项的结论错误；故选：D．3．如图所示，已知AB∥CD∥EF，那么下列结论正确的是（）A．＝B．＝C．＝D．＝【解答】解：∵AB∥CD∥EF，∴，∴A选项正确，故选：A．4．如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB＝3：5，那么CF：FB＝（）A．5：8B．3：8C．3：5D．5：3【解答】解：∵AD：DB＝3：5，∴BD：AB＝5：8，∵DE∥BC，∴CE：AC＝BD：AB＝5：8，∵EF∥AB，∴CF：CB＝CE：AC＝5：8．∴CF：FB＝5：3，故选：D．5．如图，l1∥l2，AF：FB＝3：5，BC：CD＝3：2，则AE：EC＝（）A．5：2B．4：3C．2：1D．3：2【解答】解：∵l1∥l2，∴＝＝，设AG＝3x，BD＝5x，∵BC：CD＝3：2，∴CD＝BD＝2x，∵AG∥CD，∴＝＝＝．故选：D．6．如图，在△ABC中，点D在BC边上，连接AD，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（）A．＝B．＝C．＝D．＝【解答】解：∵GE∥BD，GF∥AC，∴＝，＝，∴＝．故选：D．7．如图，l1∥l2∥l3，AC、DF交于点O，则下列比例中成立的是（）A．B．C．D．【解答】解：A、∵l1∥l2∥l3，∴，正确；B、∵l1∥l2∥l3，∴，错误；C、∵l1∥l2∥l3，∴，错误；D、∵l1∥l2∥l3，∴，错误；故选：A．8．如图，若l1∥l2∥l3，则下列各式错误的是（）A．B．C．D．【解答】解：∵l1∥l2∥l3，∴，，，故选：D．【知识梳理2】相似三角形的性质和判定相似三角形的性质：(1)对应角相等；(2)对应边成比例；(3)相似三角形的周长比等于相似比；(4)相似三角形的面积比等于相似比的平方。

24.4 相似三角形的判定同步测试一、选择题1. 下列判断中正确的是( ).A.全等三角形不一定是相似三角形B.不全等的三角形一定不是相似三角形C.不相似的三角形一定不全等D.相似三角形一定不是全等三角形2．已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′相似, 那么△A′B′C′的第三边长应该是 ( ).A. B. C. D.3．如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．4. 如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有（）A．0个B．1个C．2个D．3个5．在矩形ABCD中，E、F分别是CD、BC上的点，若∠AEF＝90°，则一定有（）.A．ΔADE∽ΔAEF B．ΔECF∽ΔAEF C．ΔADE∽ΔECF D．ΔAEF∽ΔABF6. 如图所示在平行四边形ABCD中，EF∥AB，DE：EA=2：3，EF=4，则CD的长为( ).A. B.8 C.10 D.16二、填空题7.如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是．（只需写一个条件，不添加辅助线和字母）8如图所示，∠C=∠E=90°，AD=10，DE=8，AB=5，则AC=________.9.如图所示，在直角坐标系中有两点A(4，0)，B(0，2)，如果点C在x轴上(C与A不重合)，当点C 的坐标为________或________时，使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10.如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB=__________.11.如图，CD∥AB，AC、BD相交于点O,点E、F分别在AC、BD上，且EF∥AB,则图中与△OEF相似的三角形为_________.12．如图，点E是平行四边形ABCD的边BC延长线上一点，连接AE交CD于点F,则图中相似三角形共有_________对.三．解答题13. 如图，在△ABC中，DE∥BC，AD＝3，AE＝2，BD＝4，求的值及AC、EC的长度．14. 如图在梯形ABCD中，AD∥BC，∠A＝90°，且，求证：BD⊥CD．15.如图，△ABC是等边三角形，点D、E分别在BC、AC上，且BD＝CE，AD与BE相交于点F．（1）试说明△ABD≌△BCE；（2）△EAF与△EBA相似吗？说说你的理由．16.如图，在△ABC中，已知∠BAC=90°，AD⊥BC于D，E是AB上一点，AF⊥CE于F，AD交CE 于G点，（1）求证：AC2=CE•CF；（2）若∠B=38°，求∠CFD的度数．答案与解析一．选择题1.【答案】C.2.【答案】A.【解析】根据三边对应成比例，可以确定3==226第三边，所以第三边是3.【答案】B.【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、只有选项B的各边为1、、与它的各边对应成比例．故选B．4.【答案】C．【解析】∵四边形ABCD是平行四边形，∴AD∥BC，AB∥DC，∴△AEF∽△CBF，△AEF∽△DEC，∴与△AEF相似的三角形有2个．5.【答案】C.【解析】∵∠AEF＝90°, ∴∠1+∠2=90°，又∵∠D=∠C=90°，∴∠3+∠2=90°，即∠1=∠3，∴△ADE∽△ECF.6.【答案】C.【解析】∵ EF∥AB，∴，∵，∴，，∴ CD=10，故选C.二. 填空题7.【答案】AB∥DE．【解析】∵∠A=∠D，∴当∠B=∠DEF时，△ABC∽△DEF，∵AB∥DE时，∠B=∠DEF，∴添加AB∥DE时，使△ABC∽△DEF．8.【答案】 3 .【解析】∵∠C=∠E，∠CAB=∠EAD，∴△ACB∽△AED，∴，BC=4，在Rt△ABC中，.9．【答案】；.10.【答案】4.【解析】∵AB⊥BD，ED⊥BD，∴∠B=∠D=90°，又∵AC⊥CE，∴∠BCA+∠DCE=90°，∴∠BCA=∠E,∴△ABC∽△CDE.∵C是线段BD的中点，ED=1，BD=4∴BC=CD=2∴AB CDCD DE,即AB=4.11.【答案】△OAB,△OCD.12.【答案】3.【解析】∵平行四边形ABCD，∴AD∥BE.AB∥CD∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.三综合题13.【解析】∵DE∥BC，∴△ADE∽△ABC，∵，，∴，∴AC＝，∴EC＝AC－AE＝．14.【解析】∵AD∥BC，∴∠ADB＝∠DBC，又∵，∴△ABD∽△DCB，∴∠A＝∠BDC，∵∠A＝90°，∴∠BDC＝90°，∴BD⊥CD ．15.【解析】（1）∵△ABC是等边三角形，∴AB＝BC，∠ABD＝∠BCE＝∠BAC，又∵BD＝CE，∴△ABD≌△BCE；（2）相似；∵△ABD≌△BCE，∴∠BAD＝∠CBE，∴∠BAC－∠BAD＝∠CBA－∠CBE，∴∠EAF＝∠EBA，又∵∠AEF＝∠BEA，∴△EAF∽△EBA．16.【解析】解：（1）∵AD⊥BC，∴∠CFA=90°，∵∠BAC=90°，∴∠CFA=∠BAC，∵∠ACF=∠FCA，∴△CAF∽△CEA，∴=，∴CA2=CE•CF；（2）∵∠CAB=∠CDA，∠ACD=∠BCA，∴△CAD∽△CBA，∴=，∴CA2=CB×CD，同理可得：CA2=CF×CE，∴CD•BC=CF•CE，∴=，∵∠DCF=∠ECB，∴△CDF∽△CEB，∴∠CFD=∠B，∵∠B=38°，∴∠CFD=38°．。

相似三角形的判定课前测试【题目】课前测试如图，已知CD 是△ABC 的高，D E⊥CA，DF⊥CB，求证：△CEF ∽△CBA.【答案】见解析 【解析】证明：∵CD ⊥AB，即∠CDA=∠CDB=90°，则∠A+∠ACD=90°， 又∵DE⊥CA，∴∠ACD+∠CDE=90°， ∴∠A=∠CDE，又∠ACD=∠DCE，∴△CAD ∽△CDE ，则CECDCD CA =，即CD 2=CA ·CE 同理可得△CBD ∽△CDF ，则CFCDCD CB =，即CD 2=CD 2=CB ·CF ∴CA ·CE=CB ·CF ，又∠ECF=∠BCA ，∴△CEF ∽△CBA总结：本题考察学生是否掌握“母子三角形”相似模型，待证的两个三角形中有一组公共角，因而再找出一组对应角相等或者是其夹角的两边成比例，经过分析发现，从角度入手基本不可能找出对应角相等，因而需要从夹角的两边证明. 该题属于典型的“母子三角形”模型，给出众多垂直关系，应该想到利用角度互余找等量. 只要“心中有模型”，对于这类题型的证明还是比较容易的. 【难度】3CAEDFB【题目】课前测试已知：如图，在ABC △中，AB AC =，M 是边BC 的中点，DME B ∠=∠，MD 与射线BA相交于点D ，ME 与边AC 相交于点E . （1）求证：BD CMDM EM=； （2）如果DE ME =，求证：//ME AB ；（3）在第（2）小题的条件下，如果DM AC ⊥，求ABC ∠的度数. 【答案】（1）证明：∵∠DMC=∠B+∠BDM ，∠DMC=∠DME+∠EMC ，∠DME=∠B ， ∴∠BDM=∠EMC ，∵AB=AC ，∴∠B=∠C ，∴△BDM ∽△CME ，EM DM CM BD =,即EMCMDM BD = （2）证明：∵△BDM ∽△CME,∴EC EMBM DM =， ∵DE=ME ，BM=CM ，∴ECDECM DM =，∠DME=∠EDM ， ∵∠DME=∠B=∠C ，∴∠EDM=∠C ，∴△DME ∽△CME ， ∴∠EMC=∠EMD ，∴∠EMD=∠B ，∴EM//AB ； （3）30° 【解析】（1）证明：∵∠DMC=∠B+∠BDM ，∠DMC=∠DME+∠EMC ，∠DME=∠B ， ∴∠BDM=∠EMC ，∵AB=AC ，∴∠B=∠C ，∴△BDM ∽△CME ，EMDMCM BD =,即EMCMDM BD = （2）证明：∵△BDM ∽△CME,∴ECEMBM DM =， （第24题图）EMCBAD适用范围：各版本，初三年级知识点概述：相似三角形作为中学阶段最重要的知识点之一，既是中考重点，也是难点. 重点是灵活运用相似三角形的各个判定定理，难点是相似三角形与分类讨论及函数思想的互相结合. 本讲义主要讲解相似三角形相关的判定定理以及几个常见的基本相似模型，学生在学习过程中务必理解熟记每个相似模型，能够在已知题干中发现并证明三角形相似.适用对象：中等成绩及偏上注意事项：相似三角形判定定理的学习应该牢牢掌握不同模型之间的区别，此外，在平时的学习过程中还应该多积累不同题型的解题思路. 对于这一部分的学习，基础中等的学生应该掌握几种常见的相似模型，能够结合图形和已知条件进行分析证明，基础较好的学生应该培养分类讨论思想以及数形结合的思想，逐渐熟悉综合性大题的解题思路.重点选讲：①相似三角形之一线三等角模型；②相似三角形之母子三角形模型；③相似三角形之公共边角模型；④相似三角形的综合应用知识梳理1：相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三边对应成比例，那么这两个三角形叫做相似三角形.说明：（1）相似三角形的定义虽然可以用来判断三角形相似，但是要求角与边的条件同时都满足的情况下才能使用；（2）相似三角形的书写具有严格的顺序性，不同的顺序代表不同的含义；（3）将两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数）；（4）如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似.知识梳理2：相似三角形的判定定理相似三角形的预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似.相似三角形判定定理1：如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似. 可简述为：两角对应相等，两个三角形相似.相似三角形的判定定理2：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似. 可简述为：两边对应成比例且夹角相等，两个三角形相似.相似三角形判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似. 可简述为：三边对应成比例，两个三角形相似.直角三角形相似的判定定理：如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例，那么这两个直角三角形相似. 可简述为：斜边和直角边对应成比例，两个直角三角形相似.强调：（1）有平行线时，用预备定理；（2）已有一对对应角相等(包括隐含的公共角或对顶角)时，可考虑利用判定定理1或判定定理2；（3）已有两边对应成比例时，可考虑利用判定定理2或判定定理3，但是在选择利用判定定理2时，一对对应角相等必须是成比例两边的夹角对应相等.知识梳理3：全等三角形与相似三角形判定定理比较知识梳理4：相似三角形基本相似模型的认识三角形全等三角形相似两角夹一边对应相等(ASA) 两角及一对边对应相等(AAS) 两边及夹角对应相等(SAS)三边对应相等(SSS) 直角边与斜边对应相等(HL) 两角对应相等两边对应成比例，且夹角相等三边对应成比例 直角边与斜边对应成比例基本相似模型有：公共边角型（A 字型、斜A 型、8字型、斜8型）、母子型、一线三等角等例题精讲【题目】题型1：相似三角形之一线三等角模型如图，已知在梯形ABCD 中，AD // BC ，90A ∠=︒，AB = AD ．点E 在边AB 上，且DE CD ⊥，DF 平分EDC ∠，交BC 于点F ，联结CE 、EF.（1）求证：DE = DC ；（2）如果BE 2=BF ·BC ，求证：BEF CEF ∠=∠. 【答案】见解析【解析】（1）作CH AD ⊥的延长线于点H ， ∵AD // BC ，90A ∠=︒，AB = AD ，∴CH AD =，∵DE CD ⊥，∴ADE HCD ∠=∠， ∴ADE ∆≌HCD ∆，∴DE DC =； （2）∵BE 2=BF ·BC ，B B ∠=∠， ∴BEF ∆∽BCE ∆，∴BEF BCE ∠=∠， ∵DF 平分EDC ∠，DE DC =， ∴DEF ∆≌DCF ∆，∴DEF DCF ∠=∠， ∵DEC DCE ∠=∠，∴CEF BCE ∠=∠，∴BEF CEF ∠=∠.总结：本题考查了 “一线三直角”模型及相似和全等三角形的综合应用，通过已知条件构造一线三等角，可以实现快速解题的效果. 【难度】4A BCDEFA BCDEFH【题目】题型1变式练习1相似三角形之一线三等角模型等腰△ABC，AB=AC=8，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转.（1）如图a，当三角板的两边分别交AB、AC于点E、F时. 求证：△BPE∽△CFP；（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC 于点E、F.①探究1：△BPE与△CFP还相似吗？（只需写出结论）②探究2：连接EF，△BPE与△PFE是否相似？请说明理由；；【答案】见解析【解析】（1）证明：∵在△ABC中，∠BAC=120°，AB=AC，∴∠B=∠C=30°，∵∠B+∠BPE+∠BEP=180°，∴∠BPE+∠BEP=150°，又∠EPF=30°，且∠BPE+∠EPF+∠CPF=180°，∴∠BPE+∠CPF=150°，∴∠BEP=∠CPF，∴△BPE∽△CFP（两角对应相等的两个三角形相似）．（2）解：①△BPE∽△CFP；②△BPE与△PFE相似．下面证明结论：同（1），可证△BPE∽△CFP，得CP/BE=PF/PE，又CP=BP，∴BP/PF=BE/PE,∵∠EBP=∠EPF ，∴△BPE ∽△PFE总结：“一线三等角”模型经常出现在等腰三角形、等边三角形、正方形、等腰梯形等几何图形中，因而当题干中出现以上图形时应当注意，有时候当题干给出了一条直线/线段上有两个角相等时，可以考虑构造第三个等角，利用“一线三等角”相似模型进行求解，如上题型1所示. 【难度】4【题目】题型1变式练习2相似三角形之一线三等角模型如图（1），在△ABC 中， AB=AC=5，BC=8，点P 、Q 分别在射线CB ，AC 上（点P 不与点C ，B 重合），且保持∠APQ=∠ABC.（1）若点P 在线段CB 上，且BP=6，求线段CQ 的长；（2）若BP=x ，CQ=y ，求y 与x 之间的函数关系式，并写出函数的定义域；（3）正方形ABCD 的长为5，如图（2），点P ，Q 分别在直线CB ，DC 上（点P 不与点C ，B 重合），且保持∠APQ=90°. 当CQ=1时，求出线段BP 的长. 【答案】 （1）125；（2）P 在BC 线段上：y=1(8)5x x -（0<x<8）；P 在BC 的延长线上：y=1(8)5x x +（x ≥8）； （3）当P 在线段BC 上，BP=552+或BP=552-；当P 在BC 的延长线上，PB=5352+ （2）（1）ABCDABPQ CQP【解析】（1）∵∠APQ+∠CPQ=∠B+∠BAP，∠APQ=∠ABC，∴∠BAP=∠CQP，又∵AB=AC，∴∠B=∠C，∴△CPQ∽△BAP．∴CQ CP BP AB=，∵AB=AC=5，BC=8，BP=6，CP=8-6=2，∴265CQ=∴CQ=125（2）若点P在线段CB上，由（1）知CQ CP BP AB=，∵BP=x，BC=8，∴CP=BC-BP=8-x，又∵CQ=y，AB=5，∴85y xx-=即y=1(8)5x x-，故所求的函数关系式为y＝1(8)5x x-（0＜x＜8）．若点P在线段CB的延长线上，如图．∵∠APQ=∠APB+∠CPQ，∠ABC=∠APB+∠PAB，∠APQ=∠ABC，∴∠CPQ=∠PAB，又∵∠ABP=180°-∠ABC，∠PCQ=180°-∠ACB，∠ABC=∠ACB，∴∠ABP=∠PCQ．∴△QCP∽△PBA．∴CQ CP BP AB=，∵BP=x，CP=BC+BP=8+x，AB=5，CQ=y，∴85y xx+=∴函数解析式为y=1(8)5x x+（x≥8）.（3）①当点P在线段BC上，∵∠APQ=90°，∴∠APB+∠QPC=90°，∵∠PAB+∠APB=90°，∴∠PAB=∠QPC，∵∠B=∠C=90°，∴△ABP∽△PCQ，∴AB：PC=BP：CQ，即5：（5-BP）=BP：1，ABCDEF解得：BP ＝552+或BP=552- ②当点P 在线段BC 的延长线上，则点Q 在线段DC 的延长线上， 同理可得：△ABP ∽△PCQ ，∴AB ：PC=BP ：CQ ，∴5：（BP-5）=BP ：1， 解得：BP ＝5352+或BP=5352-（舍）总结：本题考查一线三等角模型的相似问题，注意根据点的位置关系进行相应的讨论，属于模拟题以及中考真题中的常考压轴题型，这类题型的综合性一般较强，学生在平时的学习过程中应该养成良好习惯，培养分类讨论的思想. 【难度】5【题目】题型2：相似三角形之母子三角形模型在Rt ABC ∆中，90ACB ∠=︒，CD AB ⊥于点D ，E 是AC 边上的一个动点（不与A 、C 重合），CF BE ⊥于点F ，连接DF.（1）求证：CB 2=BF ·BE ； （2）求证： BF ·AE=FD ·BA【答案】见解析 【解析】ABCDE 证明：（1）90ACB ∠=，CF BE ⊥， ∴90ACB CFB ∠=∠=，又CBF CBE ∠=∠，∴CBF EBC ∆∆∽，∴CB BEBF CB=，∴CB 2=BF ·BE （2）90ACB ∠=，CD BA ⊥， ∴90ACB CDB ∠=∠=，又CBD CBA ∠=∠， ∴CBD ABC ∆∆∽， ∴CB ABBD CB=，即CB 2=BD ·BA ， ∴BF ·BE=BD ·BA ， ∴FB BDBA BE= ，又ABE FBD ∠=∠， ∴FBD ABE ∆∆∽，∴FB FDBA AE=，∴ BF ·AE=FD ·BA 总结:本题考查了三角形相似的判定定理与性质定理，当题干中出现较多垂直、直角时，可以考虑利用母子三角形模型证明三角形相似进行求解. 【难度】4【题目】题型2变式练习1：相似三角形之母子三角形模型如图，90ACB CED ∠=∠=︒，CD AB ⊥于点D ，3AC =，4BC =，求ED 的长. 【答案】3625【解析】3AC =，4BC =，=90ACB ∠︒，225AB AC BC ∴=+=，根据面积法，可知CD AB AC BC ⋅=⋅，解得125CD =， 又CD AB ⊥，=90ACB ∠︒，可得ADC ∆∽ACB ∆， AD AC AC AB ∴=， 代入可得：95AD =，90ACB CED ∠=∠=︒，//DE BC ∴，925DE AD BC AB ∴==， 代入得：3625ED =总结：考查对于“母子三角形”的认识，初步建立可将相似三角形中对应边之比转化为同一三角形中边长比的思想，实际上这个图形中包含5个直角三角形，全部都是两两相似. 【难度】3【题目】题型2变式练习2：相似三角形之母子三角形模型在矩形ABCD 中，点E 是AD 的中点，BE 垂直AC 交AC 于点F ，求证： （1）=；（2）∠EFD=∠DBC【答案】见解析 【解析】证明：（1）∵AC ⊥BE ，∴∠AFB=∠AFE=90°，∵四边形ABCD 是矩形，∴∠BAE=90°，∴∠AFE=∠BAE ， 又∵∠AEF=∠BEA ，∴△AEF ∽△BEA ， ∴=（2）∵点E 是AD 的中点，∴AE=ED ，∴=，又∵∠FED=∠DEB ， ∴△DEF ∽△EBD ， ∴∠EFD=∠EDB ， ∵AD//BC ， ∴∠DBC=∠EDB ， ∴∠EFD=∠DBC .总结：本题（1）利用母子三角形模型比较容易证明，第（2）问通常可以使用（1）中的结论进行命题的证明，属于比较常规的证明题. 【难度】3【题目】题型3：相似三角形之公共边角模型四边形ABCD 的对角线AC 与BD 相交于点E ： （1）若4=EA ，5=EB ，6.1=ED ，2=EC ，求证△EAD 与△EBC 是相似三角形；（2）若∠ABE=∠DCE ，求证AD ·CE=BC ·DE.【答案】见解析 【解析】 （1）∵54EC DE EB EA ==，又∠AED=∠BEC ，∴△EAD ∽△EBC（2）AD 、DE 在△AED 中，BC 、CE 在△BEC 中，即证△EAD ∽△EBC ∵在△ABE 与△DCE 中，∠ABE=∠DCE ，∠AEB=∠DEC ∴△ABE ∽△DCE ，则ECBEDE AE =，又∠AED=∠BEC ∴△EAD ∽△EBC ，即AD ·CE=BC ·DE总结：本题中（2）中的两个相似三角形符合“斜8字”模型，这类模型通常会有一对对顶角，然后再给出一组非内错角相等，通过相似三角形判定定理1即可得证. 对于求证四条线段之间的比例关系，一般按照先定、后找、再证的顺序进行分析，先确定四条线段在哪两个可能相似的三角形中；再找出两个三角形相似所需的条件；最后根据分析，写出证明过程. 【难度】3BA BCDEF 【题目】题型3变式练习1：相似三角形之公共边角模型如图，已知等腰三角形ABC 中，AB = AC ，高AD ，BE 相交于点H. 求证： 4DH ·DA=BC 2【答案】见解析 【解析】 证明：AD 、BE 是高， ∴90ADB BEC ∠=∠=，∴90HBD C ∠+∠=， 90CAH C ∠+∠=，∴HBD CAH ∠=∠， ∴HBD CAD ∆∆∽，∴HD BDCD AD=， 即DH ·AD=BD ·CD ， AB AC AD BC =⊥，， ∴12BD DC BC ==， ∴214DH AD BC =， ∴24DH AD BC =． 总结：本题考查“公共边角”模型，该题中一对直角三角形中不仅出现公共角，还出现了一对对顶角，这些元素很容易证明相应三角形的相似关系，再利用等腰三角形三线合一这一特点即可证明问题. 【难度】3【题目】题型3变式练习2：相似三角形之公共边角模型如图，梯形ABCD 中，AD // BC ，AB = DC ，对角线AC 、BD 相交于点F ，点E 是边BC 延长线上一点，且CDE ABD ∠=∠． （1）求证：四边形ACED 是平行四边形； （2）联结AE ，交BD 于点G ，求证：DG DFGB DB=ABCDE H【答案】见解析【解析】证明：（1）AD // BC，AB = DC，BAD CDA∴∠=∠，AB DC AD AD==，，ABD DCA∴∆≅∆，ACD ABD∴∠=∠，CDE ABD∠=∠，ACD CDE∴∠=∠，∴AC//DE，AD // BC，∴四边形ACED是平行四边形．（2）//AD BC，∴AD DFBC FB=，AD DFBC AD DF FB∴=++，四边形ACED是平行四边形，∴AD CE=，∴AD DFBC CE DF FB=++，即AD DFBE DB=，//AD BE，∴DG ADGB BE=，∴DG DFGB DB=.总结：考查相似中有平行线的情况，即可直接利用图形中的“A”字型和“8”字型等基本图形进行等比例转化，【难度】3【题目】题型4：相似三角形的综合应用如图，将边长为6 cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，则EBG∆的周长为______cm.【答案】见解析【解析】设DF x=，根据翻折的性质，则有EF x=，6AF x=-，在Rt AEF∆中，用勾股定理，则有222AE AF EF+=，即()22236x x+-=，解得154x=，则94AF=，由90A∠=︒，则有90AFE AEF∠+∠=︒，AB CDEFG HQMNH G FED CBA同时90FEG D ∠=∠=︒，则90AEF EBG ∠+∠=︒，得：AFE BEG ∠=∠，由90A B ∠=∠=︒，可证AEF ∆∽BGE ∆，则AE AF EFBG BE GE==，即9153443BG GE==，解得4BG =，5EG =，故12EBG C cm ∆=． 总结： 本题属于“一线三直角”基本模型，结合翻折、勾股定理相关知识点进行考查，是模拟题中常考题型，一般找出相似三角形，通过线段之间的比例关系列出等式求解，有时还会用到勾股定理或者锐角三角比等. 【难度】4【题目】题型4变式练习1：相似三角形的综合应用如图，点E 是矩形ABCD 的边BC 上一点，EF ⊥AE ，EF 分别交AC 、CD 于点M 、F ，BG ⊥AC ，垂足为点G ，BG 交AE 于点H.（1）求证：ABE ∆∽ECF ∆；（2）找出与ABH ∆相似的三角形，并证明；（3）若E 是BC 的中点，BC = 2AB ，AB = 2，求EM 的长.【答案】（1）见解析；（2）ECM ∆；（3）223【解析】（1）证明：EF AE ⊥，90AEB FEC ∴∠+∠=︒．90ABC ∠=︒ 90AEB BAE ∴∠+∠=︒ BAE FEC ∴∠=∠ 90ABE ECF ∠=∠=︒ ∴ABE ∆∽ECF ∆（2）由（1）BAE FEC ∠=∠，又90ABG GBC GBC BCG ∠+∠=∠+∠=︒ABG ECM ∴∠=∠ ，∴ABH ∆∽ECM ∆（3）作MN BC ⊥交BC 于点N ，则有//MN AB ，由BC = 2AB ，得2CN MN =， 2BC AB BE CE ==，45AB BE AEB FEC ∴=∠=∠=︒，12EN MN CN ∴==，得1233EN EC ==，则2223EM EN ==． 总结：该题涉及了“一线三等角”模型、“ 母子三角形”模型，一般而言，在这些模型中需要从角度入手，通过等量代换达到相似的目的，而在第二问中，往往需要第一问求出的相似，得出对应边或者对应角相等. 【难度】4【题目】题型4变式练习2：相似三角形的综合应用已知：正方形ABCD 的边长为4，点E 为BC 边的中点，点P 为AB 边上一动点，沿PE 翻折得到FPE ∆，直线PF 交CD 边于点Q ，交直线AD 于点G.（1）如图，当BP = 1.5时，求CQ 的长；（2）如图，当点G 在射线AD 上时，设BP = x ，DG = y ，求y 关于x 的函数关系式，并写出x 的取值范围； （3）延长EF 交直线AD 于点H ，若CQE ∆∽FHG ∆，求BP 的长.【答案】（1）83；（2）()21616124x y x x -=<<-；（3）233或23 【解析】 （1）连结QE ，ABCD EF GP QABCD EFGP Q290BE EF CE QE QE QFE C ====∠=∠=︒，，， QFE QCE ∴∆≅∆， 12FEQ CEQ FEC ∴∠=∠=∠，()1902PEQ BEF FEC ∴∠=∠+∠=︒， BPE QEC ∴∠=∠， BPE ∴∆∽CEQ ∆， BP BE CE CQ ∴=，即1.522CQ =，解得：83CQ =． （2）由（1）可得：BPE ∆∽CEQ ∆，由BP x =，可得：4CQ x =，则44DQ x=-，4AP x =-， 由//AB CD ，则有DQ GD AP GA=， 即4444y x x y -=-+，整理，得：()21616124x y x x -=<<-． （3）由题意知，90C GFH ∠=︒=∠，①G 在线段AD 的延长线上时，由CQE ∆∽FHG ∆，可知G CQE ∠=∠， CQE FQE ∠=∠，2DQG FQC G ∴∠=∠=∠， 90DQG G ∠+∠=︒，30G BEP ∴∠=︒=∠，BP ∴==， ②G 在线段AD 的反向延长线上时，同理可得：30G BPE ∠=︒=∠，BP ∴==总结：考查翻折与全等、相似等知识点，本题中出现了“母子三角形”比较隐蔽，需要一定的分析才能发现，第二问中出现了“A 字”型模型，通过表示出不同线段的长度，列出比例式即可求解，第三问考察分类讨论的思想，在平时的模拟考中比较常见，需要学生养成良好的解题习惯. 【难度】5【题目】兴趣篇1如图，在直角梯形ABCD 中，AB // CD ，AB ⊥BC ，对角线AC ⊥BD ，垂足为E ，AD=BD ，过E 的直线EF // AB 交AD 于点F.（1）AF = BE ； （2）AF 2 = AE ·EC【答案】见解析 【解析】（1）EF// AB ，AF 不平行EB ，∴四边形FABE 是梯形，又AD BD =， ∴DAB DBA ∠=∠，∴四边形FABE 是等腰梯形， ∴AF BE =；（2）90AEB CEB ∠=∠=，∴90EBA EAB ∠+∠=， 90ECB EAB ∠+∠=，∴EBA ECB ∠=∠． ∴EBA ECB ∆∆∽， ∴EB EAEC EB=， ∴EB 2=EA ·EC ， ∴AF 2=EA ·EC ．总结：本题考查等腰梯形及相似三角形的判定及性质，注意图形中出现“母子三角形”模型，结合第一问的结论就可以得出待证式. 【难度】3【题目】兴趣篇2ABCD EF如图，ABC ∆是等边三角形，D 是AC 上的一点，BD 的垂直平分线交AB 于E ，交BC 于F.（1） 当点D 在边AC 上移动时，DEF ∆中哪一个角的大小 始终保持不变？并求出它的度数；（2）当点D 在边AC 上移动时，ADE ∆与哪一个三角形始终相似？并写出证明过程．又问：当点D 移动到什么位置时，这两个三角形的相似比为1？（3）若等边三角形ABC 的边长为6，2AD =，试求:BE BF 的值. 【答案】（1）EDF ∠始终不变，且等于60；（2）ADE CFD ∆∆∽，证明见解析；D 移动到AC 中点处时，这两个三角形的相似比为1； （3）45BE BF = 【解析】（1）翻折前后对应角相等，EDF ∠始终不变，且等于60； （2）相似比为1，说明ADE CFD ∆≅∆，得DE DF =； 又DB EF ⊥，所以DB 垂直平分EF ，得BD 平分ABC ∠，则ABC ∆是等边三角形，进而得出结论；（3）45AED CFD C BE DE BF DF C ∆∆=== 总结：本题考查了相似三角形的判定、翻折变换（折叠问题）、相似三角形的性质等的相关知识，通过折叠等边三角形的一个角，可以实现“一线三等角”的效果. 【难度】4【题目】备选试题1ABCDEF如图，在梯形ABCD 中，AB // CD ，90A ∠=︒，2AB =，3BC =，1CD =，点E 是AD的中点.（1） 求证：CDE ∆∽EAB ∆； （2） 证明CDE ∆与CEB ∆相似.【答案】见解析 【解析】（1）证明：过点C 作CF AB ⊥，垂足为F ，如图： 9090A CFB ∠=∠=，，//AD CF ∴，又//AB CD ，∴四边形AFCD 是平行四边形，又90A ∠=，∴平行四边形AFCD 是矩形， 1AF CD AD CF ∴===，，1BF ∴=．在Rt FBC ∆中，2222CF BC BF =-=，22AD ∴=， 点E 是AD 的中点 2ED EA ∴==， ∴22DE CD AB AE ==又90D A ∠=∠=，∴CDE ∆∽EAB ∆．（2）CDE ∆与CEB ∆相似．在Rt DCE ∆中，223CE DC DE =+=， 在Rt CBF ∆中，226BE AE AB =+=，3CE BE CBCD DE CE===， ∴CDE ∆∽CEB ∆． 总结：本题考查了梯形及相似三角形的判定，着重考查学生对相似三角形的判定方法的理解及运用能力．本题实际上是“一线三直角”模型． 【难度】3ABCDEFABCDE【题目】备选试题2如图，已知ABC ∆与ADE ∆都是等边三角形，点D 在BC 边上（点D 不与B 、C 重合），DE 与AC 相交于点F. （1）求证：ABD ∆∽DCF ∆；（2）若BC = 1，设BD = x ，CF = y ，求y 关于x 的函数解析式及定义域； （3）当x 为何值时，79AEF ABD S S ∆∆=？【答案】（1）见解析；（2）y=-x 2+x(0<x<1)；（3）2133x x ==或【解析】（1）ABC ∆、ADE ∆是等边三角形 60,60B C E EDA ∴∠=∠=∠=∠=CDF FDA B DAB ∠+∠=∠+∠,CDF DAB ∴∠=∠ ABD DCF ∴∆∆∽； （2）由（1）得ABD DCF ∆∆∽，AB BDDC CF∴= 11x x y ∴=-()201y x x x ∴=-+<<；（2）易证ABD AEF ∆∆∽， AB ADAE AF∴= 279AEF ABD S AE S AB ∆∆⎛⎫∴== ⎪⎝⎭ 222279AE AF AB AD ∴== ADE ∆是等边三角形 AD AE ∴= 222279AE AF AB AE ∴== 224981AF AB ∴= 1AB = 79AF ∴= 72199y CF ∴==-=， 229x x ∴-+=解得1221,33x x == ∴当2133x x ==或时，79AEF ABD S S ∆∆=． 总结：本题考查旋转的相关知识，本题将相似三角形与旋转部分的知识点结合进行考察，利用“一线三等角”模型能够比较容易找出相似关系.A BCDEF【难度】4。

沪教版上海九年级上册数学相似三角形同步练习一、选择题1、能判定与相似的条件是（）A. B.，且C.且D.，且2、已知两个相似三角形的周长比为4：9，则它们的面积比为（）A．4：9 B．2：3 C．8：18 D．16：493、下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是（）A． B． C． D．4、已知△ABC∽△A′B′C′，下列图形中，△ABC与△A′B′C′不存在位似关系的是( )5、如图，在△ABC中，∠ADE = ∠B，DE ：BC = 2 ：3，则下列结论正确的是（）A. AD : AB = 2 : 3； B．AE : AC = 2:5；C． AD : DB = 2 : 3； D．CE : AE= 3 : 2．6、如图，已知DE∥BC，那么下列结论正确的是（）A． B． C． D．7、如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC相似的是（）A． B． C． D．8、如图，在△ABC中，∠AED=∠B，DE=6，AB=10，AE=8，则BC的长度为（）A．B．C．3 D．9、如图，∠A=∠B=90°，AB=7，AD=2，BC=3，在边AB上取点P，使得△PAD与△PBC相似，则这样的P点共有（）A．1个 B．2个 C．3个 D．4个10、如图所示，在河的一岸边选定一个目标A，再在河的另一岸边选定B和C，使AB⊥BC，然后选定E，使EC⊥BC，用视线确定BC和AE相交于D，此时测得BD=120米，CD=60米，为了估计河的宽度AB，还需要测量的线段是（）A.CEB.DEC.CE或DED.无法确定11、如图，，∠1=∠2，则对于结论：①△ABE∽△ACF；②△ABC∽△AEF；③；④．其中正确的结论的个数是（）A．1 B．2 C．3 D．412、如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（）时，△ABE 与以D、M、N为顶点的三角形相似A． B． C．或 D．或二、填空题13、如图，在△ABC中，D、E分别是AB、AC边上的点（DE不平行于BC），当时，△AED与△ABC相似．14、如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是．（只需写一个条件，不添加辅助线和字母）15、如图，在△ABC 中，D. E 分别是 AB、AC 边的中点，则的值为16、如图，两条直线被第三条直线所截，DE=，EF=，AB=1，则AC= ．17、如图，在△ABC中，∠C=90°，BC=6，D，E分别在AB、AC上，将△ABC沿DE折叠，使点A落在点处，若为CE的中点，则折痕DE的长为．18、在边长为2cm的正方形ABCD中，动点E、F分别从D、C两点同时出发，都以1cm/s的速度在射线DC、CB上移动．连接AE和DF交于点P，点Q为AD的中点．若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似，则运动时间t为秒．三、简答题19、在△ABC中，AB＝12，点E在AC上，点D在AB上，若AE＝6，EC＝4，。