第十章平移旋转轴对称专题复习
- 格式:doc
- 大小:1.72 MB
- 文档页数:6

图形的轴对称平移与旋转本课件是针对《图形的轴对称、平移与旋转》章节的复习内容。
通过本课件的学习,你将能够深入理解图形的轴对称、平移与旋转的概念和特点。
本课件主要包括以下内容:1.轴对称–轴对称的定义–轴对称的特点–轴对称的判定方法–轴对称的性质2.平移–平移的定义–平移的特点–平移的向量表示–平移的性质3.旋转–旋转的定义–旋转的特点–旋转的角度表示–顺时针和逆时针旋转–旋转的性质1. 轴对称1.1 轴对称的定义轴对称是指图形相对于某条轴线能够重合的特性。
如果一个图形经过折叠后能够与原图形完全重合,那么该图形就是轴对称的。
1.2 轴对称的特点轴对称的特点包括: - 对称轴上的每一个点,其关于对称轴的对称点也在图形中; - 图形的每一个点和其对称点的连线和对称轴垂直; - 图形的左右两侧关于对称轴是镜像关系。
1.3 轴对称的判定方法轴对称的判定方法有以下几种: - 观察法:通过观察图形是否满足轴对称的特点; - 折叠法:将图形沿对称轴折叠,观察折叠后的图形是否能够与原图形重合;- 定点法:找出图形上的一些关键点,然后观察这些点与它们关于对称轴的对称点之间是否有对称关系。
1.4 轴对称的性质轴对称具有以下性质: - 轴对称的图形的面积不变; - 轴对称的图形的周长不变; - 轴对称的图形的任意两个对称点之间的距离相等。
2. 平移2.1 平移的定义平移是指图形沿着某个方向不改变形状和大小地移动的过程。
在平移过程中,所有的点都按照相同的方向和距离移动。
2.2 平移的特点平移的特点包括: - 图形平移后形状和大小不变; - 移动前后的图形是全等图形; - 平移不改变图形的朝向。
2.3 平移的向量表示平移可以通过向量进行表示。
如果一个平移将点P(x,y)平移到P’(x’,y’),其中平移向量为v(a,b),那么有以下关系:x’ = x + a,y’ = y + b。
2.4 平移的性质平移具有以下性质: - 平移满足三角不等式,即两个平移的合成平移不超过各自的平移距离之和; - 平移满足平行四边形法则,即平移的结果仍然是平行四边形;- 平移可以逆向进行,即存在逆平移,使得平移后再逆平移回原来的位置。

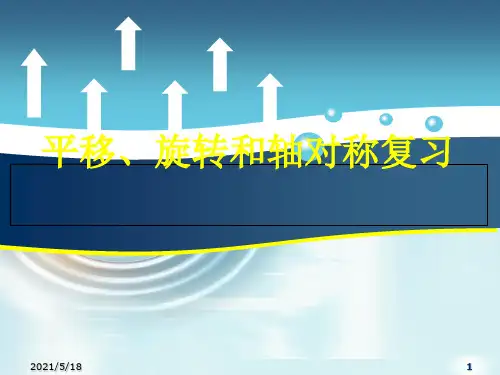
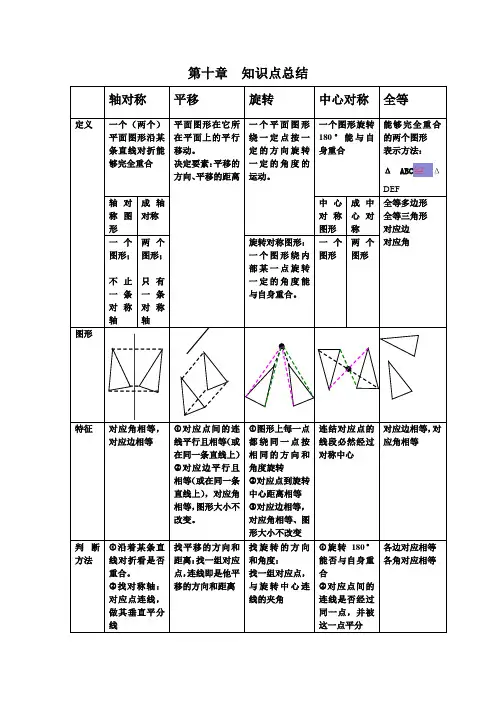


第十章平移、旋转和轴对称知识点一、平移1、平移概念:把一个图形整体沿一方向移动,得到一个新的图形,图形的这种移动,叫做平移变换,简称平移。
2、平移变换的性质①对应线段平行(或共线)且相等;对应点所连结的线段平行且相等,因为经过平移,图形的每个点都沿同一个方向移动了相同的距离,平移变换前后的两条对应线段的四个端点所围成的四边形为平行四边形(四点共线除外)②对应角分别相等,且对应角的两边分别平行,方向一致③平移后的图形与原图形全等,因为平移只改变图形位置,不改变图形的形状和大小3、平移作图步骤①确定平移的方向和距离;②根据对应点的连线平行(或在一条直线上)且相等作出图形各关键点的对应点;③按原图形的连结方式顺次连结各点知识点二、旋转1、旋转概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转。
点O叫做旋转中心,转动的角叫做旋转角。
2、中心对称与中心对称图形中心对称:把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心对称的对称点。
中心对称图形:把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫中心对称图形.3、旋转变换的性质图形通过旋转,图形中每一点都绕着旋转中心沿相同的方向旋转了同样大小的角度,任意一对对应点与旋转中心的连线都是旋转角,对应点到旋转中心的距离相等,对应线段相等,对应角相等,旋转过程中,图形的形状、大小都没有发生变化.4、旋转作图步骤①分析题目要求,找出旋转中心,确定旋转角.②分析所作图形,找出构成图形的关键点.③沿一定的方向,按一定的角度、旋转各顶点和旋转中心所连线段,从而作出图形中各关键点的对应点.④按原图形连结方式顺次连结各对应点.5、中心对称作图步骤①连结决定已知图形的形状、大小的各关键点与对称中心,并且延长2倍,得到各点的对称点.②按原图形的连结方式顺次连结对称点即得所作图形.知识点三、轴对称1、轴对称与轴对称图形轴对称:把一个图形沿着某一条直线折叠,如果能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也叫做这两个图形成轴对称,这条直线叫做对称轴,折叠后重合的对应点,叫做对称点。


第10章轴对称、平移与旋转综合练习一、根底训练选择题:1.以下图案是轴对称图形的有〔〕A、1个 B、2个 C、3个 D、4个第1题图2.以下日常生活现象中,不属于平移的是〔〕A、飞机在跑道上加速滑行B、大楼电梯上上下下地迎送来客C、时钟上的秒针在不断地转动D、滑雪运发动在白茫茫的平坦雪地上滑翔3.下面哪个选项的右边图形与左边图形成轴对称〔〕第3题图4.如右图所示,可以看作是一个菱形通过几次旋转得到的,每次可能旋转〔〕A、30°B、60°C、90°D、150°5.以下说法正确的有〔〕A、1个 B、2个 C、3个 D、4个①用一张相纸冲洗出来的10张1寸相片是全等图形;②我国国旗上的4颗小五角星是全等图形;A B CA ,B ,A BCDEF ③所有的正方形是全等图形;④全等图形的面积一定相等6.假设等腰三角形的周长为26cm ,一边为11cm ,那么腰长为〔 〕A 、11cmB 、7.5cmC 、11cm 或者7.5cmD 、以上都不对—4所示,将矩形纸片先沿虚线AB 按箭头方向向右对折,接着对折后的纸片沿虚线CD 向下对折,然后剪下一个小三角形,再将纸片翻开,那么展开后的图形是〔 〕8.以下由数字组成的式子中,成中心对称的是〔 〕A 、01︰12B 、03︰33C 、08︰80D 、32︰239.以下图形中,①任意四边形:②矩形:③菱形:④正方形:⑤正三角形:⑥等腰直角三角形 ,既是轴对称图形又是中心对称图形的是〔 〕 A 、①②③ B 、②③④ C 、③④⑤ D 、④⑤⑥10.以下说法不正确的选项是〔 〕A 、中心对称图形一定是旋转对称图形B 、轴对称图形一定是中心对称图形C 、在成中心对称的两个图形中,连结对称点的线段都被对称中心平分D 、在平移过程中,对应点所连的线段也可能在一条直线上11.如图5,在正方形ABCD 中,E 为DC 边上的点,连结BE ,将△BCE 绕点C 顺时针旋转900得到△DCF ,连结EF ,假设∠BEC=600,那么∠EFD 的度数为〔 〕A 、100 B 、150 C 、200 D 、250第11题图 第15题图 第16题图CwDBA二、根底延伸填空题:次.“309087〞,那么这串数字是.°,那么此等腰三角形顶角是________.15.如图:把△ABC绕着点C顺时针旋转350,得到△A1B1C,A1B1⊥AC,那么∠A的度数是_________.16.如图:△ABC和△DEF关于点O中心对称,那么△ABC绕点O转了度,AO= .三、才能拓展解答题:17、根据要求,在给出的方格图中画出图形:〔1〕画出四边形ABCD关于点D成中心对称的图形A'B'C'D'.〔2〕将图形A'B'C'D'向右平移8格,再向下平移2格后的图形A"B"C"D".18、如图,在4×3的网格上,由个数一样的白色方块与黑色方块组成一幅图案.请仿照此图案,在以下网格中分别设计出符合要求的图案〔注:①不得与原图案一样;②黑、白方块的个数要一样〕.19、如图:请用一条直线将其分成面积相等的两局部.20、把图中〔实线局部〕补成以虚线L 为对称轴的轴对称图形,你会得到一只美丽的蝴蝶图案.22、如图:点O 在BC 上,△AOC ≌△DOB. 假设∠A=220, ∠B=44O ,求∠AOB 的度数.励志赠言经典语录精选句;挥动**,放飞梦想。

平移旋转轴对称的总结归纳平移、旋转、轴对称是几何学中常见的变换操作,它们在图形的变换中起着重要的作用。
本文将对平移、旋转和轴对称进行总结归纳,以便加深对这些概念的理解。
一、平移平移是指沿着固定的方向和距离,将一个点或者图形在平面内移动。
平移不改变图形的大小、形状和方向,只是改变了图形的位置。
1. 平移的特点- 平移是一种向量运算,其运算结果仍然是一个向量。
- 平移过程中,所有点的位移矢量都相等。
- 平移可以用向量表示,平移向量的起点为原图形上的一个点,终点为其平移后的位置。
2. 平移的表示方法平移可以使用向量运算的方式进行表示,如设平移向量为AB,其中A为原图形上的一个点,B为其平移后的位置。
3. 平移的性质平移具有以下性质:- 平移不改变图形的大小、形状和方向。
- 平移保持图形之间的相对位置关系不变。
二、旋转旋转是指将一个点或者图形按照一定的角度围绕某一点旋转。
旋转可以改变图形的方向,但保持其大小和形状不变。
1. 旋转的特点- 旋转是一种变换运算,将一个点或者图形按照一定的角度绕固定点旋转。
- 旋转可以用角度来描述,旋转角度可以是正数或负数,正数表示逆时针旋转,负数表示顺时针旋转。
- 旋转中心可以是任意点,也可以是图形的某个顶点。
2. 旋转的表示方法旋转可以使用坐标变换的方式进行表示,如设旋转中心为O,旋转角度为θ,则旋转过程中,点P(x, y)绕点O旋转后的新坐标为P'(x', y')。
3. 旋转的性质旋转具有以下性质:- 旋转不改变图形的大小和形状。
- 旋转改变图形的方向。
- 旋转保持图形上的点与中心点之间的距离不变。
三、轴对称轴对称是指图形相对于某条直线对称。
对称轴可以是任意直线,轴对称的图形可以通过对称轴翻转得到自身。
1. 轴对称的特点- 轴对称是一种空间变换,将图形相对于某条直线进行翻转。
- 轴对称的图形具有镜像对称性,即沿对称轴折叠后,两侧图形完全一致。
2. 轴对称的表示方法轴对称可以使用对称关系进行表示,如设对称轴为l,点P关于l的对称点为P',则P'与P关于l对称。

平移、旋转、对称复习与练习知识点1:平移:指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。
平移可以不是水平的。
特征:经过平移,对应线段,对应角分别相等, 对应点所连的线段平行且相等(或共线且相等)。
关键:平移变换不改变图形的形状、大小和方向..,平移前后的两个图形是全等形。
平移二要素:平移的方向、距离。
例题:1.在下列现象中,是平移现象的是()①方向盘的转动②电梯的上下移动③保持一定姿势滑行④钟摆的运动A、①②B、②③C、③④D、①④2.如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是()A、△OCDB、△OABC、△OAFD、△OEF知识点2:旋转:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角。
性质:性质:①对应点到旋转中心的距离相等。
②对应点与旋转中心所连线段的夹角等于旋转角。
③旋转前、后的图形全等。
旋转三要素:旋转的中心、方向、角度。
(注意:三要素中只要任意改变一个......,图形就会不一样。
)例题:1. 将等腰直角△ABC绕直角顶点A按逆时针方向旋转60°后,使点C到点E,点B到点D,得到△ADE,且AB=1。
则EC的长是。
2. 边长为4㎝的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为㎝。
3.如图,已知点O是正三角形ABC三条高的交点,现将△AOB绕点O旋转,使其和△BOC重合,则至少应旋转()A、60°B、120°C、240°D、360°知识点3.轴对称、中心对称、中心对称图形及图案的设计定义:(1)轴对称:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就是轴对称图形。
对称轴:折痕所在的这条直线叫做对称轴。
(2)中心对称:把一个图形绕着某一点旋转180°,如果它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形的对应点叫做关于中心的对称点。
华师大版七年级下册数学第10章轴对称、平移与旋转含答案一、单选题(共15题,共计45分)1、如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,连结ED.若∠B =70°,则∠EDC的大小为()A.10°B.15°C.20°D.30°2、数轴上一点A表示﹣3,若将A点向左平移5个单位长度,再向右平移6个单位长度,则此时A 点表示的数是()A.﹣1B.﹣2C.﹣3.D.13、如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=22°,则∠B的度数是()A.67°B.62°C.82°D.72°4、将一张矩形纸片对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是 ( )A.三角形B.矩形C.菱形D.梯形5、观察下列图案,是轴对称而不是中心对称的是()A. B. C. D.6、请你观察下面四个图形,其中既是轴对称图形又是中心对称图形的是()A. B. C. D.7、如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE 的长为()A. B. C. D.8、如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为().A.(1,2).B.(2,1).C.(2,2).D.(3,1).9、下列不是图形的旋转、平移、轴对称的共同特征的是()A.对应角的大小不变B.图形的大小不变C.图形的形状不变D.对应线段平行10、下列图形中,既是轴对称图形又是中心对称图形的是A. B. C. D.11、下面的每组图形中,左面的图形平移后可以得到右面图形的是()A. B. C. D.12、自新冠肺炎疫情发生以来,全国人民共同抗疫,十堰市张湾区积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A. B. C. D.13、将如图的七巧板的其中几块,拼成一个多边形,为中心对称图形的是( )A. B. C. D.14、下列美丽的图案中,既是轴对称图形又是中心对称图形的个数有()A.1个B.2个C.3个D.4个15、七巧板是一种传统智力游戏,是中国古代劳动人民的发明,用七块板可拼出许多有趣的图形.在下面这些用七巧板拼成的图形中,可以看作轴对称图形的(不考虑拼接线)有()A.5个B.4个C.3个D.2个二、填空题(共10题,共计30分)16、如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长是________.17、如图中,,,中,,,点D在线段AC上,点E在段BC的延长线上,将绕点C旋转得到,则________.18、如图,已知△ABC的面积为16,BC的长为8,现将△ABC沿BC向右平移m 个单位到△A′B′C′的位置。
《轴对称 平移 旋转》复习学案一.[复习前测]1.下列图形中,是中心对称图形的是( ).2.如图1所示的四张牌,若将其中一张牌旋转后得到图2,则旋转的牌是( )3.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形将纸片展开,得到的图形是( )4.如图①~④是四种正多边形的瓷砖图案.其中,是轴对称图形但不是中心对称的图形为( )A .①③B . ①④C .②③D .②④ 5.四张印有汽车品牌标志图案的卡片是中心对称称图形的卡是( )A .B .C .6.如图,△ABC 经过怎样的平移得到△DEF ( ) A .把△ABC 向左平移4个单位,再向下平移2个单位 B .把△ABC 向右平移4个单位,再向下平移2个单位 C .把△ABC 向右平移4个单位,再向上平移2个单位 D .把△ABC 向左平移4个单位,再向上平移2个单位7.如图,已知梯形中,,,相交于点,,则下列说法错误的是( ) A .梯形是轴对称图形 B .C .梯形是中心对称图形D .平分8.下面的图形中,既是轴对称图形又是中心对称图形的是( )9.如图所示,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 中点E 处,点A 落在F 处,折痕为MN ,则线段CN 的长是( )A. 2B. 3C. 4D. 5二、[体系再现]图形的平移、旋转、轴对称知识结构图:1.图形平移两要素:平移方向,平移距离;平移的特点:平移不改变图形的形状和大小.图形平移的作图中要注意以下几点:①首先确定图形中的关键点;②将这些关键点沿指定的方向移动指定的单位距离;③然后连接对应的部分形成相应的图形.2.图形旋转要素:旋转中心,旋转方向,旋转角度;图形旋转的特点:旋转不改变图形的形状和大小.图形旋转的作图中要注意以下几个问题:①首先确定旋转中心;②其次确定图形的关键点;③将这些关键点沿指定的方向旋转指定的角度;④然后连接对应的部分,形成相应的图形.3.中心对称在平面内,将一个图形绕着中心旋转180°后能与自身重合,则这种图形叫做中心对称图形,这个中心叫做对称中心.中心对称图形的特点:图形绕着它自身的中心旋转180°后能与自身重合.在图形中心对称的作图中要注意以下几点:①首先确定图形的对称中心;②其次确定图形的关键点;③作这些关键点关于对称中心的对称点;④最后连接对应的部分,形成相应的图形.三、[重点讲解]1、典例剖析考点之一:考查轴对称图形的识别给出一些图案、图形或图形的名称,要求判断是不是轴对称图形.例1:下列交通标志图中,属于轴对称图形的是()考点之二:考查文字中的轴对称主要考查文字、数字及字母的轴对称问题.例2:小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是___,考点之三:考查镜子里的轴对称主要考查实际物体与镜子里的像之间的关系.例3(安徽省课改区)小亮在镜中看到身后墙上的时钟如下,你认为实际时间最接近八点的是()考点之四:考查折纸中的轴对称主要考查折纸时对折痕两边的图形或部分图形关于折痕为对称轴的认识.例4:如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数α满足().A.︒<<︒18090α;B.︒=90α;HGFEDC BAC.︒<<︒900α;D.α随着折痕位置变化而变化. 考点之五:考查剪纸中的轴对称主要考查一定形状的纸按一定的规律折叠后裁剪掉一部分,然后识别展开后的形状.例5:如图所示,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上;叠完后,剪一个直径在BC上的半圆,再展开,则展开后的图形为( )考点之六:考查轴对称作图主要考查按某种要求作一个图形的轴对称图形.例6:如图,一个轴对称图形画出了它的一半,请你以点画线为对称轴画出它的另一半.考点之七:考查轴对称方案设计主要考查根据提供的材料按要求设计一个轴对称图形.例7:国卫公司办公大楼前有一个15m×30m的矩形广场,广场中央已建成一个半径为4m的圆形花圃(其圆心与矩形对角线的交点重合).现欲建一个半径为2米与花圃相外切的圆形喷水池,使得建成后的广场、花铺和喷水池构成的平面图形是一个轴对称图形.则符合条件的喷水池的位置有___个.2.能力提升1.下列图形中是轴对称图形的是 ( )2.如图,把一张长方形纸片对折,折痕为AB ,再以AB 的中点O 为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O 为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )A .正三角形 B.正方形 C .正五边形 D .正六边形 3.下列图形中,既是轴对称图形又是中心对称图形的是( )A. 菱形B.梯形C.正三角形 D.正五边形4.右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是( )A.①⑤ B .②④ C .③⑤ D .②⑤5.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )A .六边形B .八边形C .十二边形D .十六边形 6.下列图形中既是轴对称图形,又是中心对称图形的是( )B C BC G B D C AC B A7.如图2,将矩形纸片ABCD (图1)按如下步骤操作:(1)以过点A 的直线为折痕折叠纸片,使点B 恰好落在AD 边上,折痕与BC 边交于点E (如图2);(2)以过点E 的直线为折痕折叠纸片,使点A 落在BC 边上,折痕EF 交AD 边于点F (如图3);(3)将纸片收展平,那么∠AFE 的度数为( B ).(A )60° (B )67.5° (C )72° (D )75°四、真题选做1.如图,D 是AB 边上的中点,将△ABC 沿过D 的直线折叠,使点A 落在BC 上F 处,若∠B=50°,则∠BDF=__ __2.下列图形中,中心对称图形有( ).A.1个 B .2个 C .3个 D .4个 3.以下图形中,既是轴对称图形,又是中心对称图形的是A .等边三角形B .矩形C .等腰梯形D .平行四边形 4.图中的小方格都是边长为1的正方形,△ABC 的顶点和O 点都在正方形的顶点上. (1)以点O 为对称中心,在方格图中作出△ABC 的中心对称图形△A ′B ′C ′;(2)△A ′B ′C ′绕点B ′顺时针旋转90,画出旋转后得到的△A ″B ′C ″,并求边A ′B ′在旋转过程中扫过的图形面积.5.如图,ΔABC 与ΔA ’B ’C ’关于直线l 对称,则∠B 的度数为 ( ) A .50° B .30° C .100° D .90°6.下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是( )A 、B 、C 、D 、7.在小正方形组成的15×15的网络中,四边形ABCD 和四边形A ′B ′C ′D ′的位置如图所示。
⑴现把四边形ABCD 绕D 点按顺时针方向旋转900,画出相应的图形1111D C B A ,⑵若四边形ABCD 平移后,与四边形A ′B ′C ′D ′成轴对称,写出满足要求的一种平移方法,并画出平移后的图形2222D C B A30︒lC'B'A'B C A 50︒8.已知以下四个汽车标志图案:其中是轴对称图形的图案是 (只需填入图案代号).9.下面的图形中,既是轴对称图形又是中心对称图形的是()(A)(B) (C) (D) 五、目标检测 (一)、选择题 1.(20XX 年广州中考数学模拟试题一)如图所示的图案中是轴对称图形的是( )2.下列四个图形中,既是轴对称图形,又是中心对称图形的是( )A 、①②B 、①③C 、②③D 、①②③ 3.下图是用纸叠成的生活图案,其中不是轴对称图形的是( )A .信封B .飞机C .衬衣D .衬衣4、已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1(如图4所示) 把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为__或___.5.如图,F 是梯形ABCD 的下底BC 上的一点,若将△DFC 沿DF 进行折叠,点C 恰好能与AD 上的E 重合,那么四边形CDEF A.是轴对称图形但不是中心对称图形 B.是中心对称图形但不是轴对称图形 C.既是轴对称图形,也是中心对称图形 D.既不是轴对称图形,也不是中心对称图形 6.(2010浙江永嘉)下列图形中,既是轴对称图形又是中心对称图形的有( )第6题A .4个B .3个C .2个D .1个7.京剧是我国的国粹,剪纸是流传已久的民间艺术,这两者的结合无疑是最能代表中国特色的艺术形式之一.图中京剧脸谱剪纸中是轴对称图形的个数是( ) A .1个 B .2个 C .3个 D .4个8.用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是( )A .平移和旋转B .对称和旋转C .对称和平移D .旋转和平移12.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )(二)、填空题1.如图,镜子中号码的实际号码是_________ .2.等边三角形、平行四边形、矩形、圆四个图形中,既是轴对称图形又是中心对称图形的是 . (三)、解答题1. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐 标系后,△ABC 的顶点均在格点上,点C 的坐标为 (0, -1),(1) 写出A 、B 两点的坐标;(2) 画出△ABC 关于y 轴对称的△A 1B 1C 1 ;(3) 画出△ABC 绕点C 旋转180°后得到的△A 2B 2C 2 。
(第9题图)垂直A .B .C .D .。