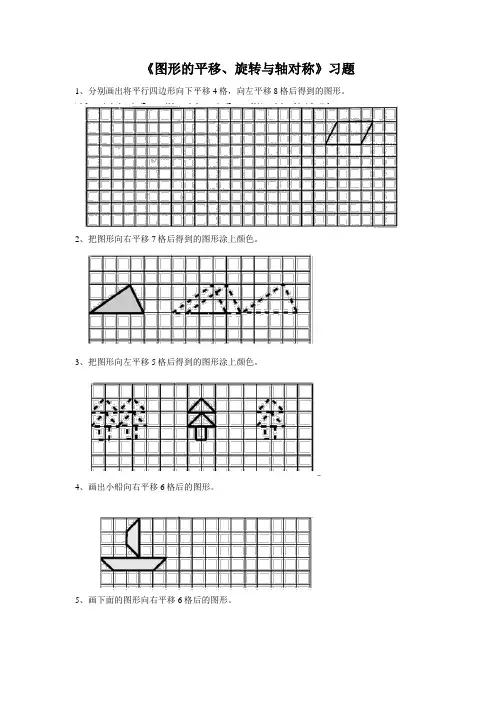
平移旋转与轴对称练习
- 格式:docx
- 大小:111.44 KB
- 文档页数:4

图形的对称、平移和旋转专项训练题一.选择题(共9小题)1.以下是几所知名大学的校徽,其中是轴对称图形的是()A.B.C.D.2.下列图形中,既是轴对称图形也是中心对称图形的有()A.4个B.3个C.2个D.1个3.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕AD.将△ABC再次折叠,使BC边落在BA边上,展开后得到折痕BE,BE,AD交于点O.则以下结论一定成立的是()A.AO=2OD B.S△ABO=S四边形ODCEC.点O到△ABC三边的距离相等D.点O到△ABC三个顶点的距离相等4.下列各式中,是中心对称图形的是()A.B.C.D.5.下列图形中,既是中心对称图形也是轴对称图形的是()A.B.C.D.6.把点P(2,﹣5)向上平移3个单位后再关于原点对称的点的坐标是()A.(5,﹣5)B.(﹣2,2)C.(﹣5,5)D.(2,﹣2)7.如图,△ABC的周长为30cm,将△ABC沿CB向右平移得到△DEF,若平移的距离为4cm,则四边形ACED的周长是()cm.A.34B.36C.38D.408.“会飞的饺子皮”刷爆朋友圈,卡塔尔世界杯吉祥物“拉伊卜”刷爆网络!下面是“拉伊卜”的形象图片,在下面的四个图形中,能由左图经过平移得到的图形是()A.B.C.D.9.通过光的反射定律知道,入射光线与反射光线关于法线成轴对称(图1).在图2中,光线自点P射入,经镜面EF反射后经过的点是()A.点A B.点B C.点C D.点D二.填空题(共8小题)10.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC,第1次折叠使点B落在BC边上的点B'处,折痕AD交BC于点D;第2次折叠使点A落在点D处,折痕MN交AB'于点P.若BC=12,则MP+MN=.11.如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则sin∠ADF的值为.12.如图,将△ABC绕点C顺时针旋转30°得到△DEC,边ED,AC相交于点F,若∠A=32°,则∠EFC的度数为°.13.如图,在△ABC中,BC=7,把△ABC沿射线AB方向平移4个单位至△EFG处,EG与BC交于点M.若CM=3,则图中阴影部分的面积为.14.在平面直角坐标系中,将点(1,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得的点的坐标是.15.如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE交CD于点H,且DH=EH,则AH的长为.16.等腰直角△ABC中,BAC=90°,AB=5,点D是平面内一点,AD=2,连接BD,将BD绕D点逆时针旋转90°得到DE,连接AE,当DAB=(填度数)度时,AE 可以取最大值,最大值等于.17.如图,矩形ABCD的边AD的长为6,将△ADC沿对角线AC翻折得到△AD′C,CD′与AB交于点E,再以CD′为折痕,将△BCE进行翻折,得到△B′CE,若两次折叠后,点B′恰好落在△ADC的边上,则AB的长为.三.解答题(共3小题)18.如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均在格点(网格线的交点)上.(1)将△ABC向右平移5个单位长度,再向下平移2个单位长度,画出△ABC平移后的图形△A1B1C1;(2)以点A为旋转中心,将△ABC按逆时针方向旋转90°,得到△AB2C2,请画出△AB2C2.19.已知O是坐标原点,的坐标分别为(3,1),(2,﹣1).(1)画出绕点O顺时针旋转90°后得到的,并写出A1的坐标为;(2)在y轴的左侧以O为位似中心作的位似图形,使新图与原图相似比为2:1;(3)若点D(a,b)在线段OA上,直接写出变化(2)后点D的对应点D2的坐标为.20.如图,在正方形网格中,△ABC各顶点都在格点上,点A,B,C的坐标分别为(﹣5,1),(﹣5,4),(﹣1,4).(1)画出△ABC关于y轴对称的△A1B1C1,点A,B,C的对应点分别是A1、B1、C1.(2)画出△ABC关于原点O对称的△A2B2C2,点A,B,C的对应点分别是A2、B2、C2.。

三年级上册数学单元测试- 6.平移、旋转和轴对称一、单选题1.下列现象中,既有平移现象又有旋转现象的是()A. 正在工作的电扇叶片B. 行驶中的汽车C. 扔出去的铅球D. 放飞的风筝2.如图。
将图1中的三角形甲平移到图2中所示的位置,与三角形乙拼成一个长方形,那么,下面的平移方法中,正确的是( )。
A. 先向下平移3格,再向右平移1格B. 先向下平移3格.再向右平移2格C. 先向下平移2格,再向F平移2格D. 先向有平移3格.再向F平移2格3.电风扇的运动是()A. 平移B. 旋转C. 既平移又旋转4.图①绕点O()变为图②。
A. 顺时针旋转90°B. 逆时针旋转180°C. 逆时针旋转90°5.一个图形经过平移变换后,有以下几种说法,其中不恰当的说法是( )A. 平移后,图形的形状和大小都不改变B. 平移后的图形与原图形的对应线段、对应角都相等C. 平移后的图形形状不变,但大小可以改变D. 利用基本图形的平移可以设计美丽的图案6.从12时到12时30分,分针绕中心点()。
A. 逆时针旋转了90°B. 顺时针旋转了90°C. 顺时针旋转了180°7.下列哪种运动可以看成平移()A. 升国旗B. 电风扇叶片转动C. 钟摆的运动8.下列每组中的前后两个图形,()组通过平移就可以重合。
A. B. C. D.9.补全轴对称图形的时候,要先找到()A. 边界B. 对称轴C. 端点10.下列现象中,不属于平移的是()A. 乘直升电梯从一楼上到二楼B. 钟表的指针嘀嗒嘀嗒地走C. 火车在笔直的轨道上行驶D. 汽车在平坦笔直的公路上行驶二、判断题11.平移必须在水平方向上移动。
12.收费站转杆打开,旋转了180度。
13.电风扇转动是平移现象。
14.左图是由连续两次向右平移2个方格组成的图案。
15.小朋友们玩跷跷板是平移现象。
三、填空题16.看图回答图形B可以看作图形A绕点________顺时针方向旋转90°得到的。
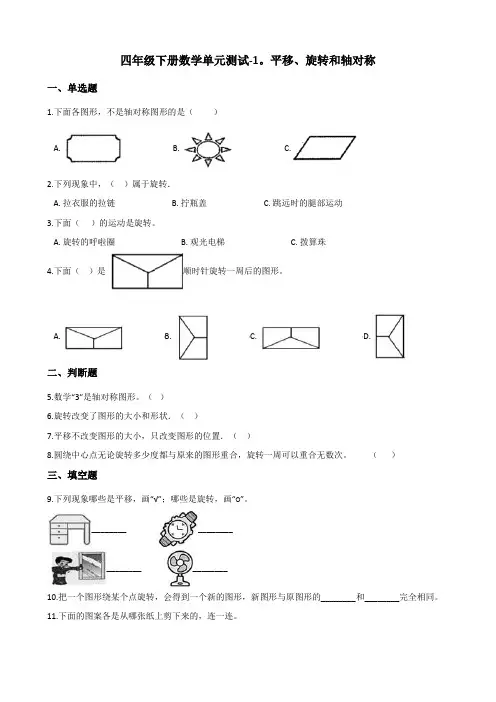
四年级下册数学单元测试-1。
平移、旋转和轴对称一、单选题1.下面各图形,不是轴对称图形的是()A. B. C.2.下列现象中,()属于旋转.A. 拉衣服的拉链B. 拧瓶盖C. 跳远时的腿部运动3.下面()的运动是旋转。
A. 旋转的呼啦圈B. 观光电梯C. 拨算珠4.下面()是顺时针旋转一周后的图形。
A. B. C. D.二、判断题5.数学“3”是轴对称图形。
()6.旋转改变了图形的大小和形状.()7.平移不改变图形的大小,只改变图形的位置.()8.圆绕中心点无论旋转多少度都与原来的图形重合,旋转一周可以重合无数次。
()三、填空题9.下列现象哪些是平移,画“√”;哪些是旋转,画“○”。
________ ________________ ________10.把一个图形绕某个点旋转,会得到一个新的图形,新图形与原图形的________和________完全相同。
11.下面的图案各是从哪张纸上剪下来的,连一连。
________ A、________ B、________ C、________ D、四、解答题12.解决问题如图,正方体中哪些线段可经由线段AB平移得到?线段AD可以由FB平移得到吗?13.(1)沿虚线画出图形的另一半,使它成为一个轴对称图形。
(2)图中的小船是经过向________平移________格,再向________平移________格得来的。
(3)先将三角形向左平移三格,然后绕A点逆时针旋转90°,在方格纸中画出旋转后的图形。
五、应用题14.在下面的方格纸上:①用数对表示三角形A三个顶点的位置.(,)(,)(,)②画出图形A向右平移8格后得到图形B;然后再以MN为对称轴,画出B的轴对称图形.参考答案一、单选题1.【答案】C【解析】【解答】平行四边形不是轴对称图形。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴。

初中数学图形的平移,对称与旋转的经典测试题附答案一、选择题1.如图,在R t △ABC 中,∠ACB=90°,∠B=60°,BC=2,∠A ′B ′C ′可以由△ABC 绕点C 顺时针旋转得到,其中点A′与点A 是对应点,点B′与点B 是对应点,连接AB′,且A 、B′、A′在同一条直线上,则AA′的长为( )A .43B .6C .33D .3【答案】B【解析】【分析】【详解】 试题分析:∵在Rt △ABC 中,∠ACB=90°,∠B=60°,BC=2,∴∠CAB=30°,故AB=4,∵△A ′B ′C 可以由△ABC 绕点C 顺时针旋转得到,其中点A′与点A 是对应点,点B′与点B 是对应点,连接AB′,且A 、B′、A′在同一条直线上,∴AB=A ′B ′=4,AC=A′C ,∴∠CAA ′=∠A ′=30°,∴∠ACB ′=∠B ′AC=30°,∴AB ′=B ′C=2,∴AA ′=2+4=6.故选B .考点:1、旋转的性质;2、直角三角形的性质2.如图,DEF ∆是由ABC ∆经过平移后得到的,则平移的距离不是( )A .线段BE 的长度B .线段EC 的长度、两点之向的距离C.线段CF的长度D.A D【答案】B【解析】【分析】平移的距离是平移前后对应两点之间连线的距离,根据这可定义可判定【详解】∵△DEF是△ABC平移得到∴A和D、B和E、C和F分别是对应点∴平移距离为:线段AD、BE、CF的长故选:B【点睛】本题考查平移的性质,在平移过程中,我们通常还需要注意,平移前后的图形是全等图形.a a>,那么3.在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数(1)所得的图案与原来图案相比()A.形状不变,大小扩大到原来的a倍B.图案向右平移了a个单位C.图案向上平移了a个单位D.图案向右平移了a个单位,并且向上平移了a个单位【答案】D【解析】【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.【详解】在直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加上正数a(a>1),那么所得的图案与原图案相比,图案向右平移了a个单位长度,并且向上平移了a个单位长度.故选D.【点睛】本题考查了坐标系中点、图形的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.4.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是()A.主视图B.左视图C.俯视图D.主视图和左视图【答案】C【解析】【分析】根据所得到的主视图、俯视图、左视图结合中心对称图形的定义进行判断即可.【详解】观察几何体,可得三视图如图所示:可知俯视图是中心对称图形,故选C.【点睛】本题考查了三视图、中心对称图形,正确得到三视图是解决问题的关键.5.已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为()A.(5,3)B.(﹣1,﹣2)C.(﹣1,﹣1)D.(0,﹣1)【答案】C【解析】【分析】根据点A、点A的对应点的坐标确定出平移规律,然后根据规律求解点B的对应点的坐标即可.【详解】∵A(1,3)的对应点的坐标为(﹣2,1),∴平移规律为横坐标减3,纵坐标减2,∵点B(2,1)的对应点的坐标为(﹣1,﹣1),故选C.【点睛】本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,本题根据对应点的坐标确定出平移规律是解题的关键.6.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,3),且|a﹣7b ,将线段PQ向右平移a个单位长度,其扫过的面积为20,那么a+b+c的值为()A.12 B.15 C.17 D.20【答案】C【解析】【分析】由非负数的性质得到a=c,b=7,P(a,7),故有PQ∥y轴,PQ=7-3=4,由于其扫过的图形是矩形可求得a,代入即可求得结论.【详解】b =0,∵且|a-c|++7∴a=c,b=7,∴P(a,7),PQ∥y轴,∴PQ=7-3=4,∴将线段PQ向右平移a个单位长度,其扫过的图形是边长为a和4的矩形,∴4a=20,∴a=5,∴c=5,∴a+b+c=5+7+5=17,故选C.【点睛】本题主要考查了非负数的性质,坐标的平移,矩形的性质,能根据点的坐标判断出PQ∥y 轴,进而求得PQ是解题的关键.7.在下面由冬季奥运会比赛项目图标组成的四个图形中,其中可以看作轴对称图形的是()A.B.C.D.【答案】D【解析】【分析】根据轴对称图形的概念对各选项分析判断即可得解.【详解】A、不是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、是轴对称图形,故本选项正确.故选:D.【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.8.如图,在ABC V 中,60,3,5,B AB BC ∠=︒==将ABC V 绕点A 顺时针方向旋转得到,ADE V 当点B 的对应点D 恰好落在BC 边上时,则CD 的长为( )A .3B .2.5C .2D .1【答案】C【解析】【分析】 由旋转得到AD=AB ,由此证明△ADB 是等边三角形,得到BD=AB=3,即可求出CD.【详解】由旋转得AD=AB ,∵60B ∠=︒,∴△ADB 是等边三角形,∴BD=AB=3,∴CD=BC-BD=5-3=2,故选:C.【点睛】此题考查旋转的性质,等边三角形的判定及性质,根据旋转得到AD=AB 是解题的关键,由此得到等边三角形进行求解.9.下列四个交通标志图中,是轴对称图形的是( )A .B .C .D .【答案】B【解析】【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.【详解】A 、不是轴对称图形,故本选项错误;B 、是轴对称图形,故本选项正确;C 、不是轴对称图形,故本选项错误;D 、不是轴对称图形,故本选项错误.故选B .【点睛】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.10.如图,若将线段AB平移至A1B1,则a+b的值为( )A.﹣3 B.3 C.﹣2 D.0【答案】A【解析】【分析】根据点的平移规律即点A平移到A1得到平移的规律,再按此规律平移B点得到B1,从而得到B1点的坐标,于是可求出a、b的值,然后计算a+b即可.【详解】解:∵点A(0,1)向下平移2个单位,得到点A1(a,﹣1),点B(2,0)向左平移1个单位,得到点B1(1,b),∴线段AB向下平移2个单位,向左平移1个单位得到线段A1B1,∴A1(﹣1,﹣1),B1(1,﹣2),∴a=﹣1,b=﹣2,∴a+b=﹣1﹣2=﹣3.故选:A.【点睛】本题考查了直角坐标系中点的平移规律,解决本题的关键是熟知坐标平移规律上加下减、右加左减.11.对于图形的全等,下列叙述不正确的是()A.一个图形经过旋转后得到的图形,与原来的图形全等B.一个图形经过中心对称后得到的图形,与原来的图形全等C.一个图形放大后得到的图形,与原来的图形全等D.一个图形经过轴对称后得到的图形,与原来的图形全等【答案】C【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,故选C.【点睛】本题考查了对全等图形的认识,解题的关键是要明确通过旋转、轴对称、平移等都可以得到与原图形全等的图形,而通过放大或缩小只能得到与原图形形状一样的图形,得不到全等图形.12.如图,ABC V 的三个顶点都在方格纸的格点上,其中点A 的坐标是()1,0-.现将ABC V 绕点A 顺时针旋转90︒,则旋转后点C 的坐标是( )A .()3,3B .()2,1C .()4,1--D .()2,3【答案】B【解析】【分析】 在网格中绘制出CA 旋转后的图形,得到点C 旋转后对应点.【详解】如下图,绘制出CA 绕点A 顺时针旋转90°的图形由图可得:点C 对应点的坐标为(2,1)故选:B【点睛】本题考查旋转,需要注意题干中要求顺时针旋转还是逆时针旋转.13.如图,一个长为2、宽为1的长方形以下面的“姿态”从直线l 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( )A .1B .2C .3D .22【答案】C【解析】【分析】根据平移的性质即可解答.【详解】如图连接AA ',根据平行线的性质得到∠1=∠2,如图,平移的距离AA '=的长度123=+=故选C.【点睛】此题考查平移的性质,解题关键在于利用平移的性质求解.14.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .【答案】C【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【详解】A 、是轴对称图形,不是中心对称的图形,故本选项不符合题意;B 、不是轴对称图形,是中心对称的图形,故本选项不符合题意;C 、既是轴对称图形,又是中心对称的图形,故本选项符合题意;D 、是轴对称图形,不是中心对称的图形,故本选项不符合题意.故选:C .【点睛】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.15.如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上,点()5,3D 在边AB 上,以C 为中心,把CDB △旋转90︒,则旋转后点D 的对应点'D 的坐标是( )A .()2,10B .()2,0-C .()2,10或()2,0-D .()10, 2或()2,0-【答案】C【解析】【分析】 先根据正方形的性质求出BD 、BC 的长,再分逆时针旋转和顺时针旋转两种情况,然后分别根据旋转的性质求解即可得.【详解】Q 四边形OABC 是正方形,(5,3)D5,3,2,90BC OC AB OA AD BD AB AD B ∴======-=∠=︒由题意,分以下两种情况:(1)如图,把CDB △逆时针旋转90︒,此时旋转后点B 的对应点B '落在y 轴上,旋转后点D 的对应点D ¢落在第一象限由旋转的性质得:2,5,90B D BD B C BC CB D B '''''====∠=∠=︒10OB OC B C ''∴=+=∴点D ¢的坐标为(2,10)(2)如图,把CDB △顺时针旋转90︒,此时旋转后点B 的对应点B ''与原点O 重合,旋转后点D 的对应点D ''落在x 轴负半轴上由旋转的性质得:2,5,90B D BD B C BC CB D B ''''''''''====∠=∠=︒∴点D ''的坐标为(2,0)-综上,旋转后点D 的对应点D ¢的坐标为(2,10)或(2,0)-故选:C .【点睛】本题考查了正方形的性质、旋转的性质等知识点,依据题意,正确分两种情况讨论是解题关键.16.如图,将△ABC 绕点C (0,1)旋转180°得到△A'B'C ,设点A 的坐标为(,)a b ,则点的坐标为( )A .(,)a b --B .(,1)a b ---C .(,1)a b --+D .(,2)a b --+【答案】D【解析】 试题分析:根据题意,点A 、A′关于点C 对称,设点A 的坐标是(x ,y ),则 0122a xb y ++==,,解得2x a y b =-=-+,,∴点A 的坐标是(2)a b --+,.故选D . 考点:坐标与图形变化-旋转.17.如图,点E 是正方形ABCD 的边DC 上一点,把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置.若四边形AECF 的面积为20,DE=2,则AE 的长为( )A .4B .5C .6D .26【答案】D【解析】【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积,进而可求出正方形的边长,再利用勾股定理得出答案.【详解】Q绕点A顺时针旋转90︒到ABFADE∆∆的位置.∴四边形AECF的面积等于正方形ABCD的面积等于20,∴==,AD DC25Q,2DE=∴∆中,2226Rt ADE=+=AE AD DE故选:D.【点睛】本题主要考查了旋转的性质以及正方形的性质,正确利用旋转的性质得出对应边关系是解题关键.18.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4 B.5 C.6 D.7【答案】B【解析】试题解析:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.此时DP+CP=DP+PC′=DC′的值最小.∵DC=1,BC=4,∴BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC22'+22BC BD+.故选B.3419.下列图形中,不一定是轴对称图形的是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形【答案】C【解析】A.等腰三角形是轴对称图形,不符合题意;B.等边三角形是轴对称图形,不符合题意;C.直角三角形不一定是轴对称图形,符合题意;D.等腰直角三角形是轴对称图形,不符合题意.故选C.20.中国文字博大精深,而且有许多是轴对称图形,在这四个文字中,不是轴对称图形的是()A.B.C.D.【答案】D【解析】【分析】如果一个图形沿着一条直线对折后两部分完全重合,那么这样的图形就叫做轴对称图形.【详解】A.是轴对称图形;B.是轴对称图形;C.是轴对称图形;D.不是轴对称图形;故选D.【点睛】本题考查的是轴对称图形,熟练掌握轴对称图形的概念是解题的关键.。

西师版五年级数学上册图形的平移、旋转与轴对称练习题2.1 图形的平移1.一个边长为6厘米的正方形,连续向右平移6次后,这个正方形的边长是多少厘米?2.方格中的图形向左平移了几个格?3.图形先由位置①向上平移几个格,到位置②;再由位置②向右平移几个格,到位置③。
4.图形平移的过程中对应点间的距离都保持不变,图形平移后周长和面积不变。
5.下列图形中,由原图平移得到的图形是哪一个?2.2 图形的旋转1.一个边长为6厘米的等腰三角形,连续顺时针旋转4次后,和原图形重合。
2.分针从6:30到6:45,旋转了多少度?3.把图形绕着O点顺时针旋转90°后,得到的图形是哪一个?A。
B。
C。
D.4.旋转不能改变图形的形状,可以改变图形的位置。
5.时钟从3:00到6:00,时针顺时针旋转了多少度?2.3 轴对称图形1.直角梯形是轴对称图形。
2.下面交通标志图案中,是轴对称图形的是哪一个?A。
B。
C.3.下面的图形中,哪一个不是轴对称图形?A。
B。
C.4.正方形对称轴有无数条。
5.下面图形中,哪一个对称轴最多?A。
正方形 B。
等边三角形 C。
圆 D。
长方形2.4 设计图案1.图形的平移、旋转和对称都是图形的变换方式。
2.如图的图形中,哪一个是由旋转得到的?A。
B。
C。
D.3.平移和旋转不能改变图形的形状,可以改变图形的位置。
4.下面的图案是通过哪种变换得到的?5.下图的图案,既可以通过平移得到,又可以通过旋转得到。
A。
B。
C.2.5 探索规律1.看图填空。
摆1个平行四边形需要几根小棒。
摆2个平行四边形需要几根小棒。
摆3个平行四边形需要几根小棒。
2.观察下图第4个图形中有几个三角形。
3.摆1个三角形需要3根小棒;摆2个三角形至少需要几根小棒?4.第五个图形有多少个圆点?5.数一数梯形的个数。
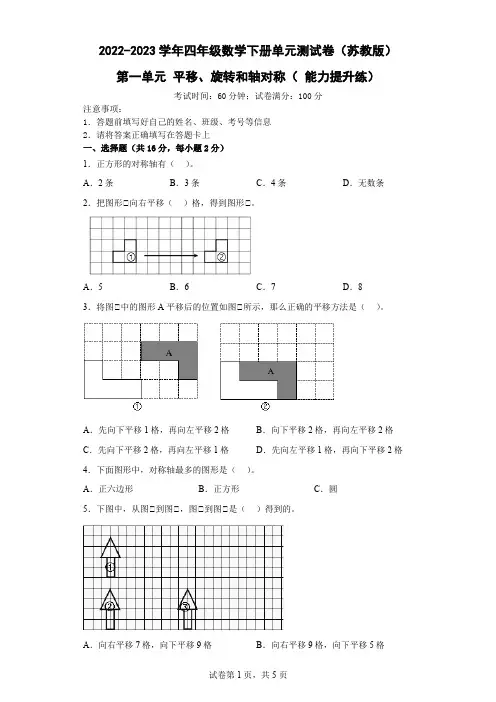
二、下面的实线图形是通过怎样的平移得到的虚线图形的。
平行四边形向右平移5格;三角形向下平移2格;长方形向上平移3格;六边形向左平移4格。

三年级数学平移旋转和对称试题1.电梯的升降是现象,钟面上时针和分针的运动是现象,拉开抽屉时,抽屉做运动.【答案】平移,旋转,平移.【解析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,所以,它并不一定是绕某个轴的,根据平移与旋转定义判断即可.解答:解:电梯的升降是平移现象,钟面上时针和分针的运动是旋转现象,拉开抽屉时,抽屉做平移运动;故答案为:平移,旋转,平移.点评:本题是考查图形的平移与旋转的意义,关键是看方向是否改变.2.推拉窗户的运动是;风车的运动是.【答案】平移,旋转.【解析】(1)平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;(2)旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,所以,它并不一定是绕某个轴的;依此根据平移与旋转定义判断即可.解:推拉窗户的运动是平移;风车的运动是旋转;故答案为:平移,旋转.【点评】此题是对平移与旋转理解及在实际当中的运用.3.下列图形中,不是轴对称图形的是()A.B.C.D.【答案】D【解析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.解:根据轴对称图形的意义可知:下列图形中,不是轴对称图形的是,其它三个选项中的图形都是轴对称图形;故选:D.【点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.4.周一升国旗时,国旗的上升是现象;拧水龙头是现象.【答案】平移,旋转.【解析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的;然后根据平移与旋转定义判断即可.解:周一升国旗时,国旗的上升是平移现象;拧水龙头是旋转现象;故答案为:平移,旋转.【点评】本题是考查图形的平移与旋转.平移与旋转关键是看图形的方向是否改变,平移不改变方向,旋转改变方向.5.在横线里填上“平移”或“旋转”.(1)自行车车轮的转动是现象,人骑车前行是现象;(2)风扇叶片的运动是现象;(3)钟面上分针不停地走动是现象;(4)升国旗时,国旗的升降运动是现象;(5)拉开抽屉是现象,拧水龙头是现象.【答案】旋转,平移;旋转;旋转;平移;平移,旋转.【解析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的;由此根据平移与旋转定义判断即可.解:(1)自行车车轮的转动是旋转现象,人骑车前行是平移现象;(2)风扇叶片的运动是旋转现象;(3)钟面上分针不停地走动是旋转现象;(4)升国旗时,国旗的升降运动是平移现象;(5)拉开抽屉是平移现象,拧水龙头是旋转现象.故答案为:旋转,平移;旋转;旋转;平移;平移,旋转.【点评】此题是对平移与旋转理解及在实际当中的运用.6.下列现象属于平移现象的是()A.风扇转动B.写字C.晃动呼啦圈D.转动风车【答案】B【解析】根据平移不改变图形的形状、大小和方向,结合图形对选项进行一一分析,选出正确答案.解:A.图形的方向发生变化,不符合平移的性质,不属于平移得到,故本选项错误;B.图形的形状和大小没有变化,符合平移的性质,属于平移得到,故本选项正确;C.图形的方向发生变化,不符合平移的性质,不属于平移得到,故本选项错误;D.图形的方向发生变化,不符合平移的性质,不属于平移得到,故本选项错误.故选:B.【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.7.“里,一,五”都是轴对称的汉字.(判断对错)【答案】错误【解析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.解:根据轴对称图形的意义可知:“里,一”都是轴对称的汉字,而“五”不是轴对称图形;故答案为:错误.【点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.8.动手画一画、比一比在方格中画出一个轴对称图形。

苏教版三年级上册数学第六单元平移、旋转和轴对称同步练习一.选择题1.小聪推门进了教室,推门时门在()。
A.平移B.旋转C.对称2.铅笔平移后的线条是()的。
A.互相平行B.不平行C.互相垂直3.把一张长方形纸对折后再对折,沿着折痕所在的直线画出心形的一半,把它沿边缘线剪下来,能剪出( )个完整的心形。
A.1B.2C.44.下面的第一个图形是通过()变成第二个图形的。
A.旋转B.平移C.对称5.开动的火车,车厢的运动是(),车轮的运动是()。
A.平移B.旋转C.左移二.判断题1.张叔叔在公路上开车,方向盘的运动是平移现象。
()2.转动的转盘属于旋转现象。
()3.英文字母中的“Z”、“S”都是轴对称图形。
()4.电动门的开关不是平移现象。
()5.圆不是轴对称图形。
()三.填空题1.打开水龙头时,水龙头的运动是()现象;国旗的升降运动是()现象。
(填“平移”或“旋转”)。
2.红领巾的平面图形有()条对称轴。
3.物体沿直线上、下、左、右运动,这样的现象叫做________;物体绕一个固定点弧线运动,这样的现象叫做________。
4.长方形有()条对称轴。
5.下列现象是平移的画“□”,是旋转的画“△”。
()()()()四.作图题1.先观察,再画出对称图形。
2.下面的图形是对称图形吗?如果是,画出它的对称轴。
3.在点子图上画出你喜欢的对称图形。
4.画出所有的对称轴。
参考答案一.选择题1.B2.A3.B4.A5.A;B二.判断题1.×2.√3.×4.×5.×三.填空题1.旋转;平移2.13.平移;旋转4.25.△;□;△;□四.作图题1.如图所示:2.是对称图形。
有1条对称轴。
3.如图:4.如下:。
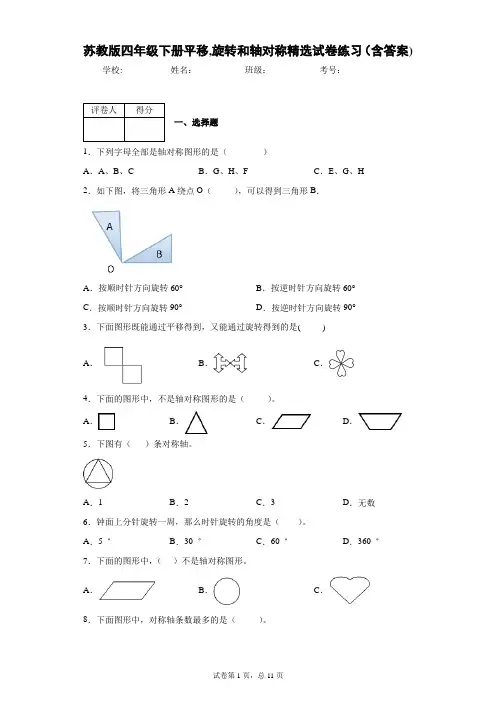
苏教版四年级下册平移,旋转和轴对称精选试卷练习(含答案) 学校:___________姓名:___________班级:___________考号:___________评卷人得分一、选择题1.下列字母全部是轴对称图形的是()A.A、B、C B.G、H、F C.E、G、H2.如下图,将三角形A绕点O(),可以得到三角形B.A.按顺时针方向旋转60°B.按逆时针方向旋转60°C.按顺时针方向旋转90°D.按逆时针方向旋转90°3.下面图形既能通过平移得到,又能通过旋转得到的是( )A.B.C.4.下面的图形中,不是轴对称图形的是()。
A.B.C.D.5.下图有()条对称轴。
A.1 B.2 C.3 D.无数6.钟面上分针旋转一周,那么时针旋转的角度是()。
A.5゜B.30゜C.60゜D.360゜7.下面的图形中,()不是轴对称图形。
A.B.C.8.下面图形中,对称轴条数最多的是()。
A.B.C.D.9.从6:00到6:30,分针旋转了()A.30°B.90°C.180°10.下列图形中,不是轴对称图形的是()。
A.正方形B.梯形C.圆11.下图中有三个三角形,说法正确的是().A.将三角形A向右平移2格可以得到三角形BB.将三角形B向右平移8格可以得到三角形CC.将三角形B向左平移8格可以得到三角形A评卷人得分二、作图题12.按要求画出下列图形。
把四边形绕点A顺时针旋转90°。
②把三角形绕点B逆时针旋转90°,再把旋转后图形向右平移5格。
③把最右边的图形补全,使它成为轴对称图形。
13.(1)把梯形ABCD划分成2个三角形,使它们的面积比是1:2.(2)梯形ABCD是一个轴对称图形的一半,请以BC边所在的直线为对称轴,画出这个轴对称图形的另一半.(3)将梯形ABCD绕A点顺时针旋转90°.画出旋转后的图形.旋转后D点的对应点用数对表示为().14.(1)将下图中三角形先向右平移5格,再向下平移4格。

专题9:平移、旋转和轴对称2022—2023年三年级数学暑假专项提升(西师大版)本专题主要针对平移、旋转和轴对称的内容进行逐层巩固拔高拓展,包括:1、平移和旋转的意义2、平移和旋转的判断3、轴对称的认识和特点4、平移、旋转和轴对称的应用一、选择题1.下面属于平移现象的是()。
A.秒针的转动B.行驶中的汽车轮子C.起重机吊起货物2.下列图形哪一个不是轴对称图形?()A.B.C.D.3.下面现象不属于旋转的是().A.B.C.4.下列物体只做旋转的是()。
A.钟表的指针B.坠落的铁球C.吊车把货物吊到高空5.下面不是旋转现象的是()A.抽陀螺B.玩风车C.吹风扇D.写字6.小汽车在平直的马路上行驶时,车身的运动属于()。
A.平移B.旋转C.对称7.把一张圆形的纸对折,再对折,再对折,所形成的角是()度。
A.30B.45C.908.下列图形一定是轴对称图形的()A.锐角三角形B.平行四边形C.圆形D.梯形9.图形绕点O顺时针旋转180°得到的图形是()。
A.B.C.D.10.一个正方形最多可以画()条对称轴.A.1B.4C.2二、填空题11.下面现象中,_____是平移,_____是旋转.12.一个正方形最多可以画________条对称轴.13.看图填空(1)上图中点A和点________到对称轴的距离都是2格.(2)点B和点B′到对称轴的距离都是________格.(3)点________和点________到对称轴的距离都是5格14.欣赏下面美丽的图形,你知道它们分别是由哪个图形通过旋转或平移形成的?这个图形是由________。
一、填空题1.升国旗时,国旗上升是_______现象;钟面上时针沿顺时针方向走动是_______现象。
(填“平移”或“旋转”)2.⑴蜡烛向_________平移了________格.⑴小鱼向________平移了________格.3.升旗时红旗的上升是_______现象;汽车行驶时车轮的转动是_______ 现象。
苏教版数学三年级上册单元测试卷第六单元平移、旋转和轴对称学校:___________姓名:___________班级:___________考号:___________一、选择题1.图b是由图a经过()变换得到的。
A.平移B.旋转C.轴对称2.下面属于旋转现象的是()。
A.用卷笔刀削铅笔B.从滑梯顶部滑下C.把晾晒的衣物从绳子的左边推到右边D.不小心将书掉在地上3.如图的图像绕虚线旋转一周,可以得到的几何体是()。
A.B.C.D.4.图形在平移或旋转后,()变了。
A.形状B.大小C.位置D.方向5.下面的图形中,()不是轴对称图形。
A.B.C.D.6.下列图案是几种汽车的标志,其中轴对称图形有()个。
A.2个B.3个C.4个D.5个7.把三角形在方格纸上先向下平移2格,再向右平移6格,再向下平移2格的位置()。
A.相同B.不相同C.不一定相同D.无法确定8.下面每组中的两个图形经过平移后,可以互相重合的是()。
A.B.C.D.9.下列属于旋转现象的是()。
A.汽车方向盘的运动B.拉开抽屉C.电梯的运动D.升国旗10.下面的第一个图形是通过()变成第二个图形的。
A.旋转B.平移C.对称11.是从下面哪张对折后的纸上剪下来的?正确的是()。
A.B.C.12.下面的字母中()不是轴对称图形。
A.W B.X C.Y D.Z13.下列物体的运动方式中,()与其他三种运动方式不同。
A.抽屉运动B.螺旋桨运动C.钟摆摆动D.风扇叶片转动14.将旋转一周后得到的立体图形是()。
A.B.C.D.二、填空题15.平移不改变图形的______和______,只改变图形的______16.小船先向____移了____格,又向____平移了____格。
17.图形经过平移后,( )不变,( )发生了改变。
18.风车的运动是( )现象,打开车窗是( )现象。
19.下列图形中,哪些是对称的,在括号里打“√”。
20.如图的哪个图案是通过平移左面的图案得到的?请画“√”。
(苏教版)三年级数学上册《平移、转动、
轴对称》练习题
一、选择题
1. 在以下选项中,哪一项是体现了平移的图形?
a) 一个圆被移到另一个位置
b) 一个圆被旋转了一下
c) 一个圆变得更大了
d) 一个圆被镜像了一下
2. 下图中哪个图形是轴对称图形?

a) 图形A
b) 图形B
c) 图形C
d) 图形D
3. 在以下选项中,哪一项是体现了转动的图形?
a) 一个三角形被翻了一个方向
b) 一个三角形被移到另一个位置
c) 一个三角形的角度变大了
d) 一个三角形被旋转了一下
二、填空题
1. 对于一个图形的平移,图形的形状、大小、方向是不变的,
只是位置 _______。
2. 图形A是图形B的轴对称图形,当把图形A沿着轴对称线
翻折后,与图形B _______。
3. 在转动中,图形终点的位置与起点的位置 _______。
三、判断题
1. 一个图形的轴对称图形与原图形的大小、形状、方向都相同。
(√ / ×)
2. 只有正方形可以是轴对称图形。
(√ / ×)
3. 轴对称是指一个图形关于某条轴翻折后,两端重合。
(√ / ×)
四、解答题
1. 请解释什么是平移,转动和轴对称。
2. 请举例说明平移、转动和轴对称在日常生活中的应用。
以上是《平移、转动、轴对称》的练习题,请仔细阅读题目,认真思考后给出答案。
祝你学习进步!。
轴对称、平移与旋转测试题(含答案)一、选择题(本大题共7小题,每小题5分,共35分;在每小题给出的四个选项中,只有一项符合题意)1.国产越野车“BJ40”中,哪个数字或字母既是中心对称图形又是轴对称图形( ) A.B B.J C.4 D.0图12.如图1,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B 的度数为( )A.48°B.54°C.74°D.78°3.将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平,你可以看到的图形是( )图24.如图3,在△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且点C′在BC上,则∠B′C′B的度数为( )A.56° B.50° C.46° D.40°图3 图45.如图4所示,将边长为2 cm的等边三角形ABC沿BC的方向向右平移1 cm得到△DEF,则四边形ABFD的周长为( )A.6 cm B.8 cm C.10 cm D.12 cm6.4张扑克牌如图5①所示放在桌面上,小敏把其中一张牌旋转180°得到图②,那么她所旋转的牌是从左数( )图5A.第一张 B.第二张 C.第三张 D.第四张7.下列说法正确的有( )图6(1)全等图形的面积相等,反过来,面积相等的两个图形是全等图形;(2)如图6所示的两个图形,放在一起能完全重合,但是图甲和图乙不全等;(3)如图7所示,△ABC与△DEF 是全等的,点A与点D是对应点,点B与点E是对应点,所以可以记为:△ABC≌△DEF;(4)如果两个图形的形状一样,大小一样,那么它们是全等图形.图7A.1个 B.2个 C.3个 D.4个二、填空题(本大题共7小题,每小题5分,共35分)8.如图8,下列各组图形中,由左边变成右边的图形,分别进行了平移、旋转、轴对称、中心对称等变换,其中进行平移变换的是________,进行旋转变换的是________,进行轴对称变换的是________,进行中心对称变换的是________.(填序号)图89.如图9所示,在正方形网格中,格点三角形DEF是由格点三角形ABC平移得到的,则点B向右移动了________格.图910.如图10所示,大长方形的长为8 cm,宽为4 cm,则阴影部分的面积是________.图1011.如图11,将长方形纸片ABCD的一角沿EF折叠,使点C落在长方形ABCD的内部点C′处.若∠EFC=35°,则∠DEC′=________°.图11 图1212.如图12是4×4的正方形网格,其中已有3个小方格涂成了黑色.现要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案是轴对称图形,这样的白色小方格有________个.13.数轴上的点A表示-2,将数轴上到点A的距离为3的点B向右平移5个单位长度得到点C,再把点C绕点A旋转180°得到点D,则AD的长为________.图1314.如图13,在直角三角形ABC中,∠ACB=90°,∠A=α,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的度数为________.三、解答题(本大题共3小题,共30分)15.(8分)在如图14所示的网格中有四边形ABCD.(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称?若对称,请在图中画出对称轴或对称中心.图1416.(10分)如图15所示,在△ABC中,∠C=90°,将△ABC沿直线DE对折,点B刚好与点A重合,连结AD,∠DAE与∠DAC的度数之比为2∶1,求∠B的度数.图1517.(12分)取一副三角尺按图16①所示的方式放在一起,∠ACD=30°,∠BAC=45°,固定三角尺ADC,将三角尺ABC以点A为中心按顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△ABC′,如图②所示.(1)当α为多少度时,能使得AB∥DC?(2)连结BD,当0°<α≤45°时,探究∠DBC′+∠CAC′+∠BDC的值的大小变化情况,并说明理由.图16教师详解详析1.[解析] D A.B不是中心对称图形,是轴对称图形,故本选项错误;B.J不是中心对称图形,也不是轴对称图形,故本选项错误;C.4不是中心对称图形,也不是轴对称图形,故本选项错误;D.0既是中心对称图形又是轴对称图形,故本选项正确.2.[答案] B3.[答案] C4.[解析] C∵点C′在边BC上,∴∠BC′C为平角.由于旋转不改变图形的大小,∴∠AC′B′=∠C=67°,AC′=AC,∴∠AC′C=∠C=67°,∴∠B′C′B=180°-∠AC′C-∠AC′B′=180°-67°-67°=46°.5.[解析] B由题意知△ABC≌△DEF,AD=BE=1 cm,DF=AC=2 cm,四边形ABFD的周长=AB+BF+DF+AD=8 cm.6.[答案] A7.[答案] B8.[答案] ③①④②④9.[答案] 5[解析] 注意点B的对应点是点E,从点B到点E向右平移了5格.10.[答案] 8 cm2[解析] 通过平移、旋转,可知阴影部分的面积是大长方形总面积的错误!.11.[答案] 7012.[答案] 413.[答案] 8或2[解析] 数轴上到点A的距离为3的点表示的数有两个:1和-5,向右平移5个单位长度得到的数分别是6和0,所以AC绕点A旋转180°得AD=8或2.14.[答案] 2α15.解:(1)四边形A1B1C1D1如图所示.(2)四边形A2B2C2D2如图所示.(3)四边形A1B1C1D1与四边形A2B2C2D2对称,对称轴为图中的直线EF.16.解:由翻折的性质知,DE平分∠ADB,所以∠ADE=∠BDE,∠DAB=∠B.又因为∠DAE与∠DAC的度数之比为2∶1,所以设∠DAC=x°,则∠B=∠DAB=2x°.因为∠C=90°,根据三角形的内角和为180°,得x°+2x°+2x°=90°,解得x=18,所以∠B=36°.17.解:(1)由题意得∠CAC′=α,要使AB∥DC,须∠BAC=∠ACD=30°,∴α=∠CAC′=∠BAC′-∠BAC=45°-30°=15°,即α=15°时,能使得AB∥DC.(2)如图,连结BD,∠DBC′+∠CAC′+∠BDC的值的大小没有变化,总是105°.理由:当0°<α≤45°时,总有△EFC′存在.∵∠EFC′=∠BDC+∠DBC′,∠CAC′=α,∠FEC′=∠CAC′+∠C,∠EFC′+∠FEC′+∠C′=180°,∴∠BDC+∠DBC′+∠C+α+∠C′=180°.又∵∠C′=45°,∠C=30°,∴∠DBC′+∠CAC′+∠BDC=105°.。
苏教版四年级数学下册单元综合素质评价第一单元平移、旋转和轴对称一、填空。
(第5题每空2分,其余每空1分,共30分)1.欣赏下面图形,它们分别是通过什么变换得到的?(填“平移”或“旋转”)( ) ( ) ( ) ( ) 2.钟面上的分针从3:30到3:45,按( )时针方向旋转了( )°。
3.正方形有( )条对称轴,长方形有( )条对称轴,圆有( )条对称轴。
4.寓意深远的汉字文化中也蕴含着数学的美,在“昌、日、比、台、正、全”这些汉字中,有( )个轴对称的字。
5.下面的物体是向哪个方向平移的?(1)飞机向( )平移(2)汽车向( )平移6.观察下图,图形①绕点O顺时针旋转90°到图形( )所在的位置,图形( )绕点O( )时针旋转90°到图形③所在的位置。
7.如果上图中把葡萄从托盘中拿下来,指针会( )时针旋转( )°。
8.体育课上,当老师喊“立正,向左转”时,你的身体( )时针旋转( )°;当老师喊“立正,向右转”时,你的身体( )时针旋转( )°。
9.右图中:(1)图形B向下平移可以得到图形( )。
(2)图形F绕点N逆时针旋转180°得到图形( )。
(3)图形A绕点M顺时针旋转90°得到图形( )。
(4)图形E绕点M逆时针旋转90°得到图形( )。
(5)与图形C可以组成轴对称图形的是图形( )、( )和( )。
二、选择。
(将正确答案的字母填在括号里)(每小题2分,共12分)1.每年12月2日是全国交通安全日。
下列交通标志中,是轴对称图形的有( )个。
A.2 B.3 C.4 D.52.下图是一个电风扇开关,数字表示风速档。
现在风扇在“1”档运行,如果要关闭,可将旋钮( )。
A.按顺时针方向旋转90°B.按顺时针方向旋转120°C.按逆时针方向旋转90°D.按逆时针方向旋转120°3.把任意一个图形绕任意点顺时针旋转( ),又回到了原来的位置。
平移、旋转与轴对称练习
1.将图1所示的图案通过平移后可以得到的图案是( )
2、如图,在55⨯方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A .先向下平移3格,再向右平移1格;
B .先向下平移2格,再向右平移1格
C .先向下平移2格,再向右平移2格;
D .先向下平移3格,再向右平移2格
3、下列四个图案中,可以通过右图平移得到的是( )
4、如图,将边长为2个单位的等边△ABC 沿边BC 向右平移1个单位得到△DEF ,则四边形ABFD 的周长为( )
A .6
B 。
8 C. 10 D.12. 5、将线段AB 平移1cm ,得到线段A B '',则对应点A 与A '
的距离为
_____________cm .
6、下列几何图形中,即是中心对称图形又是轴对称图形的是( )
A .正三角形
B .等腰直角三角形
C .等腰梯形
D .正方形
7、下列图形中,既是轴对称图形,又是中心对称图形的是( ).
8、观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )
A .1个
B .2个
C .3个
D .4个
9、下列图形中,既是轴对称图形又是中心对称图形的有( )
A .4个
B .3个
C .2个
D .1个
10、下列图形中,中心对称图形有( ).
A .1个
B .2个
C .3个
D .4个
11、下列图形中既是轴对称图形,又是中心对称图形的是( )
A .
B .
C .
D .
. B . C . D .
12、右上图中,不是中心对称图形的是( )
13、已知如图1所示的四张牌,若将其中一张牌旋转180O 后得到图2,则旋转的牌是( )
9、把下列每个字母都看成一个图形,那么中心对称图形有( )
E H I N A
A 2个
B 3个
C 4个
D 5个
10、如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A .1组
B .2组
C .3组
D .4组
11、我们已经学习了:①等边三角形;②等腰梯形;③平行四边形;④等腰三角形;⑤圆.在
以上五种几何图形中,既是轴对称图形,又是中心对称图形的是 .
12、如图,已知BC 为等腰三角形纸片ABC 的底边,90AD BC BAC ⊥∠≠,°.将此三角形纸片沿AD 剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出中心对称图形 个.
13、图①、图②均为76⨯的正方形网格,点A B C 、、在格点上.
(1)在图①中确定格点D ,并画出以A B C D 、、、为顶点的四边形,使其为轴对称图形.(画一个即可)
① ② ③ ④ A B C D
图1
图2
、、、为顶点的四边形,使其为中心对称(2)在图②中确定格点E,并画出以A B C E
图形.(画一个即可)
14、如图,△ABC与△A`B`C`关于直线l对称,且∠A=78°,∠C`=48°,
则∠B的度数为()
A.48°B.54°C.74°D.78°
15、下列四个图形中,不是轴对称图形的是()
A.B.C.D.
16、下列图形是轴对称图形是()
17、如下书写的四个汉字,其中为轴对称图形的是( ).
A.B. C. D.
18、将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线(直角三角形的中位线)
剪去上面的小直角三角形
将留下的纸片展开,得到的图形是()
A.B.C.D.
19、下列图形中,轴对称图形的个数是().
A.1B.2C.3D.4
20、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们
把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是()
A.对应点连线与对称轴垂直B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分D.对应点连线互相平行
21、请写出一个是轴对称图形的图形名称.答:.
22、从下列图形中是轴对称图形的为。
23、如图,镜子中号码的实际号码是___________ .
24、星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)
的位置如图所示,此时时针表示的时间是.(按12小时制填写)
25、已知图形B是一个正方形,图形A由三个图形B构成,如图所示,请用图形A与B合
拼成一个轴对称图形并车出来。
26、一节课45分钟,钟表的时针转过的角度是______.
27、用一具三角板(含30°,45°,60°)能作出大于0°而小于180°的角共有()
A.4个B.6个C.11个D.13个
28、若∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的三分之一,那么∠1、∠2、∠
3的度数分别为()
A.75○、15○、105○B、60○、30○、120○C.50○、40○、130○D、70○、20○、110○29、已知αβ是两个钝角,计算(α+β)的值,四个同学四种不同的答案分别是24°,148°,276°,
386°,其中只有一个答案是正确的,则正确的答案是()A.386°B.276°C.148°D.24°30、甲同学看乙同学的方向为北偏东60°则乙同学看甲同学的方向为()
A.南偏东30°B.南偏西60°C.东偏南60°D.南偏西30°
31、5点20分时,时钟的时针和分针的夹角为()
A.30°B.40°C.45°D.50°
32、如图1―4-5所示,AC为一条直线,O是AC上
一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC,.
(1)求∠EOF的大小;
(2)当OB绕O旋转时,OE、OF仍为∠AOB和∠BOC平分线,
问:OF、OF有怎样的位置关系?你能否用一句话概括出这个命题.
33、下列说法中,正确的是()
A.一个角不是锐角必是钝角B.90°的角叫余角,180°的角叫补角
C.如果一个角有余角,则这个角必是锐角D.如果一个角是补角,则这个角必
是钝角
34、.将一长方形纸片,按图l-4-6的方式折叠,BC、BD为折痕,
则∠CBD的度数为()
A.60°B.75°C.90°D.95°
35、已知∠α和∠β互为补角,且∠β的一半比∠α小30°,求∠α和∠β
36、小亮在镜中看到身后墙上的时钟如图1―4―7所示,你认为实际时间最接近八点的是()
37、将一正方形纸片按如图1―4―8中⑴、⑵的方式依次对折后,再沿⑶中的虚线裁剪,最后将⑷中的纸片打开铺平,所得图案应该是图如图1―4―9中的()
38、用一副三角板可以直接得到30°,45°,60°,90°,四种角,利用一副三角板可以拼出另外一些特殊角,如75°,120°等,请你拼一拼,使用一副三角板还能拼出哪些小于平角的角?这些角的度数是_________.。