下载文档原格式
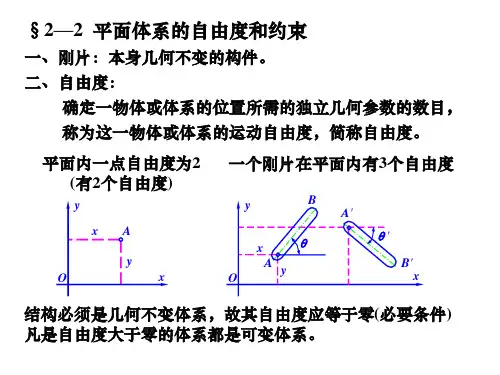
平面体系自由度和约束自由度：所谓体系的自由度，是指该体系运动时，用来确定其位置所需的独立坐标（或参变量）的个数。
如果一个体系的自由度大于零，则该体系就是几何可变体系。
（1）点的自由度：平面内一动点A，其位置需用两个坐标x和y来确定，所以一个点在平面内有两个自由度。
1.swf（2）刚片的自由度：一个刚片在平面内运动时，其位置将由其上任一点A的坐标x、y 和过点A的任一直线AB的倾角φ来确定，因此，一个刚片在平面内有三个自由度。
2.swf约束：约束是指能够减少自由度的装置（又称联系）。
减少一个自由度的装置，就称为一个约束（或联系）。
约束有两大类：支座约束和刚片间的约束。
1. 支座约束（1）滚轴支座：能限制刚片A点在垂直方向移动，但不能限制其水平方向移动和绕A 点的转动，减少了一个自由度，相当于一个约束。
3.swf（2）铰支座：能限制刚片A点在水平方向和竖直方向移动，但不能限制其绕A点的转动，减少了两个自由度，相当于两个约束。
4.swf（3）固定支座：能限制刚片在水平、竖直方向的移动和转动，使刚片的自由度减少为零，相当于三个约束。
5.swf2. 刚片间的联结约束（1）单铰约束：联结两个刚片的铰称为单铰。
两刚片在平面内独立的自由度个数为六个，用一个铰将刚片Ⅰ、Ⅱ联结起来，对刚片Ⅰ而言，其位置可由A点的坐标x、y和AB 线的倾角φ1来确定，因此其有三个自由度，刚片Ⅱ相对刚片Ⅰ只能绕A点转动，即两刚片间只保留了相对转角φ2，则由刚片Ⅰ、Ⅱ所组成的体系在平面内有四个自由度，则一个单铰约束减少了二个自由度。
一个单铰相当于两个约束。
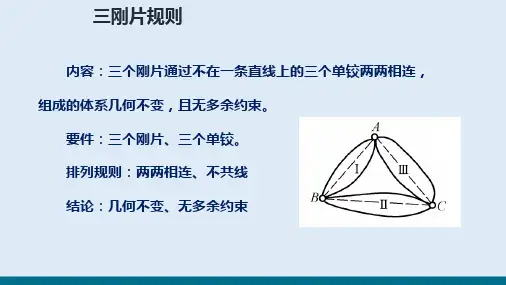
6.swf（2）复铰约束：用一个铰同时联结三个或三个以上的刚片，则这种铰称为复铰。
设其中一刚片可沿x、y向移动和绕某点转动，则其余两刚片都只能绕其转动，因此各减少两个自由度。
象这种联结三刚片的复铰相当于两个单铰的作用，由此可见，联结n个刚片的复铰，相当于（n－1）个单铰的作用。
7.swf。
平面体系的计算自由度 W 的求法
（1）刚片法：体系看作由刚片组成，铰结、刚结、链杆为约束。
刚片数 m ；
约束数：单铰数 h ，简单刚结数 g ，单链杆数 b 。
W = 3m - 2h - 3g -b
（2）节点法：体系由结点组成，链杆为约束。
结点数 j ；
约束数：链杆（含支杆）数 b 。
W = 2j – b
（3）组合算法
约束对象：刚片数 m ，结点数 j
约束条件：单铰数 h ，简单刚结数 g ，单链杆（含支杆）数 b
W = （3m + 2j）-（3+2h+ b）
比较可得：三铰拱与简支梁的竖向支反力完全相同。
注意到水平支反
力式中的分子就是简支梁上截面C的弯矩，则水平支反力可写作：
综上所述，三铰拱在竖向荷载作用下，任一截面上的弯矩、剪力荷轴力的计算公式如下：
4.4.1 各种结构位移计算公式
：虚设单位荷载P=1作用下的结构的内力；
：实际荷载作用下的结构的内力
图乘法
位移公式：
4.5.2 常见图形的面积和形心
常见图形的形心和面积（图4.10）。
图4.10
以上图形的抛物线均为标准抛物线：抛物线的顶点处的切线都是与基线平行
4.5.3 应用图乘法时的几个具体问题
(2) 如果有一个图形为折线，则应分段考虑（图4.12）
图4.12
(3) 如果图形比较复杂，应根据弯矩图的叠加原理将图形分解为几个简单图形，分项计算后再进行叠加图4.13
图4.13
（图4.13b中A1与y1的乘积为负值；图4.13c中抛物线为非标准曲线）。
例5：试求出图4.16刚架结点B 的水平位移和转角，EI 为常数。
