2.3 平面体系的计算自由度
- 格式：ppt
- 大小：185.50 KB
- 文档页数：11
下载文档原格式
合集下载
结构力学章节习题及参考答案
第3章静定梁与静定刚架习题解答
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。（ ）
(2) 区段叠加法仅适用于弯矩图的绘制，不适用于剪力图的绘制。（ ）
(3) 多跨静定梁在附属部分受竖向荷载作用时，必会引起基本部分的内力。（ ）
(4)习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。（ ）
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。（ ）
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i，欲使结点B产生顺时针的单位转角，应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构（EI=常数）时，传递系数CBA=________，CBC=________。
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。（ ）
(2) 区段叠加法仅适用于弯矩图的绘制，不适用于剪力图的绘制。（ ）
(3) 多跨静定梁在附属部分受竖向荷载作用时，必会引起基本部分的内力。（ ）
(4)习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。（ ）
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。（ ）
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i，欲使结点B产生顺时针的单位转角，应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构（EI=常数）时，传递系数CBA=________，CBC=________。
平面机构自由度
(2)自由度计算： n=8
Pl=11
F=3×8 - 2×11 – 1=1
Ph=1 机械设计基础
平面机构的自由度
例2 计算如图所示大筛机构的自由度
解：(1)分析特殊自由度情况 复合铰链 虚约束
局部自由度
(2)自由度计算： F 37 29 1 2
机械设计基础
平面机构的自由度
例3 求图示机构 的自由度
B处转动副数：3−1=2
F 3n 2 pl ph 35 27 0 1
机械设计基础
平面机构的自由度
局部自由度 —— 不影响整个机构运动的局部的独立运动
局部自由度
滚子本身的转动自由度 不影响其它构件的运动规律，故 称其为局部自由度。
计算时的处理： 把滚子看成与从动件
固接一体，消除局部自由度 后，再计算机构自由度。
图示的转动副约束了x、 y两个方向的移动, 只保留一个转动；
机械设计基础
平面机构的自由度
图示的移动副约束了沿y轴方向 的移动和在xOy平面内的转动, 只保留沿x轴方向的移动；
图示的高副只约束了沿接触 处公法线n-n方向的移动。
机械设计基础
平面机构的自由度
3、 平面机构自由度的计算 计算公式
机构的自由度就是机构具有独立运动参数的数目。 自由度取决于运动链中构件的数目及运动副的类型和 数目。 设一个平面运动链由k个构件组成, 其中一个构件为机架, 则有n=k-1个活动构件。 未构成运动副之前, 这些活动 构件应有3n个自由度。 假设构成PL个低副和PH个高副, 而一个低副引入两个约束, 一个高副引入一个约束, 每 引入一个约束构件就失去一个自由度, 故整个运动链相 对机架的自由度应为活动件自由度的总数与运动副引 入约束总数之差。 以F表示机构的自由度数, 则有
清华大学结构力学第2章几何构造分析34
II
17
5. 关于无穷远瞬铰的情况
1 C II
I A
2
a)
B
III
一个瞬铰C在无穷远处，铰A、B连线与形成 瞬铰的链杆1、2不平行，故三个铰不在同一直 线上，该体系几何不变且无多余约束（图a）。
18
A B
I II C
b)
III 瞬铰B、C在两个不同方向的无穷远处，它 们对应于无穷线上两个不同的点，铰A位于 有限点。由于有限点不在无穷线上，故三铰 不共线，体系为几何不变且无多余约束（见 图b）。
一、复杂链杆与复杂铰
1. 简单链杆与复杂链杆 简单链杆——仅连接两个结点的链杆称为简
单链杆，一根简单链杆相当于一个约束。
复杂链杆——连接三个或三个以上结点的链杆
称为复杂链杆。一根复杂链杆相当于（2n-3） 根简单链杆，其中n为一根链杆连接的结点数。
35
2. 简单铰与复杂铰 简单铰——只与两个刚片连接的铰称为简单铰。
19
A I II
c)
B III C
形成瞬铰B、C的四根链杆相互平行（不等 长），故铰B、C在同一无穷远点，所以三个 铰A、 B、C位于同一直线上，故体系为瞬变 体系（见图c）。
20
6. 装配格式和装配过程
基本装配（建造、施工）格式
把一个节点固定到一个刚片上；
把一个刚片固定到另一个刚片上；
把两个刚片固定到另一个刚片上。
9
3
I
解: 用混合公式计算。 m=1 j=5 g=2 b=10
W (3 1 2 5) (3 2 10)
13 16 3
41
例2-3-5 求图示体系的计算自由度。
1 2 4 A 3 B 5 6 E 7 C 8 D 10 11
17
5. 关于无穷远瞬铰的情况
1 C II
I A
2
a)
B
III
一个瞬铰C在无穷远处，铰A、B连线与形成 瞬铰的链杆1、2不平行，故三个铰不在同一直 线上，该体系几何不变且无多余约束（图a）。
18
A B
I II C
b)
III 瞬铰B、C在两个不同方向的无穷远处，它 们对应于无穷线上两个不同的点，铰A位于 有限点。由于有限点不在无穷线上，故三铰 不共线，体系为几何不变且无多余约束（见 图b）。
一、复杂链杆与复杂铰
1. 简单链杆与复杂链杆 简单链杆——仅连接两个结点的链杆称为简
单链杆，一根简单链杆相当于一个约束。
复杂链杆——连接三个或三个以上结点的链杆
称为复杂链杆。一根复杂链杆相当于（2n-3） 根简单链杆，其中n为一根链杆连接的结点数。
35
2. 简单铰与复杂铰 简单铰——只与两个刚片连接的铰称为简单铰。
19
A I II
c)
B III C
形成瞬铰B、C的四根链杆相互平行（不等 长），故铰B、C在同一无穷远点，所以三个 铰A、 B、C位于同一直线上，故体系为瞬变 体系（见图c）。
20
6. 装配格式和装配过程
基本装配（建造、施工）格式
把一个节点固定到一个刚片上；
把一个刚片固定到另一个刚片上；
把两个刚片固定到另一个刚片上。
9
3
I
解: 用混合公式计算。 m=1 j=5 g=2 b=10
W (3 1 2 5) (3 2 10)
13 16 3
41
例2-3-5 求图示体系的计算自由度。
1 2 4 A 3 B 5 6 E 7 C 8 D 10 11
平面自由度计算
典型例题三
6
1
2 5
4
3
计算图示机构自由度。 分析：该机构具有5个 活动构件，有7个转动 副，即低副，没有高 副。于是机构自由度 为
F=3n-2 p5 – p4=3×5 - 2×7-0=1
机构的自由度与确定运动条件
四、机构具有确定运动的条件
◆问题：取运动链中某个构件为机架，即构成 机构，那么机构在什么条件下才具有确定运动？
机构中某些构件所产生的局部运动并不影响其他构件的运 动, 把这种局部运动的自由度称为局部自由度。数目用f′表示.
机构的自由度与确定运动条件
计算机构自由度应注意的事项（续）
★ 虚约束
指机构在某些特定几何条件或结构条件下，有些运动 副带入的约束对机构运动实际上起不到独立的约束作用, 这些对机构运动实际上不起约束作用的约束称为虚约束， 用P′表示。
束作用,其它各处均为 虚约束;
机构的自由度与确定运动条件
计算机构自由度应注意的事项（续）
3. 若两构件在多处相接触构成平面高副，且各接触点处 的公法线重合,则只能算一个平面高副。若公法线方向不 重合，将提供各2个约束。
n=2 P5=2 P4=1 F=3n-(2P5+P4)=3*2-2*2-1=1
有一处为虚约束
小结
存在于转动副处
◆ 复合铰链
正确处理方法：复合铰链处有m个构件 则有(m-1)个转动副
◆局部自由度
常发生在为减小高副磨损而将滑动摩擦 变成滚动摩擦所增加的滚子处。
正确处理方法：计算自由度时将局部自 由度减去。
◆ 虚约束
存在于特定的几何条件或结构条件下。
正确处理方法：将引起虚约束的构件和 运动副除去不计。
用瞬心法作机构的速度分析
6
1
2 5
4
3
计算图示机构自由度。 分析：该机构具有5个 活动构件，有7个转动 副，即低副，没有高 副。于是机构自由度 为
F=3n-2 p5 – p4=3×5 - 2×7-0=1
机构的自由度与确定运动条件
四、机构具有确定运动的条件
◆问题：取运动链中某个构件为机架，即构成 机构，那么机构在什么条件下才具有确定运动？
机构中某些构件所产生的局部运动并不影响其他构件的运 动, 把这种局部运动的自由度称为局部自由度。数目用f′表示.
机构的自由度与确定运动条件
计算机构自由度应注意的事项（续）
★ 虚约束
指机构在某些特定几何条件或结构条件下，有些运动 副带入的约束对机构运动实际上起不到独立的约束作用, 这些对机构运动实际上不起约束作用的约束称为虚约束， 用P′表示。
束作用,其它各处均为 虚约束;
机构的自由度与确定运动条件
计算机构自由度应注意的事项（续）
3. 若两构件在多处相接触构成平面高副，且各接触点处 的公法线重合,则只能算一个平面高副。若公法线方向不 重合，将提供各2个约束。
n=2 P5=2 P4=1 F=3n-(2P5+P4)=3*2-2*2-1=1
有一处为虚约束
小结
存在于转动副处
◆ 复合铰链
正确处理方法：复合铰链处有m个构件 则有(m-1)个转动副
◆局部自由度
常发生在为减小高副磨损而将滑动摩擦 变成滚动摩擦所增加的滚子处。
正确处理方法：计算自由度时将局部自 由度减去。
◆ 虚约束
存在于特定的几何条件或结构条件下。
正确处理方法：将引起虚约束的构件和 运动副除去不计。
用瞬心法作机构的速度分析
结构力学 平面体系的几何构造分析
1
A
I
II
A
1
32
I
12
§2-2 几何不变体系的组成规律
3.三个刚片之间的连接
规则4：三个刚片用三个不共线的铰两两相连，则组成几何不 变体系且无多余约束。（三片三铰规则）
B
II A
B Ⅲ C
I
注：三个刚片之间的连接铰可 以是实铰亦可以是虚铰
I
III
A
II C
13
§2-2 几何不变体系的组成规律
4.当规则中的限制条件不被满足时则体系为瞬变或常变。
5
§2-1 几何构造分析的基本概念
y
y
xφ
2 3
x 1
x,
x
y
x,y,1,2,3x
单链杆约束
y
复链杆约束 n—结点个数
x
6
§2-1 几何构造分析的基本概念
2）铰 ①单铰约束：连结两个刚片的铰称为单铰。
结论：一个单铰可减少两个自由度，相当于两个约束或联系，相当于两 根单链杆的作用。 ②复铰： 连结两个以上刚片的铰称为复饺。
例2-3-1 试求图示体系的计算自由度。
AI
II
C III
B1
2
3
解： m3 g0 h3 b3
W33(233)990
另解： m3,g0,h2,b5 W33302250
30
§2-3 平面杆件体系的计算自由度
例2-3-2 求体系的计算自由度W W=3m-2h-b =3*7-2*9-3=0 W=2j-b=2*7-14=0
23
§2-2 几何不变体系的组成规律
例2-2-2 试分析图示体系的几何构造。 解：
刚片I、II用链杆1、2相连 （瞬铰A) 刚片I、III用链杆3、4相连（瞬铰B)
2-3 平面杆件体系的计算自由度
§2-3 平面杆件体系的计算自由度1. 教学要求掌握实际自由度和计算自由度的计算方法。
2. 本节目录•1. 实际自由度S和计算自由度W•2. 部件和约束•3. 平面体系的计算自由度W的求法(1)•4. 平面体系的计算自由度W的求法(2)•5. 思考与讨论3. 参考章节1.《结构力学教程(Ⅰ)》，pp.28-32。
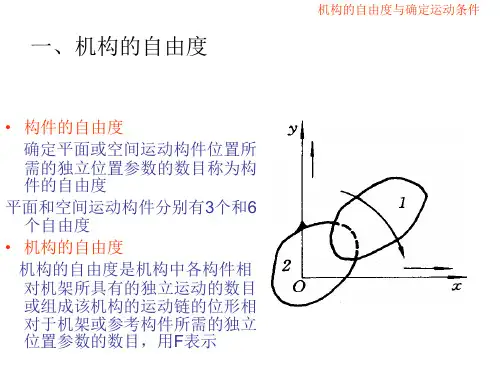
2. §2-1 基本概念2.3.1 实际自由度S 和计算自由度WS= （各部件自由度总和a）－（非多余约束数总和c）--- (2-1)S：体系是由部件加上约束组成的。
首先假设体系中各个约束都不存在，在此情况下计算各部件的自由度数的总和为a；其次在全部约束中确定非多余约束数c；最后将两个数相减得出体系的自由度数s。
图2-32S = 1×１－１= 0，非多余约束数 c = 2 ，多余约束数n = １，但是复杂情况难以找全多余约束。
在复杂体系中很难分清全部约束中哪些是多余约束和非多余约束。
因此引入计算自由度的概念W。
W = （各部件自由度总和 a ）－ （全部约束数总和 d ） --- (2-2)由于全部约束数d 与非多余约束c 的差数是多余约束n ，则 n W S =- （2－3）对于自由度S 与多余约束都不是负数即：0,0≥≥n S ，因此： W S ≥， W n -≥即W 是自由度数S 的下限，而－W 则是多余约束数n 的下限。
2.3.2 部件和约束1. 部件可以是点，也可以是刚片在几何构造分析时要注意刚片内部是否有多余约束。
图2-32a图2-32b 图2-32c 图2-32d 一根链杆 一个铰 一个刚结 n = 0n = 1n = 2n = 3在计算体系的约束总数时也应当考虑刚片内部的多余约束。
2. 约束可分为单约束和复约束在几何构造分析时要将复约束简化为几个单约束。
图2-33a图2-33b(图中复铰相当两个单铰)m = 2 , h = 1 m = 3 , h = 2S = 3 × 2 - 2 × 1 = 4S = 3 × 3 - 2 × 2 = 5图2-34a图2-34b(图中复刚结相当两个单刚结)m = 2 , g = 1m = 3 , g = 2S = 3 × 2 - 3 × 1 = 3S = 3 × 3 - 2 × 3 = 3结论1：一般说来，联结n 个刚片的复铰(复刚结)相当于(n-1)个单铰(单刚结)。
《结构力学》课后习题答案__重庆大学出版社
第1章 绪论（无习题）第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0，则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W ＜0，则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后，成为习题2.1(6) (b)图，故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后，成为习题2.1(6) (c)图，故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】（1）正确。
（2）错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
（3）错误。
（4）错误。
只有当三个铰不共线时，该题的结论才是正确的。
（5）错误。
CEF 不是二元体。
（6）错误。
ABC 不是二元体。
（7）错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。
平面体系的计算自由度
束的刚片，它们可以看作 在图a的刚片内部分别附加
了一根链杆或一个铰结或 c)
一个刚结。
All Rights Reserved
可编辑ppt
b)
d)
3
在应用公式时，应注意以下几点：
(3)刚片与刚片之间的刚结或铰结数目（复刚结或复 铰结应折算为单刚结或单铰结数目）计入g和h。
(4)刚片与地基之间的固定支座和铰支座不计入g和h， 而应等效代换为三根支杆或两根支杆计入r。
可编辑ppt
11
= 3×9-(3×3+2×8+6) = -4
可编辑ppt
5
【例2-2】试求图2-11所示体系的计算自由度。
m1
(1)g (1)h
m4
(1)h (1)g
m2
m6
(2)g (1)h
(2)g
m5
m8
m3
m7
(3)r
(3)r
m=9，g=6，r=9
(1)h
m9 (3)r
W = 3m-(3g+2h+r) = 3×9-(3×6+2×4+9) = -8
可编辑ppt
2
在应用公式时，应注意以下几点：
（1）地基是参照物，不计入m中。
（2）计入m的刚片，其内部应无多余约束。如果遇到内 部有多余约束的刚片，则应把它变成内部无多余约束的 刚片，而把它的附加约束在计算体系的“全部约束数”d 时考虑进去。
图a是内部没有多余约束的 刚片，而图b、c、d则是内
部分别有1、2、3个多余约 a)
All Rights Reserved
可编辑ppt
7
【例2-3】试求图2-12所示体系的计算自由度。
1
了一根链杆或一个铰结或 c)
一个刚结。
All Rights Reserved
可编辑ppt
b)
d)
3
在应用公式时，应注意以下几点：
(3)刚片与刚片之间的刚结或铰结数目（复刚结或复 铰结应折算为单刚结或单铰结数目）计入g和h。
(4)刚片与地基之间的固定支座和铰支座不计入g和h， 而应等效代换为三根支杆或两根支杆计入r。
可编辑ppt
11
= 3×9-(3×3+2×8+6) = -4
可编辑ppt
5
【例2-2】试求图2-11所示体系的计算自由度。
m1
(1)g (1)h
m4
(1)h (1)g
m2
m6
(2)g (1)h
(2)g
m5
m8
m3
m7
(3)r
(3)r
m=9，g=6，r=9
(1)h
m9 (3)r
W = 3m-(3g+2h+r) = 3×9-(3×6+2×4+9) = -8
可编辑ppt
2
在应用公式时，应注意以下几点：
（1）地基是参照物，不计入m中。
（2）计入m的刚片，其内部应无多余约束。如果遇到内 部有多余约束的刚片，则应把它变成内部无多余约束的 刚片，而把它的附加约束在计算体系的“全部约束数”d 时考虑进去。
图a是内部没有多余约束的 刚片，而图b、c、d则是内
部分别有1、2、3个多余约 a)
All Rights Reserved
可编辑ppt
7
【例2-3】试求图2-12所示体系的计算自由度。
1
《结构力学》课后习题答案__重庆大学出版社
第1章 绪论（无习题）第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0，则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W ＜0，则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后，成为习题2.1(6) (b)图，故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后，成为习题2.1(6) (c)图，故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】（1）正确。
（2）错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
（3）错误。
（4）错误。
只有当三个铰不共线时，该题的结论才是正确的。
（5）错误。
CEF 不是二元体。
（6）错误。
ABC 不是二元体。
（7）错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。
B-17 武汉理工大学 土木工程 结构力学 本科期末考试题解析
《结构力学》教学大纲一、本课程的性质与任务本课程为土木工程专业本科生的一门主要技术基础课。
通过本课程的教学，使学生了解杆件体系的组成规律，了解各类结构的受力性能，撑握杆件结构的计算原理和方法，培养分析与解决工程实际中杆系结构力学问题的能力，为学习后续有关专业课程以及将来进行结构设计和科学研究打下力学基础。
二、本课程的教学内容、基本要求及学时分配1．绪论（4学时）（1）教学内容1.1结构力学的学科内容和教学要求。
1.2结构力学计算简图及简化要点。
1.3杆件结构的分类。
1.4荷载的分类。
（2）教学要求了解结构力学的任务以及与其它课程的关系，正确理解结构计算简图的概念、简化要点和条件，了解荷载的分类。
2.几何构造分析（6学时）（1）教学内容2.1几何构造分析中的几个基本概念。
2.2平面几何不变体系的组成规律。
2.3平面杆件体系的计算自由度。
（2）教学要求理解几何不变体系、几何可变体系、几何瞬变体系、自由度（静力自由度）约束及其类型等基本概念。
正确理解和应用几何不变体系的组成规则（两刚片法则、三刚片法则、二元体法则），会计算平面杆件体系的计算自由度。
3.静定结构的内力计算（14学时）（1）教学内容3.1梁的内力计算的回顾。
3.2静定多跨梁的组成、计算和内力图的绘制。
3.3静定平面刚架的内力计算和内力图的绘制。
3.4三铰拱的特点和内力计算。
三铰拱的合理拱轴曲线。
3.5静定平面桁架的特点、组成及分类。
用结点及截面法计算桁架的内力，结点法和截面法的联合应用。
3.6静定组合结构的特点、计算和内力图的绘制。
3.7静定结构的一般性质。
（2）教学要求巩固在材料力学中已经建立的截面法的概念与方法，并把它推广应用在结构计算上。
熟练掌握杆件上的荷载与内力的微分关系、增量关系，并用以定性分析内力图的形状。
熟练掌握分段叠加法作弯矩图的方法。
正确、灵活选取和画出隔离体图，熟练掌握应用隔离体图和平衡条件计算结构支反力、内力的方法；熟练掌握静定梁、静定刚架内力计算和内力图的绘制以及静定平面桁架内力的求解方法；掌握静定组合结构、三铰拱的内力计算和内力图的绘制方法；了解静定结构的力学特征。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三、体系的几何组成性质与计算自由度之间的关系
a) W=1>0
b) W=0
c) W=-1<0
(2) W=0时，体系具有成为几何不变体系所必须的最 少约束数目，但体系不一定是几何不变的。 (3) W<0时，体系有多余约束，但体系也不一定是几 何不变的。
All Rights Reserved 重庆大学土木工程学院®
All Rights Reserved 重庆大学土木工程学院®
二、平面体系的计算自由度
1、刚片体系的计算自由度 以刚片为对象，以地基为参照物，其刚片体系的计 算自由度为
W＝3m-(3g+2h+r)
其中：m为个刚片个数；g为单刚结个数，h为单铰结个数，
r为与地基之间加入的支杆数。
All Rights Reserved
重庆大学土木工程学院®
在应用公式时，应注意以下几点：
（1）地基是参照物，不计入m中。 （2）计入m的刚片，其内部应无多余约束。如果遇到内 部有多余约束的刚片，则应把它变成内部无多余约束的 刚片，而把它的附加约束在计算体系的“全部约束数”d 时考虑进去。
图a是内部没有多余约束的 刚片，而图b、c、d则是内 部分别有1、2、3个多余约 a) 束的刚片，它们可以看作 在图a的刚片内部分别附加 了一根链杆或一个铰结或 c) 一个刚结。
All Rights Reserved 重庆大学土木工程学院®
b)
d)
在应用公式时，应注意以下几点：
(3)刚片与刚片之间的刚结或铰结数目（复刚结或复 铰结应折算为单刚结或单铰结数目）计入g和h。
(4)刚片与地基之间的固定支座和铰支座不计入g和h， 而应等效代换为三根支杆或两根支杆计入r。
All Rights Reserved
2.3 平面体系的计算自由度
一、体系的实际自由度S与计算自由度W的定义 1、体系的实际自由度S 令体系的实际自由度为S，各对象的自由度总和为a， 必要约束数为c，则
S＝a – c
2、体系的计算自由度W 将上式中的必要约束数c改为全部约束数d，则
W＝a – d
只有当体系的全部约束中没有多余约束时，体系的 计算自由度W才等于实际自由度S。
All Rights Reserved 重庆大学土木工程学院®
2、铰接链杆体系的计算自由度
W=2j-(b+r)
其中：
j为体系的铰结数；
b为链杆数为；
r为支杆数
注意：在计算j时，凡是链杆的端点，都应当算作结点， 而且无论一个铰结点上连接几根链杆，都只以1计入j中； 在计算b和r时，链杆与支杆应当区别开来，因为链杆是 内部约束，而支杆则是外部约束，二者不可混淆。
All Rights Reserved 重庆大学土木工程学院®
【例2-3】试求图2-12所示体系的计算自由度。
1 2 3
4
5
解：在该体系中，4、5两处除应算作结点外，同时还 都是固定铰支座。因此，该体系的铰结数j=5，链杆 数b=4，支杆数r=6。故由公式(2-4)，可得
W = 2j-(b+r) = 2×5-(4+6) = 0
All Rights Reserved 重庆大学土木工程学院®
三、体系的几何组成性质与计算自由度之间的关系 先求出图示各体系的W。
a) W=1>0
b) 0
c) W=-1<0
可看出存在以下三种情况： (1) W>0时，体系缺少必要的约束，具有运动自由度， 为几何可变体系。
All Rights Reserved 重庆大学土木工程学院®
重庆大学土木工程学院®
【例2-1】试求图示体系的计算自由度W。
m1 m4 m7 (3)h m2 m5 (1)h m6 (3)g
(1)h m3 (3)h
m8
(3)r
m9 (3)r
m=9，g=3，h=8, r=6
W = 3m-(3g+2h+r) = 3×9-(3×3+2×8+6) = -4
All Rights Reserved 重庆大学土木工程学院®
【例2-2】试求图2-11所示体系的计算自由度。
m1
(1)g (1)h m2 (2)g m3 (3)r m5 m7 (3)r m4 (1)h (1)g m6 (2)g (1)h m8 m9 (3)r (1)h
m=9，g=6，r=9
W = 3m-(3g+2h+r) = 3×9-(3×6+2×4+9) = -8
三、体系的几何组成性质与计算自由度之间的关系
a) W=1>0 由此可知：
b) W=0
c) W=-1<0
(1) 若W＞0，体系一定是几何可变的。 (2) 若W≤0，只表明具有几何不变的必要条件，但不 是充分条件。因为体系是否几何不变还取决于约束的 布置是否合理。
All Rights Reserved 重庆大学土木工程学院®