匈牙利算法示例ppt

匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。

美国数学家哈罗德·库恩于1955年提出该算法。

此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。

匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

二分图：二分图又称作二部图，是图论中的一种特殊模型。

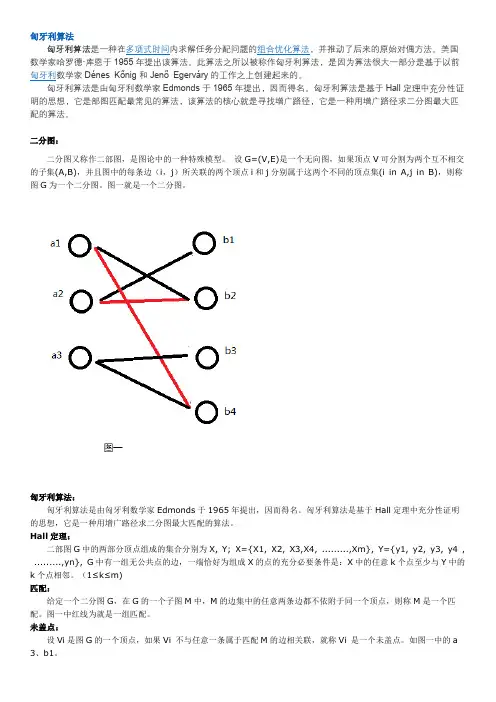
设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

图一就是一个二分图。

匈牙利算法：匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。

匈牙利算法是基于Hall定理中充分性证明的思想，它是一种用增广路径求二分图最大匹配的算法。

Hall定理：二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边，一端恰好为组成X的点的充分必要条件是：X中的任意k个点至少与Y中的k个点相邻。

（1≤k≤m)匹配：给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

图一中红线为就是一组匹配。

未盖点：设Vi是图G的一个顶点，如果Vi 不与任意一条属于匹配M的边相关联，就称Vi 是一个未盖点。

如图一中的a 3、b1。

设P是图G的一条路，如果P的任意两条相邻的边一定是一条属于M而另一条不属于M，就称P是一条交错路。

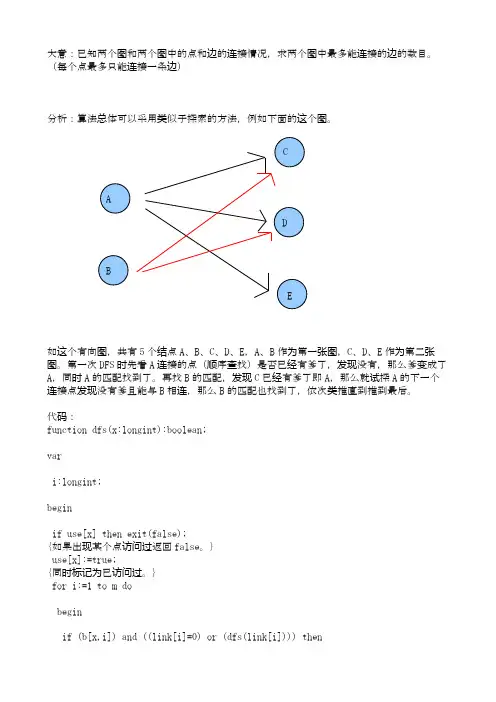
大意：已知两个图和两个图中的点和边的连接情况，求两个图中最多能连接的边的数目。

（每个点最多只能连接一条边）分析：算法总体可以采用类似于探索的方法，例如下面的这个图。

CADBE如这个有向图，共有5个结点A、B、C、D、E，A、B作为第一张图，C、D、E作为第二张图。

第一次DFS时先看A连接的点（顺序查找）是否已经有爹了，发现没有，那么爹变成了A，同时A的匹配找到了。

再找B的匹配，发现C已经有爹了即A，那么就试探A的下一个连接点发现没有爹且能与B相连，那么B的匹配也找到了，依次类推直到推到最后。

代码：function dfs(x:longint):boolean;vari:longint;beginif use[x] then exit(false);{如果出现某个点访问过返回false。

}use[x]:=true;{同时标记为已访问过。

}for i:=1 to m dobeginif (b[x,i]) and ((link[i]=0) or (dfs(link[i]))) then{如果要连的点还没爹可以连，或者是它的爹的所连的点还有剩余就可以继续（前提是必须可以相连）。

}beginlink[i]:=x;{修改爹。

}exit(true);end;end;exit(false);end;procedure XYL;vari:longint;beginfor i:=1 to n do{先进行查找。

}beginfillchar(use,sizeof(use),false);{初始化每个点都未访问过以便遍历图。

}if dfs(i) then inc(ans);{返回true说明可以匹配。

}end;writeln(ans);end;。

匈⽛利算法（⼆分图）---------------------------------------------------------------------题材⼤多来⾃⽹络，本篇由神犇整理基本概念—⼆分图⼆分图：是图论中的⼀种特殊模型。

若能将⽆向图G=(V,E)的顶点V划分为两个交集为空的顶点集，并且任意边的两个端点都分属于两个集合，则称图G为⼀个为⼆分图。

匹配：⼀个匹配即⼀个包含若⼲条边的集合，且其中任意两条边没有公共端点。

如下图，图3的红边即为图2的⼀个匹配。

1 最⼤匹配在G的⼀个⼦图M中，M的边集中的任意两条边都不依附于同⼀个顶点，则称M是⼀个匹配。

选择这样的边数最⼤的⼦集称为图的最⼤匹配问题,最⼤匹配的边数称为最⼤匹配数.如果⼀个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

如果在左右两边加上源汇点后，图G等价于⼀个⽹络流，最⼤匹配问题可以转为最⼤流的问题。

解决此问的匈⽛利算法的本质就是寻找最⼤流的增⼴路径。

上图中的最⼤匹配如下图红边所⽰：2 最优匹配最优匹配⼜称为带权最⼤匹配，是指在带有权值边的⼆分图中，求⼀个匹配使得匹配边上的权值和最⼤。

⼀般X和Y集合顶点个数相同，最优匹配也是⼀个完备匹配，即每个顶点都被匹配。

如果个数不相等，可以通过补点加0边实现转化。

⼀般使⽤KM算法解决该问题。

3 最⼩覆盖⼆分图的最⼩覆盖分为最⼩顶点覆盖和最⼩路径覆盖：①最⼩顶点覆盖是指最少的顶点数使得⼆分图G中的每条边都⾄少与其中⼀个点相关联，⼆分图的最⼩顶点覆盖数=⼆分图的最⼤匹配数；②最⼩路径覆盖也称为最⼩边覆盖，是指⽤尽量少的不相交简单路径覆盖⼆分图中的所有顶点。

⼆分图的最⼩路径覆盖数=|V|-⼆分图的最⼤匹配数；4 最⼤独⽴集最⼤独⽴集是指寻找⼀个点集，使得其中任意两点在图中⽆对应边。

对于⼀般图来说，最⼤独⽴集是⼀个NP完全问题，对于⼆分图来说最⼤独⽴集=|V|-⼆分图的最⼤匹配数。

什么是二分图，什么是二分图的最大匹配，二分图的最大匹配有两种求法，第一种是最大流（我在此假设读者已有网络流的知识）；第二种就是我现在要讲的匈牙利算法。

这个算法说白了就是最大流的算法，但是它跟据二分图匹配这个问题的特点，把最大流算法做了简化，提高了效率。

匈牙利算法其实很简单，但是网上搜不到什么说得清楚的文章。

所以我决定要写一下。

最大流算法的核心问题就是找增广路径（augment path）。

匈牙利算法也不例外，它的基本模式就是：初始时最大匹配为空while 找得到增广路径do 把增广路径加入到最大匹配中去可见和最大流算法是一样的。

但是这里的增广路径就有它一定的特殊性，下面我来分析一下。

（注：匈牙利算法虽然根本上是最大流算法，但是它不需要建网络模型，所以图中不再需要源点和汇点，仅仅是一个二分图。

每条边也不需要有方向。

）图1是我给出的二分图中的一个匹配：［1，5］和［2，6］。

图2就是在这个匹配的基础上找到的一条增广路径：3->6->2->5->1->4。

我们借由它来描述一下二分图中的增广路径的性质：(1)有奇数条边。

(2)起点在二分图的左半边，终点在右半边。

(3)路径上的点一定是一个在左半边，一个在右半边，交替出现。

（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连，不要忘记哦。

）(4)整条路径上没有重复的点。

(5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。

（如图1、图2所示，［1，5］和［2，6］在图1中是两对已经配好对的点；而起点3和终点4目前还没有与其它点配对。

）(6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。

（如图1、图2所示，原有的匹配是［1，5］和［2，6］，这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。

而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。

）(7)最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。

数学建模匈牙利算法
（实用版）
目录
一、匈牙利算法简介
二、匈牙利算法的基本原理
三、匈牙利算法的应用实例
四、匈牙利算法的优点与局限性
正文
一、匈牙利算法简介
匈牙利算法（Hungarian algorithm）是一种求解二分图最大匹配问题的经典算法，由匈牙利数学家 Mátyás Klán 首先提出。

该算法主要用于解决一些实际问题，如任务分配、资源调度等，其核心思想是尽可能地将两个顶点之间的距离缩小，从而实现图的最大匹配。

二、匈牙利算法的基本原理
1.匈牙利算法的基本思想是“贪心”，即每一步都选择当前可以得到的最佳匹配。

2.从未匹配的顶点中选择距离最小的两个顶点进行匹配，直到所有顶点都匹配完毕或者再也找不到匹配的顶点为止。

3.如果当前未匹配的顶点数量为奇数，则无法进行匹配，算法结束。

三、匈牙利算法的应用实例
1.任务分配：假设有 n 个任务和 n 个工人，每个工人完成不同任务的效率不同，匈牙利算法可以帮助我们找到最优的任务分配方案，使得总效率最大。

2.资源调度：假设有 m 个资源和 n 个任务，每个任务需要不同数量
的资源，匈牙利算法可以帮助我们找到最优的资源调度方案，使得总资源消耗最小。

四、匈牙利算法的优点与局限性
1.优点：匈牙利算法思路简单，计算效率较高，可以解决实际生活中的许多问题。

2.局限性：匈牙利算法只能解决无向图的最大匹配问题，对于有向图和带权图，需要进行相应的改进。

最大匹配之匈牙利算法模板。

要学习匈牙利算法先要懂得二部图的各种概念。

下面给出由o( _ )o MiYu 总结的普通性概念，这些概念很重要，一定要懂。

二分图的基本概念: ( 意思就是全部的点分成了2个集合 x, y. 每个集合中的顶点互相间没有边 ) 一个无向图 G = V, E , 假如存在两个集合X, Y, 使得X Y=V, X Y= , 并且每一条边e={x, y} 有x X,y Y, 则称G为一个二分图(bipartite graph). 常用来表示一个二分图. 若对X中任一x 及Y中任一y 恰有一边e E, 使e = {x, y}, 则称G为彻低二分图(complete bipartite graph). 二分图的性质： ( 交叉轨和增广路的概念很重要 ) 定理：无向图G为二分图的充分须要条件是，G起码有两个顶点,且其全部回路的长度均为偶数. 匹配：设G=为二分图，假如M&be;E，并且M中没有任何两边有公共端点。

M= 时称M为空匹配. 盖点: 若M是二分图的一个匹配, 将M中的边多所关联的顶点称为盖点, 其余则为未盖点. 交叉轨: 若一条路径上属于M的边和不属于M 的边交替浮现, 则称该路径为交叉轨. 增广路径: 若路径 P 是一条起始点和尽头都是未盖点的交叉轨, 那么 P 称为 M 的增广路径. 最大匹配: G的全部匹配中边数最多的匹配称为最大匹配. 性质1 : 一条关于M的增广路径的长度必为奇数, 且路上的第一条边和最后一条边都不属于M.性质2 : 对于一条关于M的增广路径 P, 将M 中属于P的边删去, 将P中不属于M 的边添加到M中,所得到的边集合计为 M P, 则 M P 比 M 多一条匹配边.性质3 : M 为 G 的一个最大匹配当且仅当不存在关于M的增广路径.hall 定理 : 对于二分图 G = ( X, Y, E ) , 存在一个匹配M, 使得 X 的全部顶点关于M饱和的充要条件是: 对 X 的任一子集A , 对A邻接的点集为P (A), 恒有 : | P[A] | = | A |其中性质 2 和性质 3 和 hall 定理的充分性证实就是匈牙利算法的基础 .. 二分图的最小顶点笼罩 ==== 最大匹配 DAG图的最小路径笼罩数 == 节点数最大匹配数二分图的最大自立集数 = 节点数最大匹配数在二分图中求最少的点，让每条边都起码和其中的一第1页共2页。