二分图相关问题

5经典图论问题5.1 一笔画问题一笔画算法即是从起点a开始选择关联边（第一这条边不是往回倒，第二这条边在前面延伸路上没有出现过）向前延伸，如果到达终点b，得到a—b迹，判断路上的的边数是否为图的总边数，是就终止，否则选择迹上某个关联边没有用完的顶点v，用同样方式再搜索v—v的闭迹，添加到a—b迹上，即得到a—v---v—b迹，如果这个迹的边数还没有达到总边数，则再选择迹上某个关联边没有用完的顶点。

逐步扩展即可。

二、弗罗莱（Fleury ）算法任取v 0∈V(G)，令P 0=v 0；设P i =v 0e 1v 1e 2…e i v i 已经行遍，按下面方法从中选取e i+1： （a ）e i+1与v i 相关联；（b ）除非无别的边可供行遍，否则e i+1不应该为G i =G-{e 1,e 2, …, e i }中的桥（所谓桥是一条删除后使连通图不再连通的边）；（c ）当（b ）不能再进行时，算法停止。

5.2 中国邮递员问题（CPP ）规划模型：设ij x 为经过边j i v v 的次数，则得如下模型。

∑∈=Ev v ij ijji x z ϖmin∑∑E∈E∈∈=j i i k v v i v v ki ij V v x x ,E ∈∈≤j i ij v v N x ,1..t s5.3旅行推销员问题（TSP，货郎担问题）（NPC问题）定义：包含图G的所有定点的路（圈）称为哈密顿路（圈），含有哈密顿圈得图称为哈密顿图。

分析：从一个哈密顿圈出发，算法一：（哈密顿圈的充要条件：一包含所有顶点的连通子图，二每个顶点度数为2）象求最小生成树一样，从最小权边加边，顶点度数大于3以及形成小回路的边去掉。

算法二：算法三：示例：设旅行推销员的矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛01086100111281101565150规划模型：先将一般加权连通图转化成一个等价的加权完全图，设当从i v 到j v 时，1=ij x ，否则，0=ij x ，则得如下模型。

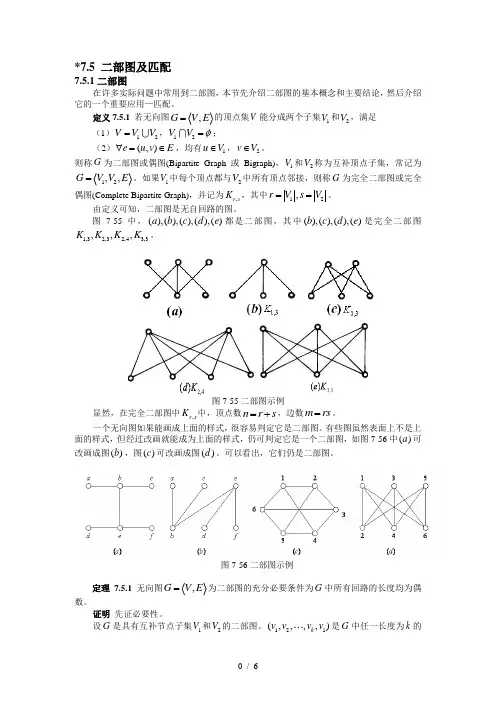
*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图，本节先介绍二部图的基本概念和主要结论，然后介绍它的一个重要应用—匹配。

定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ，满足（1）12V V V =，12V V φ=；（2）(,)e u v E ∀=∈，均有1u V ∈，2v V ∈。

则称G 为二部图或偶图(Bipartite Graph 或Bigraph)，1V 和2V 称为互补顶点子集，常记为12,,G V V E =。

如果1V 中每个顶点都与2V 中所有顶点邻接，则称G 为完全二部图或完全偶图(Complete Bipartite Graph)，并记为,r s K ，其中12,r V s V ==。

由定义可知，二部图是无自回路的图。

图7-55中，(),(),(),(),()a b c d e 都是二部图，其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。

图7-55二部图示例显然，在完全二部图中,r s K 中，顶点数n r s =+，边数m rs =。

一个无向图如果能画成上面的样式，很容易判定它是二部图。

有些图虽然表面上不是上面的样式，但经过改画就能成为上面的样式，仍可判定它是一个二部图，如图7-56中()a 可改画成图()b ，图()c 可改画成图()d 。

可以看出，它们仍是二部图。

图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。

证明 先证必要性。

设G 是具有互补节点子集1V 和2V 的二部图。

121(,,,,)k v v v v 是G 中任一长度为k 的回路，不妨设11v V ∈，则211m v V +∈，22m v V ∈，所以k 必为偶数，不然，不存在边1(,)k v v 。

再证充分性。

设G 是连通图，否则对G 的每个连通分支进行证明。

1、读“地球公转示意图”，回答下列问题：（1）、地球围绕着 的旋转运动叫公转运动；公转周期是__ ____；公转方向是。

并在图乙中的公转轨道上，用箭头画出公转方向。

（2）、图甲中，A 点坐标（ ， ），位于 半球（东/西），位于 半球（南/北），位于 纬度（高/中/低）；B 点坐标（ ， ），位于五带中的 带。

（3）、在A 、B 两点中，先看到日出的是 点（A/B ），先看到日落的是 点（A/B ）。

（4）、A 点位于B 点的 方向，B 点位于A 点的 方向。

（5）、图乙中，①节气 ，日期 ；②节气 ，日期 ；③节气 ，日期 ；④节气 ，日期 。

（6）、考查直射点：①直射点 ，②直射点 ，③直射点 ，④直射点 。

（7）、考查直射点变化：观察图乙和图丙，图乙中地球由②到③属于图丙中的 段（a/b/c/d ），③到④是 段（a/b/c/d ），④到①是 段（a/b/c/d ），①到②是 段（a/b/c/d ）。

（8）、考查北半球获得热量：②这一天，北半球获得太阳光热量最___ ___（多或少或一样多），④这一天，北半球获得太阳光热量最___ ___（多或少或一样多），③①这一天，北半球获得太阳光热量最___ ___（多或少或一样多）。

（9）、考查昼夜长短情况：（北半球）②这一天昼夜情况 ，④昼夜情况 ，①昼夜情况 ，③昼夜情况 。

（10）、考查昼夜长短变化：在图丙a 、b 、c 、d 四段中，昼变短，夜变长的是 ，昼变长，夜变短的是 ；昼长夜短的是 ，昼短夜长的是 。

（11）、灵活运用：国庆节的时候，昼夜情况是 ，太阳直射点在图丙中a 、b 、c 、d 段的_____段。

（12）、当太阳直射点处在图2中的a 段时，此时段北极圈内极昼范围的变化趋势是（ ）A ．全部到无B ．无到全部C ．一半到全部D ．全部到一半2、读下图，回答下列问题：（1）、在北极附近的弧线和赤道上补绘箭头，以正确表示地球自转的方向。

⼆分图概念及性质 段段续续的看⼆分图已经有些时⽇了。

现在借着周末整理⼀下这么多天对⼆分图的掌握程度。

也好对⼆分图有个整体的认知。

另外，此⽂只针对与⼆分图的⼀些概念和性质，不涉及求最⼤匹配的算法。

好吧，切⼊正题： ⾸先我们抛开⼆分图严谨准确的定义，从⼀个感性的⾓度来认识⼀下什么是⼆分图。

所谓⼆分图，就是能够把图中的定点分成两个X，Y两部分；并且整个图的边只存在于X与Y之间。

就是说，X与Y的内部是不存在边的，否则的话就不是⼆分图了。

举个例⼦：如果把整个⼈类中的男⼈和⼥⼈看成顶点，⼈与⼈之间的恋爱关系（这⾥只讨论异性之间的正常恋爱，同性恋是不被承认的）为边来建⽴图模型的话。

那么这其实就是⼀个⼆分图，其中的男⼈为X部分，⼥⼈为Y部分。

好了，现在我们给出⼆分图严谨的科学定义： 假设图G=（V，E）是⼀个⽆向图，若顶点集 V 可以分解成两个互不相交的⼦集（A，B），并且图中的所有边（i，j）的端点 i，j 分别属于⼦集 A，B 中的元素，则称图 G 是⼀个⼆分图。

为了更好的叙述下⽂，先让我们清楚⼀个概念： 匹配：⽆公共点的边集合。

（形象点就是 X与Y之间的边的个数） 匹配数：边集中边的个数。

最⼤匹配：匹配数最⼤的匹配。

边独⽴集：指图中边集的⼀个⼦集，且该⼦集中的任意两条边之间没有公共点。

（对⽐匹配的概念我们发现，其实边独⽴集和匹配是⼀个概念） 最⼤边独⽴集：包含边数最多的边独⽴集。

（其实就是最⼤匹配，为了⽅便，以后统称最⼤匹配）图1如图1，如果<1,4>是⼀个合法匹配，那么<1,5>就不是⼀个合法的匹配，因为它们有公共点1 。

同样的如果<2,5>是⼀个合法的匹配，那么<2,6>和<3,5>就不是⼀个合法的匹配。

不难看出，其中最⼤匹配是边集：{1， 4， 5}，最⼤匹配数为3 。

独⽴集： 是指图的顶点集的⼀个⼦集，且该⼦集中的任意两个顶点之间不存在边。

二分图的定义二分图的定义非常简单，有两组顶点，一组顶点记为L ，另一组记为R ，L 和R 没有公共的元素，并且所有的边都是连接L 和R 中的点的，对于L 和R 本身，它们内部的任何两个点都没有边相连，这样的无向图就叫二分图。

《组合数学》上这样讲解：二分图可描述为：一，顶点的集合；二，将该顶点集分成两部分的一个划分；三，连接一部分的一个顶点与另一部分的一个顶点的边的集合。

二分图是无向图，那么什么样的无向图是二分图呢？有以下定理：定理：无向图G 为二分图的充分必要条件是，G 至少有两个顶点, 且其所有回路的长度均为偶数。

证明：至少两个顶点，这个显然，把这个条件忽略掉，着重考虑回路长度为偶数这一条件。

先证充分性：由于图中可能有回路也可能无回路，无回路的情况应该最简单，自然考虑分类讨论。

于是，分类讨论后，充分性的证明转化成以下两个命题：a)所有无回路的无向图都是二分图；b)所有有回路且回路长度为偶数的无向图都是二分图。

对于a) ，因为无回路无向图总是能把它画成一棵树，所以，这个命题等价于：所有的树都是二分图。

到这里，命题a) 证明显然，因为有一种很简单的从树构造二分图的方法：令树的奇数层的结点为集合L ，令树的偶数层结点为集合R ，这样就从树得到了一个二分图。

再看命题b) ，可以把b) 转化为a) 。

对于图中的每一个回路，我们都从中拿掉一条边，这样可以消灭所有的回路，由a) 知消灭掉所有回路之后的图是二分图。

把此时得到的二分图画成一棵树，拿掉一条边后的回路此时就是树中的一条路径，并且路径的长度为奇数，这就意味着路径的头结点和尾结点所在层数的编号一个是奇数一个是偶数，用上面的从树构造二分图的方法知，头结点和尾结点分别在集合L 中和集合R 中，我们再把拿掉的这条边加上去，只不过是在L 和R 中的两个顶点间连接了一条边，图仍然是原来的二分图。

至此，充分性得证。

再证必要性。

假设二分图中的一条回路是(v0, v1, v2, …, vm, v0) ，由于是二分图，相邻顶点必不属于同一个集合，用L 标记属于集合L 的点，用R 标记属于集合R 的点，不妨假设v0 属于L ，则上面的回路可以标记为L, R, L, R, …, L, R ，由此可见，回路必有偶数个顶点，因此必有偶数条边。

二分图匹配一、二分图的概念二分图又称作二部图，是图论中的一种特殊模型。

设G=(V,{R})是一个无向图。

如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。

则称图G为二分图。

二、最大匹配给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

三、匈牙利算法求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。

但是这个算法的复杂度为边数的指数级函数。

因此，需要寻求一种更加高效的算法。

1、增广路的定义(也称增广轨或交错轨)：若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

由增广路的定义可以推出下述三个结论：●P的路径长度必定为奇数，第一条边和最后一条边都不属于M。

●P经过取反操作可以得到一个更大的匹配M’。

●M为G的最大匹配当且仅当不存在相对于M的增广路径。

2、用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出)。

算法轮廓：(1)置M为空(2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替M(3)重复(2)操作直到找不出增广路径为止程序清单：Function find(k:integer):integer;var st,sf,i,j,t:integer;queue,father:array[1..100] of integer;beginqueue[1] := k; st := 1; sf := 1;fillchar(father,sizeof(father),0);repeatfor i:=1 to n doif (father[i]=0)and(a[queue[st],i]=1) thenbeginif match2[i]<>0 thenbegininc(sf);queue[sf] := match2[i];father[i] := queue[st];end elsebeginj := queue[st];while true dobegint := match1[j];match1[j] := i;match2[i] := j;if t = 0 then break;i := t; j := father[t];end;find := 1;exit;end;end;inc(st);until st>sf;find := 0;end;在主程序中调用下面的程序即可得出最大匹配数。

⼆分图问题⼀、问题描述 给定⼀个具有n个顶点的图，要给图上每个顶点染⾊并且要使相邻的顶点的颜⾊不同，问是否最多⽤2种颜⾊进⾏染⾊？没有重边和⾃环。

把相邻顶点染成不同颜⾊的问题叫做图的着⾊问题。

对图进⾏染⾊所需的最⼩颜⾊数，称为最⼩着⾊数。

最⼩着⾊数为2的图称为⼆分图，如下图所⽰就是⼀个⼆分图。

下⾯代码是⽤来判断是否⼆分图。

⼆、思路 直接DFS即可，要注意代码⾥⾯的⼀些细节。

三、代码1public class图的着⾊_⼆分图 {2static boolean dfs(MyNode node, int c) {3 node.color = c;// 同时标记已访问和具体颜⾊4for (int i = 0; i < node.size(); i++) {// 遍历所有neighbor5 MyNode neighbor = (MyNode) node.getNeighbor(i);// 具体的neighbor6// 如果相邻节点颜⾊⼀样，返回false7if (neighbor.color == c)8return false;9// 没有被染⾊，就染不同颜⾊进⾏递归10if (neighbor.color == 0) {11boolean res = dfs(neighbor, -c);12if (!res)13return false;14 }15 }16return true;17 }1819public static void main(String[] args) {20// 下⾯的数据表⽰的就是上⾯的图21 MyNode n1 = new MyNode(1);22 MyNode n2 = new MyNode(2);23 MyNode n3 = new MyNode(3);24 MyNode n4 = new MyNode(4);2526 n1.add(n2);27 n1.add(n4);2829 n2.add(n1);30 n2.add(n3);3132 n3.add(n2);33 n3.add(n4);3435 n4.add(n1);36 n4.add(n3);3738// 任意顶点都可以39 System.out.println(dfs(n1, 1)); // 输出 true40 }4142// GraphNode_AL这个类在前⾯博客邻接表表⽰图43static class MyNode extends GraphNode_AL {44int color;4546public MyNode(int val) {47super(val);48 }4950public MyNode(int val, int color) {51super(val);52this.color = color;53 }54 }55 }。

算法———艺术二分图匹配剖析很多人说，算法是一种艺术。

但是对于初学者的我，对算法认识不是很深刻，但偶尔也能感受到他强大的魅力与活力。

这让我追求算法的脚步不能停止。

下面我通过分析匈牙利算法以及常用建图方式，与大家一起欣赏算法的美。

匈牙利算法匈牙利算法是用来解决最大二分图匹配问题的，所谓二分图即“一组点集可以分为两部分，且每部分内各点互不相连，两部分的点之间可以有边”。

所谓最大二分图匹配即”对于二分图的所有边，寻找一个子集，这个子集满足两个条件，1：任意两条边都不依赖于同一个点。

2：让这个子集里的边在满足条件一的情况下尽量多。

首先可以想到的是，我们可以通过搜索，找出所有的这样的满足上面条件的边集，然后从所有的边集中选出边数最多的那个集合，但是我们可以感觉到这个算法的时间复杂度是边数的指数级函数，因此我们有必要寻找更加高效的方法。

目前比较有效的方法有匈牙利算法和通过添加汇点和源点的网络流算法，对于点的个数都在200 到300 之间的数据，我们是采取匈牙利算法的，因为匈牙利算法实现起来要比网络流简单些。

下面具体说说匈牙利算法：介绍匈牙利之前，先说说“增广轨”。

定义：若P是图G中一条连通两个未匹配顶点的路径，并且属最大匹配边集M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广轨定义总是抽象的下面通过图来理解它。

图中的线段（2->3, 3->1, 1->4）便是上面所说的p路径，我们假定边（1,3）是以匹配的边，（2,3）（1,4）是未匹配的边，则边（4,1）边（1,3）和边（3,2）在路径p上交替的出现啦，那么p就是相对于M的一条增广轨，这样我们就可以用边1,4 和边2,3来替换边1,3 那么以匹配的边集数量就可以加1,。

匈牙利算法就是同过不断的寻找增广轨实现的。

很明显如果二分图的两部分点分别为n 和m，那么最大匹配的数目应该小于等于MIN（n,m）; 因此我们可以枚举任第一部分（的二部分也可以）里的每一个点，我们从每个点出发寻找增广轨，最后吧第一部分的点找完以后，就找到了最大匹配的数目，当然我们也可以通过记录找出这些边。

在离散数学中，图论是一门重要的理论基础课程，它研究的是由节点和边构成的图结构。

图的匹配和二分图是图论中的两个重要概念，它们在现实生活中有着广泛的应用。

首先，我们来介绍一下图的匹配。

图的匹配指的是在一个图中选取一些边，使得这些边彼此不相交，即任意两条边不共享同一个顶点。

图的匹配问题可以用最优化问题来描述，既需要满足匹配条件，还需要满足某种优化目标。

例如，在一个社交网络图中，选择一些用户与其他用户进行配对，使得两个不认识的用户不会被配对在一起，同时目标是使得配对用户的兴趣爱好相似度最大化。

在这个问题中，边表示用户之间是否认识，而边的权值表示兴趣爱好的相似度。

其次，我们来介绍一下二分图。

二分图是一种特殊的图结构，它可以被划分为两个独立的顶点集合，使得同一个顶点集合内的顶点之间没有边相连。

换句话说，二分图中不存在奇圈。

二分图的一个典型例子是婚姻匹配问题。

假设有n个男性和n个女性，他们之间有多种可能的配对方式，但是每个人只能与另一个不同性别的人结婚。

这时，我们可以用一个二分图来表示这个问题，其中男性和女性分别作为两个顶点集合，边表示可能的配对。

然后，我们可以使用图的匹配算法来找到一个最佳匹配方案。

图的匹配和二分图在离散数学中有着重要的研究价值和应用价值。

首先，图的匹配可以用于解决资源分配问题。

例如，在一个工厂中，有m个任务需要分配给n个员工进行处理，每个员工对某些任务有一定的能力要求，而每个任务也需要一定的时间完成。

这时，我们可以将员工和任务分别作为两个顶点集合，边的权值表示员工对任务的能力是否满足要求和任务完成时间。

然后，我们可以使用图的匹配算法来找到一个最佳的任务分配方案，使得员工的工作量最小。

其次，二分图可以用于解决社交网络分析问题。

如今，社交网络已经成为人们日常生活中重要的一部分，人们之间通过社交网络平台进行交流和连接。

我们可以使用二分图来表示社交网络的结构，其中一个顶点集合表示用户，另一个顶点集合表示用户之间的好友关系，边的权值表示用户之间的相似性度量。

【算法】⼆分图的判定⼆分图的判定 给定⼀个具有n个顶点的图。

要给图上每个顶点染⾊，并且要使相邻的顶点颜⾊不同。

判断是否能最多⽤两种颜⾊进⾏染⾊。

题⽬保证没有重边和⾃环。

概念：把相邻顶点染成不同颜⾊的问题叫做图的着⾊问题。

对图进⾏染⾊所需要的最⼩颜⾊数称为最⼩着⾊度。

最⼩着⾊度为2的图称作⼆分图。

分析：如果只⽤两种颜⾊，那么确定⼀个顶点的颜⾊之后，和它相邻的顶点的颜⾊也就确定了。

因此，选择任意⼀个顶点出发，依次确定相邻顶点的颜⾊，就可以判断是否可以被2种颜⾊染⾊了。

这个问题⽤深度优先搜索可以简单实现。

#include <bits\stdc++.h>using namespace std;#define MAX_V 1000//输⼊vector<int> G[MAX_V]; //图int V; //顶点数int color[MAX_V]; //顶点的颜⾊（1 or -1）//顶点v，颜⾊cbool dfs(int v,int c){color[v] = c;//把当前顶点相邻的顶点扫⼀遍for(int i = 0;i < G[v].size(); i++){//如果相邻顶点已经被染成同⾊了,说明不是⼆分图if(color[G[v][i]] == c) return false;//如果相邻顶点没有被染⾊,染成-c,看相邻顶点是否满⾜要求if(color[G[v][i]] == 0 && !dfs(G[v][i],-c)) return false;}//如果都没问题，说明当前顶点能访问到的顶点可以形成⼆分图return true;}void solve(){//可能是不连通图，所以每个顶点都要dfs⼀次for(int i = 0;i < V; i++){if(color[i] == 0){//第⼀个点颜⾊为 1if(!dfs(i,1)){cout << "No" << endl;return;}}}}int main(){//输⼊}。

基于二分图完美匹配算法的变换序列问题图论模型起源于“哥尼斯堡的七桥问题”，是指对一些客观事物进行抽象、化简，并用图来描述事物特征及内在联系的过程。

在建立图论模型的过程中，和几何模型、运筹学模型一样，也需要用到集合、映射、函数等基本的数学概念和工具。

如何建立问题的图论模型并没有通用的准则。

在复杂的实际问题中，有时我们会感到难以建立适当的模型，这些都需要我们有丰富的经验，灵活的思维以及良好的创造力。

一、变换序列问题描述对于0，1，…，n-1的n个整数，给定一个距离序列d0，d1，…，dn-1，定义一个变换序列t0，t1，…，tn-1使得每个i，ti的环上距离等于di 。

一个合法的变换序列应是0，1，…，n-1的一个排列，任务是要求出字典序最小的那个变换序列。

二、图论模型建立问题抽象成图论模型：建立一个二分图，x集合每个顶点代表0，1，…，n-1的n个整数，y集合每个顶点为对应的n个整数。

x集合的第i个顶点向其环上距离为di的y集合中的两个顶点连一条边。

三、图的有关理论二分图：设x，y都是非空有限顶点集，且x∩y = ，称g=（x，y，e）为二分图。

正则图：定义2若二分图g=（x，y，e）的每一个顶点的都与k条边相连，则称g为k阶正则图。

匹配：图g（v，e）中若干互不相邻的边组成的集合称为图g的一个匹配。

最大匹配：给定一个二分图g（v，e），在g的一个子图m中，m 的边集中的任意两条边都不依附于同一个顶点，则称m是一个匹配。

选择这样的边数最大的子集称为图的最大匹配问题。

完全匹配（或称完备匹配）：如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

完美匹配：若一个匹配既是一个二分图g=（x，y，e）中x到y 的完全匹配，又是y到x的完全匹配，则称这个匹配是二分图g=（x，y，e）的完美匹配。

（此时|x|=|y|）增广路的定义（也称增广轨或交错轨）：若p是图g中一条连通两个未匹配顶点的路径，并且属m的边和不属m的边（即已匹配和待匹配的边）在p上交替出现，则称p为相对于m的一条增广路径。

第九章二分图中的匹配三个典型问题：（1）在一个有禁止位置的m×n棋盘上，能放置非攻击型车的最多个数是多少？（2）在一个有禁止位置的m×n棋盘上，能放置多米诺牌覆盖的最多个数是多少？（3）一个公司有n个工作空缺，需要有一定技能的人填补，同时有m个人申请这些项工作，每人能胜任n项工作中的若干项，问最多有多少项工作能找到合适的人选？9.1 一般的问题描述定义1：令X={x1, x2, …,x m}, Y={y1,y2, …,y n},且X∩Y＝Ф，而△是序偶e=(x,y)的集合，其中x ∈X,y∈Y,那么三元组G＝（X，△，Y）称作二分图。

定义2：令G＝（X，△，Y）是一个二分图，边集△的子集M，若M中没有两条边存在公共点，称M是二分图G的一个匹配。

定义3：设G是一个二分图，定义ρ（G）＝{∣M∣:M是G的一个匹配}为二分图G的最大匹配边数。

9.2 匹配定义1：G＝（X，△，Y），X={x1, x2, …,x m}, Y={y1,y2, …,y n}，满足∣M*∣=ρ（G）的匹配M*称为二分图G的最大匹配。

一般M*不唯一，且∣M*∣=ρ（G）≤min{m,n}。

寻找M*的困难点：（1）若已知ρ（G），那么遍历所有可能的匹配会找到M*，但搜索量巨大；（2）一般ρ（G）并不事先知道，要找到M*，并求出ρ（G）＝∣M*∣难度更大。

定义2：令u和v是二分图G＝（X，△，Y）的任意两个顶点，连接u和v的互异顶点序列：γ：u=u0, u1, u2, …, u p-1, u p=v使得任意两个相邻顶点有一条边连接，即：{ u0, u1},{ u1, u2},…, { u p-1, u p}∈△,那么称序列γ为二分图G的一个链。

链长等于序列的边数p，若u=v, 链γ也叫圈。

定义3：令M为二分图G＝（X，△，Y）中的一个匹配，令M是M的补集，即G的不属于M的边集合，M∪M＝△。

令u和v是顶点，且u和v一个是左顶点（即属于X），一个是右顶点（即属于Y），若连接u和v的链满足下列性质：（1）γ的第一、三、五、、、边属于M；（2）γ的第二、四、六、、、边属于M；（3）u和v都不与M的边相连。

浅析二分图匹配在信息学竞赛中的应用湖南省长沙市长郡中学王俊[摘要]本文通过对几道信息学竞赛题目的分析，举例说明了二分图匹配在信息学竞赛中的应用。

二分图匹配的应用一般是通过分析某些最优化问题的性质，构造出二分图，再通过求得该二分图的最大匹配，最佳匹配等各种形式的匹配从而解决原问题。

[关键字]匹配二分图最小权最大权优化[正文]一引言二分图匹配是信息学竞赛中一类经典的图论算法，在近年来信息学竞赛中有广泛应用。

如果可以以某一种方式将题目中的对象分成两个互补的集合，而需要求得它们之间满足某种条件的一一对应的关系时，往往可以抽象出对象以及对象之间的关系构造二分图，然后利用匹配算法来解决。

这类题目通常需要考察选手对原题进行建模，构造二分图，设计匹配算法，并对其算法进行适当优化等多方面能力。

下面就通过两道例题来说明二分图匹配在信息学竞赛中的一些应用。

二Railway Communication12.1 问题描述某国有n个城镇，m条单向铁路。

每条铁路都连接着两个不同的城镇，且该铁路系统中不存在环。

现需要确定一些列车运行线，使其满足：I)每条铁路最多属于一条列车运行线；II)每个城镇最多被一条列车运行线通过（通过包括作为起点或终点）；III)每个城镇至少被一条列车运行线通过；IV)列车运行线的数量应尽量小。

V)在满足以上条件下列车运行线的长度和应该尽量小。

1Saratov State University 252. Railway Communication2.2 问题分析题目要求列车运行线数最少，又要求在此条件下列车运行线的长度和最小，不便于一起考虑，我们不妨分步研究，先考虑列车运行线数最少的子问题。

则该子问题可建立如下数学模型：给定一个有向无环图G 0=(N 0，A 0)，用尽量少的不相交的简单路径覆盖N 0。

我们可以给问题建立一个二分图G =(N ，A )，如图2。

a) 建立两个互补的结点集合X 和Y ，把点i (0i N ∈)拆成X 结点i 和Y 结点i'。