湖南工业大学信号与系统(A卷)答案

微波技术与天线A 卷一、填空（102⨯）1、充有25.2r =ε介质的无耗同轴传输线，其内、外导体直径分别为mm b mm a 72,22==，传输线上的特性阻抗Ω=__________0Z 。

（同轴线的单位分布电容和单位分布电感分别()()70120104,F 1085.8,ln 2ln 2--⨯==⨯===πμμεπμπεm a b L abC 和m H )2、 匹配负载中的吸收片平行地放置在波导中电场最___________处，在电场作用下吸收片强烈吸收微波能量，使其反射变小。

3、平行z 轴放置的电基本振子远场区只有________和________ 两个分量，它们在空间上___________（选填：平行，垂直），在时间上_______________（选填：同相，反相）。

4、已知某天线在E 平面上的方向函数为()⎪⎭⎫ ⎝⎛-=4sin 4sin πθπθF ，其半功率波瓣宽度_________25.0=θ。

5、旋转抛物面天线由两部分组成，___________ 把高频导波能量转变成电磁波能量并投向抛物反射面，而抛物反射面将其投过来的球面波沿抛物面的___________向反射出去，从而获得很强___________。

二、判断（101⨯）1、传输线可分为长线和短线，传输线长度为3cm ，当信号频率为20GHz 时， 该传输线为短线。

（ 错）2、无耗传输线只有终端开路和终端短路两种情况下才能形成纯驻波状态。

（错 ）3、由于沿smith 圆图转一圈对应2λ，4λ变换等效于在图上旋转180°，它也等效于通过圆图的中心求给定阻抗（或导纳）点的镜像，从而得出对 应的导纳（或阻抗）。

（ 对）4、当终端负载阻抗与所接传输线特性阻抗匹配时，则负载能得到信源的最大 功率。

（ 错）5、微带线在任何频率下都传输准TEM 波。

（ 错）6、导行波截止波数的平方即2c k 一定大于或等于零。

（ 错）7、互易的微波网络必具有网络对称性。

一、填空题（1*30=30′）1、移动通信按多址方式可分为（）、（）、（）。

2、移动通信的电波传播方式主要有（）、（）、（）、和（）等。

3、常用的移动通信系统有（）、（）、（）、（）、（）和（）。

4、按照调制方式分，数字调制可分为（）、（）、（）和（）。

5、微分集是一种减少（）的分集方式，可以分为（）、（）、（）、（）、（）和（）。

6、GSM的网络子系统由哪几个部分组成（）、（）、（）、（）、（）和（）。

二、选择题（2*5=10′）1、GSM移动通信网与公共电信网络互联采用的是（）。

A、Um接口规范B、Abis接口规范C、7号信令系统D、CDMA2、（）是蜂窝移动通信网络解决用户增多而被有限频谱制约的重大突破。

A、频率再用B、信道均衡C、使用卷积码D、PSK调制3、QAM调制是（）A、2进制调制B、调频方式C、信源编码D、多进制调制4、蜂窝系统的小区分裂是为了（）。

A、增大频率复用B、增大波分复用C、增大时间复用D、三者都不对5、下列关于GSM中TDMA说法不正确的是（）A、每载波8个时隙信道，每个时隙信道可提供一个数字语音用户B、属于模拟移动系统C、8个用户根据时分特性可以共用一套收发设备D、与FDMA比较，减少了7倍的用户设备，从而降低了成本三、判断题（1*8=8′）1、任何一种通信系统都是围绕着如何完成通信的有效性、可靠性和安全性进行不断的优化（）2、位置管理的作用仅仅是位置登记。

（）3、角度分集是利用传输环境的复杂性，调整天线不同角度的馈源，实现在单个天线上不同角度达到信号样值统计上的不相关性来实现等效空间分集的效果。

（）4、在移动台的SIM卡中，有临时移动用户身份号和个人用户密码。

（）5、QPSK是恒包络调制。

（）6、2ASK、2PSK和2FSK中，2PSK的抗干扰能力最好。

（）7、相对于PSTN，移动通信网是接入网。

（）8、最小频移键控MSK信号，在一个比特区间内，相位线性的增加或减少π/2。

一、已知0()f t 如图所示，()()T m t t m T δδ∞=-∞=-∑，T ＝10，2τ=，1）求0()()*()T f t f t t δ=； 2）并作出()f t 的图形；3）求0()f t 的傅立叶变换，并作出其频谱图；4）求()f t 的傅立叶变换，并作出其频谱图。

（20分）[解]:(1) 令 f 0(t)=ε(t+τ)-ε(t-τ) f(t)=f 0(t)*T δ(t) =∑∞-∞=-m mT t t f)](*)([0δ=)(0mT t m f-∑∞-∞=(2)(3) F(j ω)=dt et tj fω-∞∞-⎰)(0=⎰--ττωetj dt=ωj -1[ej ωτ--ej ωτ]=2τs a (ωτ) 其频谱图形为抽样函数频谱(4) 依傅氏变换定义 F n =T1⎰-Ω-22)(TT tjn et f dt=⎰-Ω-ττetjn T1dt=Ω-Ω-jn T etjn 1│ττ-=ΩΩn n Tτsin 20()f ttτ τ- 1=)(2ττΩn T s a其中 n=0,∙∙∙±±,2,1 其频谱图为每隔一个T 位置重复一个笫(3)小题的抽样函数频谱二、 已知连续系统如图1）写出系统的微分方程； 2）求系统的单位冲激响应； 3）画出相应的s 域系统框图；4）求系统函数()H s ；5） 已知()()(3)f t t t εε=--，求()f y t 。

（25分）[解]:(1)以左边加法器为参考点有x “（t ）=f(t)-6x ’(t)-5x(t)i.e x “（t ）+6x ’(t)+5x(t)=f(t) ①以右边加法器为参考点有y(t)=-x ’(t)+2x(t) ② 由式②取 5y=-(5x ’)+2(5x)6y ’=-(6x ’)’+2(6x)y ”=-(x ’)”+2(x)”∴y ”+6y ’+5y=-(x ”+6x ’+5x)’+2(x ”+6x ’+5x)比较式①有 y ”+6y ’+5y=-f ,+2f ③ (2) 对式③求拉氏变换有(s 2+6s+5)y f (s)=(2-s)f(s)∴ H(s)=56s s 22++-s =143+s -547+s ④ −→←LFh(t)=(43e -t -te 547-)ε(t)(3)对原图作以下改动:f(t) −→−F(S); y(t) −→−Y(S); ⎰−→−S-1⎰⎰-∑∑++--()y t6512()f t(4) 由式④己求得系统函数 H(s)=56s s 22++-s⑸ f(t)=ε(t)-ε(t-3)−→←LSF(S)=S1(1-e -3s )Y f (S)=H(S)F(S)=56s s 22++-s S1(1-e -3s) =)1)(5(2++-s s s s(1-e -3s )=(s 52-143+s +5207+s ) (1-e -3s)−→←LSy f (t)=(52-43e -t +207e -5t ) [ε(t)-ε(t-3)]三、 已知离散系统的差分方程为()(1)2(2)()y k y k y k f k ----=1）求系统的单位序列响应()h k ； 2）求()()(3)f k k k εε=--时的()f y k ； 3）求系统函数()H z ；（15分） [解]:(1) 原方程的零状态响应方程为y f (k)-y f (k-1)-2y f (k-2)=f(k)求Z 变换后有Y f (Z)-Z -1Y f (Z)-2Z -2Y f (Z)=F(Z) ∴ (1-Z -1-2Z -2)Y f (Z)=F(Z)∴ H(Z)=21211)()(----=ZZZ F Z Y f =222--Z ZZ ①=ZZ H )(22--Z ZZ =1221++-Z K Z K而 K 1=(Z-2) Z Z H )(│Z=2=32K 2=(Z+1)ZZ H )(│Z=-1=31∴ =ZZ H )(131232++-Z Z 因此, H(Z)= 131232++-Z Z Z Z由H(Z)−→←ZFh(k)有h(k)=)()1(31)(232k k kk εε-+⋅ ② (2) f(k)=)3()(--k k εε−→←ZTF(Z)=(1-Z -3)1-z ZY f (Z)=H(Z) F(Z)=222--Z ZZ (1-Z -3)1-z Z=)1)(2(123----Z Z ZZ=2122--++Z ZZ ZZZ Y f )(=)2(122--++Z ZZ Z Z =12321++-+Z K Z K ZK而 K 1=-21,K 267=,K 3=31∴Z Z Y f )(=-21Z 1+2167-⋅Z +1131+⋅ZY f (Z)=-21+672-⋅Z Z+131+⋅Z Z由Y f (Z))(k y f ZT−→← y f (k)= -)()1(31)()2(67)(21k k k kkεεδ-++(3) 由式①己求出系统函数 H(Z)=222--Z ZZ3已知离散系统的系统函数223()32z z H z z z -=-+，求系统的单位序列响应并写出系统的后向差分方程。

信号与系统考试试题及答案WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】长沙理工大学拟题纸课程编号 1 拟题教研室（或老师）签名 教研室主任签名 符号说明：)sgn(t 为符号函数，)(t δ为单位冲击信号，)(k δ为单位脉冲序列，)(t ε为单位阶跃信号，)(k ε为单位阶跃序列。

一、填空（共30分，每小题3分）1. 已知)()4()(2t t t f ε+=，求_______)("=t f 。

)('4)(2)("t t t f δε+ 2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ，求______)()(=*k h k f 。

}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。

0)(t j Ke j H ωω-=4. 若)(t f 最高角频率为m ω，则对)4(tf 取样的最大间隔是______。

m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。

101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =，试判断该系统是否为线性时不变系统______。

故系统为线性时变系统。

7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ，求该信号的傅立叶变换)(ωj F =______。

故傅立叶变换)(ωj F 不存在。

8. 已知一离散时间系统的系统函数2121)(---+=z z z H ，判断该系统是否稳定______。

故系统不稳定。

9. =+-+⎰∞∞-dt t t t )1()2(2δ______。

310. 已知一信号频谱可写为)(,)()(3ωωωωA eA j F j -=是一实偶函数，试问)(t f 有何种对称性______。

长沙理工大学拟题纸课程编号 1 拟题教研室（或老师）签名 教研室主任签名 符号说明：)sgn(t 为符号函数，)(t δ为单位冲击信号，)(k δ为单位脉冲序列，)(t ε为单位阶跃信号，)(k ε为单位阶跃序列。

一、填空（共30分，每小题3分）1. 已知)()4()(2t t t f ε+=，求_______)("=t f 。

)('4)(2)("t t t f δε+ 2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ，求______)()(=*k h k f 。

}4,6,8,3,4,10,3{)()(-=*k h k f 3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。

0)(t j Ke j H ωω-=4. 若)(t f 最高角频率为m ω，则对)4(t f 取样的最大间隔是______。

m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。

101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =，试判断该系统是否为线性时不变系统______。

故系统为线性时变系统。

7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ，求该信号的傅立叶变换)(ωj F =______。

故傅立叶变换)(ωj F 不存在。

8. 已知一离散时间系统的系统函数2121)(---+=z z z H ，判断该系统是否稳定______。

故系统不稳定。

9. =+-+⎰∞∞-dt t t t )1()2(2δ______。

310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数，试问)(t f 有何种对称性______。

关于t=3的偶对称的实信号。

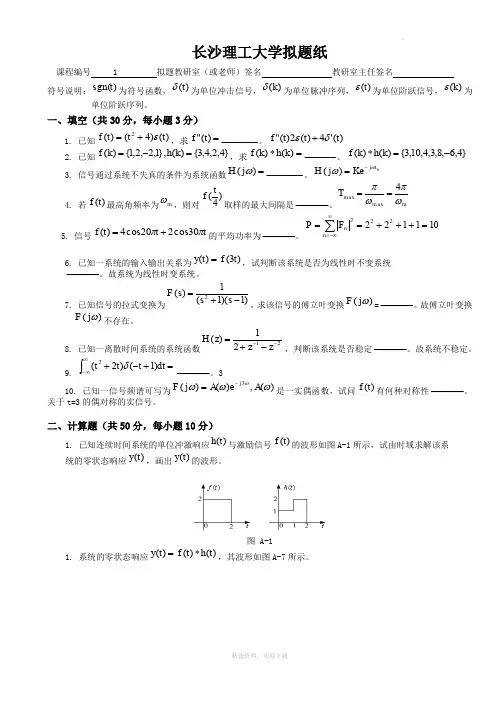
二、计算题（共50分，每小题10分）1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示，试由时域求解该系 统的零状态响应)(t y ，画出)(t y 的波形。

1湖 南 理 工 学 院 成教 期 末 考 试 试 卷课 程 名 称《信号与系统》2010 年度第 I 学期题号 一 二三四五六七八九十总： ：得分数 一、填空题：（ 30 分，每小题 3 分）名份姓 题 1. 已知 f(t)的傅里叶变换为 F(j ω), 则 f(2t-3)的傅里叶变换为生 印学2、e2 tt1 dt。

）（ 3( 2cos 5t ) (t ) dt= 。

卷闭、）s 1√ 4. 已知 F ( s)s 2，则 f (0 ); f ()。

（ 5s 6卷1： 开 5. 已知 FT [(t)](，则 FT [t (t )]： )号j式学形生 6.试 已知周期信号 f (t )cos( 2t ) sin( 4t )，其基波频率为学考 ：s 。

师 周期为教题 ） 7.已知 f (k)3 (n 2) 2 (n5) ，其 Z 变换出（C10 ． 如 图 所 示 是 离 散 系 统 的 Z 域 框 图 ， 该 系 统 的 系 统 函 数H(z)= 。

分。

二 ． (15 分 ) 如下方程和非零起始条件表示的 连续时间因果LTI 系统，d 2 y 5 dy 4 y(t ) 2 df 5 f (t) dt 2 dt dt y(0 ) 2, y'(0 ) 5已知输入 f (t ) e 2 t (t ) 时，试用拉普拉斯变换的方法求系统的零状态响应y zs (t ) 和零输入响应 y zi (t ) ， t 0 以及系统的全响应 y(t ), t 0 。

rad/s ；、F (Z)；收敛域为。

理 ） 物 （7 B3s 20 、8.已 知 连 续 系 统 函 数 H (s)， 试 判 断 系 统 的 稳 定322）s4s 3s 1√： （级 A性：。

年 ：业 别z 2： 专 类 9 ． 已 知 离 散 系 统 函 数 H ( z)z2， 试 判 断 系 统 的 稳 定 级 用 卷0.7z 0.1班 适 试性： 。

一、填空题1、求周期2、DTFT ，已知序列的DTFT ，求平移后的DTFT3、信号处理的三个发展表现 P4答：①由简单的运算走向复杂的运算②有低频走向高频③由一维走向多维4、DFT 隐含的一个性质5、已知H （z ）,求)e (H ωj6、延拓满足的条件7、DFT 的频率分布的取决8、因果系统稳定的主要条件答：<∝∑∝∝ｎ＝－｜｜)(h n 且0n 0)(h <≡，n 二、简答题1、系统单位脉冲响应)(3.0)(n u n h n -=,判断因果与稳定性解：∵当n<0时，-n>0;u(-n)=1; ∴是非因果系统因为当n 趋于无穷时，0.3n 趋于0，所以系统是稳定的2、序列想)1(5.0)(-=n u n X n 求其Z 变换及收敛域并画出零极点分布图 解：由Z 变换的定义可知 ⎩⎨⎧≥<=-=1n ,5.01,0)1(5.0)(x n n n u n n ∑∝∝-=--=n n )1(5.0)(n z n u z X =n ∑∝=1n )z21( =n N 11)5.0(lim ∑=-→∝n z N=⎥⎦⎤⎢⎣⎡--→∝-+11n -11-z 5.01)z 5.0(1z 5.0limN =⎪⎪⎩⎪⎪⎨⎧<>==><---5.0|z |,1|5.0|,5.0|z |,1|5.0|,5.0|z |,1|z 5.0|,z 21111-1即无界即不定即z z 在Z 平面是,收敛域|z|>0/53、)1()()(-+=n n u a n X nδ求其N 点的DFT解:利用有限长序列的DFT 的定义 Nnk wn x k X N n ∑-==10)()(,10-≤≤N k )1()()(-+=n n u a n x n δ)()()()()(102102k R e n u a k R en x k x N N n nk N j n N N n nk N j ∑∑-=--=-+=∴ππ =)()()(1022k R en u a k R e n N n nk N j n N k N j ∑-=--+ππ =)(11)(22k R ae a k R e N k N j NN k N j ππ----+=Naw a N k w N--+114、对线性相位的FIR 滤波器,其单位脉冲响应须具备什么条件? 答：⎪⎩⎪⎨⎧≤≤==∂1-N n 0n)-1-h(N h(n)21-N ，三、计算题1、滤波器的差分方程为)1(5)(4)2(2)1(1)(y -++-+-=n x n x n y n y n(1)用典范型结构实现此系统(2)求该系统的幅度响应并画出幅度响应简图2、设计一个三阶巴特沃思数字滤波器抽样频率为k s 2f = Hz 通带边界频率为500Hz ，采用双线性法设计 解：]cs )c s (2)c s (21[1)(,4T )25.022(ctg 2T )2(ctg 2T c 32c ）（Ω+Ω+Ω+====Ωs H a πω 311-211-11-1z 1*2T )1z 1(8)1z 1(81z 1411|)()z (11----+=-++-++-++==--zz z s H H z s a =23-126z -1--+z ）（ 3，给定如下性能指标，试设计一个线性相位FIR 低通滤波器，求出其单位脉冲响应h(n),通带截止频率为：w ρ=0.4π，阻带起始频率为π6.0w st =，阻带衰减不小于40dB 解：首先求解)(h d n ,根据指标要求其边界频率应为πππωωω5.026.04.02p =+=+=st，，由）（απαω-n )]([sin )(h c d -=n n 得=⎪⎪⎩⎪⎪⎨⎧=≠），（），（）（，，απωαπαωn a n -n )]-(n sin[c c 式中，21-N =α。

2020-2021《信号与系统》期末课程考试试卷适用专业： 考试日期：考试所需时间： 满分：100分一、应用冲激信号的抽样特性，求下列表示式的函数值。

（15分）dt t t e dtt t t f t )2()()5)()()10++∞-∞-∞-∞-⎰⎰δδ dt t t t dtt t t f )6()sin ()6)()()20πδδ-+∞-∞-∞-∞⎰⎰ dt t t t e dt t t u t t tj )]()([)7)2()()3000--∞-∞--∞-∞-⎰⎰δδδω dt t t u t t )2()()400--∞-∞⎰δ 二、绘出下列各时间函数的波形图。

（10分）1) t[u(t)-u(t-1)] 4) (t-1)u(t-1) 2) t ·u(t-1) 5) -(t-1)[u(t-1)] 3)t[u(t)-u(t-1)]+u(t-1)三、判断下列系统是否为线性的，时不变的，因果的？（15分）)()()()2)()()1t u t e t r dtt de t r •==)1()()4)()](sin[)()3t e t r t u t e t r -== )()()6)2()()52t e t r t e t r ==ττττd e tt r d e tt r )(5)()8)()()7⎰⎰∞-=∞-= 四、求下列两组卷积（10分）)()()(),1()()()1t f t f t s t u t u t f *=--=求)()()(),2()1()()2t f t f t s t u t u t f *=---=求五、求下列函数的拉氏变换，注意阶跃函数的跳变时间。

（10分）)2()()1-=-t u e t f t )()()2)2(t u e t f t --= )2()()3)2(-=--t u e t f t )1()2sin()()4-=t u t t f)]2()1()[1()()5----=t u t u t t f六、求下列函数的拉普拉斯逆变换。

淮南师范学院201 -201学年第 学期《信号与系统》A 卷参考答案及评分标准一、填空题（每题2分，共10分） 1．离散信号2．()f t 3．冲激信号或()t δ 4．可加性 5．()t δ 二、选择题（每题2分，共10分） 1. (B) 2. (C) 3. (C) 4. (A) 5. (C)三、判断题（每题2分，共10分） 1. × 2. √ 3. √ 4. √ 5. √四、简答题（每题5分，共10分）1. 简述根据数学模型的不同，列出系统常用的几种分类。

（本题5分）答：根据数学模型的不同,系统可分为4种类型. -----------------------(1分) (1) 即时系统与动态系统 -----------------------(1分) (2) 连续系统与离散系统 -----------------------(1分)(3) 线性系统与非线性系统 -----------------------(1分) (4) 时变系统与时不变系统 -----------------------(1分)2. 简述稳定系统的概念及连续时间系统时域稳定的充分必要条件。

（本题5分）答：（1）一个系统（连续的或离散的）如果对任意的有界输入，其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统。

-----------------------(2分)（2）连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰-----------------------(3分)五、计算题（每题10分，共60分） 1、如有两个序列11,0,1,2()0,k k f k +=⎧=⎨⎩ 其余21,0,1,2()0,k f k =⎧=⎨⎩ 其余试求卷积和12()()()f k f k f k =*（本题10分）解： 1 1 1⨯ 1 2 3-------------------------- 3 3 3 2 2 21 1 1---------------------------------1 3 6 5 3 -----------------------(5分){}12()()()0,1,3,6,5,3,00f k f k f k k =*=↑= -----------------------(5分)2、求象函数2()(2)(4)sF s s s =++的拉普拉斯逆变换()f t （本题10分）解：12()24k k F S s s =+++2424s s =-+++ -----------------------(5分) 24()(24)()tt f t ee t ε--∴=-+ -----------------------(5分)3. 已知某LTI 离散系统的差分方程为()(1)2(2)2()y k y k y k f k +---=, 求单位序列响应()h k （本题10分）解：12()()2()2()Y Z Z Y Z Z Y Z F Z --+-= -----------------------(2分)()()()Y Z H Z F Z =12212z Z --=+-2222Z Z Z =+- -----------------------(2分) ()2(2)(1)H Z Z Z Z Z =+-21413132Z Z =⋅+⋅-+ -----------------------(2分) 24()3132Z Z H Z Z Z =⋅+⋅-+ -----------------------(2分)24()[(2)]()33k h k k ε=+⋅- -----------------------(2分)4. 已知02,()0,F jw ωωωω⎧<⎪=⎨>⎪⎩ ，求()F jw 的傅里叶逆变换（本题10分）解：1 ()()2j tf t F j e dωωωπ+∞=-∞⎰011j te dωωωωπ=⋅-⎰-----------------------(5分)11j tejtωωωπ=⋅⋅-2sin()ttωπ=-----------------------(5分)5. 已知某系统框图其中()()f t tε=(1) 求该系统的冲激响应()h t(2) 求该系统的零状态响应()zsy t（本题10分）解：''()3'()2()4'()()y t y t y t f t f t++=+2(32)()(41)()S S Y S S F S++=+-----------------------(2分)2()(41)()()(32)Y S SH SF S S S+==++113712S S=-⋅+⋅++-----------------------(2分)(1) 冲激响应2()[(3)7]()t th t e e tε--=-⋅+-----------------------(2分)(2)41()()()(1)(2)zsSY S H S F SS S S+=⋅=++-----------------------(1分)1117132122S S S=⋅+⋅-⋅++-----------------------(1分)零状态响应217()(3)()22t tzsy t e e tε--=+------------------------(2分)6.如图所示的电路，写出以)(tus为输入，以)(tuc为响应的微分方程。

编译原理试卷（A卷）答案__通信02一、是非题（下列各题，你认为下确的，请在题干的括号内打“√”错的打“×”。

每题2分，共10分）1、虽然名字都是用标识符表示的，但名字和标识符有着本质的区别。

…………（√）2、优先关系表所对应的优先函数，如果存在，则一定唯一。

………………（×）3、对于任何一个含有左递归的文法必存在一个等价的不含左递归的文法。

…（√）4、每个过程的DISPLAY表的体积在编译时就可确定。

……………………（√）5、一个文法的句子也一定是该文法的句型。

………………………………（√）二、填空题（每题2分，共16分）1、对文法G 的每个非终结符P，定义集合FIRSTVT（P）=（{a|P=> a…或P => Qa…，a∈V T而Q ∈V N}）。

2、如果一个文法的任何产生式的右部都不含有两个相继（并列）的非终结符，则这种文法称为（算符）文法。

3、表达式a/(b*c+d)的逆波兰表示为（abc*d+/）。

4、一张符号表的每一项（或称入口）包含两大栏，即（名字）栏和（信息）栏。

5、如果一个文法存在某个句子对应两棵不同的语法树，则称这个文法是（二义的）。

6、在一个基本块内，通常可实行的三种优化是：合并已知量、（删除多余运算）、（删除无用赋值）。

7、文法G 所产生的句子的全体是（语言），将它记为（L（G））。

8、根据优化所涉及的程序范围，优化可分为（局部）优化、（循环）优化和（全局）优化三个不同的级别。

三、名词解释题（每题3分，共15分）1、语言的语义——语言的语义是一组规则，用它可以定义一个程序的意义。

2、句型——假定G是一个文法，S是它的开始符号，如果S=>α，则称α是一个句型。

3、语法分析器——按文法的产生式识别输入的符号串是否为一个句子的分析程序。

4、语法制导翻译——在语法分析过程中，根据每个产生式所对应的语义子程序进行翻译的办法叫做语法制导翻译法。

第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。

答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。

答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。

答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。

信号与系统一、单项选择题（本大题共46分，共 10 小题，每小题 4.599999 分）1. 若一因果系统的系统函数为则有如下结论——————————（） A. 若，则系统稳定 B. 若H（s）的所有极点均在左半s平面，则系统稳定 C. 若H（s）的所有极点均在s平面的单位圆内，则系统稳定。

2. 连续信号，该信号的拉普拉斯变换收敛域为（）。

A.B.C.D.3. 连续信号与的乘积，即*=( )A.B.C.D.4. 已知f(t)，为求f(t0−at) 应按下列哪种运算求得正确结果？（式中t,a都为正值） A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t)，为求f(t0-at) 应按下列哪种运算求得正确结果？（式中t,a都为正值） A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H（s）与激励信号X（s）之间——（） A. 是反比关系； B. 无关系； C. 线性关系； D. 不确定。

7. 下列论断正确的为（）。

A. 两个周期信号之和必为周期信号； B. 非周期信号一定是能量信号； C. 能量信号一定是非周期信号； D. 两个功率信号之和仍为功率信号。

8. 的拉氏反变换为（）A.B.C.D.9. 系统结构框图如下，该系统单位冲激响应h(t)的表达式为（）A.B.C.D.10. 已知，可以求得—————（）A.B.C.D.二、多项选择题（本大题共18分，共 3 小题，每小题 6 分）1. 线性系统响应满足以下规律————————————（） A. 若起始状态为零，则零输入响应为零。

B. 若起始状态为零，则零状态响应为零。

C. 若系统的零状态响应为零，则强迫响应也为零。

D. 若激励信号为零，零输入响应就是自由响应。

2. 1．之间满足如下关系———————（）A.B.C.D.3. 一线性时不变因果系统的系统函数为H（s），系统稳定的条件是——（）A. H（s）的极点在s平面的单位圆内B. H（s）的极点的模值小于1C. H （s）的极点全部在s平面的左半平面D. H（s）为有理多项式。

长沙理工大学拟题纸课程编号 1 拟题教研室（或老师）签名 教研室主任签名 符号说明：)sgn(t 为符号函数，)(t δ为单位冲击信号，)(k δ为单位脉冲序列，)(t ε为单位阶跃信号，)(k ε为单位阶跃序列。

一、填空（共30分，每小题3分）1. 已知)()4()(2t t t f ε+=，求_______)("=t f 。

)('4)(2)("t t t f δε+ 2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ，求______)()(=*k h k f 。

}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。

0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω，则对)4(t f 取样的最大间隔是______。

m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。

101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =，试判断该系统是否为线性时不变系统______。

故系统为线性时变系统。

7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ，求该信号的傅立叶变换)(ωj F =______。

故傅立叶变换)(ωj F 不存在。

8. 已知一离散时间系统的系统函数2121)(---+=z z z H ，判断该系统是否稳定______。

故系统不稳定。

9. =+-+⎰∞∞-dt t t t )1()2(2δ______。

310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数，试问)(t f 有何种对称性______。

关于t=3的偶对称的实信号。

二、计算题（共50分，每小题10分）1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示，试由时域求解该系 统的零状态响应)(t y ，画出)(t y 的波形。

湖南工程学院测试卷〔A 、B 卷〕适用专 电子信息工 测试 闭卷 测试时间120分 业 俚 ________________ 形式 ⑷ 长度 e一、 简单计算题〔每题8分〕： 1、某连续信号f〔t 〕的傅里叶变换为到离散时间序列f〔k〕,序列f〔k〕的Z 变换.f k 12 1,2〔k 〕 1 cos — k 〔k 〕2、求序列f 1〔k 〕k 1.,2,1和2的卷积和.13、 某双边序列的Z 变换为 Z 〕10z 2 9z 2,求该 序列的时域表达式f 〔k 〕O4、 某连续系统的特征多项式为：76543 2D 〔s 〕 s 3s 6s 10s 11s 9s 6s 2试判断该系统的稳定情况,弁指出系统含有负实部、 零实部和正实部的根各有几个？ 5、某连续时间系统的系统函数为：32s 6s 4s 2〔 〕 s 3 2s 2 s 1.试给出该系统的状态方程.6、 求出下面框图所示离散时间系统的系统函数.课程名称信号与系统测试学期 得分F(j )12一根据取样间隔T 1对其进行取样得二、〔12分〕系统框图如图〔a〕,输入信号e〔t〕的时域波形如图〔b〕,子系统h〔t〕的冲激响应波形如图〔c〕所示,信「……F〔j 〕 e jn号f〔t〕的频谱为n ..y(t)f (t)图(a)h(t)1 一0 1 t图(c)试：1〕分别画出f⑴的频谱图和时域波形；2〕求输出响应y〔t〕弁画出时域波形.3〕子系统h〔t〕是否是物理可实现的？为什么？请表达理由；三〔12分〕、电路如下列图所示,鼓励信号为e〔t〕⑴, 在t=0和t=1时测得系统的输出为y⑼1, y⑴e°.5.分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应.四〔12分〕、某离散系统的差分方程为其初始状态为丫人1)2,丫人2)6,鼓励咏)也)；求：1)零输入响应丫胃的、零状态响应yzs(k)及全响应y*)；2)指出其中的自由响应分量和受迫响应分量；3)判断该系统的稳定性.五(12分)、某离散时间系统的单位函数响应kh(k) cos (k)2 o1) 1) 求其系统函数H (z)；2) 2) 粗略绘出该系统的幅频特性；3) 3) 画出该系统的框图.六、(10分)请表达弁证实z变换的卷积定理.参考答案:f(k)= (e k e 2k) (k)=((e 1)k (e 、):(k)zF(z 尸z[f(k)]=解：f i (k)={1,2,1}= (k)+2 (k 1)+ (k 2)f 1(k)* f 2(k)= f 2(k)+ 2f 2(k 1)+ f 2(k F(z)3、某双边序列的 Z 变换为 域表达式f(k)o)1 1解：Zz 0.4 z 0.5,两个单阶极点为 当收敛域为忆|>0.5 时,f(k)=(( 0.4)k 1 ( 0.5)k1) (k1) 当收敛域为 0.4<|z|<0.5 时,f(k)= ( 0.4)k 1 (k 1)+( 0.5) 当收敛域为 |z|<0.4 时,f(k)= ( 0.4)k 1 ( k)+( 0.5)k 1 ( k)点评：此题应对收敛域分别讨论,很多学生只写出第一步答案, 即只考虑单边序列.4、某连续系统的特征多项式为：7 _6 _5 _ 4 _3 _2 --D(s) s 3s 6s 10s 11s 9s 6s 2试判断该系统的稳定情况,弁指出系统含有负实部、零实部和正 实部的根各有几个？解 构作罗斯-霍维茨阵列s 7 1 6 11 6F(j1、 某连续信号f⑴的傅里叶变换为照取样间隔T 的Z 变换.1对其进行取样得到离散时间序列 ) 2~~2f(k),j3 ,按 序列f(k)F(s)s 2 3s f(t) 1(s 1)(s 2)F(z)Resi 1F(s)z 的 1 s 1K i ZsTz es s ii 1 z解法二：f(t)=L 1{F(jw)}=(ee s iT t拉普1 z 1z ee 2t ) (t) 1、 2、 和.求序列 f 1(k)k1.,2,1和f 2(k)1 cos k (k)2的卷积2)110z 2 9z 2 ,求该序列的时0.4、 0.5 k 1( k)2 i 2 s3 s 0 2由罗斯-霍维茨数列可见,元素符号弁不改变,说明s 右半平 面无极点.再由4 - 2 一 _5 3s 2 0令s 2 x 那么有2一 一 一x 3x 2 0可解得 x 1,2相应地有si , 21js 3 ,4\ 2j • 2这说明该系统的系统函数在虚轴上有四个单极点分别为土 j 及土j 2 ,系统为临界稳定.所以系统含有三个负实部的根、 四个零实部的根,无正实部的根. 点评：此题得分率很低.很多学生对全零行不知如何处理. 32 s 6s 4s25、某连续时间系统的系统函数为： s 3 2s 2 s 1.试给出该系统的状态方程. 解：系统的微分方程为y (t) 2y (t) y (t) y(t) e (t) 6e (t) 4e(t) 2e(t)取原来的辅助变量 q 及其各阶导数为状态变量弁分别表示为 q x i 、q' X 2、q'' x 3、q''' &',于是,由此微分方程立即可以写出 如下方程x i ' x 2x 2‘ 乂 3 状态方程：x 3' X i x 2 2x 3 e(t )输出方程：y x 32x i 4x 2 6x 3 x i 3x 2 4x 3 e(t)或者写成矩阵形式,上式即为x i '0 0 i x i 0 x 2' Ax Be 0 i 0 x 2 0 ex 3'i i 2 x 3 i、、I6 (0 0)此时出现全零行,有辅助多项式s 4 3s 2 2求导可得4s 3 6s,以4,6代替全零行系数.二、(12分)系统框图如图(a),输入信号e(t)的时域波 形如图(b),子系统h(t)的冲激响应波形如图(c)所示,信号f(t)的f (t)图(a)1 t图(c)分别画出f⑴的频谱图和时域波形；求输出响应y(t)弁画出时域波形.子系统h(t)是否是物理可实现的？为什么？请表达理由;解：1)根据傅立叶变换的性质得:f(t) (t 2n)nf(t)F (j )频谱为e jne(t) - --- **h(t)-y(t)试：1) 2) 3) X iy Cx De 1 3 4 x 2e(t) X 36、求出下面框图所示离散时间系统的系统函数2 1H(z) (1 ――)——角牟：z 0.3 z ।z 2.3-2Z e(t) 2图(b)h(t)F(j )2 )y(t)=[e(t) 7f(t)] h(t 户[(t+2)+2 (t)+ (t 2)]3)因h(t)是有始因果信号,所以子系统h(t)是物理可实现的. 三(12分)、电路如下列图所示,鼓励信号为 e(t) (t),在 t=0和t=1时测得系统的输出为y(0) 1, y(1) e 0.5.分别求系统 的零输入响应、零状态响应、全响应、以及自然响应和受迫响应.0.5s2)系统函数为："s' s 2 1.5s 0.5 ,特征根为1= 0.5, 2= 10.5s J 112—： 丁 ?~Y zs (s)=H(s)E(s)= s 1.5s 0.5 s = s 0.5 s 1 零状态响应：y zs (t)=(e 0.5t e t ) (t) y zs (0)=0, y zs (1)=(e 0.5 e 1)； y zi (0)= y(0) y zs (0)=1 , y zi (1)= y(1)y zs (1)= e 1 ；y zi (t)=(C 1e 0.5t +C 2e) (t),得 C 1=0, C 2=1h(t)=n( n)C=1F解：1)电路满足KVL :得 y (t) 1.5y (t) 0.5y(t) 0.5e (t)零输入响应：y zi(t)= e t (t)；全响应：y (t)= e 0.5t (t)四(12分)、某离散系统的差分方程为2y(k 2) 3y(k 1) y(k) e(k 1)其初始状态为y zi( 1) 2,y zi( 2) 6,鼓励e(k) (k)；求：1) 零输入响应y zi(k)、零状态响应y zs(k)及全响应y(k)；2)指出其中的自由响应分量和受迫响应分量；3)判断该系统的稳定性.H (z) ——n—z—解：2z 3z 1 ,特征根为1=0.5, 2=11) 1) y zi(k)=(C10.5k+C2) (k)；代入初始条件得C1= 2, C2=2零输入响应：y zi(k)= (2 20.5k) (k)Y zs(z)=H(z)E(z)=1 j-k 1 j-k-Ze 2 (k)」Z e 2 (k) 2 2Z cos(-k) (k) Z 界(k)H(z)z e"2z z 2 1z e j 22z z 2 12)系统的幅频特性为:|H(e j )1 I(e j )2 (e j )2 11 12 cos |*|H(e jw)|0.53)系统的框图六、(10分)请表达弁证实Z变换的卷积定理.解：卷积定理设Z f1(k) F1(z) , Z f2(k) F2(z),贝f]Z f〔(k)* f2(k) F1(z)F2(z)或用符号表示为：假设f1(k) F1(z), f2(k) F2(z),那么f1(k)* f2(k) F1(z)F2(z)两序列卷积后z变换的收敛区是原来两个Z变换收敛区的重叠部分.以上定理可根据卷积和及Z变换的定义证实如下k Zf1(k)*f2(k) Z f1(j)f2(k j) z f1(j)f2(k j)j k j交换上式右方的取和次序,上式成为Zf1(k)*f2(k) f1(j) z k f2(k j)j k对上式右方第二个取和式应用式(8-15)的移序特性,那么得Zf1(k)*f2(k) f1(j)z j F2(z) F1(z)F2(z)z? z z z z 1 12z* 2 3z 1 - z 1 z 0.5 z 1 (z 1)2=S-Q?5 71零状态响应：y zs(k)= (0.5k +k 1) (k)y zs(0)=0, y zs(1)=(e 0.5 e1)；全响应：y (k)= (1+k 0.5k) (k)2)自由响应:(1 0.5k) (k)受迫响应：k (k),严格地说是混合响应.3)系统的特征根为1=0.5 (单位圆内),2=1 (单位圆上),所2系统临界稳定.五(12分)、某离散时间系统的单位函数响应k h(k) cos (k)2 o1) 求其系统函数H(z)；2) 粗略绘出该系统的幅频特性；3) 画出该系统的框图.解：1)系统函数为：。