全国I卷高考理科数学分析课件
- 格式:pptx
- 大小:547.59 KB
- 文档页数:28
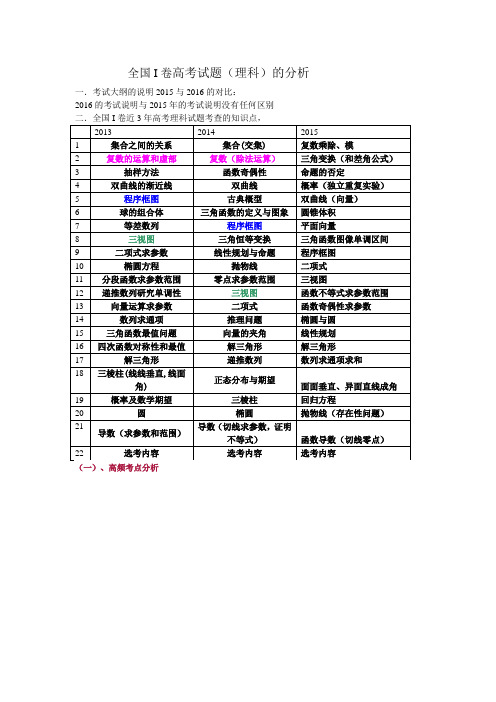
全国I卷高考试题(理科)的分析一.考试大纲的说明2015与2016的对比:2016的考试说明与2015年的考试说明没有任何区别命题规律:1.函数与导数:—3个小题,1个大题,客观题主要考查函数的基本性质、函数图像及变换、函数零点、导数的几何意义、定积分等为主,也有可能与不等式等知识综合考查;解答题主要是以导数为工具解决函数、方程、不等式等的应用问题。
2.三角函数与平面向量:小题一般主要考查三角函数的图像与性质、利用诱导公式与和差角公式、倍角公式、正余弦定理求值化简、平面向量的基本性质与运算.大题主要以正、余弦定理为知识框架,以三角形为依托进行考查(注意在实际问题中的考查)或向量与三角结合考查三角函数化简求值以及图像与性质.另外向量也可能与解析等知识结合考查.3.数列:2个小题或1个大题,小题以考查数列概念、性质、通项公式、前n项和公式等内容为主,属中低档题;解答题以考查等差(比)数列通项公式、求和公式,错位相减求和、简单递推数列为主.4.解析几何:2小1大,小题一般主要考查:直线、圆及圆锥曲线的性质为主,一般结合定义,借助于图形可容易求解.大题一般以直线与圆曲线位置关系为命题背景,并结合函数、方程、数列、不等式、导数、平面向量等知识,考查求轨迹方程问题,探求有关曲线性质,求参数范围,求最值与定值,探求存在性等问题.另外要注意对二次曲线间结合的考查,比如椭圆与抛物线,椭圆与圆等.5.立体几何:2小1大,小题必考三视图,一般侧重于线与线、线与面、面面的位置的关系以及空间几何体中的空间角、距离、面积、体积的计算的考查,另外特别注意球的组合体.解答题以平行、垂直、夹角、距离等为考查目标. 几何体以四棱柱、四棱锥、三棱柱、三棱锥等为主。
6.概率与统计:2小1大,小题一般主要考查:频率分布直方图、茎叶图、样本的数字特征、独立性检验、几何概型和古典概型、抽样(特别是分层抽样)、排列组合、二项式定理、几个重要的分布等.解答题考查点比较固定,一般考查离散型随机变量的分布列、期望和方差.仍然侧重于考查与现实生活联系紧密的应用题,体现数学的应用性.7.不等式:小题一般考查不等式的基本性质及解法(一般与其他知识联系,比如集合、分段函数等)、基本不等式性质应用、线性规划。



绝密★启用前2017年普通高等学校招生全国统一考试理科数学本试卷5页,23小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑;如需要改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x |x<1},B ={x |31x <},则 A.{|0}AB x x =<ﻩﻩB.A B =R ﻩﻩC.{|1}A B x x =>D .A B =∅【考点】:集合的简单运算,指数函数【思路】:利用指数函数的性质可以将集合B 求解出来,之后利用集合的计算求解即可。
【解析】:由310x x <⇒<,解得{}0B x x =<,故而{}{}0,1A B B x x A B A x x ⋂==<⋃==<,选A。
2.如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A.14ﻩﻩ B .π8ﻩﻩﻩC.12ﻩﻩD .π4ﻩ ﻩ【考点】:几何概型【思路】:几何概型的面积问题,=P 基本事件所包含的面积总面积。
【解析】:()21212=82r S P S r ππ==,故而选B。


2017年普通高等学校招生全国统一考试(全国I 卷)理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、 选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合{}{}131x A x x B x =<=<,,则()ﻫA.{}0=<A B x x ﻩB .A B =RC.{}1=>A B x x ﻩﻩﻩD.A B =∅ 【答案】A【解析】{}1A x x =<,{}{}310xB x x x =<=<ﻫ∴{}0AB x x =<,{}1A B x x =<,选 A2. 如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是()ﻫ ﻩﻩﻫA .14ﻩﻩB .π8C.12ﻩD.π4【答案】B【解析】设正方形边长为2,则圆半径为1则正方形的面积为224⨯=,圆的面积为2π1π⨯=,图中黑色部分的概率为π2则此点取自黑色部分的概率为ππ248=故选B3. 设有下面四个命题()ﻫ1p :若复数z 满足1z∈R ,则z ∈R ;ﻫ2p :若复数z 满足2z ∈R ,则z ∈R ;ﻫ3p :若复数12z z ,满足12z z ∈R ,则12z z =;4p :若复数z ∈R ,则z ∈R .A.13p p , B.14p p , C .23p p ,ﻩD.24p p ,【答案】B【解析】1:p 设z a bi =+,则2211a biz a bi a b -==∈++R ,得到0b =,所以z ∈R .故1P 正确;ﻫ2:p 若z =-21,满足2z ∈R ,而z i =,不满足2z ∈R ,故2p 不正确;ﻫ3:p 若1z 1=,2z 2=,则12z z 2=,满足12z z ∈R ,而它们实部不相等,不是共轭复数,故3p 不正确;4:p 实数没有虚部,所以它的共轭复数是它本身,也属于实数,故4p 正确;4. 记n S 为等差数列{}n a 的前n 项和,若4562448a a S +==,,则{}n a 的公差为() A.1B .2C .4ﻩD .8【答案】C【解析】45113424a a a d a d +=+++=61656482S a d ⨯=+=ﻫ联立求得11272461548a d a d +=⎧⎪⎨+=⎪⎩①②3⨯-①②得()211524-=d ﻫ624d =4d =∴ﻫ选C5. 函数()f x 在()-∞+∞,单调递减,且为奇函数.若()11f =-,则满足()121f x --≤≤的x 的取值范围是()A.[]22-, B.[]11-,ﻩC .[]04, D .[]13,【答案】D【解析】因为()f x 为奇函数,所以()()111f f -=-=,ﻫ于是()121f x --≤≤等价于()()()121f f x f --≤≤|ﻫ又()f x 在()-∞+∞,单调递减 121x ∴--≤≤3x ∴1≤≤ 故选D6.()62111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为ﻫA.15ﻩB .20C .30 D.35【答案】C.【解析】()()()66622111+1111x x x x x ⎛⎫+=⋅++⋅+ ⎪⎝⎭ﻫ对()61x +的2x 项系数为2665C 152⨯==ﻫ对()6211x x⋅+的2x 项系数为46C =15,∴2x 的系数为151530+= 故选C7. 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形,这些梯形的面积之和为ﻩﻩA .10ﻩﻩB.12ﻩC .14 D.16【答案】B【解析】由三视图可画出立体图ﻫ该立体图平面内只有两个相同的梯形的面 ()24226S =+⨯÷=梯6212S =⨯=全梯 故选B8. 右面程序框图是为了求出满足321000n n ->的最小偶数n ,那么在和两个空白框中,可以分别填入ﻫﻫA.1000A >和1n n =+ ﻩ B【答案】D【答案】因为要求A 大于1000时输出,且框图中在“否”时输出∴“”中不能输入A 1000>ﻫ排除A、B又要求n 为偶数,且n 初始值为0,ﻫ“”中n 依次加2可保证其为偶故选D9. 已知曲线1:cos C y x =,22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭,则下面结论正确的是()A.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2C ﻫC.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2C D.把1C 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2C 【答案】D【解析】1:cos C y x =,22π:sin 23⎛⎫=+ ⎪⎝⎭C y x首先曲线1C 、2C 统一为一三角函数名,可将1:cos C y x =用诱导公式处理.ﻫπππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x .横坐标变换需将1=ω变成2=ω,即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来ﻫ2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x .注意ω的系数,在右平移需将2=ω提到括号外面,这时π4+x 平移至π3+x ,ﻫ根据“左加右减”原则,“π4+x ”到“π3+x ”需加上π12,即再向左平移π12.10. 已知F 为抛物线C :24y x =的交点,过F 作两条互相垂直1l ,2l ,直线1l 与C 交于A 、B两点,直线2l 与C 交于D ,E 两点,AB DE +的最小值为() A .16ﻩ B .14ﻩC.12D.10【答案】A【解析】ﻫﻫ设AB 倾斜角为θ.作1AK 垂直准线,2AK 垂直x轴易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ(几何关系)(抛物线特性)ﻫcos AF P AF θ⋅+=∴ﻫ同理1cos P AF θ=-,1cos P BF θ=+ﻫ∴22221cos sin P PAB θθ==- 又DE 与AB 垂直,即DE 的倾斜角为π2θ+ﻫ2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭ﻫ而24y x =,即2P =.ﻫ∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ 21616sin 2θ=≥,当π4θ=取等号 即AB DE +最小值为16,故选A11. 设x ,y ,z 为正数,且235x y z ==,则()ﻫA.235x y z <<ﻩB .523z x y<< C .352y z x <<ﻩD.325y x z << 【答案】D【答案】取对数:ln 2ln3ln5x y ==.ﻫln33ln 22x y => ∴23x y >ﻫln2ln5x z =ﻫ则ln55ln 22x z =<ﻫ∴25x z <∴325y x z <<,故选D12. 几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是02,接下来的两项是02,12,在接下来的三项式62,12,22,依次类推,求满足如下条件的最小整数N :100N >且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A.440 B.330 C.220D .110 【答案】A【解析】设首项为第1组,接下来两项为第2组,再接下来三项为第3组,以此类推.设第n 组的项数为n ,则n 组的项数和为()12n n +ﻫ由题,100N >,令()11002n n +>→14n ≥且*n ∈N ,即N 出现在第13组之后ﻫ第n 组的和为122112nn -=--n 组总共的和为()2122212n nn n --=---若要使前N 项和为2的整数幂,则()12n n N +-项的和21k -应与2n --互为相反数ﻫ即()*21214k n k n -=+∈N ,≥ﻫ()2log 3k n =+ →295n k ==,ﻫ则()2912954402N ⨯+=+=故选A二、 填空题:本题共4小题,每小题5分,共20分。
普通高等学校招生全国统一考试(I 卷)理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合}13|{}1|{<=<=xx B x x A ,,则A. }0|{<=x x B AB. R =B AC. }1|{>=x x B AD. ∅=B A2. 如图,正方形ABCD 内的图形来自中国古代的太极图。
正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称。
在正方形内随机取一点,则此点取自黑 色部分的概率是 A.41B. 8π C.21D. 4π 3. 设有下面四个命题p1:若复数z 满足R ∈z1,则R ∈z ;p2:若复数z 满足R ∈2z ,则R ∈z ; p3:若复数z1、z2满足R ∈21z z ,则21z z =;p4:若复数R ∈z ,则R ∈z 。
其中的真命题为A. p1,p3B. p1,p4C. p2,p3D. p2,p44. 记Sn 为等差数列{an}的前n 项和,若a4 + a5 = 24,S6 = 48,则{an}的公差为A. 1B. 2C. 4D. 85. 函数f (x)在),(+∞-∞单调递减,且为奇函数。
若f (1) = 1,则满足1 ≤f (x 2) ≤ 1的x 的取值范围是A. [2,2]B. [1,1]C. [0,4]D. [1,3] 6. 62)1)(11(x x++展开式中x2的系数为 A. 15B. 20C. 30D. 357. 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形, 这些梯形的面积之和为 A. 10 B. 12 C. 14 D. 168. 右面程序框图是为了求出满足3n 2n> 1000的最小偶数n ,那么在◇和▭两个空白框中,可以分别填入 A. A > 1000和n = n + 1 B. A > 1000和n = n + 2 C. A ≤ 1000和n = n + 1 D. A ≤ 1000和n = n + 29. 已知曲线C1:x y cos =,C2:)322sin(π+=x y ,则下面结论正确的是 A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个6π单位长度,得到C2 B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个12π单位长度,得到C2 C. 把C1上各点的横坐标缩短到原来的21倍,纵坐标不变,再把得到的曲线向右平移个6π单位长度,得到C2 D. 把C1上各点的横坐标缩短到原来的21倍,纵坐标不变,再把得到的曲线向左平移个12π单位长度,得到C2 10. 已知F 为抛物线C :y2 = 4x 的焦点,过F 作两条互相垂直的直线l1、l2,直线l1与C 交于A 、B 两点,直线l2与C 交于D 、E 两点,则| AB | + | DE |的最小值为A. 16B. 14C. 12D. 1011. 设x 、y 、z 为正数,且2x = 3y = 5z ,则A. 2x < 3y < 5zB. 5z < 2x < 3yC. 3y < 5z < 2xD. 3y < 2x < 5z12. 几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。
普通高等学校招生全国统一考试全国课标I 理科数学第Ⅰ卷 (选择题 共60分)一.选择题:共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.已知集合A={x |2230x x --≥},B={x |-2≤x <2=,则A B ⋂=A .[2,1]B .[1,2)C .[1,1]D .[1,2) 2.32(1)(1)i i +-= A .1i +B .1i -C .1i -+D .1i --3.设函数()f x ,()g x 的定义域都为R ,且()f x 时奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数4.已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为A .3B .3C .3mD .3m5.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .786.如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为7.执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203B .165C .72D .1588.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则 A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-, 2p :(,),22x y D x y ∃∈+≥, 3P :(,),23x y D x y ∀∈+≤, 4p :(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ,3pB .1p ,4pC .1p ,2pD .1p ,3p10.已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个焦点,若4FP FQ =,则||QF =A .72B .52C .3D .2 11.已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为A .(2,+∞)B .(∞,2)C .(1,+∞)D .(∞,1) 12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .62B .42C .6D .4第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两个部分。