(人教版)杭州市必修第一册第三单元《函数概念与性质》测试题(有答案解析)

1

（2019）人教版高中数学必修第一册 第三章 函数概念与性质

3.1.1函数的概念

一、选择题（60分）

1．函数11yxx的值域为（ ）

A．[1, 2] B．[1,2] C．[ 262,2] D．[2,2]

2．已知函数()(0)1xafxxax，若210ax，则()fx的取值范围是（ ）

A．(22,1) B． [21,1) C．[22,1) D．(2,0)

3．函数y2019xx2018的值域是（ ）

A．0,2 B．0,2 C．1,2 D．1,2

4．函数(1)yxxx的定义域为（ ）

A．|0xx B．|1xx C．|10xx D．|01xx

5．已知函数242txtfxx在区间［－1,2］上的最大值为2，则t的值等于（ ）

A．2或3 B．－1或3 C．1 D．3

6．设函数2()(0)fxaxbxca的定义域为D，若所有点构成一个正方形区域，则a的值为（ ）

A．2 B．4 C． D．8

7．已知定义在0,上的函数fx满足2fxfxx，且当0,2x时,8fxx，则93f（ ）.

A．2019 B．2109 C．2190 D．2901

8．记号[x]表示不超过实数x的最大整数，若2()[30]30xfxx，则1232930fffff的值为（ ）

A．899 B．900 C．901 D．902 2

9．函数21222fxxxxx的最大值为（ ）．

A．2 B．32 C．52 D．2

word

- 1 - / 10 第三章单元测试卷 一、单项选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的)

1．函数f(x)＝x－1x－2的定义域为( )

A．(1，＋∞) B．[1，＋∞)

C．[1,2) D．[1,2)∪(2，＋∞)

2．德国数学家狄利克雷在数学上做出了名垂史册的重大贡献，函数D(x)＝ 0，x∉Q1，x∈Q是以他名字命名的函数，则D(D(π))＝( )

A．1 B．0

C．πD．－1

3．已知f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝2x2－2x＋1，则f(－1)＝( )

A．3 B．－3

C．2 D．－2

4．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝f－x2x＋1的定义域是( )

A．[－4,0] B．[－4,0)

C．[－4，－1)∪(－1,0] D．(－4,0)

5．若幂函数y＝(m2－3m＋3)xm－2的图象不过原点，则m的取值X围为( )

A．1≤m≤2 B．m＝1或m＝2

C．m＝2 D．m＝1

6．已知函数f(x)是定义在R上的偶函数，x≥0时，f(x)＝x2－2x，则函数f(x)在R上的解析式是( )

A．f(x)＝－x(x－2) B．f(x)＝x(|x|－2)

C．f(x)＝|x|(x－2) D．f(x)＝|x|(|x|－2)

7．已知函数f(x)＝ x2＋1，x≤0，1，x>0，若f(x－4)>f(2x－3)，则实数x的取值X围是( )

A．(－1，＋∞) B．(－∞，－1) word

- 2 - / 10 C．(－1,4) D．(－∞，1)

8．甲、乙二人从A地沿同一方向去B地，途中都使用两种不同的速度v1与v2(v1

二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)

1 单元素养检测(二)(第三章)

(120分钟 150分)

一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求的)

1．已知函数f(x)由下表给出，则f[f(3)]等于( )

x 1 2 3 4

f(x) 2 3 4 1

A．1 B．2 C．3 D．4

【解析】选A.因为f(3)＝4，所以f[f(3)]＝f(4)＝1.

2．函数f(x)在区间[－2，5]上的图象如图所示，则此函数的最小值、最大值分别是( )

A．－2，f(2) B．2，f(2)

C．－2，f(5) D．2，f(5)

【解析】选C.由函数最值的几何意义知，当x＝－2时，有最小值－2；当x＝5时有最大值f(5).

3．已知f(x)是一次函数，且f(x－1)＝3x－5，则f(x)的解析式为( )

A．f(x)＝3x＋2 B．f(x)＝3x－2

C．f(x)＝2x＋3 D．f(x)＝2x－3

【解析】选B.设f(x)＝kx＋b(k≠0)，

所以f(x－1)＝k(x－1)＋b＝3x－5，

即kx－k＋b＝3x－5，

所以k＝3，b－k＝－5， 解得k＝3，b＝－2，

所以f(x)＝3x－2.

4．下列各组函数中，表示同一函数的是( )

A．f(x)＝x＋1 x－1 ，g(x)＝x2－1

B．f(x)＝x2 ，g(x)＝(x )2 2 C．f(x)＝x2－1x－1 ，g(x)＝x＋1

D．f(x)＝x2，g(x)＝3x6

【解析】选D.A.f(x)的定义域为[1，＋∞)，g(x)的定义域为(－∞，－1]∪[1，＋∞)，故不是同一函数；

B．f(x)的定义域为R，g(x)的定义域为[0，＋∞)，故不是同一函数；

C．f(x)的定义域为{x|x≠1}，g(x)的定义域为R，故不是同一函数；

D．f(x)的定义域为R，g(x)的定义域为R，且两函数解析式化解后为同一解析式．

高一数学必修一第一册提优卷

第三章《函数的概念与性质》（一）

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)

1．下列函数中，表示同一个函数的是（ ）

A．2yx与4yx

B．11yxx与21yx

C．xyx与1010xyx D．2yx与2Sa

2．函数1()2xfxx的定义域为（ ）

A．[1,2)(2,) B．(1,) C．1,2 D．[1,)

3.已知幂函数fx的图像经过点22,2，则下列正确的是（ ）

A. fxfx B. 12120xxfxfx （其中12xx）

C. fxfx D. 12120xxfxfx（其中12xx）

4．己知函数(1)yfx＝＋的定义域是[12]－，，则函数()yfx＝－的定义域为（ ）

A．3,0 B．[1,2] C．[0,3] D．[2,1]

5. （2020天津卷）.函数241xyx的图象大致为（ ）

A B

C. D．

6．函数26,[1,2]()7,[1,1)xxfxxx，则()fx的最大值和最小值分别为（ ）

A．10，6 B．10，8 C．8，6 D．10，7

7．若函数222,0(),0xxxfxxaxx为奇函数，则实数a的值为（ ）

A．2 B．2 C．1 D．1

8. 已知fx是定义在R上的增函数，若yfx的图象过点2,1A和3,1B，则满足111fx的x的取值范围是（ ）

A．2,3 B．3,2 C．1,4 D．1,1

湖南武冈二中2021-2022学年高一上学期数学第三章函数的概念与性质单元测试人教版（2019）必修第一册

考试范围：第三章函数的概念与性质；考试时间：100分钟；命题人：邓

注意事项：

1．答题前填写好自己的姓名、班级、考号等信息

2．请将答案正确填写在答题卡上

第I卷（选择题）

一、单选题(共40分)

1．(本题4分)已知fx是一次函数，22315,2011ffff，则fx（ ）

A．32x B．32x C．23x D．23x

2．(本题4分)函数221yxx，2,2x，则（ ）

A．函数有最小值0，最大值9 B．函数有最小值2，最大值5

C．函数有最小值2，最大值9 D．函数有最小值0，最大值5

3．(本题4分)下列各组函数fx与gx的图象相同的是（ ）

A．2,fxxgxx B．22,1fxxgxx

C．01,fxgxx D．,0,,0xxfxxgxxx

4．(本题4分)已知函数Mfx的定义域为实数集R，满足1,=0,MxMfxxM（M是R的非空子集），在R上有两个非空真子集A，B，且AB，则11ABABfxFxfxfx的值域为（

）

A．20,3 B．1 C．12,,123 D．1,13

5．(本题4分)已知函数()yfx的定义域为1,2，则函数(2)yfx的定义域为（ ）

A．3,0 B．(3,0) C．3,0 D．3,0

6．(本题4分)若232a，233b，2312c，231()3d，则a，b，c，a的大小关系是（ ）

A．abcd B．badc C．bacd D．abdc

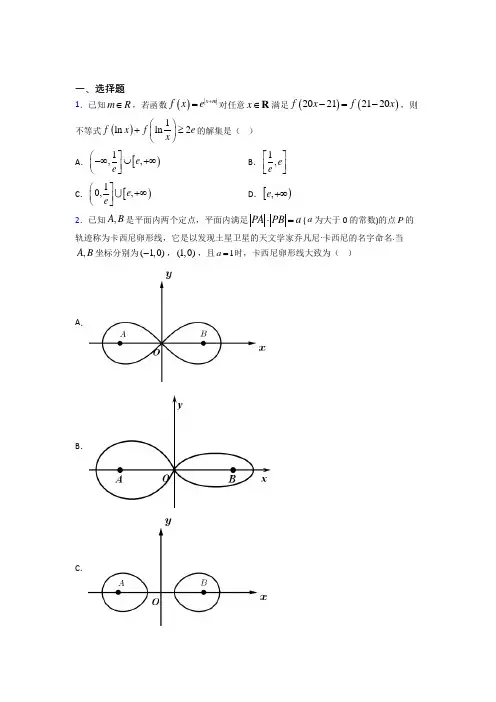
一、选择题

1．已知mR，若函数||xmfxe对任意xR满足20212120fxfx，则不等式1lnln2fxfex的解集是（ ）

A．1,,ee B．1,ee

C．10,,ee D．,e

2．已知,AB是平面内两个定点，平面内满足PAPBa(a为大于0的常数)的点P的轨迹称为卡西尼卵形线，它是以发现土星卫星的天文学家乔凡尼·卡西尼的名字命名.当,AB坐标分别为(1,0)，(1,0)，且1a时，卡西尼卵形线大致为（ ）

A．

B．

C． D．

3．奇函数()fx在(0)，内单调递减且(2)0f，则不等式(1)()0xfx的解集为（ ）

A．,21,02, B．2,12,

C．,22, D．,21,00,2

4．对于实数a和b，定义运算“*”：,,,.bababaab设fxx，224gxxx，则Mxfxgx的最小值为（ ）

A．0 B．1 C．2 D．3

5．若函数fx同时满足：①定义域内存在实数x，使得0fxfx；②对于定义域内任意1x，2x，当12xx时，恒有12120xxfxfx；则称函数fx为“DM函数”．下列函数中是“DM函数”的为（ ）

A．3fxx B．sinfxx C．1xfxe D．lnfxx

6．设函数fx的定义域为R，112fxfx，当0,1x时，1fxxx.若存在,xm，使得364fx有解，则实数m的取值范围为（ ）

A．1,2 B．3,2

高一数学必修1第三章《指数函数、对数函数和幂函数》测练题

（满分：150分；考试时间：100分钟）

一、选择题（本大题共10小题. 每小题5分，共50分.在每小题给出的四个选项中，只有一个项是符合

题目要求的）

1．指数函数y=ax的图像经过点（2，16）则a的值是 （ ）

A．41 B．21 C．2 D．4

2．化简)31()3)((656131212132bababa的结果 （ ）

A．a6 B．a C．a9 D．29a

3．在区间),0(上不是增函数的是 ( )

A.2xy B.xylog2 C.xy2 D.122xxy

4．式子82log9log3的值为 ( )

A.23 B.32 C.2 D.3

5．已知0ab，下面四个等式中：①lg()lglgabab； ②lglglgaabb；③babalg)lg(212 ；

④1lg()log10abab．其中正确命题的个数为 ( )

A．0 B．1 C．2 D．3

6．已知2log0.3a，0.32b，0.20.3c，则cba,,三者的大小关系是（ ）

A．acb B．cab C．cba D．abc

7．已知函数)(xfy的反函数)21(log)(211xxf，则方程1)(xf的解集是（ ）

1 人教A版高一数学必修第一册《函数的概念与性质》单元练习题卷（共22题）

一、选择题（共10题）

1. 已知函数 𝑓(𝑥)={−√𝑥,𝑥≥0(𝑥−1𝑥)4,𝑥<0，则 𝑓[𝑓(2)]= (  )

A． 14 B． 12 C． 2 D． 4

2. 已知函数 𝑓(𝑥) 是定义在 𝐑 上的奇函数，当 𝑥∈(−∞,0] 时，𝑓(𝑥)=−𝑥2+2𝑥，若实数 𝑚 满足 𝑓(log2𝑚)≤3，则 𝑚 的取值范围是 (  )

A． (0,2] B． [12,2] C． (0,8] D． [18,8]

3. 已知函数 𝑓(𝑥) 的定义域为 (0,+∞)，且在 (0,+∞) 上单调递增，则不等式 𝑓(𝑥)>𝑓(2𝑥−3) 的解集是 (  )

A． (−∞,3) B． (3,+∞) C． (0,3) D． (32,3)

4. 定义在 𝐑 上的函数 𝑓(𝑥) 满足 𝑓(𝑥+2)=12𝑓(𝑥)，当 𝑥∈[0,2] 时，𝑓(𝑥)={12−2𝑥,0≤𝑥<1−21−∣𝑥−32∣,1≤𝑥<2，函数 𝑔(𝑥)=𝑥3+3𝑥2+𝑚．若对任意 𝑠∈[−4,−2)，存在 𝑡∈[−4,−2)，不等式 𝑓(𝑠)−𝑔(𝑡)≥0 成立，则实数 𝑚 的取值范围是 (  )

A． (−∞,−12] B． (−∞,14]

C． (−∞,8] D． (−∞,312]

5. 函数 𝑓(𝑥)=𝑥，𝑔(𝑥)=𝑥2−𝑥+3，若存在 𝑥1,𝑥2,⋯,𝑥𝑛∈[0,92]，使得 𝑓(𝑥1)+𝑓(𝑥2)+⋯+𝑓(𝑥𝑛−1)+𝑔(𝑥𝑛)=𝑔(𝑥1)+𝑔(𝑥2)+⋯+𝑔(𝑥𝑛−1)+𝑓(𝑥𝑛)，则 𝑛 的最大值为 (  )

A． 7 B． 8 C． 9 D． 10

1 人教A版高一数学必修第一册《函数的概念与性质》单元练习题卷（共22题）

一、选择题（共10题）

1. 若函数 𝑓(𝑥)={𝑥2+1,𝑥≤1lg𝑥,𝑥>1，则 𝑓(𝑓(10))= (  )

A． lg101 B． 2 C． 1 D． 0

2. 已知 𝑓(𝑥)，𝑔(𝑥) 都是偶函数，且在 [0,+∞) 上单调递增，设函数 𝐹(𝑥)=𝑓(𝑥)+𝑔(1−𝑥)−∣𝑓(𝑥)−𝑔(1−𝑥)∣，若 𝑎>0，则 (  )

A．𝐹(−𝑎)≥𝐹(𝑎) 且 𝐹(1+𝑎)≥𝐹(1−𝑎)

B．𝐹(−𝑎)≥𝐹(𝑎) 且 𝐹(1+𝑎)≤𝐹(1−𝑎)

C．𝐹(−𝑎)≤𝐹(𝑎) 且 𝐹(1+𝑎)≥𝐹(1−𝑎)

D．𝐹(−𝑎)≤𝐹(𝑎) 且 𝐹(1+𝑎)≤𝐹(1−𝑎)

3. 如图所示的曲线是幂函数 𝑦=𝑥𝛼 在第一象限内的图象．已知 𝛼 分别取 −1，1，12，2 四个值，则与曲线 𝐶1，𝐶2，𝐶3，𝐶4 相应的 𝛼 依次为 (  )

A． 2，1，12，−1 B． 2，−1，1，12 C． 12，1，2，−1 D． −1，1，2，12

4. 已知函数 𝑓(𝑥)={1,𝑥≤01𝑥,𝑥>0，则使方程 𝑥+𝑓(𝑥)=𝑚 有解的实数 𝑚 的取值范围是 (  )

A．(1,2) B．(−∞,−2]

C．(−∞,1)∪(2,+∞) D．(−∞,1]∪[2,+∞)

5. 已知函数 𝑓(𝑥)=∣𝑥+2∣，𝑔(𝑥)=∣𝑥+𝑡∣，定义函数 𝐹(𝑥)={𝑓(𝑥),当 𝑓(𝑥)≤𝑔(𝑥)𝑔(𝑥),当 𝑓(𝑥)>𝑔(𝑥)，若对任意的

𝑥∈𝐑，都有 𝐹(𝑥)=𝐹(2−𝑥) 成立，则 𝑡 的取值为 (  )

A． −4 B． −2 C． 0 D． 2

1 人教A版高一数学必修第一册《函数的概念与性质》单元练习题卷（共22题）

一、选择题（共10题）

1. 函数 𝑦=(2𝑚−1)𝑥+𝑏 在 𝐑 上是减函数，则 (  )

A． 𝑚>12 B． 𝑚<12 C． 𝑚>−12 D． 𝑚<−12

2. 已知函数 𝑓(𝑥) 的定义域是 (0,+∞)，且满足 𝑓(𝑥𝑦)=𝑓(𝑥)+𝑓(𝑦)，𝑓(12)=1，对任意 0<𝑥<𝑦，都有 𝑓(𝑥)>𝑓(𝑦)，则不等式 𝑓(−𝑥)+𝑓(3−𝑥)≥−2 的解集为 (  )

A． {𝑥∣ −1≤𝑥<0或3<𝑥≤4}

B． {𝑥∣ −4≤𝑥<0}

C． {𝑥∣ 3≤𝑥≤4}

D． {𝑥∣ −1≤𝑥<0}

3. 已知函数 𝑓(𝑥)={lg𝑥,𝑥>0𝑥+12,𝑥≤0，则 𝑓(𝑓(−2))= (  )

A． −3 B． 0 C． 1 D． −1

4. 下列四组函数中，两个函数相同的是 (  )

A． 𝑦=√𝑥2 和 𝑦=(√𝑥)2

B． 𝑦=1 和 𝑦=𝑥0

C． 𝑦=𝑥(𝑥∈{0,1}) 和 𝑦=𝑥2(𝑥∈{0,1})

D． 𝑦=log𝑎𝑥2 和 𝑦=2log𝑎𝑥

5. 若一系列函数的解析式相同，值域相同但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为 𝑦=𝑥2−2𝑥+1，值域为 {0,4,16} 的“孪生函数”共有 (  )

A． 4 个 B． 5 个 C． 8 个 D． 9 个

6. 下列函数中与函数 𝑦=𝑥 是同一函数的是 (  )

A． 𝑦=∣𝑥∣ B． 𝑦=√𝑥2 C． 𝑦=(√𝑥)2 D． 𝑦=√𝑥33

7. 函数 𝑦=√1−𝑥 的定义域是 (  )

A． [1,+∞) B． (−∞,1] C． [0,+∞) D． (−∞,0]

1 人教A版高一数学必修第一册《函数的概念与性质》单元练习题卷（共22题）

一、选择题（共10题）

1. 设 𝐷 是含数 1 的有限实数集，𝑓(𝑥) 是定义在 𝐷 上的函数．若 𝑓(𝑥) 的图象绕原点逆时针旋转

π6 后与原图象重合，则在以下各项中，𝑓(1) 的可能取值只能是 (  )

A． √3 B． √32 C． √33 D． 0

2. 如果函数 𝑓(𝑥)=12(𝑚−2)𝑥2+(𝑛−8)𝑥+1(𝑚≥0,𝑛≥0) 在区间 [12,2] 上单调递减，那么 𝑚𝑛

的最大值为 (  )

A．16 B．18 C．25 D．812

3. 定义“函数 𝑦=𝑓(𝑥) 是 𝐷 上的 𝑎 级类周期函数”如下：函数 𝑦=𝑓(𝑥)，𝑥∈𝐷，对于给定的非零常数 𝑎，总存在非零常数 𝑇，使得定义域 𝐷 内的任意实数 𝑥 都有 𝑎𝑓(𝑥)=𝑓(𝑥+𝑇) 恒成立，此时 𝑇 为 𝑓(𝑥) 的周期．若 𝑦=𝑓(𝑥) 是 [1,+∞) 上的 𝑎 级类周期函数，且 𝑇=1，当 𝑥∈[1,2) 时，𝑓(𝑥)=2𝑥+1，且 𝑦=𝑓(𝑥) 是 [1,+∞) 上的单调递增函数，则实数 𝑎 的取值范围为

(  )

A． [56,+∞) B． [2,+∞) C． [53,+∞) D． [10,+∞)

4. 下列函数中，既是偶函数又在 (0,+∞) 上单调递增的函数是 (  )

A． 𝑦=cos𝑥 B． 𝑦=𝑥3 C． 𝑦=log12𝑥 D． 𝑦=ex+e−x

5. 若函数 𝑓(𝑥)(𝑥∈𝐑) 为奇函数，𝑓(1)=12，𝑓(𝑥+2)=𝑓(𝑥)+𝑓(2)，则 𝑓(5)= (  )

A． 0 B． 1 C． 52 D． 5

6. 设函数 𝑓(𝑥)={𝑥2+1,𝑥≤12𝑥,𝑥>1，则 𝑓(𝑓(3)) 等于 (  )

一、选择题

1．已知mR，若函数||xmfxe对任意xR满足20212120fxfx，则不等式1lnln2fxfex的解集是（

）

A．1,,ee B．1,ee

C．10,,ee D．,e

2．已知函数2265mmmfxx是幂函数，对任意1x，20,x，且12xx，满足12120fxfxxx，若a，bR，且0ab，则fafb的值（ ）

A．恒大于0 B．恒小于0 C．等于0 D．无法判断

3．已知奇函数fx在区间2,3上单调递增，则fx在区间3,2上（ ）

A．单调递增，且最大值为2f B．单调递增，且最大值为3f

C．单调递减，且最大值为2f D．单调递减，且最大值为3f

4．函数32241xxxxy的部分图像大致为（ ）

A．

B．

C．

D． 5．函数fx对于任意xR，恒有12fxfx，那么（ ）

A．可能不存在单调区间 B．fx是R上的增函数

C．不可能有单调区间 D．一定有单调区间

6．已知函数2()fxxbxc，且(2)()fxfx，则下列不等式中成立的是（ ）

A．(4)(0)(4)fff B．(0)(4)(4)fff

C．(0)(4)(4)fff D．(4)(0)(4)fff

7．已知函数2()2+1,[0,2]fxxxx，函数()1,[1,1]gxaxx，对于任意1[0,2]x，总存在2[1,1]x，使得21()()gxfx成立，则实数a的取值范围是（ ）

A．(,3] B．[3,) C．(,3][3,) D．(,3)(3,)

《函数概念与性质》综合测试卷

一、单选题

1．（2019·浙江南湖 嘉兴一中高一月考）下列四组函数中,fx与gx表示同一函数是（ ）

A．1fxx,211xgxx B．1fxx,1,11,1xxgxxx

C．1fx,01gxx D．33fxx,2gxx

2．（2020·浙江高一课时练习）已知2()fxxx,则(1)fx等于（ ）

A．21xx B．2xx C．221xx D．22xx

3．（2020·浙江高一课时练习）函数234xxyx的定义域为

A．[4,1] B．[4,0) C．(0,1] D．[4,0)(0,1]

4．（2020·全国高一课时练习）下列函数fx中,满足对任意12,0,xx,当x1

A．2fxx B．1fxx

C．fxx D．21fxx

5．（2020·浙江高一课时练习）若x为实数,则函数235yxx的值域为（ ）

A．(,) B．[0,) C．[7,) D．[5,)

6．（2020·全国高一课时练习）函数(21)ymxb在R上是减函数．则（ ） 2 A．12m B． 12m C．12m D．12m

7．（2020·全国高一课时练习）若函数(31)4,1,1axaxfxaxx,是定义在R上的减函数,则a的取值范围为（ ）

A．11,83 B．10,3

C．1,8 D．11,,83

8．（2019·浙江高一期中）已知函数222,0()1,0xxfxxxx,则()fx的最大值是( )

A．222 B．222 C．1 D．1

一、选择题

1．下列各组函数中，表示同一个函数的是（ ）

A．211xyx与1yx B．yx与logxaya（0a且1a）

C．21yx与1yx D．lgyx与21lg2yx

2．函数12xy的大致图象是（ ）.

A． B．

C． D．

3．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微：数形结合百般好，隔离分家万事休”．在数学学习中和研究中，常用函数的图象来研究函数的性质，页常用函数的解析式来琢磨函数图象的特征，如函数22xyxxR的大致图象是（ ）

A． B． C． D．

4．已知函数3,<1log,1aaxaxfxxx的值域．．是R，那么实数a的取值范围是（ ）

A．31,2 B．1, C．0,11,3 D．3,32

5．已知函数22()lg[(1)(1)1]fxaxax的值域为R．则实数a的取值范围是（ ）

A．5[1,]3 B．5(1,]3

C．5,1(,)3 D．5,1[1,)3

6．已知：23log2a，42log3b，232c，则a，b，c的大小关系是（ ）

A．bca B．bac C．cba D．cab

7．函数212()log4fxx的单调递增区间为（ ）.

A．(0,+) B．(-,0) C．(2,+) D．(-,-2)

8．已知函数()fx是定义在R上的单调递增的函数，且满足对任意的实数x都有[()3]4xffx，则()()fxfx的最小值等于（ ）.

A．2 B．4 C．8 D．12

9．函数1()1xfxa恒过定点（ ）

A．(1,1) B．(1,1) C．(1,0) D．(1,1)

1 人教A版高一数学必修第一册《函数的概念与性质》单元练习题卷（共22题）

一、选择题（共10题）

1. 已知不等式 𝑎𝑥2−𝑥+𝑐>0 的解集为 {𝑥∣ −2<𝑥<1}，则函数 𝑦=𝑎𝑥2+𝑥+𝑐 的图象大致为

(  )

A． B．

C． D．

2. 已知函数 𝑓(𝑥) 为定义在 𝐑 上的奇函数，当 𝑥<0 时，𝑓(𝑥)=𝑥(𝑥−1)，则 𝑓(2)= (  )

A． −6 B． 6 C． −2 D． 2

3. 十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用，后来英国数学家哈利奥特首次使用“<”和“>”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远．若 𝑎,𝑏,𝑐∈𝐑，则下列命题正确的是 (  )

A．若 𝑎𝑏≠0 且 𝑎<𝑏，则 1𝑎>1𝑏

B．若 𝑎>𝑏>0，则 𝑏+1𝑎+1>𝑏𝑎

C．若 𝑎+𝑏=2，则 𝑎𝑏<1

D．若 𝑐<𝑏<𝑎 且 𝑎𝑐<0，则 𝑐𝑏2<𝑎𝑏2

4. 定义全集 𝑈 的子集 𝐴 的特征函数 𝑓𝐴(𝑥)={1,𝑥∈𝐴0,𝑥∉𝐴，对于任意的集合 𝐴,𝐵⊆𝑈，下列说法错误的是 (  )

A．若 𝐴⊆𝐵，则 𝑓𝐴(𝑥)≤𝑓𝐵(𝑥)，对于任意的 𝑥∈𝑈 成立

2 B． 𝑓𝐴∩𝐵(𝑥)=𝑓𝐴(𝑥)𝑓𝐵(𝑥)，对于任意的 𝑥∈𝑈 成立

C． 𝑓𝐴∪𝐵(𝑥)=𝑓𝐴(𝑥)+𝑓𝐵(𝑥)，对于任意的 𝑥∈𝑈 成立

D．若 𝐴=∁𝑈𝐵，则 𝑓𝐴(𝑥)+𝑓𝐵(𝑥)=1，对于任意的 𝑥∈𝑈 成立

5. 已知 −π2<𝛼<0，sin𝛼+cos𝛼=15，则 1cos2𝛼−sin2𝛼= (  )

一、选择题

1．已知()fx是R上的奇函数，()gx是R上的偶函数，且32()()231fxgxxxx，则(1)(2)fg（ ）

A．5 B．6 C．8 D．10

2．若奇函数()fx在区间3,6上是增函数，且在区间3,6上的最大值为7，最小值为-1，则263ff的值为（ ）

A．5 B．-5 C．13 D．-13

3．函数fx对于任意xR，恒有12fxfx，那么（ ）

A．可能不存在单调区间 B．fx是R上的增函数

C．不可能有单调区间 D．一定有单调区间

4．函数()||fxxxa在区间(0,1)上既有最大值又有最小值，则实数a的取值范围是（ ）

A．[222,0) B．(0,222]

C．2,12 D．[222,1)

5．已知定义在R上的奇函数fx满足：当0,1x时，31xfx，则1f=（ ）

A．2 B．1 C．-2 D．-1

6．已知定义在R上的奇函数f(x)满足f(x－4)＝－f(x)，且在区间[0，2]上是增函数，若方程f(x)＝m(m>0)在区间[－8，8]上有四个不同的根x1，x2，x3，x4，则x1＋x2＋x3＋x4等于（ ）

A．－6 B．6

C．－8 D．8

7．函数f(x)＝2112xx的值域为( )

A．[－43,43] B．[－43,0]

C．[0,1] D．[0,43]

8．给出定义：若1122mxm（其中m为整数），则m叫做离实数x最近的整数，记作,xxm即．在此基础上给出下列关于函数的四个命题： ①11()22f；②(3.4)0.4f；③11()()44ff；④()yfx的定义域是R，值域是11,22；则其中真命题的序号是 （ ）

A．①② B．①③ C．②④ D．③④