电阻的微观理论和超导体讲义
- 格式:ppt
- 大小:5.09 MB
- 文档页数:56
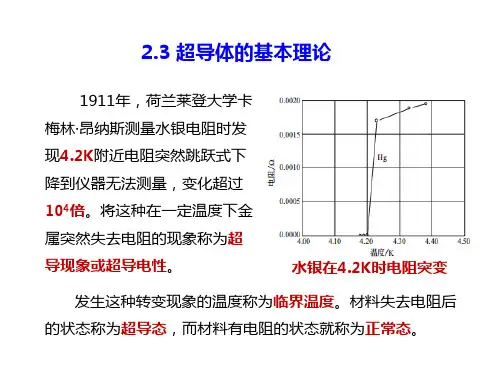


超导体电阻率
摘要:
1.超导体的定义与特性
2.超导体的电阻率
3.超导体的应用领域
4.我国在超导领域的发展
正文:
一、超导体的定义与特性
超导体,是指在低温下电阻为零的金属或合金材料。
当超导体的温度降至临界温度以下时,其电阻会突然变为零,表现出超导现象。
超导体具有零电阻和完全磁通排斥的特性,因此在许多领域具有广泛的应用前景。
二、超导体的电阻率
超导体的电阻率是衡量其导电性能的重要指标。
在超导状态下,超导体的电阻率小于10^-25Ω·m,远低于传统导体的电阻率。
这一特性使得超导体能够在电流通过时不产生热量,从而实现高效、低能耗的输电。
三、超导体的应用领域
超导体在许多领域具有广泛的应用前景,包括但不限于以下几个领域:
1.超导输电:利用超导体进行远距离、高功率的输电,可实现高效、低能耗的电力传输。
2.超导磁体:超导体在磁体领域具有重要应用,如制造粒子加速器、核磁共振成像仪等高精度科学仪器。
3.超导传感器:超导体的高灵敏度和低噪声特性使其在传感器领域具有广泛应用,如制作量子计算设备等。
4.超导能量存储系统:利用超导体制作超级电容器和超导电池等能量存储设备,可实现高效、紧凑的能源存储。
四、我国在超导领域的发展
我国在超导领域取得了举世瞩目的成果。
从20 世纪50 年代开始,我国便启动了超导研究的国家计划。
近年来,我国在高温超导材料、超导磁体、超导输电等方面取得了一系列重大突破,成为全球超导研究的重要力量。
综上所述,超导体具有独特的零电阻特性,使其在多个领域具有广泛的应用前景。


超导现象的巨观和微观理论解释超导是物理学中一种引人注目的现象,指的是一些物质在低温下表现出完全无电阻的特性。
超导现象的原理一直是科学家们研究的焦点之一,对于揭示其微观机制和应用于实际中具有重要意义。
本文将从巨观和微观两个层面探讨超导现象的理论解释。
首先,我们从巨观层面入手,观察超导现象的整体特性和性质。
当某些物质被冷却到一个临界温度以下时,就会出现超导现象。
在超导状态下,电流可以无损耗地在材料内部流动,这意味着电流可以在超导体内无限延续下去而不会受到阻力。
这种特性使得超导材料在电力输送、电子器件制造等领域具有广泛的应用潜力。
对于超导现象的巨观解释,目前最被广泛接受的理论是BCS理论,即“巴丁-库珀-斯坦因理论”。
BCS理论认为,超导是由于电子与晶格振动之间的相互作用导致的。
在低温下,晶格振动会形成一种被称为“库珀对”的特殊态,电子通过与这些库珀对的相互作用而形成一个整体,从而形成了超导现象。
BCS理论的核心是超导能隙的形成。
超导能隙是指在超导体中,电子必须具有一定的能量以克服超导材料产生的能隙才能从一个能级跃迁到另一个能级。
这就是为何只有在低温下才能观察到超导现象。
超导能隙的形成和库珀对的形成密切相关,库珀对提供了足够的能量使电子跃迁,进而产生超导现象。
接下来,我们来探讨超导现象的微观解释。
超导的微观机制可以从电子的运动和相互作用的角度进行解释。
在超导材料中,电子之间存在相互排斥的库伦力,这会导致电子在晶格中受到散射,并且能量会损失到晶格中去。
然而,在低温下,电子与晶格振动的相互作用会导致电子和晶格之间的相互作用具有吸引力,形成库珀对。
库珀对的形成是超导现象的关键步骤。
正常情况下,库伦排斥力会使得电子间的相互作用能增加,从而阻碍超导的发生。
但在超导材料中,晶体格子振动引起的吸引力抵消了库伦排斥力,形成了库珀对。
这种库珀对是由电子和晶格共同参与的量子态,具有特殊的运动和相互作用方式。
库珀对的产生降低了电子之间的相互作用能,使得电子可以在超导材料中自由地流动而不受到散射的干扰。

高三物理 欧姆定律、电阻定律、半导体、超导体及应用 知识精讲 通用版【本讲主要内容】欧姆定律、电阻定律、半导体、超导体及应用1. 知道形成电流的条件,理解电流的概念。
2. 理解欧姆定律的内容和适用条件。
3. 理解电阻定律的内容、公式,电阻率的意义、线性元件及非线性元件。
4. 知道半导体、超导体及其应用。
【知识掌握】【知识点精析】1. 电流(1)定义:电荷的定向移动形成电流。
电荷指自由电荷,金属导体中指自由电子的定向移动,电解质溶液中指正负离子同时向相反方向的运动。
(2)形成电流的条件:导体两端存在电压。
其一要有自由电荷;其二要有电场。
电源的作用就是保持导体两端的持续的电压,形成持续的电流。
(3)电流的方向:规定正电荷定向移动的方向为电流的方向。
如果电流是靠自由电子的定向移动形成的,则电流的方向和自由电子的定向移动方向相反。
(4)电流强度:通过导体某横截面的电荷量Q 跟通过这些电荷量所用时间t 的比值叫电流强度,简称电流。
定义式tQ I =,其中Q 是通过导体横截面的电量 。
(5)单位:安培(A )是国际单位制的基本单位之一 A 10mA 10A 163μ==。
(6)方向不随时间改变的电流叫直流;方向和强弱都不随时间改变的电流叫恒定电流。
(7)电流的微观本质:如图是粗细均匀的一段长为L 的导体,两端加上一定的电压,导体中的自由电荷沿导体定向移动的速率为V ,设导体的横截面积为S ,导体每单位体积内的电荷数为N ,每个自由电荷的电荷量为q 。
导体中的自由电荷总数为N =nSL总电荷量为Q=Nq=nLSq所有这些电荷通过横截面D 所需的时间为v L t =所以导体中的电流nqSv vL nLSq t Q I === 由此可见,从微观上讲,电流决定于导体中单位体积中的自由电荷数目,电荷量,定向移动速度,还与导体的横截面积有关。
2. 欧姆定律(1)内容:导体中的电流跟导体两端的电压成正比,跟导体的电阻成反比,即RU I =。

电阻(或电阻率)的微观理论理论一:设有一段金属导体,横截面积为S ,长为L ,在导体的两端加上电压U ,则导体中的场强LUE =.这时,一自由电子在电场力eEF =的作用下做定向移动。
设电子的质量为m,则定向移动的加速度为mLUe m eE m F a ===。
运动的自由电子要频繁地与金属正离子碰撞,使其定向移动受到破坏,限制了移动速率的增加。
自由电子在碰撞后向各个方向弹射的机会相等,失去了之前定向移动的特性,又要从新开始做初速为0的定向加速运动。
自由电子相继两次碰撞的间隔有长有短,设平均时间为t ,则自由电子在下次碰撞前的定向移动速率at v t =,那么在时间t 内的平均速率2atv =。
结合之前推出的mLUe a =,得自由电子的平均移动速率为mLUet v 2=。
代入电流的微观表达式neSv I =,得mL StUne I 22=对于一定的金属材料,在一定的温度下,t 是个确定的数值(10-14~10-12s),也就是说,对于一段金属导体,mLStne 22是个常量。
因此,导体中的电流强度I 与两端的电压U 成正比。
导体两端的电压与导体中的电流强度的比值(Stne mL22)就是这段导体的电阻,即Stne mLR 22=。
由此看出,导体的电阻与长度成正比,与横截面积成反比,与tne m22成正比(实际上对于金属导体而言,均为自由电子来导电,所以只有nt1由导体的自身特性决定)。
因此,在一定温度时,导体的电阻是SLR ρ=。
ρ是导体的电阻率。
对于一定温度与相同的导体,电阻率一定。
请根据以上叙述完成电阻率ρ的推导过程。
理论二:自由电子的定向移动可视为匀速运动,则电场力F 与金属正离子对自由电子的平均阻力f 相等,即L eU eE F f ===,电场力功率mL te U Lm Uet L Ue Fv P F 22222===,则电场力对L 长导线中所有电子的功率Lm nSt e U nLS P P F 222==,而电热功率mL nSt U e Stne mL v S e n R I P Q 2222222222===(电热功率的微观表达式),由此可知,电场力功率等于电热功率,即Q P P =,又因为金属正离子对自由电子的平均阻力LeU eE F f ===,所以阻力功率等于电场力功率,等于电热功率,即mL nStU e fvnLs P f 222==。


电阻(或电阻率)的微观理论理论一:设有一段金属导体,横截面积为S ,长为L ,在导体的两端加上电压U ,则导体中的场强LUE =.这时,一自由电子在电场力eEF =的作用下做定向移动。
设电子的质量为m,则定向移动的加速度为mLUe m eE m F a ===。
运动的自由电子要频繁地与金属正离子碰撞,使其定向移动受到破坏,限制了移动速率的增加。
自由电子在碰撞后向各个方向弹射的机会相等,失去了之前定向移动的特性,又要从新开始做初速为0的定向加速运动。
自由电子相继两次碰撞的间隔有长有短,设平均时间为t ,则自由电子在下次碰撞前的定向移动速率at v t =,那么在时间t 内的平均速率2atv =。
结合之前推出的mLUe a =,得自由电子的平均移动速率为mLUet v 2=。
代入电流的微观表达式neSv I =,得mL StUne I 22=对于一定的金属材料,在一定的温度下,t是个确定的数值(10-14~10-12s),也就是说,对于一段金属导体,mLStne 22是个常量。
因此,导体中的电流强度I 与两端的电压U 成正比。
导体两端的电压与导体中的电流强度的比值(Stne mL22)就是这段导体的电阻,即Stne mLR 22=。
由此看出,导体的电阻与长度成正比,与横截面积成反比,与tne m22成正比(实际上对于金属导体而言,均为自由电子来导电,所以只有nt1由导体的自身特性决定)。
因此,在一定温度时,导体的电阻是SLR ρ=。
ρ是导体的电阻率。
对于一定温度与相同的导体,电阻率一定。
请根据以上叙述完成电阻率ρ的推导过程。
理论二:自由电子的定向移动可视为匀速运动,则电场力F 与金属正离子对自由电子的平均阻力f 相等,即L eU eE F f ===,电场力功率mL te U Lm Uet L Ue Fv P F 22222===,则电场力对L 长导线中所有电子的功率Lm nSt e U nLS P P F 222==,而电热功率mL nSt U e Stne mL v S e n R I P Q 2222222222===(电热功率的微观表达式),由此可知,电场力功率等于电热功率,即Q P P =,又因为金属正离子对自由电子的平均阻力LeU eE F f ===,所以阻力功率等于电场力功率,等于电热功率,即mL nStU e fvnLs P f 222==。


超导体知识点超导体是一种在低温下表现出无电阻和完全磁通排斥现象的材料。
在超导体中,电流可以在没有任何耗散的情况下持续循环流动,这使得超导体在电磁学和能源应用等领域具有巨大的潜力。
本文将介绍超导体的基本概念、超导机制、超导材料和超导应用等方面的知识。
一、超导体的基本概念超导体是指在一定的温度下,电阻可以降至零的材料。
超导现象的发现可以追溯到1911年,在极低温下,荷兰物理学家海克·卡末林发现了汞的超导性。
此后,人们又陆续发现了其他材料也具有类似的特性。
二、超导机制超导现象的产生与电子之间的库仑相互作用密切相关。
在常规金属中,电子在受到温度和其它杂质的影响下会散射,从而产生电阻。
但在超导体中,电子可以通过与晶格振动相互作用,形成库伦对并在晶格中自由传输。
这种电子的凝聚状态使得电流可以在超导体中无阻力地流动。
三、超导材料超导材料可以分为低温超导体和高温超导体两类。
1. 低温超导体低温超导体需要在极低的温度下才能表现出超导特性。
常见的低温超导体包括铅(Pb)、汞(Hg)和锡(Sn)等。
2. 高温超导体高温超导体是指在相对较高的温度下表现出超导特性的材料。
这些材料通常包含氧化物,如铜氧化物(cuprate)、铁基超导体和镨钐铁钛基超导体等。
高温超导体的发现极大地推动了超导技术的发展,因为相对较高的工作温度使得超导体可以更方便地应用于实际生活中。
四、超导应用超导体在多个领域具有广泛的应用前景。
1. 能源传输超导体的无电阻特性使其成为输电线路的理想选择。
通过将输电线路用超导体替代传统的铜导线,可以大大减少能量损失。
2. 磁共振成像(MRI)超导体在医学领域的应用主要体现在磁共振成像技术中。
磁共振成像利用超导体产生的高强度磁场和射频脉冲,可以获得人体内部组织的高清影像,用于诊断和研究。
3. 磁悬浮交通超导体还可以应用于磁悬浮交通领域。
由于超导体可以在磁场中排斥磁通线,使得超导体制成的轨道可以与磁浮车辆产生浮力,从而实现摩擦减小、高速运行的效果。
电阻微观解释电阻是电学中的一个重要概念,指的是电路中电流流经某段导体时,该导体对电流的阻碍作用。
在微观层面上,电阻可以被看作是由于导体内电子的运动受到阻碍而产生的。
首先,电阻与导体内的自由电子密度有关。
在一个导体中,自由电子是带负电荷的粒子,在材料内自由行动。
然而,在实际情况下,这些自由电子会在材料内受到晶格不规则性的影响,从而产生碰撞。
这些碰撞会使电子的速度发生变化,并且会导致电流的弱化。
因此,自由电子密度越高,导体中的电阻就越小,因为电子之间的碰撞机会减少。
其次,电阻还与导体中自由电子的电荷和电子的移动速度有关。
当自由电子从低电位点移向高电位点时,在深化的电势井中将会受到引力主导势能坡的加速,然而电子在撞击晶格时也会失去一部分它们本来就有的能量。
如果电子的移动速度较低,那么这种能量损失就更明显,从而导致电阻的增加。
此外,电子的电荷量也会影响电阻的大小,因为电阻是由导体中电子受阻碍而产生的(导体中不仅有电子,还有离子),电子电荷量越大,其与离子的相互作用力就越强,因而电阻也会随之增加。
此外,在绝缘体、半导体和金属等不同类型的材料中,电阻的大小也会有所不同。
这主要是由于晶格结构不同,自由电子密度和速度也不同,从而导致电子之间的碰撞频率以及电阻的大小不同。
最后,电阻也与温度相关。
当导体温度升高时,导体内的原子的热振动加剧,使晶格更不规则,并增加电子与离子的碰撞机率。
因此,随着温度的升高,导体的电阻也会增加。
这就是为什么在大多数电子元件中,需要在散热的地方使用散热片的原因。
总之,电阻是由多个微观因素共同作用产生的,包括自由电子密度和速度、电子电荷量、材料的组成和形态等。
微观分析电阻现象,不但能更深刻地理解它的原理,还可以帮助我们更好地设计和制造各种电路元件。
3 超导体微观理论超导微观机制经典理论对超导电性产生的原因无法解释。
在量子论建立不久,F.伦敦就指出,超导环内的磁通是量子化的。
因此,超导电性是宏观世界的量子现象。
1962 年,实验证实磁通是量子化的。
同位素效应所谓同位素效应是指超导体的临界温度依赖于同位素质量的现象。
1950 年英国H.弗罗利希指出,金属中电子通过交换声子(点阵振动)可以产生吸引作用。
他预言超导体的临界温度与同位素的质量之间存在一定的关系。
所谓“临界温度”,就是导体从正常导电状态变为超导电状态时的转变温度。
果然,弗罗里希的预言得到了实验的证实。
1950 年麦克斯韦(E.Maxwell)和雷诺(C.A.Rayhold)各自独立圣测量了水银同位素的临界转变温度。
-1/2 实验发现:TC∝М 其中М为同位素质量。
同位素效应把晶格振动(其量子称为声子)与电子联系起来了,它告诉人们电子-声子的相互作用与超导电性密切相关。
弗罗利希经过分析后认为,同位素之间的电子分布状态是相同的,而原子质量是不同的,那么,超导电性会不会与晶格原子的性质有关呢?也许,超导的出现(即电阻的消失)是由于电子和晶格原子的相互作用才产生的吧!那么,电子和晶格原子是怎样互相作用的呢?弗罗里希对这一问题一筹莫展,无能为力。
空带空带p2′ EF 能隙2Δ p1′ EF 占满占满p1 q p2 T0K 下的正常态和超导态电子能谱超导能隙(energy gap of superconductors)实验证明,超导态的电子能谱与正常态不同,在费密能EF(最低激发态与基态之间)附近出现了一个半宽度为Δ能量间隙。
Δ≈10-310-4eV。
如上图拆散一个电子对(库珀对)产生两个单电子至少需要能隙宽度2Δ的能量。
热运动可以拆散电子对产生单电子。
能隙的存在使得在温度T 远低于临界温度Tc 时超导体中单电子(正常电子)的数目按exp-2Δ/kT 变化。
这就导致超导体的电子比热容和热导率按温度指数规律变化。
超导体基本原理:电阻为零的电流传导超导体是一种在低温下表现出电阻为零的物质。
以下是超导体的基本原理:1. 零电阻:超导现象:超导是一种在超导体材料中观察到的现象,其最显著的特征是在超导态时电阻为零。
临界温度:超导体表现出超导性的温度被称为临界温度(Tc)。
通常,超导体在低于临界温度时才会表现出零电阻的特性。
2. 迈克耳孙-莫里斯效应:电子对结合:这一效应的基础是库珀对的形成。
在低温下,电子之间通过声子相互作用形成库珀对。
零电阻机制:库珀对能够以一种协同的方式通过晶格而无碰撞地运动,导致电阻的消失。
3. 迈斯纳效应:磁场排斥:超导体在超导态时会排斥磁场,这被称为迈斯纳效应。
Meissner效应:当磁场穿过超导体时,它会被完全排除,使超导体内部不受外部磁场的影响。
4. 类型I和类型II超导体:类型I:具有清晰的临界温度和完全迈斯纳效应,如铅和汞。
类型II:在高磁场下仍保持超导性,表现出混合态,如铌和锆。
5. BCS理论:电子对结合:费曼、库珀和施里弗提出的BCS理论解释了超导现象,主张电子通过声子相互作用形成配对。
BCS波函数: BCS波函数描述了超导体中电子对的状态,它们以库珀对的形式出现。
6. 应用:磁共振成像(MRI):超导体广泛用于MRI设备,利用超导磁体产生高强度磁场。
磁悬浮列车:超导磁体用于磁悬浮系统,使列车在悬浮状态下运行。
能量传输:超导体在能量传输和存储方面有潜在应用,例如超导电缆和超导磁体储能系统。
总体而言,超导体的基本原理涉及电子形成库珀对,并通过声子相互作用实现零电阻。
超导体在科学和技术领域中的应用不断拓展,为许多领域带来了创新和进步。
超导体电阻率摘要:一、超导体电阻率的概念1.电阻率的定义2.超导体与普通导体的区别二、超导体电阻率的特性1.零电阻特性2.高温超导体的电阻率三、影响超导体电阻率的因素1.温度2.磁场3.化学成分和结构四、超导体电阻率的应用1.能源传输2.磁浮技术3.量子计算正文:超导体电阻率是指在超导状态下,导体的电阻程度。
电阻率是描述材料导电性能的物理量,通常用符号ρ表示,单位是欧姆·米(Ω·m)。
在超导状态下,超导体电阻率具有独特的特性,使其在许多领域具有广泛的应用。
超导体电阻率的核心特性是零电阻特性。
在超导态下,超导体内部的电阻为零,电流可以在其内部自由流动。
这一特性使得超导体在能源传输、磁浮技术和量子计算等领域具有巨大的潜力。
然而,要实现超导状态,需要将超导体冷却到临界温度以下。
近年来,高温超导体的研究取得了突破,使得超导技术在室温下应用成为可能。
超导体电阻率受多种因素影响。
首先是温度,超导体的电阻率随着温度的升高而增加。
高温超导体虽然不能实现室温下的超导,但其相对较高的临界温度已经使得它们在实际应用中具有很大的优势。
其次是磁场,超导体在磁场作用下会出现磁通拥堵现象,导致电阻率增加。
最后是化学成分和结构,不同的材料和结构对超导体电阻率有重要影响。
在能源传输领域,超导体电阻率的特性使得电力传输过程中的能量损耗大大降低,提高了能源利用效率。
在磁浮技术领域,超导体可以产生强大的磁场,使磁浮列车在轨道上悬浮,减少运行阻力,提高运行速度。
在量子计算领域,超导体的零电阻特性为实现量子计算提供了可能。
总之,超导体电阻率的研究对于推动超导技术的发展具有重要意义。