3 超导体微观理论
- 格式:doc
- 大小:306.50 KB
- 文档页数:9





第七章超导的微观理论模型——BCS理论§1建立BCS理论的实验基础§2Fröhlich模型:简化电声子相互作用模型§3 屏蔽库仑作用§4造成电子间相互吸引的电—声子相互作用是有条件的§5Cooper对§1 建立BCS理论的实验基础1.1 超导相变是电子态相变实验表明超导相变不影响晶格点阵的结构和振动。
揭示了超导相变是电子态相变。
但这并不表示超导相变与晶体点阵结构和振动无关。
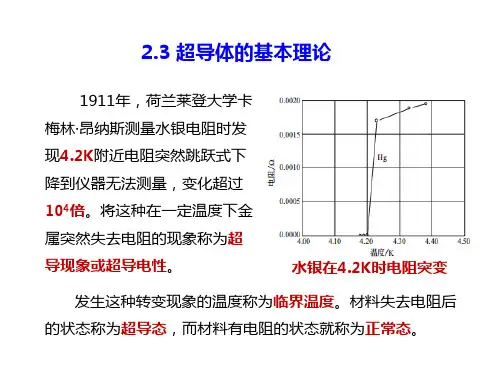
所用实验:x射线衍射,中子散射,穆斯堡尔谱3)/(3c T T TTce50.117.9−C e s /γT c=c es T C γ/T c /T单电子体系很类似,从而揭示超导态存在能隙。
2)远红外吸收z当频率ν< νg,远红外光经多次反射后到达碳电阻,由于超导壁不吸收能量,碳电阻收到大的辐射,碳电阻有一个阻值;z当ν≥νg,超导壁大量吸收能量,碳电阻收到的辐射小,阻值变化。
ω==Δ2z超导能隙:发生超导转变是由于超导电子凝聚到一个能隙以下,体系能量降低;而且这些电子是长程有序的(宏观量子效应,Pippard相干长度),可见电子之间必然存在相互作用。
z一般认为,电子之间存在库仑排斥作用,不能导致体系能量的降低。
只有电子之间存在相互吸引才能导致体系能量的降低。
z能隙的存在表示要使一个电子跳过能隙,必须拆散电子之间的吸引作用,因此,能隙是由于电子间的相互吸引作用而造成的。
z电子间是如何相互吸引的??传导电子行为有重要影响。
§2 Fröhlich模型:简化电声子相互作用模型Frohlich模型112电子—声子相互作用能把两个电子耦合在一起,这种耦合就好象两个电子之间有相互吸引作用一样。
§3 屏蔽库仑作用z电中性:金属内电子、离子之间的作用基本上是静电库仑力,电子气体的密度在宏观上是均匀的,体系的正、负电荷密度是相等的。
z库仑斥力:倾向于排斥其它电子,在某个电荷周围的负电荷密度低于平均值,如果跟踪观察这一个电子,则这个电子的负电荷的库仑场受到裹着它的等效正电荷的屏蔽。




超导现象的巨观和微观理论解释超导是物理学中一种引人注目的现象,指的是一些物质在低温下表现出完全无电阻的特性。
超导现象的原理一直是科学家们研究的焦点之一,对于揭示其微观机制和应用于实际中具有重要意义。
本文将从巨观和微观两个层面探讨超导现象的理论解释。
首先,我们从巨观层面入手,观察超导现象的整体特性和性质。
当某些物质被冷却到一个临界温度以下时,就会出现超导现象。
在超导状态下,电流可以无损耗地在材料内部流动,这意味着电流可以在超导体内无限延续下去而不会受到阻力。
这种特性使得超导材料在电力输送、电子器件制造等领域具有广泛的应用潜力。
对于超导现象的巨观解释,目前最被广泛接受的理论是BCS理论,即“巴丁-库珀-斯坦因理论”。
BCS理论认为,超导是由于电子与晶格振动之间的相互作用导致的。
在低温下,晶格振动会形成一种被称为“库珀对”的特殊态,电子通过与这些库珀对的相互作用而形成一个整体,从而形成了超导现象。
BCS理论的核心是超导能隙的形成。
超导能隙是指在超导体中,电子必须具有一定的能量以克服超导材料产生的能隙才能从一个能级跃迁到另一个能级。
这就是为何只有在低温下才能观察到超导现象。
超导能隙的形成和库珀对的形成密切相关,库珀对提供了足够的能量使电子跃迁,进而产生超导现象。
接下来,我们来探讨超导现象的微观解释。
超导的微观机制可以从电子的运动和相互作用的角度进行解释。
在超导材料中,电子之间存在相互排斥的库伦力,这会导致电子在晶格中受到散射,并且能量会损失到晶格中去。
然而,在低温下,电子与晶格振动的相互作用会导致电子和晶格之间的相互作用具有吸引力,形成库珀对。
库珀对的形成是超导现象的关键步骤。
正常情况下,库伦排斥力会使得电子间的相互作用能增加,从而阻碍超导的发生。
但在超导材料中,晶体格子振动引起的吸引力抵消了库伦排斥力,形成了库珀对。
这种库珀对是由电子和晶格共同参与的量子态,具有特殊的运动和相互作用方式。
库珀对的产生降低了电子之间的相互作用能,使得电子可以在超导材料中自由地流动而不受到散射的干扰。

超导体的理论和实验研究超导体是一种在极低温度下表现出零电阻电流通能力的物质,它是现代物理学和工程学的重要研究领域之一,因为它的性质与许多应用有关,包括能源传输、电子设备和磁共振成像等。
本文将介绍超导体的理论和实验研究,以及这些研究在实际应用中的潜力。
超导体理论超导体理论的起始点可以追溯到1911年,尤金·恩斯特·哈赛和海因里希·卡鲁伊斯提出了超导现象的解释。
他们认为,超导电性是由电子对形成引发的,即两个电子成对地在晶格中移动,因而形成一种无阻包络态。
但这个理论并没有解释出超导临界温度,此后研究者又提出BSC理论,它认为,超导电性是由电子间的库伦吸引力所产生的,而这种吸引力只能在低温高纯度状态下才会出现,所以超导材料的温度低于某一临界温度时才会产生超导电性。
超导体实验研究实验研究是超导体研究的基础,它可以有效地验证超导体理论的正确性,也可以为实际应用提供足够的实验数据。
首先来介绍超导材料的制备和检测。
超导体的制备是非常复杂和耗费成本的过程,需要满足极低温,高压、高纯等条件。
从材料的制造、约束、代码阐明到实验室的构建,一切都要精准计算,才能达到预期效果。
接下来是超导体的性质研究。
超导体的理论基础是复杂的。
但超导体性能随温度变化的关系是最为重要的研究。
在超导温度下,超导体会出现零电阻的特点,并且磁场作用下失超导的超导样品的磁滞现象是研究者们经常利用的工具。
越来越多的实验研究表明,超导材料中的单粒子和两个粒子最为关键,如何控制和制备这些粒子是解决超导体研究的核心问题之一。
另外,也需要充分调查超导体的微观特性和相变行为。
超导体在实际应用中的潜力超导体理论和实验研究的深入,进一步推动了超导体在实际应用中的各种可能性。
一方面,超导体的零电阻特性可以用于构建大功率电缆和稳定的电源,有效提高了能源传输的效率和可靠性。
另一方面,超导体的磁性和巨磁效应在医学和物理学中具有广泛的应用。
如磁共振成像技术已经成为现代医学诊断中的重要手段。
超导相变机理的微观理论超导现象是固体物理学中的重要现象之一,其具有高电导、零电阻和磁场排斥等特点,对能源传输、电子器件等领域具有广泛的应用前景。
超导材料在低温下显示出这些独特的性质,但其具体的相变机理却一直以来都是科学家们研究的焦点。
本文将就超导相变机理的微观理论进行论述。
1. 超导材料的基本特性超导材料是指在低温下,电阻突然减为零的材料。
其超导特性可分为两类:一类是Type-I超导体,磁场在超导转变温度下完全被排斥出材料;另一类是Type-II超导体,磁场在临界磁场下进入材料形成磁通线,但电流仍然无阻碍地通过。
这些特性相信与材料电子结构和能带的相关信息密切相关。
2. 超导相变的微观理论在材料研究中,研究者首先发现,绝大部分超导体的超导转变与电子对(Cooper pair)的形成和破裂有关。
Cooper pair是一对电子,在晶体中通过库伦相互作用形成一对具有相反自旋的束缚态。
当材料处于超导态时,Cooper pair的形成能量下降,对电子的相互作用强化使得这对电子对能够通过晶格存在较长的寿命。
基于BCS理论,Bardeen、Cooper和Schrieffer提出了描述超导相变的微观理论,BCS理论。
该理论认为超导的本质是电子-晶格的相互作用引发的电子对_condensate_相变。
其关键观点包括:电子在晶格振动场中发生配对(Cooper pair);电子对具有玻色性质,可与振动的晶格模式相互作用;当温度降低到临界临界温度时,超导态形成并且电子对开始在晶格中运动。
3. BCS理论的关键步骤BCS理论中描述了电子配对的形成和超导相变的关键步骤。
总结起来,主要包括以下几个方面:a. 电子与晶格的相互作用:晶格振动产生了电子间的吸引力,这种吸引力可以被看作是一个传递相互作用,即库伦相互作用。
b. Cooper pair的形成:在超导转变温度以下,传导带上电子和费米能级以下的能量态可以形成状态密度较高的电子对,而这些电子对被称为Cooper pair。
神奇的超导:超导理论的发展超导理论的发展超导现象被发现以后,许多理论物理学家试图对超导的起源进行理论上的描述。
然而,超导微观机理的建立经历了一个艰巨而曲折的漫长过程。
20世纪初期,许多顶级的理论物理学家都试图从量子力学基础上理解超导电性,但最终并没有获得成功,其中包括爱因斯坦,玻尔,海森伯,费曼等。
直到超导发现近50年后,超导微观理论才被建立。
图3.第一类超导体和第二类超导体的磁场-温度相图在最初对超导电性的认识过程中,唯象理论起到了非常重要的作用,如二流体模型和伦敦(London)方程等。
其中最著名的是前苏联物理学家金茨堡(Ginzburg)和朗道(Landau)于1950年建立的金茨堡-朗道理论(简称G-L理论),他们从热力学统计物理角度描述了超导相变。
G-L理论以朗道的二级相变理论为基础,假设了超导态和正常态之间的相变可以用一个所谓相变序参量来描述,从而推导出超导转变附近的临界行为。
G-L理论告诉我们,外磁场并不是完全不可以进入超导体,实际上它穿透进入了超导体的表面。
即使在超导临界温度以下,如果外磁场足够强,那么它也可以完全进入超导体而彻底破坏超导态,即恢复到正常态。
能够破坏超导态的磁场称为临界场Hc,一些超导体只存在一个临界场,称为第一类超导体。
而实际上大部分超导体存在两个临界场,即下临界场Hc1和上临界场Hc2,这些超导体被称为第二类超导体(图3)。
当磁场增加到下临界场时,磁场将进入超导体内部,完全抗磁性被破坏,但是超导电子对仍然以超导环流的形式存在,零电阻态还被保持,这个中间状态被称为混合态;当磁场进一步增强到上临界场时,零电阻态也被彻底破坏,超导体恢复到有电阻的正常态。
1957年,阿布里科索夫(Abrikosov)从G-L方程导出,在第二类超导体中,磁场其实是以量子化的量子磁通涡旋进入超导体内部的,一个磁通量子为Φ0 = h/2e(约为2.067×10-15Wb)。
在低温和低场下,量子磁通涡旋将有序地排列,如图4所示。
第四章超导电性微观理论BCS (J. Bardeen, L. N. Cooper, J. R. Schrieffer)1923-1927年量子力学建立后,被迅速应用到实际中,解决了许多问题,获得了巨大的成功F. Bloch将量子力学运用到单电子模型上,很好地解释了正常金属的导电性质,但不能解释超导电性现象原因:Bloch理论中忽略了某种相互作用,而这种作用对超导电性是重要的库仑相互作用,自旋-自旋相互作用,磁相互作用,电子-晶格相互作用1947年Heisenberg-Koppe库仑作用是导致超导电性的原因这一理论受到了很多批评F. London:同意库仑作用是导致超导电性的主因,但认为超导电性是一种动量空间中的凝聚,而非Heisenberg理论中普通空间中的电子格子的有序态。
Shoenberg:这个理论的唯一价值在于它活跃了关于超导问题的讨论不能解释为什么电子格子与正常电子的碰撞无能量损失这个理论中的凝聚态无超导性质J. M. Schafroth, S. T. Butler, J. M. Blatt玻色---爱因斯坦凝聚“在没有外场时,任何电子系统的最稳定的状态是没有电流的状态”F. Bloch 的两个论断“任何超导理论都是可以反驳的”1950 Fröhlich理论上证明电一声相互作用可以导致电子间的吸引1956-1957 BCS (J. Bardeen, L. N. Cooper, J. R. Schrieffer)Cooper 电子对试探波函数突破1950 Maxwell ReynoldsT c M 1/2=常数BCS (J. Bardeen, L. N. Cooper, J. R. Schrieffer)4.1 主要实验事实①晶体结构在超导相变前后不变1924Keesom and Onnes, Pb XRD1955Wilkinson, Pb 和Nb 的中子散射1962Wiedemann ,Mössbauer Sn Θ不变超导转变和晶格无关,电子态的相变T bT c es c e T C /−=αγ 1.5b 2≈=c g bkT E 1951 Goodman1954 Corak ②超导能隙电子比热远红外吸收eVeVEg 0.1m~10~ 4−⇒超导电子的激发能谱上有能隙-5g 10~/E E 10~F F eV E 能隙非常小,导致能隙产生的作用一定非常微弱,比库仑作用要弱得多,找不出产生微弱的吸引作用的任何明显的机制,这在一个时期内曾是建立任何超导微观理论的障碍!③同位素效应1950 Maxwell Hg Reynolds T c M 1/2=常数qc MT ω~~2/1−零电阻迈斯纳效应T=T c 比热跳跃二级相变相干长度,非局域效应正常区一超导区的界面能(I 类超导体)超导电子更有序,且长程序尽管超导转变前后晶格本身没有变化,但晶格振动在电子态相变(超导)中有重要作用。
超导体的微观机理与唯象理论的研究引言:超导体是一种在低温下表现出无电阻电流传导现象的材料。
它具有重要的理论和实际应用价值,例如在能源传输、磁共振成像、电子器件等方面都有广泛的应用。
本文将重点讨论超导体的微观机理与唯象理论的研究,包括超导现象的物理定律、实验准备和过程,并探讨其在其他专业性角度的应用。
一、超导现象的物理定律1. 超导的临界温度:根据超导现象的临界温度,超导体可以分为低温超导体和高温超导体。
对于低温超导体,其临界温度通常在几开尔文以下。
根据BCS理论,低温超导体的超导性来源于库伦相互作用引起的电子配对。
而对于高温超导体来说,其临界温度可以达到液氮的沸点(77K),并且不需要太强的电子-电子相互作用即可形成电子配对。
2. 零电阻电流:超导体在超导态时的最显著特征之一是零电阻电流,即电流可以在超导体内部无阻抗地流动,这是超导现象的本质特征之一。
这是由于电子配对导致的库伦相互作用减弱了散射过程,电流的传输不会受到电阻的限制。
3. 磁场抗拒现象:超导体在零阻态下对外界磁场表现出完全的抗拒,这被称为迈斯纳效应。
根据迈斯纳效应,当磁场越过超导体表面时,在超导体内部会形成一个抵消外磁场的屏蔽区域,使得磁场无法渗入超导体内部。
二、实验准备和过程1. 实验器材:进行超导体的微观机理研究需要一系列实验器材,包括低温制冷设备、电磁炉、氦气瓶、超导体样品等。
低温制冷设备用于将超导体冷却到其临界温度以下,以观察超导现象的发生。
电磁炉用于加热样品,以探索高温超导体的特性。
而氦气瓶则用于提供低温制冷所需的液氦。
2. 实验过程:在实验过程中,首先需要选择合适的超导体样品,并使用低温制冷设备将其冷却到超导态的临界温度以下。
然后,通过电磁炉进行加热实验,观察高温超导体的临界温度和其他性质。
实验过程中需要测量电阻、磁场、电压等参数,以获得相关的物理数据和曲线。
三、应用和其他专业性角度1. 超导磁体:超导磁体是应用超导体材料制造的磁体器件,具有巨大的磁场强度和高能效的特点。
物理学中的超导体理论与实验研究超导体是指在低温下电阻为零的一类物质。
这个现象在 1911 年被荷兰物理学家哈特霍恩首次观测到,此后,超导体的研究一直是物理学界的热门课题。
超导体具有多种特殊的性质,例如磁场排斥性、电场屏蔽性和零电阻性,因此在工业、医学、基础科学等领域都有广泛的应用。
本文将介绍超导体的基本理论,主要实验方法和应用前景。
1. 超导体的基本理论超导体的零电阻状态表明电子在超导体内运动没有电阻。
这一现象的发生是由相变引起的。
在超导体内,电子形成一对形成“库珀对”的束缚态。
当超导体温度降到一个临界值以下时,电子态的分布开始发生变化,电子越来越倾向于组成“库珀对”,从而导致电阻以指数级别下降,最终归为零。
超导体的临界温度是其研究中的重要参数,这个值通常低于 20 K。
许多超导体材料的临界温度在 40 K 以上,其中最先发现超导现象的汞(Hg)元素的临界温度就很低,只有 4.2 K。
超导体的临界温度取决于多种因素,包括压力、纯度和晶格结构等。
研究者们通过对各种材料的实验探究,得到了关于超导体物理性质的深入认知。
除了这一基本理论之外,还有一些关于超导现象背后的理论推导。
这个领域的出现始于 1957 年,当时美国物理学家巴丹和柯普考虑到了超导现象的量子性质,提出了一个与此相关的统一理论。
这被称为 BCS 理论,其全称是巴丹、柯普和斯奈尔的缩写。
BCS理论解释了为什么电子会形成“库珀对”,从而更深入地理解了超导现象。
他们还提出了一个重要的概念——超导能隙。
这是一种特殊的能量状态,与库珀对从非发散态能量状态到发散态能量状态的能量差感应相同。
在聚变等一系列物理实验中,用超导体来制造高强度的磁场,磁体中的超导体形成了约束电流的强大磁场。
然而,BCS 理论不适用于高温超导体,这些超导体的临界温度远高于其它材料。
2. 超导体的主要实验方法超导体研究中常用的主要实验方法是电阻测量和磁性测量。
电阻测量是超导体的零电阻状态的识别方法,通过测量电流和电压来确定电阻。
3超导体微观理论超导微观机制经典理论对超导电性产生的原因无法解释。
在量子论建立不久,F.伦敦就指出,超导环内的磁通是量子化的。
因此,超导电性是宏观世界的量子现象。
1962年,实验证实磁通是量子化的。
同位素效应所谓同位素效应是指超导体的临界温度依赖于同位素质量的现象。
1950年英国H.弗罗利希指出,金属中电子通过交换声子(点阵振动)可以产生吸引作用。
他预言超导体的临界温度与同位素的质量之间存在一定的关系。
所谓“临界温度”,就是导体从正常导电状态变为超导电状态时的转变温度。
果然,弗罗里希的预言得到了实验的证实。
1950年麦克斯韦(E.Maxwell )和雷诺(C.A.Rayhold )各自独立圣测量了水银同位素的临界转变温度。
实验发现:T C ∝М-1/2,其中М为同位素质量。
同位素效应把晶格振动(其量子称为声子)与电子联系起来了,它告诉人们电子-声子的相互作用与超导电性密切相关。
弗罗利希经过分析后认为,同位素之间的电子分布状态是相同的,而原子质量是不同的,那么,超导电性会不会与晶格原子的性质有关呢?也许,超导的出现(即电阻的消失)是由于电子和晶格原子的相互作用才产生的吧!那么,电子和晶格原子是怎样互相作用的呢?弗超导能隙(energy gap of superconductors )实验证明,超导态的电子能谱与正常态不同,在费密能E F (最低激发态与基态之间)附近出现了一个半宽度为Δ能量间隙。
Δ≈10-3~10-4eV 。
如上图拆散一个电子对(库珀对)产生两个单电子至少需要能隙宽度2Δ的能量。
热运动可以拆散电子对产生单电子。
能隙的存在使得在温度T 远低于临界温度T c 时,超导体中单电子(正常电子)的数目按exp(-2Δ/kT)变化。
这就导致超导体的电子比热容和热导率按温度指数规律变化。
当电磁波(微波或远红外线)的频率足够高(h ν≥2Δ)时,同样可以激发出单电子。
此时超导体会强烈地吸收电磁波。
在以超导体为一个电极的隧道结中,当结电压足够高(V ≥Δ/e)时,大量的电子对被拆散,形成单电子参与隧道过程,使隧道电流在V=Δ/e处突然上升,若隧道结的两个电极都是超导体,能隙为Δ1、Δ2,则在V =(Δ1+Δ2)/e处突然上升。
这些现象都证明能隙的存在,并可用来测定能隙值2Δ。
库珀电子对1956年,L.N.库珀(L.N.Cooper )从理论上证明了费密面附近的两个电子,只要存在净的吸引作用,不管多么微弱,都可以形成束缚态──库珀对。
库珀发现,如果带电粒子的正则动量(机械运动与场动量之间之和等于零,那么很容易从超导电流密度的基本关系:J s =-ns e*υs 得到伦敦方程。
可见超导态是由正则动量为零的超导电子组成的,它是动量空间的凝聚现象。
相干长度:1953年,皮帕德(A.B.Pippard )证明,当一个电子从金属的正常区移动到2′超导区时,其波函数不能从它的正常态值突然转变为超导态的值,这种转变只能发生在一个距离ξ上,ξ被称为相干长度。
相干长度和穿透深度是表征超导体的基本参数。
形成库珀电子对的最佳方式是动量相反时自旋相反的两个电子组成。
BCS理论1956年,L.N.库珀从理论上证明了费密面附近的两个电子,只要存在净的吸引作用,不管多么微弱,都可以形成束缚态──库珀对。
第二年,J.巴丁、库珀和J.R.施里弗建立了完整的超导微观理论(BCS理论)。
BCS理论是以电子-声子相互作用为基础解释超导电性的经典理论,它能很好地解释金属元素及金属间化合物的超导电性。
BCS理论是以近自由电子模型为基础,是在电子-声子作用很弱的前提下建立起来的理论。
对于某些超导体,例如汞和铅,有一些现象不能用它来解释。
在BCS理论的基础上发展起来的超导强耦合理论,对这些现象能很好地解释(见强耦合超导体)。
两个基本概念。
第一,超导电性的起因是费密面附近的电子之间存在通过交换声子而发生的吸引作用。
第二,由于这种吸引作用,费密面附近的电子两两结合成对,叫做库珀对。
关于通过交换声子而发生的吸收作用,可以按如下的图像来理解。
一个电子状态发生变化,能量和动量从ε1、p1变为ε1′、p1′。
这个状态的改变引起了固体中整个电子气电荷分布的扰动。
这种扰动必然牵动点阵振动,即发射声子。
点阵振动反过来也可以影响电子气。
影响的结果可以使电子气复原,能量和动量为ε1′、p1′的电子恢复到原来的状态ε1、p1,其效果就是电子在运动过程因牵动点阵而增加了惯性,或有效质量。
影响的结果也可以是使另一个电子发生状态的变化,从ε2、p2变为ε2′、p2′,这就是声子被另一个电子吸收。
后一种情形的结果是一对电子之间发生了能量和动量的交换,也就是发生了以声子为媒介的电子间的间接的相互作用。
计算表明,当每一个电子前后状态的能量差小于声子的能量时(按测不准关系,不要求中间过渡的声子服从能量守恒),这种相互作用是吸引的。
考虑到费密面以下几乎都是被占据了的状态,以及量子力学的泡利不相容原理,可知只有在费密面附近的电子之间才存在吸引作用。
这一部分恰恰也就是呈现超导电性的电子。
吸引作用的强弱,取决于一对电子(ε1、p1)、(ε2、p2)可能转变过去的状态(ε1′、p1′)(ε2′、p2′)的多寡。
据此可知,在费密面附近动量相反、自旋也相反的一对电子(p1=p↑,p2=p↓ε1≈ε2≈εF,)之间,存在比其他情形都要强得多的吸引作用。
假如这种吸引作用超过了两个电子之间的静电斥力,就会使一对(p↑,-p↓)的电子结合成库珀对,因为这会使电子气的能量下降到低于正常费密分布时的能量。
费密面附近的电子两两结合成对,改变了这些电子的能谱。
使得在连续的能带态以下,出现一个单独的能级,即结合成对的状态。
单独能级与连续能级之间的间隔为Δ,叫做超导体的能隙。
把一个电子对拆成不相关的两个单独电子,至少要给予一定的能量,这个能量就叫结合能,其值为2Δ,即至少要给予每个电子以能量Δ。
因为拆开之后,两个电子不成为库珀对,每个电子都处在连续能级的状态上。
计算表明,能谱的连续部分的结构也发生了变化,能量值不是正常金属情形的ε而是。
另外,各种大小能量的状态数目也和正常情形下不同。
因吸引作用而结合起来的库珀对,类似于一个电子和一个质子组成的氢原子这样的体系,但又有很大的差异。
用测不准关系可以估计出一个库珀对中电子间的距离大约是10μ米,即大约是点阵常数的104倍。
所以库珀对是一个很松弛的体系。
事实上,它的结合能2Δ也极小,一般只有10-3eV的数量级。
因此,库珀对其实不过是运动发生密切关联的一对电子,不像氢原子可以整体地当作一个粒子。
必须强调,吸引作用、库珀对和能隙,都是电子气的集体效应。
如上所述,一对电子(p ↑,-p↓)间吸引作用的强弱, 取决于允许它们转变过去的状态(p↑,-p↓)的多寡。
假如在费密面附近存在一些未成对的电子(p1↑,-p2↓)等等, 由于泡利不相容原理禁止电子对(p↑,-p↓)转变到状态(p1↑,-p1↓)、(p2↑,-p2↓)等等去,因而就会减弱电子对(p ↑,-p↓)间的吸引。
这样,一个电子对内部的吸引强弱,电子对结合能或能隙Δ的大小取决于费密面附近全部电子的状态分布。
当费密面附近电子全都两两结合成对时,Δ最大。
拆散一些库珀对,则剩下的每个库珀对的结合也变得更加松弛。
因此,全体库珀对组成一个凝聚体,它构成二流体模型的超流成分(超导电性)。
凝聚体的各个库珀对协同地或相干地处在有序化状态。
能隙Δ便是有序化程度的量度。
所以Δ的更基本的意义是序参量。
这种有序化造成规范对称性的自发破缺,结果,所有的库珀对,可以是每个对的总动量一致为零(无电流态),也可以是每个对的总动量一致地等于某个非零数值(无电阻地传输电流,即超流动态)。
在绝对零度,费密面附近的电子全都两两地结合成库珀对,这时序参量Δ为最大。
当温度高于绝对零度时,由于热激发,一些库珀对被拆散成单个电子,能隙或序参量也减小。
当到某个温度Tc时,库珀对全被拆散,Δ变为零,超导态消失而转入正常态。
Tc就是超导体的临界温度。
因此,超导-正常相变是二级的。
超导隧道效应正常隧道效应两金属或金属和超导体或两超导体之间有一薄绝缘层的结构称为隧道结。
贾埃弗超导金属结I—V曲线I1221超导体1一侧能隙以上的正常电子可以隧穿到超导体2一侧形成小的隧道电流,显然随着eV 的增加,将更多的这种电子通过隧道效应而达到超导体2中去,故起始电流上升。
当V=(Δ2-Δ1)/e 时,达到极大值。
V 继续增加在超导体1一侧能隙以上的正常电子所面对的超导体2中的空态密度变小,故隧道电流下降,持续到V>(Δ2+Δ1)/e 时,在超导体1一侧能隙以下的电子开始面对超导体2一侧能隙以上的大量空态,因超导金属结I —V 曲线E F2 E F2E F2 I E约瑟夫森效应(Josephson effect)当绝缘层的厚度只有几十埃时,B.D.约瑟夫森预言,电子对可以越过绝缘层形成电流,而隧道结两端没有电压,即绝缘层也成了超导体。
电子对通过两块超导金属间的薄绝缘层(厚度约为10埃)时发生的量子力学隧道效应。
1962年,英国牛津大学研究生B.D.约瑟夫森首先从理论上对超导电子对的隧道效应作了预言,不久就为P.W.安德森和J.M.罗厄耳的实验观测所证实。
十多年来,它已在超导电性的研究领域内逐渐发展成为一个新的重要分支──约瑟夫森效应和超导结电子学。
直流约瑟夫森效应当直流电流通过超导隧道结时,只要电流值低于某一临界电流I c,则与一块超导体相似,结上不存在任何电压,即流过结的是超导电流。
但一旦超过临界电流值,结上即出现一个有限的电压,结的性状过渡到正常电子的隧道特性。
图1 Sn-SnOx-Sn结构的电流和电压关系临界电流一般在几十微安到几十毫安之间。
超导隧道结的临界电流对于外加磁场十分敏感。
不是外加磁场的单调函数,而是随着外磁场的增高,呈现如图2 Sn-SnO x-Sn结的约瑟夫森电流和磁场的关系所示的周期性变化,类似于光学中的夫琅和费衍射图样。
相邻两最小值之间的磁场间隔H0与结面积的乘积正好等于一个磁通量子,即韦伯。
交流约瑟夫森效应如果在超导结的结区两端加上一直流电压V(当然,这时电流大于临界电流),在结区就出现高频的超导正弦波电流,其频率与所施加的直流电压成正比,有如下关系式或,比例常数2e/h=483.6×106Hz/μV。
这时,结区以同样的频率(若所加电压是几微伏,则在微波区域;若为几毫伏,则在远红外波段)向外辐射电磁波。
超导隧道结这种能在直流电压作用下,产生超导交流电流,从而能辐射电磁波的特性,称为交流约瑟夫森效应。
如果用频率为的微波辐照约瑟夫森结,当时,外加微波和结辐射的电磁波发生共振,则在I-V特性上可以测到恒压电流,随着n=0,1,2,…, 在I-V特性上出现阶梯效应,如下图3Sn-SnO x-Sn结的直流常电压-电流阶梯所示。