超导电性理论

超导电性理论研究及其在电力输送中的应用超导技术是一种具有许多优势的电学技术，如低能量消耗、高电流密度和高能量效率等。

因此，它可以被广泛应用于电力输送和能量存储等领域。

在本篇文章中，我们将介绍超导电性的基本原理和超导材料的种类，以及超导技术在电力输送中的应用。

一、超导电性的基本原理超导电性是电学理论中的一种现象，是指在一定条件下，某些材料在经历过冷冻等处理后，就会失去内部电阻，电流可以在其中自由流动。

从物理学的角度来说，超导电性是一种电子对在材料中导电过程的一种具有独特物理性质的特殊形态。

具有超导电性的材料被称为超导体，具有超导电性的超导体被称为超导体。

当一个电流通过一个超导体时，它不会遇到任何的电阻。

这意味着，电流可以在超导体内无限流动，如果电流源并不受到限制，则意味着能够产生相当高的电流强度。

这是因为，当一个电流通过一个超导体时，电子呈现出一种独立配对的现象，这种独立配对现象可以抵消电子间相互排斥的作用力，使得电子自由流动。

二、超导材料的种类超导体是具有无电阻电流输运特性的材料。

超导材料广泛存在于自然界中，例如铜氧化物、铀钿合金等。

在工业中，常用的是低温超导体和高温超导体。

低温超导体具有比较高的超导临界温度，这种温度在接近绝对零度时开始显示。

在我们的日常生活中，使用温度比较低的液氦可以制冷低温超导体。

高温超导体是指在高于液氮的温度下显示超导性质的材料。

这种材料呈现出比低温材料更高的超导温度。

三、超导技术在电力输送中的应用电力输送通常通过导线传送电能，由于各种因素的影响，如电阻、电感、电容以及电磁干扰等，导致电能损耗。

超导技术可以解决这些问题，因为它提供了一种能够产生高电流密度并且无电阻的电流传输方式。

在电力输送中，超导技术有许多优点，例如有效降低能量损耗、提高电流密度、减少输电系统的大小、提高电力质量，缩短电路响应时间等。

从经济效益和环境保护的角度进行考虑，超导输电系统将是未来电力输送的主要方向之一。

超导电性的原理和应用超导电性是一种在特定物理条件下出现的电性现象。

它表现为在超导态下，电流的阻力为零或接近于零。

超导电性的研究，既有基础科学意义，又具有重要的应用价值。

超导电性的原理超导电性的原理可以用BCS理论来解释。

BCS理论是由美国物理学家约翰-巴丁-肖克利、罗伯特-斯库兹和约翰-罗伯特-斯彭塞三人提出的。

他们发现，在某些材料中，当温度降低到一定程度时，电流的阻力会消失，这被称为超导电性。

在这种状态下，电子形成了一种称为“库珀对”的物质。

这些电子之间通过共振声子相互作用，形成了弱耦合。

这种弱耦合所产生的波动与聚集的电子相互反应，最终形成超导电性。

超导电性的应用超导电性有着广泛的应用。

其中最为重要的就是磁共振成像技术，它是获得人体内部结构影像的主要工具之一。

MRI机就是利用超导线圈制造高强磁场，使人体内部的原子顺应磁场方向排列，然后再加上一定的电磁波作用，使原子吸收和释放辐射能，通过分析此辐射能得到人体内部的影像。

超导电性还可应用于磁悬浮技术，即通过利用超导体的强磁场抵抗重力，使列车或车辆“飞”在导轨上，可以大幅提高列车的运行速度和安全性。

此外，超导电性还被广泛用于电力设备。

超导体可以制成超导电缆，它可以使电能传输损失降至极低，将来有可能取代铜线，成为传输电力的主要方式。

超导电性还可以用于制作超导电机和超导变压器等设备，可以使电力的输送效率和设备的安全性大幅提高。

超导电性的发现和研究，不仅填补了人类对电子性质的认识空白，也为人类创造出许多科技新突破。

在未来的发展中，超导电性还将在各个领域发挥积极的作用，为我们的生活和工作带来更多的创新。

超导电性的基本原理解析引言：超导电性是一种特殊的电性现象，指的是某些物质在低温下电阻突然消失的现象。

这一现象的发现和研究对于物理学的发展有着重要的意义。

本文将对超导电性的基本原理进行解析，从微观角度探讨超导电性的起源和机制。

第一部分：超导电性的发现超导电性的发现可以追溯到1911年，当时荷兰物理学家海克·卡末林发现在液氦的温度下，汞的电阻突然消失。

这一发现引起了科学界的广泛关注，并成为了一个重要的研究课题。

随后的几十年里，人们发现了越来越多的超导体，并研究了它们的性质和特点。

第二部分：超导电性的基本原理超导电性的基本原理可以通过两个重要的理论来解释：BCS理论和Ginzburg-Landau理论。

1. BCS理论BCS理论是由巴丁、库珀和施里弗三位科学家于1957年提出的，他们解释了超导电性的起源。

BCS理论认为，超导电性的产生是由于电子在晶格中形成了一种特殊的配对状态，即库珀对。

在超导体中，由于库珀对的存在，电子之间的相互作用减弱，电阻消失。

这种配对状态的形成是由于晶格振动引起的电子间的吸引力。

2. Ginzburg-Landau理论Ginzburg-Landau理论是由金兹堡和兰道于1950年提出的，它描述了超导体的宏观性质。

该理论认为，超导体在超导态下可以被看作一个宏观的量子态，具有宏观的量子相干性。

超导体的超导性可以通过一个宏观的波函数来描述，该波函数满足金兹堡-兰道方程。

根据该理论，超导体在外加磁场下会发生磁通量量子化现象，即磁通量只能取整数倍于基本磁通量的值。

第三部分：超导电性的应用超导电性的发现和研究不仅对物理学有着重要的意义，还在实际应用中发挥了重要作用。

1. 超导磁体超导磁体是超导电性的一种重要应用，它可以产生强大的磁场。

由于超导体在超导态下电阻为零，电流可以无损耗地流过，因此可以产生强大的磁场。

超导磁体广泛应用于核磁共振成像（MRI）、粒子加速器、磁悬浮列车等领域。

超导理论的基本原理超导理论是电学领域的一种前沿研究方向，是在特定条件下，某些材料在它们达到一定温度和适当的条件下表现出的“完美”的电性质。

有一些物质在温度降到某个非常低的水平时，电子的振荡被大大降低，电阻几乎为零，这种现象被称为超导现象。

超导现象被认为是目前电学领域最重要的现象之一。

超导理论的基础可以追溯到1933年，当时，荷兰物理学家Meissner和Ochsenfeld按照Langevin-Debye理论预测太阳黑子的磁场是和超导体内部的磁场互相排斥。

这种现象被称为Meissner 效应，Meissner效应是超导电性的一个基本现象。

超导电性的基本原理是由量子电动力学的图像导致的。

在量子电动力学理论中，电子是通过电磁场来传导电荷的。

超导电性的本质是电子和其它粒子的电动力学相互作用，而这种相互作用和电磁场中的粒子集团的作用有些类似，不同的是电子只能在超导物质中运动，而不是在真空中运动。

因此，超导电性是通过电荷的“集体运动”来实现的。

超导现象是一种冷态现象，需要将物质降温到低温状态才能实现。

实现这种低温状态的关键在于，要保持物质内部的热量尽可能少的流失。

为了实现这个目标，超导材料通常需要被置于低温环境中，比如在液氮中。

当材料被冷却到温度极低的时候，它的电性质会逐渐发生改变，电阻率会大幅降低，直至变为零。

超导物质所具有的特殊性质，是由于一种称为超导电子对的物质兴奋态在物质中存在的结果。

超导电子对可以看作是由两个电子组成的“卡希尔”（Cooper）气团。

卡希尔气团的形成发生在一定的温度和环境条件下，当卡希尔电子对穿过超导物质时，它们的能量可以一直被保持，直到限制它们移动的物理屏障出现。

这种现象最终导致了超导电性的出现。

超导电性的出现，是众多物理效应之一。

这种效应被广泛应用于工程领域，例如制造更快的计算机，更高效的电力转换器等等。

在现代科技发展过程中，超导电性扮演了非常重要的角色，也是未来科技发展的重要方向之一。

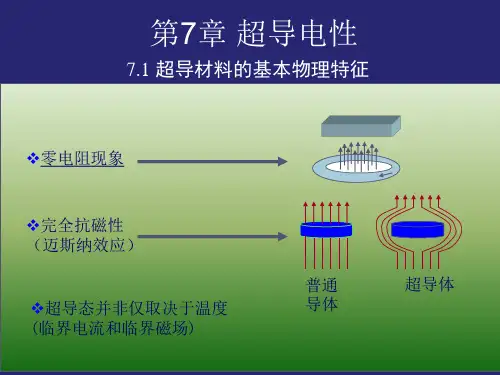
超导电性的微观机制及其应用超导现象是指某些物质在低温下表现出的零电阻和完全磁场排斥的特性。

这个神奇的现象在实际应用中具有广泛的潜力，例如超导电缆、磁悬浮列车和MRI设备等。

要理解超导现象的微观机制，我们需要了解它的起源和相关理论。

超导现象的理论基础是由约瑟夫·巴丁、约翰·巴丁和恩里科·费米等人在20世纪50年代初提出的。

他们基于费米-狄拉克统计原理和电子与晶格之间的相互作用来解释超导电性。

根据这个理论，当某些金属或合金被冷却到超导转变温度以下时，电子会以成对的方式聚集在一起形成所谓的库珀对。

这些电子通过库珀对与晶格振动相互作用，从而导致电阻为零。

在更详细的层面上，超导电性的理论可以用BCS理论来描述。

BCS 理论认为，超导电性是由于电子与晶格之间的相互作用导致了库珀对的形成。

在超导体中，晶格的振动形成了一种被称为声子的粒子，它们传递相互作用给电子。

这种相互作用使得电子能够成对出现，形成库珀对。

库珀对的形成使得电子能够在整个超导体中以一种协同的方式运动，从而导致零电阻和磁场的排斥。

超导现象的应用非常广泛。

其中一个最重要的应用是超导电缆。

超导电缆由超导体和包裹超导体的保护层构成。

由于超导体的零电阻特性，超导电缆可以输送大电流而无能量损耗。

这使得超导电缆在电力输送中具有巨大的潜力，可以实现更高效、更可靠的电力传输。

另一个重要的应用是磁悬浮技术。

通过在磁铁上放置超导体，可以实现磁悬浮效应。

超导体在低温下对磁场具有完全的排斥，因此可以使物体浮在磁场中。

这种技术在磁悬浮列车和磁浮风力发电等领域得到了广泛应用，可以实现高速、低能耗的运输和发电方式。

此外，超导体还被广泛应用于医学领域。

MRI（磁共振成像）是一种通过利用超导磁体产生强磁场的技术来观察人体内部结构的方法。

超导磁体能够提供非常强大的磁场，在医学图像诊断中起到关键的作用。

总之，超导电性的微观机制可以通过BCS理论解释。

超导现象具有零电阻和磁场排斥的特性，可以在超导电缆、磁悬浮技术和医学领域等多个应用中发挥作用。

超导电性的基本原理与研究进展超导电性是一种在极低温度下出现的特殊的电性现象，该现象在1908年被荷兰科学家海克·卡马林格首先发现。

超导材料的电阻为零，电流可以在其中自由地传导而不会损失能量，因此，在许多实际应用中具有广泛的应用前景，如磁悬浮列车、磁共振成像等领域。

本文将介绍超导电性的基本原理和发展历程以及最新的研究进展。

一、超导电性基本原理超导电性的基本原理在1928年由劳伦斯和奥森菲提出，即在超导材料中，电荷的运动可以与材料中的晶格振动形成一个密切的相互作用，引起电子的弛豫，并且导致它们集体地行动。

这种集体运动被称为库珀对，库珀对的产生也是超导电性的基本原理之一。

超导材料中，由于温度的降低，某些原子能够更紧密地接近，相互之间产生较强的吸引力，当电子和这些原子靠得足够近时，它们就会形成库珀对。

这些库珀对可以在超导材料中流动，创造一种电流传递的新途径，称为超导电流或Jeff Myron电流。

此外，超导电性还遵循BCS理论，即超导材料中存在着一种中介质，能够支持库珀对的稳定存在，这种中介质被称为费米液体。

BCS理论为解释超导电性提供了强大的理论支持。

二、超导电性的研究历程超导电性自第一次发现以来，吸引了许多科学家的关注。

1962年，JB Josephson发明了一种现象，称为Josephson效应，他发现在两个超导体之间存在电流可以自发地流动，而不受电场的作用，这种现象对现代电子学的发展产生了重大影响。

1986年，世界上第一个高温超导材料La2CuO4Ba4Y8O20被发现，它的超导温度达到了30K，相较于此前的超导材料，这个温度已经接近液氮的温度（即77K），因此形成了一股高温超导的热潮。

随着超导电性研究的深入，人们发现许多奇特的现象,如强磁场下的Meissner效应、超导电性与超流性的关系等，这些现象的发现深入了解了超导电性的基本特性，同时也启发了人们对超导材料的研究。

如今，人们对超导电性的理解和应用正在不断深化和拓展。

超导电性的原理及其应用前景超导电性是一种独特的物理现象，它指的是在低温下某些材料的电阻降至零。

这种现象被广泛应用于科学研究和技术领域，比如超导磁体、超导线材、超导电机等等。

本文将从超导电性的原理、实现方式以及应用前景三个方面来探讨这种神奇的物理现象。

一、超导电性的原理超导现象的发现可以追溯到1911年，当时荷兰物理学家海克·卡梅林根据麦克斯韦-波尔兹曼理论预测，在绝对零度下仍有可能存在一种几乎完美的电导体。

而这种理论预测，得益于量子力学的诞生，故称为BSC理论，其主要思想是在原子尺度上，电子之间存在弱吸引力，通过构成库珀对，从而体现超导电性。

具体来说，超导材料在低温下可以大量的生成非常强的库珀对。

这种特殊的电子对因为相互吸引而彼此结合在了一起，而且对于外部电场几乎没有任何反应。

当正常材料导电时，电子之间会受到杂质、晶格振动和外部电场的干扰，因此很难保持相互结合并且运动流畅。

而当超导材料降温到一定程度时，晶格振动会变得越来越弱，电子自然就更容易彼此结合，从而形成了高度协作的电流传输状态，引起了超导电性。

对于不同的超导体，其致超温度具有不同范围，自然也有非常不同的获得温度（温度越高，挑战也就越大），可以是近0K的低温超导材料，也可是30多度K 的高温超导材料。

二、超导电性的实现超导电性是非常神奇的物理现象，但它实际应用时需要做到一些技术性方案，才能达到预期的效果。

超导材料的制备、制冷技术的发展，都在推动着超导电性应用的不断扩大。

超导材料的制备是实现超导电性的一个关键点。

对于低温超导材料，目前主要制备方式是低温蒸发法，将合金加热到化合物体系的原始组成，然后对其进行某些处理以改善电性和超导性能。

对于高温超导材料，目前采用的是锰铝比例共沉淀法，或者提高煤质的盘状微晶法等。

制冷技术发展是实现超导电性的另一个重要方面。

低温超导材料需要使用液氦来冷却到极低的温度，而高温超导材料则可以使用制冷剂，如液氮。

超导电性的物理机制超导电性是指某些物质在低温下表现出的零电阻和完全磁通排斥的现象。

它被广泛应用于能源输送、磁共振成像以及粒子加速器等领域。

虽然超导电性已经被研究了数十年，但其物理机制迄今尚未完全揭示。

本文将探讨关于超导电性的物理机制的一些主要理论和实验发现。

超导电性的物理机制可以通过不同的理论框架进行解释。

最著名的是BCS理论和Ginzburg-Landau理论。

BCS理论由Bardeen、Cooper和Schrieffer于1957年提出，通过解释超导电性的微观机制而获得了诺贝尔物理学奖。

该理论基于电子和晶格的相互作用，在导体中形成库伦电子对。

这些库伦电子对被称为Cooper对。

库伦电子对的形成是由晶格中的振动引起的，这些振动被称为声子。

声子交换引起电子间的吸引力，促使电子形成Cooper对，从而导致超导电性的现象。

Ginzburg-Landau理论是对BCS理论的补充和扩展。

它是由Ginzburg和Landau于1950年代提出的，并在1962年Nobel物理学奖中被承认。

该理论通过引入一个宏观的量子场来描述超导态和正常态之间的相变。

该场被称为超导参量，它的非零值代表了超导态的存在。

Ginzburg-Landau理论还解释了超导电性的一些特征，如磁通的排斥。

实验观察不仅支持了BCS和Ginzburg-Landau理论，还揭示了其他有关超导电性的重要现像。

一个重要的实验现象是超导态与正常态之间存在一个临界温度。

在低于该温度的情况下，物质表现出超导电性，而在高于该温度时，物质表现出正常态。

这个临界温度被称为超导转变温度，通常用符号Tc来表示。

各种不同的材料具有不同的超导转变温度。

此外，超导电性还表现出Meissner效应，即超导体对外施加的磁场具有排斥作用。

这是超导体磁性行为的一个重要特征，也是超导电性应用的基础。

近年来，研究人员还发现了一类新型超导体，被称为高温超导体。

它们的超导转变温度高于传统超导体，这为更广泛的应用提供了可能性。

超导电性基础理论超导电性是一种奇特的物理现象，指的是某些材料在低温下电阻为零，电流可持续通过，而不会发生能量损失。

这种现象被广泛应用于电力输送、医疗、通信等领域。

本文将介绍超导电性的基础理论，包括超导的概念、超导材料的分类和超导现象的解释等。

超导的概念超导是指某些材料在低温下，电流的电阻为零的现象。

这种现象最早被荷兰物理学家海格夫发现，也因此称为海格夫现象。

后来，随着科学技术的发展，人们发现了很多其它具有超导现象的材料，如铜氧化物和铁基超导体等。

超导材料的分类超导材料可分为两大类： Type I 超导体和 Type II 超导体。

Type I 超导体是指自然中最早发现的超导体。

它们的临界温度一般较低（小于 -250℃），对外加磁场不太敏感，而且由于磁通的数量是量子化的，因此它们输运磁通时，磁通显得异常突出。

Type II 超导体则是指临界温度比 Type I 超导体高且对磁场灵敏度较高的超导体。

Type II 超导体可用于制造高场超导磁体等。

超导现象的解释超导现象的理论解释分为两种：凝聚态物理学中的 BCS（巴狄斯-库珀-施里弗）理论和量子场论中的 Ginzburg-Landau 理论。

BCS 理论解释超导体在低温下电阻为零的现象。

BCS 理论认为，超导体中存在一种被称为库珀对的粒子对，这种粒子对由两个电子组成。

低温下，粒子对之间会发生晶格畸变，形成一个带电的对，自由电子在这个电荷场中移动时不会受到任何阻力。

而Ginzburg-Landau 理论则是量子场论中对超导体的描述。

该理论认为，超导体中存在一种相位具有确定性的超导电子。

这种超导电子和普通电子相比，具有更高的电动势、更长的寿命和更低的能量损失。

结语超导电性是一种重要的物理现象，具有广泛应用前景。

超导电性的基础理论主要有 BCS 理论和 Ginzburg-Landau 理论，这些理论为我们深入了解超导电性提供了重要的理论支持。

随着科学技术的不断发展，超导材料的制备和应用将会得到更多的突破。

超导电性中BCS 理论的物理图像摘要：BCS 理论是从微观的角度来解释超导电性的，其中引入的库珀对的概念是理论的重要组成部分.与此同时，它能够很好的解释，一是传导电子的行为所引起的超导电性以及能隙的概念，二是晶格点阵在超导电性中所起的作用，三是超导体在临界温度时的二级相变，四是迈斯纳效应以及零电阻效应，五同位素效应..BCS 理论与从宏观上直接引入的二流体模型等有着根本的不同，前者更接近于物理实质，后者更倾向与物理现象.正文：1、零电阻超导态的零阻态是一种状态，从物理实质上有别于理想导体的电阻值为零.超导态的零电阻是从实验上观测到的，但严格上讲，我们并不能够精确测定在超导态下的电阻值是否为零.但是我们可以通过理论的解释来说明，在超导态下，导体的电阻值确属为零，也就是说电流在导体内没有衰减.这在二流体模型中或是BCS 理论中是等价的.对理想导体的电阻为零我们可以这样简单的解释：在绝对零度下，晶格的热振动停止，电子可以在晶格间毫无阻碍地自由地穿梭，从而表现为电阻值为零.需要说明的是，这里的金属是无任何杂质和缺陷的.2、 同位素效应实验上用X 光观察晶体结构，在金属温度降到临界温度以下时，晶体的晶格结构没有发生任何变化，从这一点讲，超导电性与晶体的晶格结构没有关系.但是从另一些实验上发现，对于给定的元素的不同同位素组成的样品进行测量时，会发现它们有不同的临界温度，并且满足下式[2]：T ∝M −β （1）对于不同元素的β值是不同的.这一现象称作同位素效应.3、 电子比热对于低温下正常金属的比热有以下关系[3]:C n =A (T θ)3+γT （2）其中A 是常数，T 为热力学温度，γ为索末菲常数.等号右边第一项表明的是晶格对比热的贡献，第二项为传导电子的贡献.若是在超导态下[3]:C n =A (T θ)3+ae −b/kT （3）a 、b 为常数，k 为玻尔兹曼常数.从两式中看出只有第二项发生了变化，也就是说由常态到超导态主要是传导电子的作用.4、 迈斯纳效应实验上发现，超导态下，磁场中的导体具有完全抗磁性，称为迈斯纳效应.磁场只能存在于导体表面的以薄层内，而不能深入导体内.感应电流形成的磁场将导体包围，与外磁场相消，使导体内没有磁通量.并且这个效应与形成的过程无关.对于一般导体，若磁通量发生变化，由法拉第电磁感应定律可知：V=−dΦdt =−dBdt∙S（4）在闭合回路内：V=RI+dIdt∙L（5）L为自感.由（4）（5）：−dBdt ∙S=RI+dIdt∙L（6）对于理想导体R=0，即d（BS+IL）dt=0（7）即：BS+LI=C（常数）（8）（8）式表明理想导体内的磁通量是不随外外场的变化而变化的，具有初值决定性，也就是说磁通量与导体内的初始值同大小.显然，理想导体中磁场效应与形成过程有关.5、能隙金属中的自由电子可以由能级来描述.在绝对零度下，理想导体中电子能级排布由低到高，最后占据的最高能级称作费米能级,用E F表示.在E F以下的能级全被电子占据，而在E F之上为空能级，没有电子分布.这就是金属的基态.实验表明在超导态下的金属中电子与常态下的电子分布相似，但最大的不同是在费米能级上有个宽度为2∆的间隔，称为超导能隙.在能隙下的能级完全被电子占据，在能隙上的为全空,能隙内没有电子分布.这就是超导的基态.电子若要由能级下跃迁到能级上必须有大于2∆的能量.电磁波可以激发电子跃迁到能隙之上，这就要求光子的能量hν>2∆.（a）超导能隙（b）常态基态图 1 费米能与能隙6、电子―声子相互作用电子和声子的相互作用可以把两个电子耦合在一起，就像两个电子直接作用.相互作用中一个电子发出一个声子，声子被另一个电子俘获.这种传递过程可以把两个电子“吸引”在一起，进而降低两电子的能量，这是超导能隙的来源.吸引的条件就是E1−E1，<hν.从动量角度看，如图：图 2 电子——声子若初始电子的动量分别为P 1，P 2，末态动量分别为P 1‘，P 2‘，声子动量P .则：P 1=P 1‘−P （9）P 2=P 2‘+P （10）综合以上两式，那么：P 1+P 2=P 1‘+P 2‘ （11）显然过程初态末态动量守恒.但从能量的视角看，初态到中间态，或是中间态到末态之间的能量不一定守恒.能量的不守恒，是因为这时不确定关系起作用.7、 库珀对绝对温度下理想导体的传导电子，占据费米能级下的每个态，只是每个态出现的几率不同.此时的几率分布服从费米—狄拉克分布.而对于动量，若用类似于麦克斯韦速度分布的研究方法就可以得到一个实心的半径为P F 动量球，称作费米海.如果将两个电子放在这个导体中，那么必然是这两个电子的动量都大于P F ，能量大于E F .这是因为值P F ，E F 以下的态都已经被电子占据.若是电子间有“吸引”，必然可以会使能量和低于2E F .这时就可以用简单波函数来描述这两个电子：φ（P 1，P 2）=∑a ij i ，j φij （P 1，P 2） （12）显然|a ij |2就是两个电子动量分别是P i ，P j 的几率.电子能量的最低值在E F 上一定的范围内，根据能量动量之关系E =p 2/2m ，这也就说明动量必须在费米海外Δp 内[3].对于两个电子的动量关系可以用下图来描述.P 1 P 2 P 1‘ P 2’ P图3 库珀对动量由于两电子的动量守恒，那么存在于环域内相交叉的部分的电子是成对耦合出现的，并满足一定条件.可以证明电子对的数目与体积（费米海是三维的）成正比；并且很容易证明在和动量p=0时电子对的数目有一个极大值.同时结合前面耦合电子能降低能量的叙述可知，在两电子动量大小相等方向相反的时候能量降低最大，并且此时的电子自旋一个向上一个向下，总自旋为零.这时候形成的两个电子就是库珀对.同时可以证明[3]在形成库珀对时降低的能量∆E要比电子动量（电子动量在E F之上）引起增加的能量要大.事实上，在略小于E F 的能态上的两个电子也可以形成库珀对，也就是说能量在E F附近的电子均有机会形成库珀对.在超导内，如果动量在p F附近的电子全部都形成的库珀对，使能量达到最低，若是在绝对温度下，就是超导态的基态.此时的波函数就应该简单写成下述形式：φ（P1，P2）=φ12（P1，P2）φ34（P3，P4）…φij（P i，P j）（13）显然这里的电子对按照泡利不形容原理是不符合费米—狄拉克分布的，而应为玻色—爱因斯坦分布.由于库珀对的出现，在E F附近的费米面变得模糊，而不再有清晰的分界线；若超导体在基态，必然和没有库珀对的能量值之间有一定的差值，就是2∆，即2∆=∆E，能隙的宽度.8、BCS理论BCS理论对超导态的解释，就是以库珀对为基础，超导态的成因就是库珀对的出现.传导电子在正常态下是自由的，而在超导态下就会形成库珀对.为什么形成的电子对，而不是“电子三”或多电子组.BCS理论给出了它的基本假定[3]：“与超导态有关的相互作用仅仅是使任意两个电子形成的库珀对的那些相互作用，而且所有其他电子的存在对于任何一对的影响只是通过泡利原理限制该相互作用着的对可能散射进入的那些态，因为一些态已然被占据.”9、BCS理论下的部分宏观性质1、在超导内，传导电子形成了库珀对，整体动量不变；动量形成电流，没有电流时，总动量为零.那么假设库珀对所涉及的两个电子：[(P i+p/2)↑，−(P j+p/2)↓]（14）这相当于每个电子都有p/2的动量移动，总动量为p，并且对于所有的对都一样.若观察者以p/2m运动，显然和总动量为零时看到的情况是一样的.此时电子整体运动，电流由总动量传输，[4]电流密度j=nep/2m.尽管对不断被散射，但总动量守恒，所以电流不变，即是零电阻现象.图 4 超导载流子2、在温度大于绝对零度时，超导不再是基态；随着温度的升高，库珀对的数目逐渐减少，准粒子数目增加，能隙越来越窄，直到使能隙宽度为零的温度即为临界温度.并且BCS理论给出临界温度和绝对零度下的能隙的关系：E g(0)=2∆(0)=3.5kT c.∆(0)1/2T c T c图 5 ∆对温度的变化3、临界磁场满足下列关系[3]：1=g n−g s. （15）2μ0H c2其中g n，g s分别是正常相和超导相的吉布斯自由能.在绝对零度下，式15就是正常态和超导态之间的内能密度差，同时在BCS理论下，就是库珀对的总结合能.总结：BCS理论的提出，在对超导态的解释时展示一种全新的模式，使得近半个世纪的问题得以解决.库珀对的想法，具有重要意义.上文只是对于超导态的宏观性质零电阻，迈斯纳效应等以及BCS理论中库珀对等概念给出了简单的物理文字说明；对于能隙同样做了简单的描述；对于部分宏观性质做了简单解释.就整个超导物理来说问题并没有完全解决，对于很多现象仍没有很好的解释，这需要更多的工作.[1] 王矜奉固体物理教程山东大学出版社 2003年1月[2] 章立源超越自由——神奇的超导态科学出版社 2005年7月[3] A.C.罗斯·英尼斯 E.H罗德里克超导电性导论（章立源毕金献译）人民教育出版社 1981年3月[4] 章立源超导理论科学出版社 2003年9月[5] 郭硕鸿电动力学高等教育出版社 2008年6月[6] Gerardus't Hooft寻觅基元——探索物质的终极结构（冯承天译）上海科技教育出版社2002年11月[7]J. Bardeen, L. N. Cooper, and J. R. Schrieffer Theory of Superconductivity Phys. Rev. 108, 1175–1204 (1957)。