数学(文) 第2部分 第1讲---第2节
- 格式:ppt
- 大小:1.05 MB
- 文档页数:14

高二数学选修1-1 第二章 第2节 抛物线北师大版(文)【本讲教育信息】一、教学内容选修1—1 抛物线的标准方程及其几何性质二、教学目标1、掌握抛物线定义、抛物线的标准方程四种形式及其几何性质并能熟练地应用定义、几何性质解决抛物线问题。
2、方程的数学思想、函数的数学思想、等价转化的数学思想、数与形结合的思想及待定系数法、定义法等数学思想方法的应用。
三、知识要点分析1、抛物线定义:平面内与一个定点F 和一条定直线L (L 不过F 点)的距离相等的点的集合叫抛物线。
定点F 叫做抛物线的焦点,定直线L 叫做抛物线的准线。
2、抛物线的标准方程形式:px y 22=(p>0)px y 22-=,(p>0)py x 22=,(p>0)py x 22-=(p>0)P :称为焦准距(焦点到准线的距离)3、抛物线的几何性质:对称性,X 围,顶点,离心率,(以px y 22=为例) 4、抛物线的通径:过抛物线焦点F 且垂直于对称轴的直线,与抛物线相交于P 1、P 2两点,则两交点)P P (21之间的距离就是抛物线的通径,长度是2p 。
5、有关的重要结论:设过抛物线px y 22=的焦点的直线的倾斜角是θ,与抛物线交于A (),(),,2211y x B y x 。
则有下列结论(1)|AB|=p x x ++21,|AB|=θ2sin p2,(显然当︒=θ90时,|AB|最小。
最小值是2p ,此时|AB|是抛物线的通径。
)(2)=21x x 2212,4p y y p-=(3)θsin 22p S AOB =∆(4)pBF AF 2||1||1=+(定值) (5)以|AB|为直径的圆与准线相切。
【典型例题】考点一:考查求抛物线的标准方程例1:求以原点为顶点,坐标轴为对称轴,并且经过P (-2,-4)的抛物线的标准方程及其对应的准线、焦点坐标。
【思路分析】因顶点在原点,对称轴是坐标轴,且过点P (-2,-4),故可设抛物线方程是)0(,22>-=p py x 或设)0(,22>-=p px y解:由已知设抛物线的标准方程是)0(,22>-=p py x 或)0(,22>-=p px y 把P (-2,-4)代入py x 22-=或px y 22-=得21=p 或p=4 故所求的抛物线的标准方程是x y y x 822-=-=或当抛物线方程是y x -=2时,焦点坐标是F ()41,0-,准线方程是41=y 当抛物线方程是x y 82-=时,焦点坐标是F (-2,0),准线方程是x=2 【说明】对顶点在原点,对称轴为坐标轴的抛物线方程可设为)0a (,ay x ax y 22≠==或例2:设过P (-2,4),倾斜角为π43的直线L 与抛物线C 交于A ,B 两点,抛物线C 的顶点在原点,以x 轴为对称轴,若|PA|,|AB|,|PB|成等比数列,求抛物线C 的标准方程。



课时规范练 A 组 基础对点练1.下列四个函数中,在(0,+∞)上为增函数的是( ) A .f (x )=3-x B .f (x )=x 2-3x C .f (x )=-1x +1D .f (x )=-|x |解析:当x >0时,f (x )=3-x 为减函数; 当x ∈⎝ ⎛⎭⎪⎫0,32时,f (x )=x 2-3x 为减函数,当x ∈⎝ ⎛⎭⎪⎫32,+∞时,f (x )=x 2-3x 为增函数;当x ∈(0,+∞)时,f (x )=-1x +1为增函数; 当x ∈(0,+∞)时,f (x )=-|x |为减函数.故选C. 答案:C2.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( ) A .y =1x B .y =e -x C .y =-x 2+1D .y =lg|x |解析:A 中y =1x 是奇函数,A 不正确;B 中y =e -x=⎝ ⎛⎭⎪⎫1e x 是非奇非偶函数,B不正确;C 中y =-x 2+1是偶函数且在(0,+∞)上是单调递减的,C 正确;D 中y =lg|x |在(0,+∞)上是增函数,D 不正确.故选C. 答案:C3.(2019·天津模拟)若函数f (x )满足“对任意x 1,x 2∈(0,+∞),当x 1<x 2时,都有f (x 1)>f (x 2)”,则f (x )的解析式可以是( ) A .f (x )=(x -1)2 B .f (x )=e x C .f (x )=1xD .f (x )=ln(x +1)解析:根据条件知,f (x )在(0,+∞)上单调递减.对于A ,f (x )=(x -1)2在(1,+∞)上单调递增,排除A ; 对于B ,f (x )=e x 在(0,+∞)上单调递增,排除B ; 对于C ,f (x )=1x 在(0,+∞)上单调递减,C 正确; 对于D ,f (x )=ln(x +1)在(0,+∞)上单调递增,排除D. 答案:C4.(2019·福州模拟)函数f (x )=⎩⎨⎧-x +3a ,x <0a x ,x ≥0,(a >0且a ≠1)是R 上的减函数,则a 的取值范围是( ) A .(0,1) B.⎣⎢⎡⎭⎪⎫13,1 C.⎝ ⎛⎦⎥⎤0,13 D.⎝ ⎛⎦⎥⎤0,23 解析:∵⎩⎪⎨⎪⎧0<a <13a ≥1,∴13≤a <1.答案:B5.设a >0且a ≠1,则“函数f (x )=a x 在R 上是减函数”是“函数g (x )=(2-a )x 3在R 上是增函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件 解析:若函数f (x )=a x 在R 上为减函数,则有0<a <1;若函数g (x )=(2-a )x 3在R 上为增函数,则有2-a >0,即a <2,所以“函数f (x )=a x 在R 上是减函数”是“函数g (x )=(2-a )x 3在R 上是增函数”的充分不必要条件,选A. 答案:A6.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈(-∞,0)(x 1≠x 2),都有f (x 1)-f (x 2)x 1-x 2<0.则下列结论正确的是( )A .f (0.32)<f (20.3)<f (log 25)B .f (log 25)<f (20.3)<f (0.32)C .f (log 25)<f (0.32)<f (20.3)D .f (0.32)<f (log 25)<f (20.3)解析:∵对任意的x 1,x 2∈(-∞,0),且x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0,∴f (x )在(-∞,0)上是减函数. 又∵f (x )是R 上的偶函数, ∴f (x )在(0,+∞)上是增函数, ∵0<0.32<20.3<log 25,∴f (0.32)<f (20.3)<f (log 25).故选A. 答案:AB 组 能力提升练7.定义在[-2,2]上的函数f (x )满足(x 1-x 2)[f (x 1)-f (x 2)]>0,x 1≠x 2,且f (a 2-a )>f (2a -2),则实数a 的取值范围为( ) A .[-1,2) B .[0,2) C .[0,1)D .[-1,1)解析:函数f (x )满足(x 1-x 2)[f (x 1)-f (x 2)]>0,x 1≠x 2,∴函数在[-2,2]上单调递增,∴⎩⎪⎨⎪⎧-2≤a 2-a ≤2,-2≤2a -2≤2,2a -2<a 2-a ,∴⎩⎪⎨⎪⎧-1≤a ≤2,0≤a ≤2,a <1或a >2,∴0≤a <1,故选C. 答案:C8.已知定义在R 上的函数f (x )在[1,+∞)上单调递减,且f (x +1)是偶函数,不等式f (m +2)≥f (x -1)对任意的x ∈[-1,0]恒成立,则实数m 的取值范围是( ) A .[-3,1]B .[-4,2]C .(-∞,-3]∪[1,+∞)D .(-∞,-4]∪[2,+∞)解析:因为f (x +1)是偶函数,所以f (-x +1)=f (x +1),所以f (x )的图象关于x =1对称,由f (m +2)≥f (x -1)得|(m +2)-1|≤|(x -1)-1|,所以根据题意得|m +1|≤2,解得-3≤m ≤1.故选A. 答案:A9.若函数f (x )=x 2-12ln x +1在其定义域的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是( ) A .[1,+∞) B.⎣⎢⎡⎭⎪⎫1,32 C .[1,2)D.⎣⎢⎡⎭⎪⎫32,2 解析:函数f (x )的定义域为(0,+∞),所以k -1≥0,即k ≥1.令f ′(x )=4x 2-12x =0,解得x =12⎝ ⎛⎭⎪⎫x =-12舍.因为函数f (x )在区间(k -1,k +1)内不是单调函数,所以k -1<12<k +1,得-12<k <32.综上得1≤k <32. 答案:B10.(2018·西安一中模拟)已知函数f (x )=⎩⎨⎧x 3,x ≤0,ln (x +1),x >0,若f (2-x 2)>f (x ),则实数x 的取值范围是( ) A .(-∞,-1)∪(2,+∞) B .(-∞,-2)∪(1,+∞) C .(-1,2)D .(-2,1)解析:∵当x =0时,两个表达式对应的函数值都为零,∴函数的图象是一条连续的曲线.∵当x ≤0时,函数f (x )=x 3为增函数,当x >0时,f (x )=ln(x +1)也是增函数,∴函数f (x )是定义在R 上的增函数.因此,不等式f (2-x 2)>f (x )等价于2-x 2>x ,即x 2+x -2<0,解得-2<x <1.故选D.答案:D11.若函数f (x )=|2x +a |的单调递增区间是[3,+∞),则a =________.解析:由f (x )=⎩⎪⎨⎪⎧-2x -a ,x <-a22x +a ,x ≥-a2,可得函数f (x )的单调递增区间为⎣⎢⎡⎭⎪⎫-a 2,+∞,故3=-a 2,解得a =-6.答案:-612.已知函数f (x )=x +ax (x ≠0,a ∈R ),若函数f (x )在(-∞,-2]上单调递增,则实数a 的取值范围是__________.解析:设x 1<x 2≤-2,则Δy =f (x 1)-f (x 2)=x 1+a x 1-x 2-a x 2=(x 1-x 2)⎝ ⎛⎭⎪⎫1-a x 1x 2=(x 1-x 2)(x 1x 2-a )x 1x 2.因为x 1-x 2<0,x 1x 2>0,所以要使Δy =(x 1-x 2)(x 1x 2-a )x 1x 2<0恒成立,只需使x 1x 2-a >0恒成立,即a <x 1x 2恒成立.因为x 1<x 2≤-2,所以x 1x 2>4,所以a ≤4,故函数f (x )在(-∞,-2]上单调递增时,实数a 的取值范围是(-∞,4]. 答案:(-∞,4]。

第二节基本不等式1.基本不等式:ab ≤a +b 2.(1)基本不等式成立的条件:01a >0,b >0.(2)等号成立的条件:当且仅当02a =b 时,等号成立.(3)其中03a +b2叫做正数a ,b 的算术平均数,04ab 叫做正数a ,b 的几何平均数.2.几个重要的不等式(1)a 2+b 205≥2ab (a ,b ∈R ).(2)b a +ab 06≥2(a ,b同号).(3)(a ,b ∈R ).(a ,b ∈R ).以上不等式等号成立的条件均为09a =b .3.利用基本不等式求最值(1)已知x ,y 都是正数,如果积xy 等于定值P ,那么当10x =y 时,和x +y 有最小值112P .(简记:积定和最小)(2)已知x ,y 都是正数,如果和x +y 等于定值S ,那么当12x =y 时,积xy 有最大值1314S 2.(简记:和定积最大)注意:(1)利用基本不等式求最值应满足三个条件“一正、二定、三相等”,其中“一正”指正数,“二定”指求最值时和或积为定值,“三相等”指满足等号成立的条件.(2)形如y =x +ax (a >0)的函数求最值时,首先考虑用基本不等式,若等号取不到,再利用该函数的单调性求解.1.连续使用基本不等式求最值要求每次等号成立的条件要一致.2.若a >0,b >0,则21a +1b ≤ab ≤a +b2≤a 2+b 22,当且仅当a =b 时,等号成立.3.常见求最值的模型模型一:mx +nx≥2mn (m >0,n >0,x >0),当且仅当x =nm时,等号成立;模型二:mx +n x -a =m (x -a )+nx -a +ma ≥2mn +ma (m >0,n >0,x >a ),当且仅当x -a =n m时,等号成立;模型三:xax 2+bx +c =1ax +b +c x ≤12ac +b(a >0,c >0,x >0),当且仅当x =ca时,等号成立;模型四:x (n -mx )=mx (n -mx )m ≤1m ·>0,n >0,0<x 当且仅当x =n 2m时,等号成立.4.三个正数的均值不等式:若a ,b ,c >0,则a +b +c 3≥3abc ,当且仅当a =b =c 时,等号成立.1.概念辨析(正确的打“√”,错误的打“×”)(1)y =x +1x 的最小值是2.()(2)|b a +a b |≥2.()(3)已知0<x <12,则x (1-2x )的最大值为18.()(4)函数f (x )=sin x +4sin x 的最小值为4.()答案(1)×(2)√(3)√(4)×2.小题热身(1)设a >0,则9a +1a 的最小值为()A .4B .5C .6D .7答案C 解析9a +1a≥29a ·1a =6,当且仅当9a =1a ,即a =13时,等号成立.(2)矩形两边长分别为a ,b ,且a +2b =6,则矩形面积的最大值是()A .4 B.92C.322D .2答案B解析依题意,可得a >0,b >0,则6=a +2b ≥2a ·2b =22·ab ,当且仅当a =2b 时取等号,所以ab ≤628=92,即矩形面积的最大值为92.故选B.(3)(2024·河南郑州高三模拟)已知实数a >0,b >0,a +b =2,则1a +ab 的最小值为________.答案12+2解析1a +a b =12×a +b a +a b =12+b 2a +a b ≥12+2b 2a ·a b =12+2,当且仅当b 2a =ab,即a =22-2,b =4-22时,等号成立.(4)(人教A 必修第一册习题2.2T1(2)改编)函数y =x (3-2x )(0≤x ≤1)的最大值是________.答案98解析因为0≤x ≤1,所以3-2x >0,所以y =12·2x ·(3-2x )≤122x +(3-2x )22=98,当且仅当2x =3-2x ,即x =34时取等号.(5)(人教A 必修第一册复习参考题2T5改编)已知a ,b >0,且ab =a +b +3,则ab 的取值范围为________.答案[9,+∞)解析因为a,b>0,所以ab-3=a+b≥2ab,于是ab-2ab-3≥0,解得ab≤-1(舍去)或ab≥3,所以ab≥9,当且仅当a=b=3时,等号成立,所以ab的取值范围是[9,+∞).考点探究——提素养考点一利用基本不等式求最值(多考向探究)考向1配凑法求最值例1(1)(2024·福建福州四校高三期中联考)已知0<x<2,则y=x4-x2的最大值为() A.2B.4C.5D.6答案A解析因为0<x<2,所以y=x4-x2=x2(4-x2)≤x2+(4-x2)2=2,当且仅当x2=4-x2,即x=2时,等号成立,即y=x4-x2的最大值为2.故选A.(2)函数y=x2+3x+3x+1(x<-1)的最大值为()A.3B.2C.1D.-1答案D解析y=x2+3x+3x+1=(x+1)2+(x+1)+1x+1=--(x+1)+1-(x+1)+1≤-1=-1,当且仅当x+1=1x+1=-1,即x=-2时,等号成立.故选D.【通性通法】配凑法求最值的关键点【巩固迁移】1.函数y =3x ()A .8B .7C .6D .5答案D解析因为x >13,所以3x -1>0,所以y =3x +43x -1=(3x -1)+43x -1+1≥2(3x -1)·43x -1+1=5,当且仅当3x -1=43x -1,即x =1时,等号成立,故函数y =3x 值为5.故选D.2.(2023·浙江杭州高三教学质量检测)已知a >1,b >1,且log 2a =log b 4,则ab 的最小值为()A .4B .8C .16D .32答案C解析∵log 2a =log b 4,∴12log 2a =log b 4,即log 2a =2log 24log 2b ,∴log 2a ·log 2b =4.∵a >1,b >1,∴log 2a >0,log 2b >0,∴log 2(ab )=log 2a +log 2b ≥2log 2a ·log 2b =4,当且仅当log 2a =log 2b =2,即a =b =4时取等号,所以ab ≥24=16,当且仅当a =b =4时取等号,故ab 的最小值为16.故选C.考向2常数代换法求最值例2(1)已知0<x <1,则9x +161-x 的最小值为()A .50B .49C .25D .7答案B解析因为0<x <1,所以9x +161-x =(x +1-x )25+9(1-x )x+16x 1-x ≥25+29(1-x )x ·16x 1-x =49,当且仅当9(1-x )x=16x 1-x ,即x =37时,等号成立,所以9x +161-x 的最小值为49.故选B.(2)已知a >0,b >0,a +2b =3,则1a +1b 的最小值为()A.223B.233C .1+223D .1+233答案C解析因为a +2b =3,所以13a +23b =1,+23b =13+23+a 3b +2b 3a≥1+2a 3b ·2b3a=1+223,当且仅当a 3b =2b3a ,即a =3(2-1),b =3(2-2)2时,等号成立.故选C.【通性通法】常数代换法求最值的基本步骤【巩固迁移】3.若正实数x ,y 满足2x +y =9,则-1x -4y 的最大值是()A.6+429B .-6+429C .6+42D .-6-42答案B解析因为1x +4y =19x +y )+y x +8x y+6+429,当且仅当y x =8xy ,即x =9(2-1)2,y =9(2-2)时,等号成立,所以-1x -4y ≤-6+429.故选B.4.(2024·湖北荆门三校高三联考)已知实数a ,b 满足lg a +lg b =lg (a +2b ),则2a +b 的最小值是()A .5B .9C .13D .18答案B解析由lg a +lg b =lg (a +2b ),可得lg (ab )=lg (a +2b ),所以ab =a +2b ,即2a +1b =1,且a >0,b >0,则2a +b =(2a +b 5+2b a +2ab ≥5+22b a ·2a b =9,当且仅当2b a =2ab,即a =b =3时,等号成立,所以2a +b 的最小值为9.故选B.考向3消元法、换元法求最值例3(1)已知5x 2y 2+y 4=1(x ,y ∈R ),则x 2+y 2的最小值是()A.14B.45C.255D .2答案B解析因为5x 2y 2+y 4=1,所以x 2=1-y 45y 2,又x 2≥0,所以y 2∈(0,1],所以x 2+y 2=y 2+1-y 45y2=4y 4+15y 2=y 2≥15×24y 2·1y 2=45,当且仅当4y 2=1y 2,即y 2=12,x 2=310时取等号,所以x 2+y 2的最小值是45.故选B.(2)(2024·浙江嘉兴第一中学高三期中)若x >0,y >0,且1x +1+1x +2y=1,则2x +y 的最小值为()A .2B .23C.12+3D .4+23答案C解析设x +1=a ,x +2y =b ,则x =a -1,y =b -a +12,且a >0,b >0,则1a +1b =1,2x +y=2(a -1)+b -a +12=3a +b 2-32,而3a +b =(3a +b 4+3a b +ba ≥4+23a b ·ba=4+23,当且仅当3a b =ba ,即a =3+33,b =3+1时,等号成立,则2x +y ≥4+232-32=12+ 3.故选C.【通性通法】当所求最值的代数式中变量比较多时,通常考虑利用已知条件消去部分变量后,凑出“和为常数”或“积为常数”的形式,最后利用基本不等式求最值.【巩固迁移】5.(2023·江苏南京高三调研)设a ≥0,b ≥0,且2a +b =1,则ab 的最小值为__________.答案解析因为2a +b =1,所以a =(b -1)24,所以a b =(b -1)24b=b 4+14b -12≥2b 4·14b-12=0,当且仅当a =0,b =1时取等号.6.(2024·湖北襄阳五中高三质量检测)若正数a ,b 满足2a +b =1,则a 2-2a +b2-b的最小值是________.答案223-12解析设u =2-2a ,v =2-b ,则a =2-u 2,b =2-v ,则u +v =3(u >0,v >0),所以a 2-2a +b2-b=1-12u u+2-v v =1u +2v -32=13(u +v 32+v u +-32+321+223-32=223-12,当且仅当v =6-32,u =32-3时,等号成立,所以a 2-2a +b 2-b 的最小值为223-12.考向4“和”“积”互化求最值例4(多选)设a >1,b >1,且ab -(a +b )=1,那么()A .a +b 有最小值22+2B .a +b 有最大值22-2C .ab 有最大值3-22D .ab 有最小值3+22答案AD解析∵a >1,b >1,∴ab -1=a +b ≥2ab ,当a =b 时取等号,即ab -2ab -1≥0,解得ab ≥2+1,∴ab ≥(2+1)2=3+22,∴ab 有最小值3+2 2.又ab ,当a =b 时取等号,∴1=ab -(a +b )-(a +b ),即(a +b )2-4(a +b )≥4,则[(a +b )-2]2≥8,解得a +b -2≥22,即a +b ≥22+2,∴a +b 有最小值22+2.故选AD.【通性通法】“和”“积”互化求最值的方法(1)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,因此可以用在一些不等式的证明中,还可以用于求代数式的最值.(2)如果条件中含有两个变量的和与积的形式,可以直接利用基本不等式对两个正数的和与积进行转化,然后通过解不等式进行求解,或者通过构造一元二次方程,利用根的分布解决问题.【巩固迁移】7.正实数x ,y 满足4x 2+y 2+xy =1,则xy 的最大值为________,2x +y 的最大值为________.答案152105解析∵1-xy =4x 2+y 2≥4xy ,∴5xy ≤1,∴xy ≤15,当且仅当y =2x ,即x =1010,y =105时取等号.∵4x 2+y 2+xy =1,∴(2x +y )2-3xy =1,∴(2x +y )2-1=3xy =32·2x ·y,即(2x +y )2-1≤38(2x +y )2,∴(2x +y )2≤85,∴2x +y ≤2105,当且仅当2x =y ,即x =1010,y=105时取等号.考点二基本不等式的综合应用例5(2024·河南濮阳外国语学校模拟)若对任意正数x ,不等式2x 2+4≤2a +1x恒成立,则实数a 的取值范围为()A .[0,+∞) B.-14,+∞C.14,+∞ D.12,+∞答案B解析依题意得,当x >0时,2a +1≥2x x 2+4=2x +4x恒成立,又x +4x ≥4,当且仅当x =2时取等号,所以2x +4x 的最大值为12,所以2a +1≥12,解得实数a 的取值范围为-14,+故选B.【通性通法】1.利用基本不等式求参数的值或范围时,要观察题目的特点,先确定是恒成立问题还是有解问题,再利用基本不等式确定等号成立的条件,最后通过解不等式(组)得到参数的值或范围.2.当基本不等式与其他知识相结合时,往往是为其他知识提供一个应用基本不等式的条件,然后利用常数代换法求最值.【巩固迁移】8.在等腰三角形ABC 中,AB =AC ,若AC 边上的中线BD 的长为3,则△ABC 面积的最大值是()A .6B .12C .18D .24答案A解析设AB =AC =2m ,BC =2n ,因为∠ADB =π-∠CDB ,所以m 2+9-4m 26m =-m 2+9-4n 26m,整理得m 2=9-2n 2.设△ABC 的面积为S ,则S =12BC =12×2n ×4m 2-n 2=3n 4-n 2=3n 2(4-n 2)≤3×n 2+4-n 22=6,当且仅当n =2时,等号成立.故选A.考点三基本不等式的实际应用例6网店和实体店各有利弊,两者的结合将在未来一段时期内成为商业的一个主要发展方向.某品牌行车记录仪支架销售公司从2022年10月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量x (万件)与投入实体店体验安装的费用t (万元)之间满足函数关系式x =3-2t +1.已知网店每月固定的各种费用支出为3万元,产品每1万件进货价格为32万元,若每件产品的售价定为“进货价的150%”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润是________万元.答案37.5解析由题意知t =23-x-1(1<x <3),设该公司的月利润为y 万元,则y -32x -3-t =16x -t 2-3=16x -13-x +12-3=45.5-16(3-x )+13-x ≤45.5-216=37.5,当且仅当x =114时取等号,即最大月利润为37.5万元.【通性通法】利用基本不等式解决实际应用问题的技巧【巩固迁移】9.一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买10g 黄金,售货员先将5g 的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将5g 的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.若顾客实际购得的黄金为m g ,则()A .m >10B .m =10C .m <10D .以上都有可能答案A解析由于天平两臂不等长,可设天平左臂长为a ,右臂长为b ,则a ≠b ,设先称得黄金为xg ,后称得黄金为y g ,则bx =5a ,ay =5b ,∴x =5a b ,y =5b a ,∴x +y =5a b +5ba=5×2a b ·b a =10,当且仅当a b =ba,即a =b 时,等号成立,但a ≠b ,等号不成立,即x +y >10.因此顾客实际购得的黄金克数m >10.故选A.课时作业一、单项选择题1.当x <0时,函数y =x +4x ()A .有最大值-4B .有最小值-4C .有最大值4D .有最小值4答案A解析y =x +4x=-(-x )-4,当且仅当x =-2时,等号成立.故选A.2.(2023·陕西咸阳高三模拟)已知x >0,y >0,若2x +y =8xy ,则xy 的最小值是()A.18B.14C.24D.22答案A解析因为2x +y ≥22xy ,所以8xy ≥22xy ,解得xy ≥18,当且仅当2x =y ,即x =14,y =12时,等号成立.故选A.3.已知F 1,F 2是椭圆C :x 29+y 24=1的两个焦点,点M 在C 上,则|MF 1|·|MF 2|的最大值为()A .13B .12C .9D .6答案C解析由椭圆的定义可知,|MF 1|+|MF 2|=2a =6.由基本不等式可得|MF 1|·|MF 2|=9,当且仅当|MF 1|=|MF 2|=3时,等号成立.故选C.4.(2024·浙江绍兴第一中学高三期中)已知直线ax +by -1=0(ab >0)过圆(x -1)2+(y -2)2=2024的圆心,则1a +1b 的最小值为()A .3+22B .3-22C .6D .9答案A解析由圆的方程知,圆心为(1,2).∵直线ax +by -1=0(ab >0)过圆的圆心,∴a +2b =1(ab >0),∴1a +1b =(a +2b )=3+a b +2ba≥3+2a b ·2b a=3+当且仅当a b =2ba,即a =2b ,∴1a +1b的最小值为3+2 2.故选A.5.(2023·湖南五市十校联考)原油作为“工业血液”“黑色黄金”,其价格的波动牵动着整个化工产业甚至世界经济.小李在某段时间内共加油两次,这段时间燃油价格有升有降,现小李有两种加油方案:第一种方案是每次加油40升,第二种方案是每次加油200元,则下列说法正确的是()A .第一种方案更划算B .第二种方案更划算C .两种方案一样D .无法确定答案B解析设小李这两次加油的油价分别为x 元/升、y 元/升(x ≠y ),则第一种方案:两次加油的平均价格为40x +40y 80=x +y 2>xy ,第二种方案:两次加油的平均价格为400200x +200y =2xyx +y <xy ,故无论油价如何起伏,第二种方案都比第一种方案更划算.故选B.6.(2023·浙江杭州调研)对任意m ,n ∈(0,+∞),都有m 2-amn +2n 2≥0,则实数a 的最大值为()A .4 B.92C.2D .22答案D 解析由m 2-amn +2n 2≥0得m 2+2n 2≥amn ,即a ≤m 2+2n 2mn=m n +2n m 恒成立,因为m n +2nm≥2m n ·2n m =22,当且仅当m n =2nm,即m =2n 时取等号,所以a ≤22,故实数a 的最大值为2 2.故选D.7.(2024·浙江名校协作体高三模拟)设x ,y 为正实数,若2x +y +2xy =54,则2x +y 的最小值是()A .4B .3C .2D .1答案D解析因为x ,y 为正实数,且54=2x +y +2xy =(2x +1)(y +1)-1,令m =2x +1,n =y +1,则mn =94,所以2x +y =m +n -2≥2mn -2=1,当且仅当m =n ,即y =12,x =14时取等号.故选D.8.(2024·湖北襄阳第四中学高三适应性考试)若a ,b ,c 均为正数,且满足a 2+2ab +3ac +6bc =1,则2a +2b +3c 的最小值是()A .2B .1C.2D .22答案A解析因为a 2+2ab +3ac +6bc =1,所以a (a +2b )+3c (a +2b )=(a +2b )(a +3c )=1,又a ,b ,c 均为正数,(a +2b )(a +3c )=(2a +2b +3c )24,当且仅当a +2b =a +3c =1时取等号,所以(2a+2b+3c)24≥1,即2a+2b+3c≥2.故选A.二、多项选择题9.下列四个函数中,最小值为2的是()A.y=sin xxB.y=ln x+1ln x(x>0,x≠1)C.y=x2+6 x2+5D.y=4x+4-x 答案AD解析对于A,因为0<x≤π2,所以0<sin x≤1,则y=sin x+1sin x≥2,当且仅当sin x=1sin x,即sin x=1时取等号,故y=sin x x2,符合题意;对于B,当0<x<1时,ln x<0,此时y=ln x+1ln x为负值,无最小值,不符合题意;对于C,y=x2+6x2+5=x2+5+1x2+5,设t=x2+5,则t≥5,则y≥5+15=655,其最小值不是2,不符合题意;对于D,y=4x+4-x=4x+14x≥24x·14x=2,当且仅当x=0时取等号,故y=4x+4-x的最小值为2,符合题意.故选AD.10.(2024·湖北部分名校高三适应性考试)已知正实数a,b满足ab+a+b=8,下列说法正确的是()A.ab的最大值为2B.a+b的最小值为4C.a+2b的最小值为62-3D.1a(b+1)+1b的最小值为12答案BCD解析对于A,因为ab+a+b=8≥ab+2ab,即(ab)2+2ab-8≤0,解得0<ab≤2,则ab≤4,当且仅当a=b=2时取等号,故A错误;对于B,ab+a+b=8≤(a+b)24+(a+b),即(a+b)2+4(a+b)-32≥0,解得a+b≤-8(舍去),a+b≥4,当且仅当a=b=2时取等号,故B正确;对于C,由题意可得b(a+1)=8-a,所以b=8-aa+1>0,解得0<a<8,a+2b=a+2·8-a a +1=a +18a +1-2=a +1+18a +1-3≥2(a +1)·18a +1-3=62-3,当且仅当a +1=18a +1,即a =32-1时取等号,故C 正确;对于D ,因为1a (b +1)+1b =181a (b +1)+1b [a (b +1)+b ]=182+b a (b +1)+a (b +1)b ≥18+2)=12,当且仅当b a (b +1)=a (b +1)b ,即b =4,a =45时取等号,故D 正确,故选BCD.11.已知a >0,b >0,且a +b =1,则()A .a 2+b 2≥12B .2a -b >12C .log 2a +log 2b ≥-2D.a +b ≤2答案ABD解析对于A ,a 2+b 2=a 2+(1-a )2=2a 2-2a +1=+12≥12,当且仅当a =b =12时,等号成立,故A 正确;对于B ,a -b =2a -1>-1,所以2a -b >2-1=12,故B 正确;对于C ,log 2a +log 2b =log 2ab ≤log=log 214=-2,当且仅当a =b =12时,等号成立,故C 不正确;对于D ,因为(a +b )2=1+2ab ≤1+a +b =2,所以a +b ≤2,当且仅当a =b =12时,等号成立,故D 正确.故选ABD.三、填空题12.(2023·山东滨州三校联考)若函数f (x )=x +1x -2(x >2)在x =a 处取最小值,则a =________.答案3解析当x >2时,x -2>0,f (x )=(x -2)+1x -2+2≥2(x -2)·1x -2+2=4,当且仅当x -2=1x -2(x >2),即x =3时取等号,即当f (x )取得最小值时,x =3,即a =3.13.(2024·河北衡水中学高三第三次综合素养评价)已知实数a >b >1,满足a +1a -1≥b +1b -1,则a +4b 的最小值是________.答案9解析由已知条件,得a -b ≥1b -1-1a -1=(a -1)-(b -1)(b -1)(a -1)=a -b (b -1)(a -1),∵a -b >0,∴1≥1(b -1)(a -1),又a -1>0,b -1>0,∴(b -1)(a -1)≥1,∴a +4b =(a -1)+4(b -1)+5≥2(a -1)·4(b -1)+5=9,-1=4(b -1),-1)(a -1)=1,=3,=32时,等号成立.14.(2023·湖北荆宜三校高三模拟)已知正数a ,b 满足a +3b +3a +4b =18,则a +3b 的最大值是________.答案9+36解析设t =a +3b ,则3a +4b =18-t ,所以t (18-t )=(a +3b 15+9b a +4ab≥15+29b a ·4ab=27,当且仅当2a =3b 时取等号.所以t 2-18t +27≤0,解得9-36≤t ≤9+36,即a +3b 的最大值是9+36,当且仅当2a =3b ,即a =3+6,b =2+263时取等号.15.(2024·浙江名校联盟高三上学期第一次联考)已知正实数x ,y 满足1x +4y +4=x +y ,则x+y 的最小值为()A.13-2B .2C .2+13D .2+14答案C解析因为正实数x ,y 满足1x +4y+4=x +y ,等式两边同乘以x +y ,可得(x +y )2=4(x +y )+5+y x +4xy≥4(x +y )+5+2y x ·4xy =4(x +y )+9,所以(x +y )2-4(x +y )-9≥0,因为x +y >0,所以x +y ≥2+13,当且仅当y =2x 时,等号成立.因此x +y 的最小值为2+13.故选C.16.已知点E 是△ABC 的中线BD 上的一点(不包括端点),若AE →=xAB →+yAC →,则2x +1y 的最小值为()A .4B .6C .8D .9答案C解析设BE →=λBD →(0<λ<1),∵AE →=AB →+BE →=AB →+λBD →=AB →+λ(AD →-AB →)=(1-λ)AB →+λ2AC →,∴x =1-λ,y =λ2(x >0,y >0),∴2x +1y =21-λ+2λ=-λ)+λ]=4+2λ1-λ+2(1-λ)λ≥4+22λ1-λ·2(1-λ)λ=8,当且仅当2λ1-λ=2(1-λ)λ,即λ=12时取等号,故2x +1y 的最小值为8.故选C.17.(多选)(2022·新高考Ⅱ卷)若x ,y 满足x 2+y 2-xy =1,则()A .x +y ≤1B .x +y ≥-2C .x 2+y 2≤2D .x 2+y 2≥1答案BC解析由x 2+y 2-xy =1得(x +y )2-1=3xy ≤,解得-2≤x +y ≤2,当且仅当x =y =-1时,x +y =-2,当且仅当x =y =1时,x +y =2,所以A 错误,B 正确;由x 2+y 2-xy =1得x 2+y 2-1=xy ,又x 2+y 2≥2x 2·y2=2|xy |,所以|x 2+y 2-1|≤x2+y 22即-x 2+y 22≤x 2+y 2-1≤x 2+y 22,所以23≤x 2+y 2≤2,当且仅当x =y =±1时,x 2+y 2=2,当x =33,y =-33或x =-33,y =33时,x 2+y 2=23,所以C 正确,D 错误.故选BC.18.(多选)(2024·湖北襄阳第五中学高三月考)若a >b >0,且a +b =1,则()A .2a +2b ≥22B .2a +ab ≥2+22C .(a 2+1)(b 2+1)<32D .a 2a +2+b 2b +1≥14答案BD解析因为a >b >0,且a +b =1,所以0<b <12,12<a <1.对于A ,因为2a +2b ≥22a ·2b =22a +b=22,当且仅当a =b =12时取等号,但a >b >0,所以等号取不到,故A 错误;对于B ,因为b a >0,a b >0,由基本不等式,得2a +a b =2a +2b a +a b =2+2b a +a b ≥2+22b a ·ab=2+22,当且仅当2b a =a b ,即a =2-2,b =2-1时,等号成立,所以2a +ab≥2+22,故B 正确;对于C ,因为a +b =1,所以(a 2+1)(b 2+1)=a 2b 2+a 2+b 2+1=a 2b 2+(a +b )2-2ab +1=a 2b 2-2ab +2=(ab -1)2+1,其中ab ≤(a +b )24=14,当且仅当a =b 时取等号,但a >b >0,所以等号取不到,所以0<ab <14,(a 2+1)(b 2+1)=(ab -1)2+1故C 错误;对于D ,a 2a +2+b 2b +1=[(a +2)-2]2a +2+[(b +1)-1]2b +1=(a +2)+4a +2-4+(b +1)+1b +1-2=4a +2+1b +1-2,因为a +b=1,所以a +2+b +1=4,故a +24+b +14=1,所以4a +2+1b +1==1+14+b +1a +2+a +24(b +1)≥54+2b +1a +2·a +24(b +1)=94,当且仅当b +1a +2=a +24(b +1),即a =23,b =13时,等号成立,所以a 2a +2+b 2b +1=4a +2+1b +1-2≥94-2=14,故D 正确.故选BD.19.(2024·湖北百校高三联考)已知正数x ,y 满足3x +4y =4,则y是________.答案1解析因为x ,y 是正数,所以=y xy +3+y 2xy +1=1x +3y +12x +1y,且x +3y +2x +1y =3x +4y =4,所以y=14+3y +2x·=+2x +1y x +3y +≥14×(2+2)=1,当且仅当2x +1y x +3y =x +3y 2x +1y,即x =45,y =52,等号成立,所以y 1.20.(2023·广东深圳高三二模)足球是一项很受欢迎的体育运动.如图,某标准足球场的底线宽AB =72码,球门宽EF =8码,球门位于底线的正中位置.在比赛过程中,攻方球员带球运动时,往往需要找到一点P ,使得∠EPF 最大,这时候点P 就是最佳射门位置.当攻方球员甲位于边线上的点O 处(OA =AB ,OA ⊥AB )时,根据场上形势判断,有OA →,OB →两条进攻线路可供选择.若选择线路OA →,则甲带球________码时,到达最佳射门位置;若选择线路OB →,则甲带球________码时,到达最佳射门位置.答案72-165722-165解析若选择线路OA →,设AP =t ,其中0<t ≤72,AE =32,AF =32+8=40,则tan ∠APE =AEAP=32t ,tan ∠APF =AF AP =40t ,所以tan ∠EPF =tan(∠APF -∠APE )=tan ∠APF -tan ∠APE 1+tan ∠APF tan ∠APE=40t -32t 1+1280t 2=8t 1+1280t2=8t +1280t ≤82t ·1280t =520,当且仅当t =1280t ,即t =165时,等号成立,此时OP =OA -AP =72-165,所以若选择线路OA →,则甲带球72-165码时,到达最佳射门位置;若选择线路OB →,以线段EF 的中点N 为坐标原点,BA →,AO →的方向分别为x ,y 轴正方向建立如图所示的空间直角坐标系,则B (-36,0),O (36,72),F (-4,0),E (4,0),k OB =7236+36=1,直线OB 的方程为y =x +36,设点P (x ,x +36),其中-36<x ≤36,tan ∠AFP =k PF =x +36x +4,tan ∠AEP =k PE =x +36x -4,所以tan ∠EPF =tan(∠AEP -∠AFP )=tan ∠AEP -tan ∠AFP1+tan ∠AEP tan ∠AFP=x +36x -4-x +36x +41+x +36x -4·x +36x +4=8(x +36)x 2-161+(x +36)2x 2-16=8(x +36)+x 2-16x +36,令m =x +36∈(0,72],则x =m -36,所以x +36+x 2-16x +36=m +(m -36)2-16m =2m +1280m -72≥22m ·1280m72=3210-72,当且仅当2m =1280m,即m =810,即x =810-36时,等号成立,所以tan ∠EPF =82m+1280m-72≤83210-72=1410-9,当且仅当x=810-36时,等号成立,此时|OP|=2·|36-(810-36)|=722-165,所以若选择线路OB→,则甲带球722-165码时,到达最佳射门位置.。

第2章《整式的加减》教案一、课标要求1、知识与技能(1)理解并掌握单项式、多项式和整式的概念,弄清它们之间的区别于联系;(2)理解同类项的概念,掌握合并同类项的方法,掌握去括号时的符号变化的规律,能正确掌握多项式的概念,进而理解整式的概念。
(3)掌握多项式的项数,次数的概念,并能熟练地说出多项式的项数和次数。
(4)会用多项式表示简单的数量关系,并根据多项式中字母的值求多项式的值。
(5)会利用合并同类项将整式化简求值。
会运用整式的加减解决简单的实际问题(6)应用整式和整式的加减运算表示实际问题中的数量关系。
2、过程与方法(1)掌握从特殊到一般,从个体到整体地观察、分析问题的方法。
尝试从不同角度探究问题,培养应用意识和创新意识。
(2)经过探索有理数运算法则和运算律的过程,体会“类比”、“转化”、“数形结合”等数学方法。
3.情感、态度与价值观使学生感受数学知识与现实世界的联系,鼓励学生探索规律,并在合作交流中完善规范语言。
二、本章教材分析1.主要内容:1.本单元结合学生的生活经验,列举了学生熟悉的从数到式表示的实例,•从扩充运算的角度引入单项式与多项式的概念,然后再指出可以用单项式与多项式表示现实生活中具有意义的关系,使学生感受到整式的引入是来自实际生活的需要,体会数学知识与现实世界的联系。
引入整式概念之后,接着给出单项式与多项式的概念。
2.通过怎样用单项式与多项式关系引入整式。
整式的运算是非常重要的数学工具,在揭示了数形之间的内在联系,从而体现出以下4个方面的作用:(1)单项式与多项式之间的内在关系;(2)单项式与多项式的有关概念;(3)单项式与多项式的运算;(4)在实际问题中,单项式与多项式的表现形式;3.应用整式和整式的加减运算表示实际问题中的数量关系。
掌握从特殊到一般,从个体到整体地观察、分析问题的方法。
尝试从不同角度探究问题,培养应用意识和创新意识。
2.本单元在教材中的地位与作用:1、梳理整式的相关概念,归纳概念之间的区别与联系。

高二数学选修一第二章知识点梳理第一节函数的概念和性质1. 函数的定义函数是一个数集到另一个数集的映射关系,通常表示为f(x),其中x是自变量,f(x)是函数值或因变量。
函数的定义域是自变量的取值范围,值域是因变量的取值范围。
2. 函数的表示方法函数可以用公式、图像、表格和文字描述等方式进行表示。
其中,公式表示最常见,如f(x) = 2x + 1。
3. 函数的性质函数有奇偶性、单调性、周期性等性质。
例如,奇函数满足f(-x) = -f(x),偶函数满足f(-x) = f(x)。
第二节一次函数与二次函数1. 一次函数一次函数又称为线性函数,可表示为f(x) = ax + b,其中a和b 为常数。
一次函数的图像为一条直线,斜率a表征了直线的倾斜程度。
2. 二次函数二次函数可表示为f(x) = ax^2 + bx + c,其中a、b和c为常数且a ≠ 0。
二次函数的图像为抛物线,开口方向取决于a的正负。
第三节指数函数与对数函数1. 指数函数指数函数可表示为f(x) = a^x,其中a为底数,x为指数。
指数函数的图像以底数为基准,增长或衰减速度取决于底数的大小。
2. 对数函数对数函数可表示为f(x) = logₐx,其中a为底数,x为真数。
对数函数与指数函数是互逆关系,即logₐaⁿ = n。
第四节三角函数1. 正弦函数、余弦函数和正切函数三角函数常用的有正弦函数sin(x)、余弦函数cos(x)和正切函数tan(x)。
它们的周期均为2π,具有周期性质。
2. 三角函数的性质三角函数具有周期性、奇偶性和单调性等性质。
例如,正弦函数和余弦函数是奇函数,正切函数是奇函数。
第五节极坐标与参数方程1. 极坐标系极坐标系使用极径和极角来表示平面上的点,其中极径表示点到原点的距离,极角表示点与极轴的角度。
2. 参数方程参数方程使用参数t表示自变量,以x和y关于t的函数形式来定义曲线上的点。
参数方程常用于描述非线性曲线。

苏教版6年级数学上册第2单元第1课《分数与整数相乘》教案一. 教材分析苏教版六年级数学上册第二单元第一课《分数与整数相乘》是本册教材中分数乘法部分的重要内容。
通过本节课的学习,让学生掌握分数与整数相乘的计算法则,理解在乘法运算中,整数与分数相乘,分子与整数相乘的规律,发展学生的数学思维能力。
二. 学情分析学生在五年级时已经学习了分数的加减法和乘除法,对分数的概念和运算有一定的了解。
但六年级的学生在理解和运用分数乘法运算时,仍存在一定的困难。
因此,在教学过程中,要关注学生的知识基础,针对学生的实际情况进行有针对性的教学。
三. 教学目标1.理解分数与整数相乘的计算法则,掌握分数与整数相乘的运算方法。
2.能够正确进行分数与整数相乘的计算,解决实际问题。
3.培养学生的数学思维能力,提高学生的数学素养。
四. 教学重难点1.教学重点:分数与整数相乘的计算法则,分数与整数相乘的运算方法。
2.教学难点:理解分数与整数相乘时,分子与整数相乘的规律。
五. 教学方法采用情境教学法、启发式教学法、小组合作学习法等,激发学生的学习兴趣,引导学生主动探究,培养学生的动手操作能力和思维能力。
六. 教学准备1.教学课件:分数与整数相乘的动画演示、例题和练习题。
2.学具:白纸、彩笔、剪刀、胶水等。
3.教学素材:生活中的分数乘法问题。
七. 教学过程导入(5分钟)1.创设情境:教师出示一个水果拼盘,其中有3个苹果,每个苹果上切了2刀,共切了6块。
让学生观察并回答:这个水果拼盘里有几块水果?2.学生回答后,教师引导学生思考:如果把这个水果拼盘分给6个同学,每个人能分到几块水果?呈现(10分钟)1.教师通过课件展示分数与整数相乘的算式:3 × 1/22.引导学生观察算式,提问:这个算式表示什么意思?3.学生回答后,教师解释:这个算式表示3个1/2相加的结果。
操练(10分钟)1.学生自主完成教材中的例题:4 × 3/52.教师引导学生思考:在计算这个算式时,应该如何操作?3.学生回答后,教师讲解:分数与整数相乘,相当于分数的分子与整数相乘,分母保持不变。

人教版二年级上册数学第2单元第1课时《两位数加一位数(不进位)》教案一. 教材分析《两位数加一位数(不进位)》是人教版二年级上册数学第2单元的第1课时,本节课主要让学生掌握两位数加一位数(不进位)的计算方法,为学生后续学习两位数加一位数(进位)和三位数加两位数等加法运算打下基础。
教材通过生动的图片和实际情境,引导学生理解和掌握加法运算的原理。
二. 学情分析学生在一年级时已经学习了10以内数的加法,对加法运算有了一定的认识。
但二年级的学生对两位数加一位数的计算方法还不够熟悉,需要通过实例和练习来进一步理解和掌握。
此外,学生可能对进位概念理解不够,需要在教学中进行引导和解释。
三. 教学目标1.让学生理解两位数加一位数(不进位)的计算方法,并能熟练进行计算。
2.培养学生独立思考、合作交流的能力。
3.培养学生对数学的兴趣,提高学生解决实际问题的能力。
四. 教学重难点1.教学重点:两位数加一位数(不进位)的计算方法。
2.教学难点:对进位概念的理解和应用。
五. 教学方法采用情境教学法、游戏教学法和小组合作学习法。
通过生动的情景和游戏,激发学生的学习兴趣,引导学生主动参与计算实践,培养学生合作交流的能力。
六. 教学准备1.教具准备:课件、黑板、粉笔、练习题等。
2.学具准备:学生每人一本练习册,一盒笔。
七. 教学过程1.导入(5分钟)通过一个现实生活中的情境,如购物场景,展示两位数加一位数的实际问题,引导学生思考如何进行计算。
2.呈现(10分钟)利用课件展示两位数加一位数(不进位)的计算方法,引导学生观察和思考。
通过举例讲解,让学生理解加法运算的原理。
3.操练(10分钟)学生分组进行练习,互相讨论和解答问题。
教师巡回指导,解答学生的疑问,并纠正错误。
4.巩固(10分钟)学生独立完成练习题,教师选取部分题目进行讲解和分析,巩固学生对两位数加一位数(不进位)的计算方法。
5.拓展(10分钟)引导学生思考两位数加一位数(进位)的计算方法,为学生后续学习打下基础。



2.2椭圆课时分配:1.第一课椭圆及其标准方程1个课时2.第二课椭圆的简单几何性质1个课时2.2.1椭圆及其标准方程【教材分析】圆锥曲线被安排在第二章中,以“圆锥曲线与方程”的标题出现,其包含曲线与方程、椭圆、双曲线、抛物线四部分内容。
本节是整个解析几何部分的重要基础知识。
椭圆的定义与初中时学生学习的圆的定义具有相通之处,就是“点动成线”的原理。
通过学习,让学生理解当点运动的规则(遵循的几何关系)发生变化的时候,则画出的曲线的形状也会不同。
高中阶段,在《直线和圆的方程》的学习过程中,学生对坐标法(解析法)思想有了一定程度的认识;在“曲线与方程”和“方程与曲线”的概念中,学生进一步明确了坐标法及其研究曲线的方程的一般步骤。
从本节课开始,又将研究曲线的方法拓展到椭圆,又是继续学习椭圆几何性质的基础,同时还为后面学习双曲线和抛物线作好研究方法和研究思想的准备。
它的学习方法对整个这一章具有导向和引领作用,所以椭圆是学生学习解析几何由浅入深的一个台阶,它在整章中具有承前启后的作用。
【教学目标】知识与技能目标: 1.准确理解椭圆的定义,明确焦点、焦距的概念,掌握椭圆的标准方程及其推导过程;2.根据条件确定椭圆的标准方程;过程与方法目标: 1.通过引导学生亲自动手尝试画图、发现椭圆的形成过程进而归纳出椭圆的定义;在探索椭圆标准方程的过程中,培养学生观察、辨析、归纳和抽象概括问题的能力.2.提高运用坐标法解决几何问题的能力和运算求解和数据处理的能力。
情感态度与价值观目标:通过提炼归纳椭圆的定义的过程,让学生学会将问题抽象成数学问题,并透过运动的现象把握事物的本质;通过经历椭圆方程的化简,增强学生战胜困难的意志品质并体会数学的简洁美、对称美。
通过讨论椭圆方程推导的过程中养成学生扎实严谨的科学态度。
教学重点和难点1.重点:体会椭圆的形成过程,感受求曲线方程的基本方法,掌握椭圆的标准方程及其推导方法。
2.难点:椭圆标准方程的推导(尤其是遇到的根式化简的过程与方法)法与学法(一)教法为了使学生更主动地参与到课堂教学中,体现以学生为主体的探究性学习和因材施教的原则,故采用自主探究法。

教案:《包含分》一、教学内容《包含分》是人教版数学二年级下册第2单元第1节第2课时的内容。
本节课主要引导学生理解包含分的概念,学会用除法计算包含分,并能应用于解决实际问题。
二、教学目标1. 知识与技能:理解包含分的概念,掌握包含分的计算方法,能正确计算包含分。
2. 过程与方法:通过观察、操作、讨论等活动,培养学生的动手操作能力、观察能力和合作交流能力。
3. 情感态度与价值观:激发学生对数学的兴趣,培养良好的学习习惯和团队合作精神。
三、教学难点1. 理解包含分的概念,特别是包含分与平均分的区别。
2. 正确计算包含分,避免出现计算错误。
四、教具学具准备1. 教具:PPT、包含分教具模型、计算器。
2. 学具:练习本、笔。
五、教学过程1. 导入:通过PPT展示一些包含分的图片,引导学生观察并发现其中的规律,引出包含分的概念。
2. 新课导入:教师讲解包含分的概念,并通过教具模型进行演示,让学生直观地理解包含分。
3. 案例分析:教师出示一些包含分的例子,引导学生分析并计算包含分。
4. 实践操作:学生分组进行实践操作,用教具模型计算包含分,加深对包含分的理解。
5. 小结:教师引导学生总结包含分的计算方法,并强调注意事项。
6. 练习:学生独立完成练习题,巩固所学知识。
7. 课堂小结:教师对本节课的内容进行总结,强调重点和难点。
六、板书设计1. 包含分的概念2. 包含分的计算方法3. 包含分与平均分的区别4. 包含分的注意事项七、作业设计1. 完成练习册上的包含分题目。
2. 观察生活中的包含分现象,并尝试用除法计算。
八、课后反思本节课通过观察、操作、讨论等活动,使学生掌握了包含分的概念和计算方法。
但在教学过程中,发现部分学生对包含分与平均分的区别理解不够透彻,需要在今后的教学中加强讲解和练习。
同时,要注重培养学生的动手操作能力和合作交流能力,提高学生的学习兴趣。
重点关注的细节:教学难点在《包含分》这一课时的教学过程中,理解包含分的概念,特别是包含分与平均分的区别,以及正确计算包含分,避免出现计算错误,是学生需要重点掌握的内容。
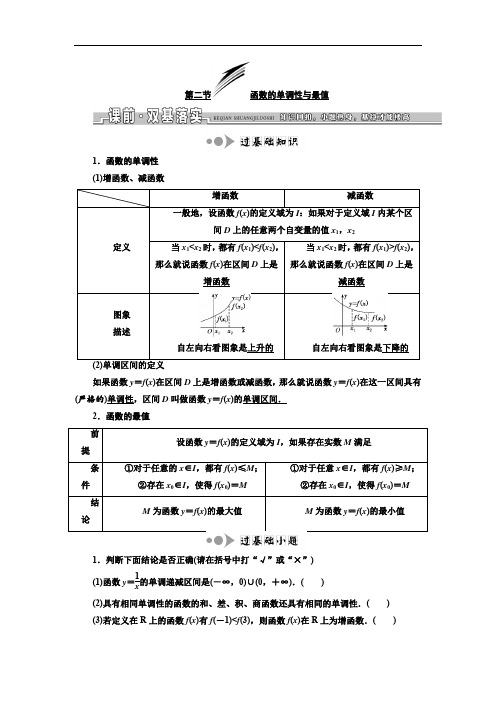
第二节函数的单调性与最值1.函数的单调性(1)增函数、减函数自左向右看图象是上升的自左向右看图象是下降的如果函数y =f (x )在区间D 上是增函数或减函数,那么就说函数y =f (x )在这一区间具有(严格的)单调性,区间D 叫做函数y =f (x )的单调区间.2.函数的最值1.判断下面结论是否正确(请在括号中打“√”或“×”) (1)函数y =1x 的单调递减区间是(-∞,0)∪(0,+∞).( )(2)具有相同单调性的函数的和、差、积、商函数还具有相同的单调性.( ) (3)若定义在R 上的函数f (x )有f (-1)<f (3),则函数f (x )在R 上为增函数.( )(4)函数y =f (x )在[1,+∞)上是增函数,则函数的单调递增区间是[1,+∞).( ) (5)如果一个函数在定义域内的某几个子区间上都是增函数,则这个函数在定义域上是增函数.( )(6)所有的单调函数都有最值.( )答案:(1)× (2)× (3)× (4)× (5)× (6)× 2.下列四个函数中,在(0,+∞)上为增函数的是( ) A .f (x )=3-x B .f (x )=x 2-3x C .f (x )=-1x +1D .f (x )=-|x |解析:选C 当x >0时,f (x )=3-x 为减函数; 当x ∈⎝⎛⎭⎫0,32时,f (x )=x 2-3x 为减函数, 当x ∈⎝⎛⎭⎫32,+∞时,f (x )=x 2-3x 为增函数; 当x ∈(0,+∞)时,f (x )=-1x +1为增函数; 当x ∈(0,+∞)时,f (x )=-|x |为减函数. 3.函数f (x )=|x -2|x 的单调减区间是( ) A .[1,2] B .[-1,0] C .[0,2]D .[2,+∞)解析:选A 由于f (x )=|x -2|x =⎩⎪⎨⎪⎧x 2-2x ,x ≥2,-x 2+2x ,x <2.结合图象(图略)可知函数的单调减区间是[1,2].4.若函数y =x 2-2ax +1在(-∞,2]上是减函数,则实数a 的取值范围是( ) A .(-∞,-2] B .[-2,+∞) C .[2,+∞)D .(-∞,2]解析:选C 函数y =x 2-2ax +1图象的对称轴方程为x =a ,要使该函数在(-∞,2]上是减函数,则需满足a ≥2.5.设定义在[-1,7]上的函数y =f (x )的图象如图所示,则函数y =f (x )的增区间为________.解析:由图可知函数的增区间为[-1,1]和[5,7]. 答案:[-1,1]和[5,7]6.函数f (x )=2x -1在[-2,0]上的最大值与最小值之差为________. 解析:易知f (x )在[-2,0]上是减函数,∴f (x )max -f (x )min =f (-2)-f (0)=-23-(-2)=43.答案:43考点一 确定函数的单调性(区间) (重点保分型考点——师生共研)1.试讨论函数f (x )=axx -1(a ≠0)在(-1,1)上的单调性. 解:法一:设-1<x 1<x 2<1, f (x )=a ⎝ ⎛⎭⎪⎫x -1+1x -1=a ⎝⎛⎭⎫1+1x -1, 则f (x 1)-f (x 2)=a ⎝⎛⎭⎫1+1x 1-1-a ⎝⎛⎭⎫1+1x 2-1=a (x 2-x 1)(x 1-1)(x 2-1).由于-1<x 1<x 2<1,所以x 2-x 1>0,x 1-1<0,x 2-1<0, 故当a >0时,f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 函数f (x )在(-1,1)上单调递减;当a <0时,f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 函数f (x )在(-1,1)上单调递增. 法二:f ′(x )=(ax )′(x -1)-ax (x -1)′(x -1)2=a (x -1)-ax (x -1)2=-a(x -1)2. 当a >0时,f ′(x )<0,函数f (x )在(-1,1)上单调递减; 当a <0时,f ′(x )>0,函数f (x )在(-1,1)上单调递增. 2.求函数f (x )=-x 2+2|x |+1的单调区间.解:易知f (x )=⎩⎪⎨⎪⎧-x 2+2x +1,x ≥0,-x 2-2x +1,x <0=⎩⎪⎨⎪⎧-(x -1)2+2,x ≥0,-(x +1)2+2,x <0. 画出函数图象如图所示,可知单调递增区间为(-∞,-1]和[0,1],单调递减区间为[-1,0]和[1,+∞).[解题师说]1.掌握确定函数单调性(区间)的3种常用方法(1)定义法:一般步骤为设元→作差→变形→判断符号→得出结论.其关键是作差变形,为了便于判断差的符号,通常将差变成因式连乘(除)或平方和的形式,再结合变量的范围、假定的两个自变量的大小关系及不等式的性质进行判断.(如典题领悟第1题)(2)图象法:如果f (x )是以图象形式给出的,或者f (x )的图象易作出,则可由图象的直观性确定它的单调性.(如典题领悟第2题)(3)导数法:利用导数取值的正负确定函数的单调性.(如典题领悟第1题) 2.熟记函数单调性的4个常用结论(1)若f (x ),g (x )均是区间A 上的增(减)函数,则f (x )+g (x )也是区间A 上的增(减)函数; (2)若k >0,则kf (x )与f (x )单调性相同;若k <0,则kf (x )与f (x )单调性相反; (3)函数y =f (x )(f (x )>0)在公共定义域内与y =-f (x ),y =1f (x )的单调性相反; (4)函数y =f (x )(f (x )≥0)在公共定义域内与y =f (x )的单调性相同. 3.谨防3种失误(1)单调区间是定义域的子集,故求单调区间应以“定义域优先”为原则.(如冲关演练第1题)(2)单调区间只能用区间表示,不能用集合或不等式表示.(3)图象不连续的单调区间要分开写,用“和”或“,”连接,不能用“∪”连接.[冲关演练]1.(2017·全国卷Ⅱ)函数f (x )=ln(x 2-2x -8)的单调递增区间是( ) A .(-∞,-2)B .(-∞,1)C .(1,+∞)D .(4,+∞)解析:选D 由x 2-2x -8>0,得x >4或x <-2.因此,函数f (x )=ln(x 2-2x -8)的定义域是(-∞,-2)∪(4,+∞).注意到函数y =x 2-2x -8在(4,+∞)上单调递增,由复合函数的单调性知,f (x )=ln(x 2-2x -8)的单调递增区间是(4,+∞).2.下列函数中,满足“∀x 1,x 2∈(0,+∞)且x 1≠x 2,(x 1-x 2)·[f (x 1)-f (x 2)]<0”的是( ) A .f (x )=2x B .f (x )=|x -1| C .f (x )=1x -xD .f (x )=ln(x +1)解析:选C 由(x 1-x 2)·[f (x 1)-f (x 2)]<0可知,f (x )在(0,+∞)上是减函数,A 、D 选项中,f (x )为增函数;B 中,f (x )=|x -1|在(0,+∞)上不单调,对于f (x )=1x -x ,因为y =1x 与y =-x 在(0,+∞)上单调递减,因此f (x )在(0,+∞)上是减函数.3.已知函数y =1x -1,那么( ) A .函数的单调递减区间为(-∞,1)和(1,+∞) B .函数的单调递减区间为(-∞,1)∪(1,+∞) C .函数的单调递增区间为(-∞,1)和(1,+∞) D .函数的单调递增区间为(-∞,1)∪(1,+∞) 解析:选A 函数y =1x -1可看作是由y =1x 向右平移1个单位长度得到的,∵y =1x 在(-∞,0)和(0,+∞)上单调递减,∴y =1x -1在(-∞,1)和(1,+∞)上单调递减,∴函数y =1x -1的单调递减区间为(-∞,1)和(1,+∞),故选A. 4.判断函数f (x )=x +ax (a >0)在(0,+∞)上的单调性. 解:设x 1,x 2是任意两个正数,且x 1<x 2,则f (x 1)-f (x 2)=⎝⎛⎭⎫x 1+a x 1-⎝⎛⎭⎫x 2+ax 2=x 1-x 2x 1x 2(x 1x 2-a ). 当0<x 1<x 2≤a 时,0<x 1x 2<a ,x 1-x 2<0, 所以f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 所以函数f (x )在(0,a ]上是减函数; 当a ≤x 1<x 2时,x 1x 2>a ,x 1-x 2<0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以函数f (x )在[a ,+∞)上是增函数.综上可知,函数f (x )=x +ax (a >0)在(0,a ]上是减函数,在[a ,+∞)上是增函数. 考点二 求函数的值域(最值) (基础送分型考点——自主练透)[考什么·怎么考]1.函数y =x 2-1x 2+1的值域为________.解析:由y =x 2-1x 2+1,可得x 2=1+y1-y .由x 2≥0,知1+y1-y ≥0,解得-1≤y <1,故所求函数的值域为[-1,1). 答案:[-1,1)2.若函数f (x )=-ax +b (a >0)在⎣⎡⎦⎤12,2上的值域为⎣⎡⎦⎤12,2,则a =________,b =________. 解析:∵f (x )=-ax +b (a >0)在⎣⎡⎦⎤12,2上是增函数, ∴f (x )min =f ⎝⎛⎭⎫12=12,f (x )max =f (2)=2.即⎩⎨⎧-2a +b =12,-a2+b =2,解得a =1,b =52.答案:152[方法点拨](1)先进行转化与分离,再利用函数的性质(如x 2≥0,e x >0等)求解即可.(2)如果函数y =f (x )在区间[a ,b ]上单调递增,那么f (x )在区间端点处取最值;如果函数y =f (x )在区间[a ,b ]上单调递增,在区间[b ,c ]上单调递减,那么y max =f (b );如果函数y =f (x )在区间[a ,b ]上单调递减,在区间[b ,c ]上单调递增,那么y min =f (b ),从而得出值域.方法(二) 数形结合法求函数的值域(最值) 3.函数y =|x +1|+|x -2|的值域为________. 解析:函数y =⎩⎪⎨⎪⎧-2x +1,x ≤-1,3,-1<x <2,2x -1,x ≥2.作出函数的图象如图所示.根据图象可知,函数y =|x +1|+|x -2|的值域为[3,+∞). 答案:[3,+∞)4.设函数f (x )=⎩⎪⎨⎪⎧m +x 2,|x |≥1,x ,|x |<1的图象过点(1,1),函数g (x )是二次函数,若函数f (g (x ))的值域是[0,+∞),则函数g (x )的值域是________.解析:因为函数f (x )=⎩⎪⎨⎪⎧m +x 2,|x |≥1,x ,|x |<1的图象过点(1,1),所以m +1=1,解得m =0,所以f (x )=⎩⎪⎨⎪⎧x 2,|x |≥1,x ,|x |<1.画出函数y =f (x )的大致图象如图所示,观察图象可知,当纵坐标在[0,+∞)上时,横坐标在(-∞,-1]∪[0,+∞)上变化.而f (x )的值域为[-1,+∞),f (g (x ))的值域为[0,+∞),因为g (x )是二次函数, 所以g (x )的值域是[0,+∞). 答案:[0,+∞) [方法点拨]先作出函数的图象,再观察其最高点或最低点,求出值域或最值. 方法(三) 换元法求函数的值域(最值) 5.函数y =x +1-x 2的最大值为________. 解析:由1-x 2≥0,可得-1≤x ≤1. 可令x =cos θ,θ∈[0,π],则y =cos θ+sin θ=2sin ⎝⎛⎭⎫θ+π4,θ∈[]0,π, 所以-1≤y ≤2,故原函数的最大值为 2. 答案:[2]6.已知函数f (x )的值域为⎣⎡⎦⎤38,49,则函数g (x )=f (x )+1-2f (x )的值域为________. 解析:∵38≤f (x )≤49,∴13≤1-2f (x )≤12. 令t =1-2f (x ),则f (x )=12(1-t 2)⎝⎛⎭⎫13≤t ≤12, 令y =g (x ),则y =12(1-t 2)+t ,即y =-12(t -1)2+1⎝⎛⎭⎫13≤t ≤12. ∴当t =13时,y 有最小值79;当t =12时,y 有最大值78.∴g (x )的值域为⎣⎡⎦⎤79,78. 答案:⎣⎡⎦⎤79,78 [方法点拨]对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求值域或最值;换元法求值域时,一定要注意新元的范围对值域的影响.方法(四) 分离常数法求函数的值域(最值) 7.函数y =3x +1x -2的值域为________. 解析:y =3x +1x -2=3(x -2)+7x -2=3+7x -2,因为7x -2≠0,所以3+7x -2≠3, 所以函数y =3x +1x -2的值域为{y |y ∈R 且y ≠3}. 答案:{y |y ∈R 且y ≠3}8.当-3≤x ≤-1时,函数y =5x -14x +2的最小值为________.解析:由y =5x -14x +2,可得y =54-74(2x +1).∵-3≤x ≤-1,∴720≤-74(2x +1)≤74,∴85≤y ≤3 ∴所求函数的最小值为85答案:85[方法点拨]通过配凑函数解析式的分子,把函数分离成常数和分式的形式,而此式的分式,只有分母中含有变量,进而可利用函数性质确定其值域.[怎样快解·准解]求函数值域(最值)的类型及其方法(1)若所给函数为单调函数,可根据函数的单调性求值域;当函数解析式中出现偶次方幂、绝对值等时,可利用函数的性质(如x 2≥0,|x |≥0,x ≥0,e x >0等)确定函数的值域或最值.(2)若函数解析式的几何意义较明显(如距离、斜率等)或函数图象易作出,可用数形结合法求函数的值域或最值.(3)形如求y =ax +b +(cx +d )(ac ≠0)的函数的值域或最值,常用代数换元法、三角换元法结合题目条件将原函数转化为熟悉的函数,再利用函数的相关性质求解.(4)形如求y =cx +dax +b(ac ≠0)的函数的值域或最值常用分离常数法求解. 另外,基本不等式法、导数法求函数值域或最值也是常用方法,在后面章节中有重点讲述.考点三 函数单调性的应用 (题点多变型考点——追根溯源)角度(一) 比较函数值的大小1.(2018·哈尔滨联考)已知函数f (x )的图象关于直线x =1对称,当x 2>x 1>1时,[f (x 2)-f (x 1)](x 2-x 1)<0恒成立,设a =f ⎝⎛⎭⎫-12,b =f (2),c =f (e),则a ,b ,c 的大小关系为( ) A .c >a >b B .c >b >a C .a >c >bD .b >a >c解析:选D 因为f (x )的图象关于直线x =1对称,所以f ⎝⎛⎭⎫-12=f ⎝⎛⎭⎫52.由x 2>x 1>1时,[f (x 2)-f (x 1)]·(x 2-x 1)<0恒成立,知f (x )在(1,+∞)上单调递减.∵1<2<52<e ,∴f (2)>f ⎝⎛⎭⎫52>f (e), ∴b >a >c .[题型技法] 比较函数值大小的解题思路比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用其函数性质,转化到同一个单调区间上进行比较,对于选择题、填空题能数形结合的尽量用图象法求解.角度(二) 解函数不等式2.定义在R 上的奇函数y =f (x )在(0,+∞)上递增,且f ⎝⎛⎭⎫12=0,则不等式f (log 19x )>0的解集为________.解析:∵y =f (x )是定义在R 上的奇函数,且y =f (x )在(0,+∞)上递增. ∴y =f (x )在(-∞,0)上也是增函数, 又f ⎝⎛⎭⎫12=0,知f ⎝⎛⎭⎫-12=-f ⎝⎛⎭⎫12=0. 故原不等式f (log 19x )>0可化为f (log 19x )>f ⎝⎛⎭⎫12或f ⎝⎛⎭⎫-12<f (log 19x )<f ()0, ∴log 19x >12或-12<log 19x <0,解得0<x <13或1<x <3.所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪0<x <13或1<x <3. 答案:⎩⎨⎧⎭⎬⎫x ⎪⎪0<x <13或1<x <3[题型技法] 求解含“f ”的函数不等式的解题思路先利用函数的相关性质将不等式转化为f (g (x ))>f (h (x ))的形式,再根据函数的单调性去掉“f ”,得到一般的不等式g (x )>h (x )(或g (x )<h (x )).角度(三) 利用单调性求参数的取值范围(或值)3.已知函数f (x )=⎩⎪⎨⎪⎧ax 2-x -14,x ≤1,log a x -1,x >1是R 上的单调函数,则实数a 的取值范围是( )A.⎣⎡⎭⎫14,12 B.⎣⎡⎦⎤14,12 C.⎝⎛⎦⎤0,12 D.⎣⎡⎭⎫12,1解析:选B 由对数函数的定义可得a >0,且a ≠1.又函数f (x )在R 上单调,而二次函数y =ax 2-x -14的图象开口向上,所以函数f (x )在R 上单调递减, 故有⎩⎪⎨⎪⎧0<a <1,12a≥1,a ×12-1-14≥log a1-1,即⎩⎪⎨⎪⎧0<a <1,0<a ≤12,a ≥14.所以a ∈⎣⎡⎦⎤14,12.[题型技法] 利用单调性求参数的范围(或值)的方法(1)视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数;(2)需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的.[题“根”探求]对于求解此类有关函数单调性应用的题目,其通用的方法是利用转化思想解题,其思维流程是:1.已知函数f (x )是定义在(0,+∞)上的增函数,若f (a 2-a )>f (a +3),则实数a 的取值范围为________.解析:由已知可得⎩⎪⎨⎪⎧a 2-a >0,a +3>0,a 2-a >a +3,解得-3<a <-1或a >3,所以实数a 的取值范围为(-3,-1)∪(3,+∞).答案:(-3,-1)∪(3,+∞)2.已知函数f (x )=x |2x -a |(a >0)在区间[2,4]上单调递减,则实数a 的值是________.解析:f (x )=x |2x -a |=⎩⎨⎧x (2x -a ),x >a 2,-x (2x -a ),x ≤a2(a >0),作出函数图象(图略)可得该函数的递减区间是⎣⎡⎦⎤a 4,a2,所以⎩⎨⎧a4≤2,a2≥4,解得a =8.答案:8(一)普通高中适用作业A 级——基础小题练熟练快1.下列函数中,在区间(0,+∞)上为增函数的是( ) A .y =ln(x +2) B .y =-x +1 C .y =⎝⎛⎭⎫12xD .y =x +1x解析:选A 函数y =ln(x +2)的增区间为(-2,+∞),所以在(0,+∞)上一定是增函数.2.如果函数f (x )=ax 2+2x -3在区间(-∞,4)上是单调递增的,则实数a 的取值范围是( )A.⎝⎛⎭⎫-14,+∞B.⎣⎡⎭⎫-14,+∞ C.⎣⎡⎭⎫-14,0 D.⎣⎡⎦⎤-14,0 解析:选D 当a =0时,f (x )=2x -3在定义域R 上是单调递增的,故在(-∞,4)上单调递增;当a ≠0时,二次函数f (x )的对称轴为x =-1a , 因为f (x )在(-∞,4)上单调递增, 所以a <0,且-1a ≥4,解得-14≤a <0.综上,实数a 的取值范围是⎣⎡⎦⎤-14,0. 3.已知函数f (x )是定义在区间[0,+∞)上的函数,且在该区间上单调递增,则满足f (2x -1)<f ⎝⎛⎭⎫13的x 的取值范围是( )A.⎝⎛⎭⎫13,23 B.⎣⎡⎭⎫13,23 C.⎝⎛⎭⎫12,23D.⎣⎡⎭⎫12,23解析:选D 因为函数f (x )是定义在区间[0,+∞)上的增函数,满足f (2x -1)<f ⎝⎛⎭⎫13. 所以0≤2x -1<13,解得12≤x <23.4.函数y =|x |(1-x )在区间A 上是增函数,那么区间A 是( ) A .(-∞,0)B.⎣⎡⎦⎤0,12C .[0,+∞)D.⎝⎛⎭⎫12,+∞ 解析:选B y =|x |(1-x )=⎩⎪⎨⎪⎧x (1-x ),x ≥0,-x (1-x ),x <0, =⎩⎪⎨⎪⎧-x 2+x ,x ≥0,x 2-x ,x <0, =⎩⎨⎧-⎝⎛⎭⎫x -122+14,x ≥0,⎝⎛⎭⎫x -122-14,x <0.画出函数的大致图象如图所示. 由图易知原函数在⎣⎡⎦⎤0,12上单调递增. 5.设偶函数f (x )的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则f (-2),f (π),f (-3)的大小关系是( )A .f (π)>f (-3)>f (-2)B .f (π)>f (-2)>f (-3)C .f (π)<f (-3)<f (-2)D .f (π)<f (-2)<f (-3)解析:选A 因为f (x )是偶函数, 所以f (-3)=f (3),f (-2)=f (2). 又因为函数f (x )在[0,+∞)上是增函数, 所以f (π)>f (3)>f (2), 即f (π)>f (-3)>f (-2). 6.已知函数f (x )=log 2x +11-x,若x 1∈(1,2),x 2∈(2,+∞),则( ) A .f (x 1)<0,f (x 2)<0 B .f (x 1)<0,f (x 2)>0 C .f (x 1)>0,f (x 2)<0D .f (x 1)>0,f (x 2)>0解析:选B ∵函数f (x )=log 2x +11-x 在(1,+∞)上为增函数,且f (2)=0,∴当x 1∈(1,2)时,f (x 1)<f (2)=0;当x 2∈(2,+∞)时,f (x 2)>f (2)=0,即f (x 1)<0,f (x 2)>0.7.函数f (x )=⎩⎪⎨⎪⎧1x ,x ≥1,-x 2+2,x <1的最大值为________.解析:当x ≥1时,函数f (x )=1x 为减函数,所以f (x )在x =1处取得最大值,为f (1)=1;当x <1时,易知函数f (x )=-x 2+2在x =0处取得最大值,为f (0)=2.故函数f (x )的最大值为2.答案:28.已知函数f (x )=x 2-2x -3,则该函数的单调递增区间为________.解析:设t =x 2-2x -3,由t ≥0,即x 2-2x -3≥0,解得x ≤-1或x ≥3,所以函数f (x )的定义域为(-∞,-1]∪[3,+∞).因为函数t =x 2-2x -3的图象的对称轴为x =1,所以函数t 在(-∞,-1]上单调递减,在[3,+∞)上单调递增,所以函数f (x )的单调递增区间为[3,+∞).答案:[3,+∞)9.若函数f (x )=1x 在区间[2,a ]上的最大值与最小值的和为34,则a =________.解析:由f (x )=1x 的图象知,f (x )=1x 在(0,+∞)上是减函数,∵[2,a ]⊆(0,+∞),∴f (x )=1x 在[2,a ]上也是减函数, ∴f (x )max =f (2)=12,f (x )min =f (a )=1a ,∴12+1a =34,∴a =4. 答案:410.给定函数:①y =x 12;②y =log 12(x +1);③y =|x -1|;④y =2x +1,其中在区间(0,1)上单调递减的函数序号是________.解析:①y =x 12在(0,1)上递增;②因为t =x +1在(0,1)上递增,且0<12<1,故y =log 12(x+1)在(0,1)上递减;③结合函数图象可知y =|x -1|在(0,1)上递减;④因为u =x +1在(0,1)上递增,且2>1,故y =2x+1在(0,1)上递增,故在区间(0,1)上单调递减的函数序号是②③.答案:②③B 级——中档题目练通抓牢1.若函数f (x )=x 2+a |x |+2,x ∈R 在区间[3,+∞)和[-2,-1]上均为增函数,则实数a 的取值范围是( )A.⎣⎡⎦⎤-113,-3 B .[-6,-4] C.[]-3,-22D.[]-4,-3解析:选B 由于f (x )为R 上的偶函数,因此只需考虑函数f (x )在(0,+∞)上的单调性即可.由题意知函数f (x )在[3,+∞)上为增函数,在[1,2]上为减函数,故-a2∈[2,3],即a∈[-6,-4].2.已知函数f (x )是R 上的增函数,A (0,-3),B (3,1)是其图象上的两点,那么不等式-3<f (x +1)<1的解集的补集是(全集为R)( )A .(-1,2)B .(1,4)C .(-∞,-1)∪[4,+∞)D .(-∞,-1]∪[2,+∞)解析:选D 由函数f (x )是R 上的增函数,A (0,-3),B (3,1)是其图象上的两点,知不等式-3<f (x +1)<1即为f (0)<f (x +1)<f (3),所以0<x +1<3,所以-1<x <2,故不等式-3<f (x +1)<1的解集的补集是(-∞,-1]∪[2,+∞).3.(2018·河南平顶山一模)已知f (x )是定义在(0,+∞)上的函数.对任意两个不相等的正数x 1,x 2,都有x 2f (x 1)-x 1f (x 2)x 1-x 2>0,记a =f (30.2)30.2,b =f (0.32)0.32,c =f (log 25)log 25,则a ,b ,c 的大小关系为( )A .a <b <cB .b <a <cC .c <a <bD .c <b <a解析:选B 对任意两个不相等的正数x 1,x 2,不妨设x 1>x 2, ∵x 2f (x 1)-x 1f (x 2)x 1-x 2>0,∴x 2f (x 1)-x 1f (x 2)>0, ∴x 2f (x 1)-x 1f (x 2)x 1x 2=f (x 1)x 1-f (x 2)x 2>0,即f (x 1)x 1>f (x 2)x 2, ∴f (x )x是(0,+∞)上的增函数. ∵1<30.2<30.5<2,0<0.32<1,log 25>2, ∴0.32<30.2<log 25, ∴b <a <c .4.设函数f (x )=⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0,g (x )=x 2f (x -1),则函数g (x )的递减区间是________.解析:由题意知g (x )=⎩⎪⎨⎪⎧x 2,x >1,0,x =1,-x 2,x <1.作出函数图象如图所示,其递减区间是[0,1). 答案:[0,1) 5.若函数y =2x +kx -2与y =log 3(x -2)在(3,+∞)上具有相同的单调性,则实数k 的取值范围是____________.解析:由于y =log 3(x -2)在(3,+∞)上为增函数,故函数y =2x +k x -2=2(x -2)+4+kx -2=2+4+k x -2在(3,+∞)上也是增函数,则有4+k <0,得k <-4. 答案:(-∞,-4)6.已知函数f (x )=1a -1x (a >0,x >0).(1)求证:f (x )在(0,+∞)上是增函数;(2)若f (x )在⎣⎡⎦⎤12,2上的值域是⎣⎡⎦⎤12,2,求a 的值. 解:(1)证明:任取x 1>x 2>0, 则f (x 1)-f (x 2)=1a -1x 1-1a +1x 2=x 1-x 2x 1x 2,∵x 1>x 2>0,∴x 1-x 2>0,x 1x 2>0, ∴f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2),∴f (x )在(0,+∞)上是增函数.(2)由(1)可知,f (x )在⎣⎡⎦⎤12,2上为增函数, ∴f ⎝⎛⎭⎫12=1a -2=12, f (2)=1a -12=2,解得a =25.7.已知f (x )=xx -a(x ≠a ). (1)若a =-2,试证f (x )在(-∞,-2)内单调递增;(2)若a >0且f (x )在(1,+∞)内单调递减,求a 的取值范围.解:(1)证明:当a =-2时,f (x )=x x +2. 任取x 1,x 2∈(-∞,-2),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=2(x 1-x 2)(x 1+2)(x 2+2). 因为(x 1+2)(x 2+2)>0,x 1-x 2<0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )在(-∞,-2)内单调递增. (2)任取x 1,x 2∈(1,+∞),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a =a (x 2-x 1)(x 1-a )(x 2-a ). 因为a >0,x 2-x 1>0,又由题意知f (x 1)-f (x 2)>0, 所以(x 1-a )(x 2-a )>0恒成立,所以a ≤1. 所以0<a ≤1.所以a 的取值范围为(0,1]. C 级——重难题目自主选做1.已知函数f (x )=⎩⎪⎨⎪⎧x 3,x ≤0,ln (x +1),x >0,若f (2-x 2)>f (x ),则实数x 的取值范围是( )A .(-∞,-1)∪(2,+∞)B .(-∞,-2)∪(1,+∞)C .(-1,2)D .(-2,1)解析:选D ∵当x =0时,两个表达式对应的函数值都为0,∴函数的图象是一条连续的曲线.又∵当x ≤0时,函数f (x )=x 3为增函数,当x >0时,f (x )=ln(x +1)也是增函数,∴函数f (x )是定义在R 上的增函数.因此,不等式f (2-x 2)>f (x )等价于2-x 2>x ,即x 2+x -2<0,解得-2<x <1.2.如果函数y =f (x )在区间I 上是增函数,且函数y =f (x )x 在区间I 上是减函数,那么称函数y =f (x )是区间I 上的“缓增函数”,区间I 叫做“缓增区间”.若函数f (x )=12x 2-x +32是区间I 上的“缓增函数”,则“缓增区间”I 为( ) A .[1,+∞) B .[0, 3 ] C .[0,1]D .[1, 3 ]解析:选D 因为函数f (x )=12x 2-x +32的对称轴为x =1,所以函数y =f (x )在区间[1,+∞)上是增函数,又当x ≥1时,f (x )x =12x +32x -1,令g (x )=12x +32x-1(x ≥1),则g ′(x )=12-32x 2=x 2-32x 2,由g ′(x )≤0,得1≤x ≤3,即函数f (x )x =12x -1+32x在区间[1, 3 ]上单调递减,故“缓增区间”I 为[1, 3 ].(二)重点高中适用作业A 级——保分题目巧做快做1.下列函数中,在区间(0,+∞)上为增函数的是( ) A .y =ln(x +2) B .y =-x +1 C .y =⎝⎛⎭⎫12xD .y =x +1x解析:选A 函数y =ln(x +2)的增区间为(-2,+∞),所以在(0,+∞)上一定是增函数.2.已知函数f (x )=x 2-2x -3,则该函数的单调递增区间为( ) A .(-∞,1] B .[3,+∞) C .(-∞,-1]D .[1,+∞)解析:选B 设t =x 2-2x -3,由t ≥0,即x 2-2x -3≥0,解得x ≤-1或x ≥3,所以函数f (x )的定义域为(-∞,-1]∪[3,+∞).因为函数t =x 2-2x -3的图象的对称轴为x =1,所以函数t 在(-∞,-1]上单调递减,在[3,+∞)上单调递增,所以函数f (x )的单调递增区间为[3,+∞).3.设偶函数f (x )的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则f (-2),f (π),f (-3)的大小关系是( )A .f (π)>f (-3)>f (-2)B .f (π)>f (-2)>f (-3)C .f (π)<f (-3)<f (-2)D .f (π)<f (-2)<f (-3)解析:选A 因为f (x )是偶函数, 所以f (-3)=f (3),f (-2)=f (2). 又因为函数f (x )在[0,+∞)上是增函数, 所以f (π)>f (3)>f (2), 即f (π)>f (-3)>f (-2).4.已知定义在R 上的奇函数f (x )在[0,+∞)上单调递减,若f (x 2-2x +a )<f (x +1)对任意的x ∈[-1,2]恒成立,则实数a 的取值范围为( )A.⎝⎛⎭⎫-∞,134 B .(-∞,-3)C .(-3,+∞)D.⎝⎛⎭⎫134,+∞ 解析:选D 依题意得f (x )在R 上是减函数,所以f (x 2-2x +a )<f (x +1)对任意的x ∈[-1,2]恒成立,等价于x 2-2x +a >x +1对任意的x ∈[-1,2]恒成立,等价于a >-x 2+3x +1对任意的x ∈[-1,2]恒成立.设g (x )=-x 2+3x +1(-1≤x ≤2),则g (x )=-⎝⎛⎭⎫x -322+134(-1≤x ≤2),当x =32时,g (x )取得最大值,且g (x )max =g ⎝⎛⎭⎫32=134,因此a >134,故选D. 5.定义新运算⊕:当a ≥b 时,a ⊕b =a ;当a <b 时,a ⊕b =b 2,则函数f (x )=(1⊕x )x -(2⊕x ),x ∈[-2,2]的最大值等于( )A .-1B .1C .6D .12解析:选C 由已知得当-2≤x ≤1时,f (x )=x -2, 当1<x ≤2时,f (x )=x 3-2.因为f (x )=x 3-2,f (x )=x -2在定义域内都为增函数, 且f (1)<f (2),所以f (x )的最大值为f (2)=23-2=6.6.(2018·安徽合肥模拟)已知函数f (x )=(x 2-2x )sin(x -1)+x +1在[-1,3]上的最大值为M ,最小值为m ,则M +m =________.解析:由f (x )=(x 2-2x )sin(x -1)+x +1令t =x -1,则t ∈[-2,2],则y =(t 2-1)sin t +t +2,t ∈[-2,2].记g (t )=(t 2-1)sin t +t +2,则函数y =g (t )-2=(t 2-1)sin t +t 是奇函数.由已知得y =g (t )-2的最大值为M -2,最小值为m -2,所以M -2+(m -2)=0,即M +m =4.答案:47.已知函数f (x )=⎩⎪⎨⎪⎧e x-k ,x ≤0,(1-k )x +k ,x >0是R 上的增函数,则实数k 的取值范围是________.解析:由题意得⎩⎪⎨⎪⎧e 0-k ≤k ,1-k >0,解得12≤k <1.答案:⎣⎡⎭⎫12,1 8.若函数y =2x +kx -2与y =log 3(x -2)在(3,+∞)上具有相同的单调性,则实数k 的取值范围是____________.解析:由于y =log 3(x -2)在(3,+∞)上为增函数,故函数y =2x +k x -2=2(x -2)+4+kx -2=2+4+k x -2在(3,+∞)上也是增函数,则有4+k <0,得k <-4.答案:(-∞,-4)9.已知函数f (x )=1a -1x (a >0,x >0). (1)求证:f (x )在(0,+∞)上是增函数;(2)若f (x )在⎣⎡⎦⎤12,2上的值域是⎣⎡⎦⎤12,2,求a 的值. 解:(1)证明:任取x 1>x 2>0, 则f (x 1)-f (x 2)=1a -1x 1-1a +1x 2=x 1-x 2x 1x 2,∵x 1>x 2>0,∴x 1-x 2>0,x 1x 2>0, ∴f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), ∴f (x )在(0,+∞)上是增函数.(2)由(1)可知,f (x )在⎣⎡⎦⎤12,2上为增函数, ∴f ⎝⎛⎭⎫12=1a -2=12, f (2)=1a -12=2,解得a =25.10.已知f (x )=xx -a(x ≠a ). (1)若a =-2,试证f (x )在(-∞,-2)内单调递增;(2)若a >0且f (x )在(1,+∞)内单调递减,求a 的取值范围. 解:(1)证明:当a =-2时,f (x )=x x +2. 任取x 1,x 2∈(-∞,-2),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=2(x 1-x 2)(x 1+2)(x 2+2). 因为(x 1+2)(x 2+2)>0,x 1-x 2<0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )在(-∞,-2)内单调递增. (2)任取x 1,x 2∈(1,+∞),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a =a (x 2-x 1)(x 1-a )(x 2-a ). 因为a >0,x 2-x 1>0,又由题意知f (x 1)-f (x 2)>0, 所以(x 1-a )(x 2-a )>0恒成立,所以a ≤1. 所以0<a ≤1.所以a 的取值范围为(0,1]. B 级——拔高题目稳做准做1.函数y =f (x )(x ∈R)的图象如图所示,则函数g (x )=f (log a x )(0<a <1)的单调递减区间是( )A.⎣⎡⎦⎤0,12 B .[a ,1] C .(-∞,0)∪⎣⎡⎭⎫12,+∞ D .[a ,a +1 ]解析:选B 由图象知f (x )在(-∞,0]和⎣⎡⎭⎫12,+∞上单调递减,而在⎣⎡⎦⎤0,12上单调递增.又因为当0<a <1时,y =log a x 为(0,+∞)上的减函数,所以要使g (x )=f (log a x )单调递减,则需log a x ∈⎣⎡⎦⎤0,12,即0≤log a x ≤12, 解得x ∈[a ,1].2.如果函数y =f (x )在区间I 上是增函数,且函数y =f (x )x 在区间I 上是减函数,那么称函数y =f (x )是区间I 上的“缓增函数”,区间I 叫做“缓增区间”.若函数f (x )=12x 2-x +32是区间I 上的“缓增函数”,则“缓增区间”I 为( ) A .[1,+∞)B .[0, 3 ]C .[0,1]D .[1, 3 ]解析:选D 因为函数f (x )=12x 2-x +32的对称轴为x =1,所以函数y =f (x )在区间[1,+∞)上是增函数,又当x ≥1时,f (x )x =12x +32x -1,令g (x )=12x +32x-1(x ≥1),则g ′(x )=12-32x 2=x 2-32x 2,由g ′(x )≤0得1≤x ≤3,即函数f (x )x =12x -1+32x在区间[1, 3 ]上单调递减,故“缓增区间”I 为[1, 3 ].3.设函数f (x )=⎩⎪⎨⎪⎧ 1,x >0,0,x =0,-1,x <0,g (x )=x 2f (x -1),则函数g (x )的递减区间是________.解析:由题意知g (x )=⎩⎪⎨⎪⎧ x 2,x >1,0,x =1,-x 2,x <1.作出函数图象如图所示,则其递减区间是[0,1).答案:[0,1)4.已知函数f (x )=⎩⎪⎨⎪⎧x 2-4x +5,x ≤2,log 12(x -1)+1,x >2,若f (a 2-3a )>f (2a -6),则实数a 的取值范围是________.解析:因为f 1(x )=x 2-4x +5在(-∞,2]上为减函数,f 2(x )=log 12(x -1)+1在(2,+∞)上为减函数. 又f 1(2)=f 2(2)=1,所以函数f (x )在R 上为单调递减函数,所以f (a 2-3a )>f (2a -6),则a 2-3a <2a -6⇒a 2-5a +6<0,解得2<a <3.答案:(2,3)5.已知函数f (x )=2x -a x 的定义域为(0,1](a 为实数).(1)当a =1时,求函数y =f (x )的值域;(2)求函数y =f (x )在区间(0,1]上的最大值及最小值,并求当函数f (x )取得最值时x 的值.解:(1)当a =1时,f (x )=2x -1x ,任取0<x 2<x 1≤1,则f (x 1)-f (x 2)=2(x 1-x 2)-⎝⎛⎭⎫1x 1-1x 2 =(x 1-x 2)⎝⎛⎭⎫2+1x 1x 2.∵0<x 2<x 1≤1,∴x 1-x 2>0,x 1x 2>0.∴f (x 1)>f (x 2),∴f (x )在(0,1]上单调递增,当x =1时取得最大值1,∴f (x )的值域为(-∞,1].(2)当a ≥0时,y =f (x )在(0,1]上单调递增,无最小值,当x =1时取得最大值2-a ;当a <0时,f (x )=2x +-a x ,当 -a 2≥1,即a ∈(-∞,-2]时,y =f (x )在(0,1]上单调递减,无最大值,当x =1时取得最小值2-a ;当 -a 2<1,即a ∈(-2,0)时,y =f (x )在⎝⎛⎦⎤0, -a 2上单调递减,在⎣⎡⎦⎤ -a 2,1上单调递增,无最大值,当x = -a 2时取得最小值2-2a . 6.已知定义在区间(0,+∞)上的函数f (x )满足f ⎝⎛⎭⎫x 1x 2=f (x 1)-f (x 2),且当x >1时,f (x )<0.(1)证明:f (x )为单调递减函数.(2)若f (3)=-1,求f (x )在[2,9]上的最小值.解:(1)证明:任取x 1,x 2∈(0,+∞),且x 1>x 2,则x 1x 2>1,由于当x >1时,f (x )<0, 所以f ⎝⎛⎭⎫x 1x 2<0,即f (x 1)-f (x 2)<0, 因此f (x 1)<f (x 2),所以函数f (x )在区间(0,+∞)上是单调递减函数.(2)因为f (x )在(0,+∞)上是单调递减函数,所以f (x )在[2,9]上的最小值为f (9). 由f ⎝⎛⎭⎫x 1x 2=f (x 1)-f (x 2)得,f ⎝⎛⎭⎫93=f (9)-f (3),而f (3)=-1,所以f (9)=-2.所以f (x )在[2,9]上的最小值为-2. 古今中外有学问的人,有成就的人,总是十分注意积累的。

高二数学 第二章 第1节椭圆(文) 北师大版选修1—1【本讲教育信息】一. 教学内容:选修1—1第二章椭圆的标准方程及几何性质 二. 教学目标:1. 熟练的掌握椭圆的定义及标准方程的形式,能根据已知条件求出椭圆的标准方程。
2. 掌握椭圆简单的几何性质,会求椭圆的准线、离心率、焦点坐标。
3. 理解用方程的思想、函数的思想、数与形结合、分类讨论的思想及定义法、待定系数法等数学思想方法解决椭圆的有关问题。
三. 知识要点分析: (一)椭圆的基本概念椭圆的定义:1. 椭圆的第一定义:平面内到两个定点F 1,F 2的距离之和等于常数(大于|F 1F 2|)的点的集合叫椭圆。
点集M={P| |PF 1|+|PF 2|=2a ,2a>|F 1F 2|}。
(1)到两个定点F 1,F 2的距离之和等于|F 1F 2|的点的集合是线段F 1F 2. (2)到两个定点F 1,F 2的距离之和小于|F 1F 2|的点的集合是空集。
2.椭圆的第二定义:平面内一动点到一个定点和一条定直线的距离的比是小于1的正常数的点的集合叫椭圆。
点集M={P|}10,||1<<=e e dPF 椭圆的标准方程的两种形式:)0(,12222>>=+b a b y a x (焦点在x 轴上),22221).0,(),0,(c b a c F c F =-- )0(,12222>>=+b a a y b x (焦点在y 轴上),22221).,0(),,0(c b a c F c F =-- 点与椭圆的位置关系1by a x )0b a (1b y a x )y ,x (P 220220222200<+⇔>>=+内部在椭圆1by a x )0b a (1b y a x )y ,x (P 22220222200=+⇔>>=+上在椭圆1b y a x )0b a (1b y a x )y ,x (P 22022222200>+⇔>>=+外部在椭圆焦点在x 轴上焦点在y 轴上图形性 质X 围|x|≤a ,|y|≤b|x|≤b ,|y|≤a对称性关于x 轴、y 轴、坐标原点对称顶点 A 1(-a ,0) A 2(a ,0) B 1(0,-b ) B 2(0,b )A 1(0,-a ) A 2(0,a )B 1(-b ,0) B 2(b ,0)离心率 离心率e=ac,0<e<1,(焦距与长轴的比)(对椭圆定型) 准线 x=ca 2±y=ca 2±焦点半径公式|0201||,|ex a PF ex a PF -=+=|0201||,|ey a PF ey a PF -=+=注:1.在确定椭圆的标准方程时若不能确定焦点的位置,可讨论焦点在x 轴上、y 轴上两种情形或把所求的椭圆标准方程设为:),0,0(,122B A B A By Ax ≠>>=+ .2. 与椭圆)0(,12222>>=+b a b y a x 共焦点的椭圆可设为:kb y k a x +++2222 =1,(a>0,b>0)3. 椭圆上任意一点P 到焦点F 的距离最大值是|PF|=a+c ,最小值是|PF|=a -c 。
