概率论与数理统计基础知识网络结构图

高校统计学专业概率论知识点整理思维导图概率论是统计学中重要的基础学科，它研究的是不确定事件的数量关系和规律性。

对于高校统计学专业的学生来说，掌握概率论知识是非常重要的。

本文将通过整理概率论的知识点，并以思维导图的形式展示，帮助读者更好地理解和记忆。

一、概率基本概念1. 随机试验- 随机试验的定义- 试验的分类- 样本空间和样本点2. 事件与事件的关系- 事件的定义- 事件的运算- 事件关系的性质3. 概率的定义与性质- 古典概型- 几何概型- 组合概型二、概率分布1. 随机变量- 随机变量的定义- 随机变量的分类- 随机变量的分布函数2. 离散型随机变量及其分布- 离散型随机变量的定义- 二项分布、泊松分布等常见分布 - 离散型随机变量的期望和方差 3. 连续型随机变量及其分布- 连续型随机变量的定义- 均匀分布、正态分布等常见分布 - 连续型随机变量的期望和方差三、概率密度函数与分布函数1. 概率密度函数- 概率密度函数的定义- 连续型随机变量的概率计算2. 分布函数- 分布函数的定义- 连续型和离散型随机变量的分布函数性质 - 分布函数的计算方法四、多维随机变量1. 二维随机变量- 二维随机变量的定义- 二维随机变量的概率密度函数和分布函数 2. 边缘分布与条件分布- 边缘分布的定义与计算- 条件分布的定义与计算3. 相关性与独立性- 相关性与协方差的关系- 独立性的定义与判定五、大数定律与中心极限定理1. 大数定律- 弱大数定律与强大数定律- 大数定律的应用2. 中心极限定理- 中心极限定理的定义- 中心极限定理的应用六、抽样与统计推断1. 抽样方法- 简单随机抽样- 分层抽样- 系统抽样2. 参数估计- 点估计与区间估计的概念 - 极大似然估计- 置信区间估计3. 假设检验- 假设检验的原理- 单侧与双侧假设检验- 显著性水平与p值总结：概率论作为统计学的基础学科，对于高校统计学专业的学生来说是非常重要的。

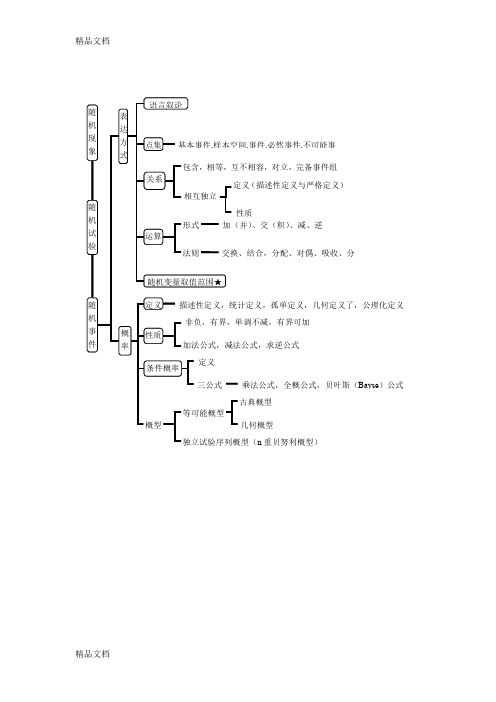
概率知识点总结框图一、概率基本概念1.1 概率的来源与发展概率论最早起源于赌博，18世纪以来，概率论在数学、统计学和随机过程等领域得到了广泛的应用，并逐渐形成了一门独立的学科。

现代概率论主要包括古典概率论、频率概率论和主观概率论等。

1.2 随机试验与样本空间随机试验是指以某种方式进行的实验，其结果是不确定的。

样本空间是随机试验所有可能结果的集合，用S表示。

1.3 事件与概率事件是样本空间的子集，表示试验的某种结果。

概率是事件发生的可能性大小的度量，通常用P(A)表示事件A的概率。

1.4 概率的性质概率的性质包括非负性、规范性和可列可加性等。

非负性：对于任意事件A，有P(A)≥0；规范性：样本空间S的概率为1，即P(S)=1；可列可加性：对于任意互斥事件序列{A1，A2，…}，有P(∪Ai)=ΣP(Ai)。

二、古典概率2.1 古典概率的定义古典概率是指在等可能的条件下，事件发生的概率等于有利结果数与总结果数的比值。

2.2 排列与组合排列是指从n个不同元素中取出m个元素，按一定顺序排成一列，其排列数为A(n,m)。

组合是指从n个不同元素中取出m个元素，不考虑顺序，其组合数为C(n,m)。

2.3 古典概率的计算古典概率的计算通常使用排列或组合的方法，根据古典概率的定义求解事件的概率。

三、条件概率3.1 条件概率的定义条件概率是指在事件B已发生的条件下，事件A发生的概率，表示为P(A|B)。

条件概率的计算公式为P(A|B)=P(AB)/P(B)。

3.2 乘法公式乘法公式是求事件A与事件B同时发生的概率的公式，表示为P(AB)=P(A|B)P(B)或P(AB)=P(B|A)P(A)。

3.3 全概率公式与贝叶斯公式全概率公式是指当事件A1，A2，…，An构成一个完全事件组，且事件B与每个Ai都有交集时，事件B的概率可以表示为P(B)=ΣP(B|Ai)P(Ai)。

贝叶斯公式是指当事件A1，A2，…，An构成一个完全事件组，且已知事件B的条件概率P(B|Ai)，可以求事件Ai的后验概率P(Ai|B)。

第一章:1.全概率公式：设S为某一实验的样本空间，A为该实验的事件，设B1，B2，B3，……，Bn是S的一个划分，且P（Bj）>0，j=1,2,3,……，n。

则P（A）=2.条件概率的全概率公式：P（A）=3.贝叶斯公式：~~~~~~~~~4.事件的独立性与独立试验（相互独立，两两独立，独立试验，重复试验）第二章：1.离散型随机变量（概率分布律，各种分布，概率分布函数）0-1分布二项分布泊松分布超几何分布2.连续型随机变量均匀分布正态分布指数分布其他（г分布，威布尔分布，β分布等）2.概率分布函数概率密度函数第三章：离散量连续量联合分布函数边际分布函数条件分布随机变量的独立性二元随机变量函数的分布（Z=X+Y的分布；M=Max（X,Y），N=Min（X,Y）的分布）第四章：1.数学期望公式：全（数学）期望公式2.方差公式：方差的性质：1.2.3.协方差与相关系数：对任意的正整数n，设X1，X2，…，Xn为方差存在的随机变量，则X1+X2+…+Xn的方差也存在，且若随机变量的协方差存在，则（协方差的性质）：1．2.3.4.5．6.相关系数：对于一些特定的分布，不相关与独立是等价的。

3．协方差矩阵多元正太随机分布第五章1.大数定律依概率收敛两个重要不等式几种大数定律2.中心极限定理独立同分布情形独立不同分布情形第六章1.总体和样本统计量样本均值样本方差样本标准差样本k阶（原点）矩样本k阶中心矩2．三个分布及其性质3.正太总体下的抽样分布第七章参数估计1.点估计矩法基本步骤1）2）3）极大似然法贝叶斯法2.估计量的评价准则无偏性准则有效性准则均方误差准则相合性准则3.区间估计置信区间轴枢量法4正太总体参数的区间估计单个正太总体的情形均值U的置信区间σ2已知σ2未知成对数据情形方差σ2的区间估计两个正太总体情形均值u1-u2的区间估计两总体的方差已知两总体的方差相同但未知两总体的方差不同且未知5.非正太总体参数的区间估计0-1分布其他分布均值u的区间估计第八章假设检验1.假设的提出统计量拒绝域两类错误显著水平P值与统计显著性处理假设检验问题的基本步骤2.单个正太总体参数的假设检验关于参数u的假设检验（方差已知和未知两种情况）成对数据的t检验有关参数σ2的假设检验3．两个正太总体参数的假设检验比较两样本均值以及方差的假设检验4.假设检验与区间估计5三种拟合优度检验第九章方差分析和回归分析1.单因素方差分析因素A引起的误差随机误差所引起的差异方差分析表均值的多重比较方差分析的前提2.双因素方差分析没有交互作用的双因素方差分析（无重复因素）有交互作用的双因素方差分析（有重复因素）3.相关系数4．一元线性回归数学模型参数估计以及参数的性质回归方程的显著性检验回归系数的区间估计。