自动控制原理图
- 格式:docx
- 大小:388.07 KB
- 文档页数:25






空调自动控制原理图
以下是空调自动控制的原理图,没有标题的文字。
1. 室内温度传感器:将室内温度转化为电信号。
2. 室外温度传感器:测量室外温度情况。
3. 室内湿度传感器:将室内湿度转化为电信号。
4. 室外湿度传感器:测量室外湿度情况。
5. 温度控制器:接收室内温度传感器的信号并与设定温度进行比较,根据比较结果控制空调开关或调整温度。
6. 湿度控制器:接收室内湿度传感器的信号并与设定湿度进行比较,根据比较结果控制空调开关或调整湿度。
7. 控制面板:提供操作界面,用户可以通过控制面板设置温度和湿度等参数。
8. 冷凝器:通过制冷剂的循环和传热,将室内热量排出去,降低室内温度。
9. 蒸发器:通过制冷剂的循环和传热,从室内吸收热量,提高室内温度。
10. 电风扇:控制室内空气的流动,使冷热空气均匀分布。
11. 压缩机:提供制冷剂的压缩和循环,实现室内空气的冷却。
12. 膨胀阀:控制制冷剂的流量,调节制冷效果。
以上是空调自动控制的原理图。
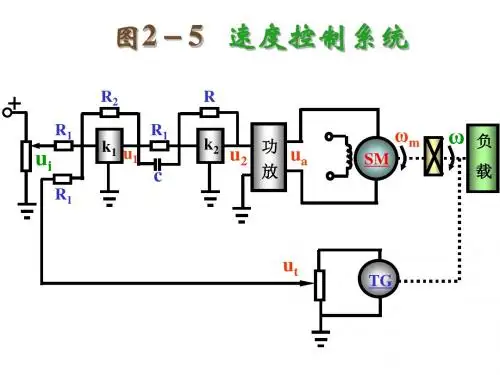


自动控制原理方框图自动控制原理方框图是指利用方框图的形式来描述自动控制系统的结构和工作原理。
方框图是自动控制原理中的重要工具,它能够直观地展示控制系统的各个部分之间的关系和作用,有助于工程师们更好地理解和设计控制系统。
在自动控制原理方框图中,通常包括输入端、输出端、控制器、执行器和被控对象等几个基本部分。
输入端是控制系统接收外部信号的地方,输出端则是控制系统输出控制信号的地方,控制器是控制系统的核心部分,它根据输入信号和系统反馈信息来生成控制信号,执行器则是根据控制信号执行相应的动作,被控对象则是控制系统需要控制的对象。
在方框图中,这几个部分通过箭头和线段连接起来,箭头表示信号的传递方向,线段则表示信号的传递路径。
通过这种方式,工程师们可以清晰地看到控制系统中各个部分之间的联系和作用,有助于他们更好地进行系统设计和调试。
在实际工程中,自动控制原理方框图被广泛应用于各种自动控制系统的设计和分析中。
无论是传统的PID控制系统,还是现代的模糊控制系统和神经网络控制系统,方框图都能够为工程师们提供直观的工具,帮助他们更好地理解和分析系统的结构和性能。
除此之外,自动控制原理方框图还能够为工程师们提供一个统一的语言和标准,方便他们之间的沟通和交流。
在实际工程中,不同的工程师可能来自不同的专业背景,有着不同的知识和经验,通过方框图,他们可以用统一的语言和标准来描述和分析控制系统,避免了因为专业术语和理论差异而导致的沟通障碍。
总的来说,自动控制原理方框图是自动控制原理中的重要工具,它能够直观地展示控制系统的结构和工作原理,有助于工程师们更好地理解和设计控制系统。
在实际工程中,方框图被广泛应用于各种自动控制系统的设计和分析中,为工程师们提供了一个统一的语言和标准,方便他们之间的沟通和交流。
因此,掌握自动控制原理方框图的基本原理和应用方法对于每一位自动控制工程师来说都是非常重要的。

Wn=0.4;
t=0:0.1:80;
num=[Wn^2];
zeta1=0;dem1=[1 2*zeta1*Wn Wn^2];
zeta2=0.5;dem2=[1 2*zeta2*Wn Wn^2];
zeta3=1.0;dem3=[1 2*zeta3*Wn Wn^2];
zeta4=1.5;dem4=[1 2*zeta4*Wn Wn^2];
zeta5=2.0;dem5=[1 2*zeta5*Wn Wn^2];
[y1,x,t]=impulse(num,[dem1,0],t);
[y2,x,t]=impulse(num,[dem2,0],t);
[y3,x,t]=impulse(num,[dem3,0],t); [y4,x,t]=impulse(num,[dem4,0],t);
[y5,x,t]=impulse(num,[dem5,0],t);
plot(t,y1,t,y2,t,y3,t,y4,t,y5)
grid on;
t=0:0.1:80;
num=[Wn^2];
zeta1=0;dem1=[1 2*zeta1*Wn Wn^2];
zeta2=0.5;dem2=[1 2*zeta2*Wn Wn^2];
zeta3=1.0;dem3=[1 2*zeta3*Wn Wn^2];
zeta4=1.5;dem4=[1 2*zeta4*Wn Wn^2];
zeta5=2.0;dem5=[1 2*zeta5*Wn Wn^2];
[y1,x,t]=step(num,dem1,t);
[y2,x,t]=step(num,dem2,t);
[y3,x,t]=step(num,dem3,t); [y4,x,t]=step(num,dem4,t);
[y5,x,t]=step(num,dem5,t);
plot(t,y1,t,y2,t,y3,t,y4,t,y5)
grid on;
Wn=0.4;
t=0:0.1:80;
num=[Wn^2];
zeta1=0;dem1=[1 2*zeta1*Wn Wn^2];
zeta2=0.5;dem2=[1 2*zeta2*Wn Wn^2];
zeta3=1.0;dem3=[1 2*zeta3*Wn Wn^2];
zeta4=1.5;dem4=[1 2*zeta4*Wn Wn^2];
zeta5=2.0;dem5=[1 2*zeta5*Wn Wn^2];
[y1,x,t]=step(num,[dem1,0],t);
[y2,x,t]=step(num,[dem2,0],t);
[y3,x,t]=step(num,[dem3,0],t); [y4,x,t]=step(num,[dem4,0],t);
[y5,x,t]=step(num,[dem5,0],t);
plot(t,y1,t,y2,t,y3,t,y4,t,y5)
grid on;
num=[1];
den=[1 10];
pzmap(num,den)
sgrid
num=[1];
den=[1 8 12 ]; pzmap(num,den) sgrid
num=[1 2];
den=[1 7 15 9]; rlocus(num,den) sgrid
num=[1 3];
den=[1 12 70 100 0]; rlocus(num,den)
sgrid
num=[1 5.5 11 7.5]; den=[1 3.5 5 6.25 0]; rlocus(num,den)
sgrid
num=[1 5.5 11 7.5];
den=[1 3.5 5 6.25 0]; [k,p]=rlocfind(num,den) rlocus(num,den)
sgrid
num=1;
den=1;
bode(num,den); grid
num=1;
den=[1,0]; bode(num,den); grid
num=[1,0];
den=1;
bode(num,den); grid
num=1;
den=[1,1]; bode(num,den); grid
num=[1,1];
den=1;
bode(num,den); grid
num=1;
wn=10;
zeta=[0.1:0.1:1.2];
hold on
for z=zeta
den=[(1/wn)^2 2*z/wn 1];
sys=tf(num,den);
bode(sys)
end
title
hold off
num=[1];
zeta1=[0.1];den1=[0.01 0.2*zeta1 1]; zeta2=[0.3];den2=[0.01 0.2*zeta2 1]; zeta3=[0.5];den3=[0.01 0.2*zeta3 1]; zeta4=[0.7];den4=[0.01 0.2*zeta4 1]; zeta5=[0.8];den5=[0.01 0.2*zeta5 1]; zeta6=[0.9];den6=[0.01 0.2*zeta6 1]; zeta7=[1.0];den7=[0.01 0.2*zeta7 1]; zeta8=[1.1];den8=[0.01 0.2*zeta8 1]; zeta9=[1.2];den9=[0.01 0.2*zeta9 1]; [re1,im1]=nyquist(num,den1);
[re2,im2]=nyquist(num,den2);
[re3,im3]=nyquist(num,den3);
[re4,im4]=nyquist(num,den4);
[re5,im5]=nyquist(num,den5);
[re6,im6]=nyquist(num,den6);
[re7,im7]=nyquist(num,den7);
[re8,im8]=nyquist(num,den8);
[re9,im9]=nyquist(num,den9);
plot(re1,im1,re2,im2,re3,im3,re4,im4,re5,im5,re6,im6,re7,im7,re8,im8,re 9,im9);
grid
title('振荡环节奈氏图')
num=[1,1];
den=[1,0];
bode(num,den);
grid
num=[1,1,1]; den=[1,0]; bode(num,den); grid
sys=tf([250 200],[1 4.2 100.8 20 0]); subplot(2,1,1)
nyquist(sys)
subplot(2,1,2)
bode(sys)
h1=tf([250 200],[1 0.2 0]);
h2=tf([1],[1 4 100]);
h=h1*h2;
[num,den]=tfdata(h);
[mag,phase,w]=bode(num,den);
subplot(211);
semilogx(w,20*log10(mag));grid; subplot(212);
semilogx(w,phase);grid;
[gm,pm,wcg,wcp]=margin(mag,phase,w)
G1=tf(35,conv([0.002 0.21 1 0],[0.005,1]));
[mag phase w]=bode(G1);
magdb=20*log10(mag);
subplot(211);
bode(G1);
margin(mag,phase,w);
G2=tf(35*[0.2 3 10],conv([0.002 0.21 1 0],[0.005,1,0])); [mag phase w]=bode(G2);
magdb=20*log10(mag);
subplot(212);
bode(G2,'--');
margin(mag,phase,w);
G1=tf(35,conv([0.002 0.21 1 0],[0.005,1])); G2=tf([0.2,3,10],[1 0]);
figure;
G1_c=feedback(G1,1);
G2_c=feedback(G2,1);
step(G1_c);
hold;
step(G2_c,'--');
G1=tf(35,[0.000001,0.00305,0.11,1,0]);
G2=tf(35*[0.2,3,10],conv([0.000001,0.00305,0.11,1,0],[1,0])) bode(G1)
hold
bode(G2,'--')
figure
G1_c=feedback(G1,1)
G2_c=feedback(G2,1)
step(G1_c)
hold
step(G2_c,'--')
G1=tf(100,[0.04,1,0]);
G2=tf(100*[0.025,1],conv([0.04,1,0],[0.01,1])) bode(G1)
hold
bode(G2,'--')
figure
G1_c=feedback(G1,1)
G2_c=feedback(G2,1)
step(G1_c)
hold
step(G2_c,'--')。