第三单元分数除法整理复习

人教版数学六年级上册第3单元《分数除法整理和复习（第
2课时）》教案
一、教学目标
1.知识与能力：学生能够理解分数除法的概念，能够进行简单的分数除
法计算。

2.过程与方法：能够运用适当的方法解决分数除法问题。

3.情感态度与价值观：培养学生正确的学习态度，激发学生对数学学习
的兴趣。

二、教学重点
1.掌握分数除法的概念。

2.能够运用适当的方法进行分数除法计算。

三、教学难点
1.分数除法的应用。

2.复杂分数除法的解决方法。

四、教学过程
1. 导入新知
老师可以通过提问引入新知识，例如：“什么是分数除法？可以举例说明吗？”
2. 学习新知
1.呈现分数除法的定义和基本概念。

2.通过例题帮助学生理解分数除法的运算方法。

3. 练习
让学生做一些简单的练习题，巩固分数除法的概念和方法。

4. 拓展
引导学生探讨分数除法在实际生活中的应用，如何将分数除法运用到解决问题中。

5. 总结
让学生总结本节课学到的知识点和解题方法，强化学习效果。

五、课堂作业
完成课堂练习题，并写出解题步骤。

六、板书设计
•分数除法的定义
•分数除法的运算方法
•分数除法的应用
七、教学反思
本节课教学内容较为简单，学生表现积极，但在分数除法的应用方面仍需加强，下节课将重点讲解分数除法的实际运用。

以上为本节课教案，希望能够帮助学生更好地理解和掌握分数除法的相关知识。

第三单元 分数除法（一）倒数1、意义：乘积为1的两个数互为倒数。

◆倒数是两个数的关系，它们互相依存，不能单独存在。

单独一个数不能称为倒数。

（必须说清谁是谁的倒数）2、判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为“1”。

例如：a ×b ＝1则a 、b 互为倒数。

3、求倒数的方法： ①求分数的倒数：交换分子、分母的位置。

（a b 的倒数是ba ） ②求整数的倒数：整数分之一。

（非零整数a(a ≠0)，它的倒数为a 1） ③求带分数的倒数：先化成假分数，再交换分子和分母的位置。

④求小数的倒数：先化成分数再求倒数。

4、特殊数的倒数：①1的倒数是它本身，因为1×1=1②0没有倒数，因为任何数乘0积都是0，且0不能作分母。

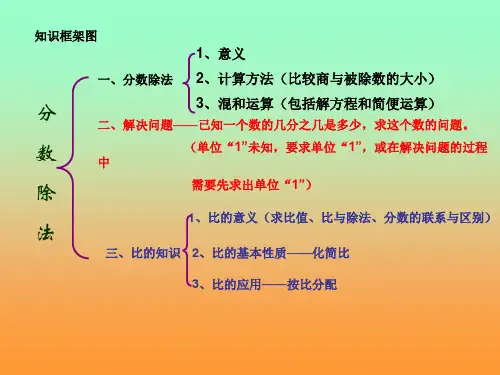
（二）分数除法1、意义：（分数除法是分数乘法的逆运算），已知两个数的积与其中一个因数，求另一个因数的运算。

或是求一个数中包含了几个另一个数。

2、计算法则：除以一个数（0除外），等于乘上这个数的倒数。

被除数÷除数=被除数×除数的倒数。

例 53÷3＝53×31＝51 3÷53＝3×35＝5 ◆除法转化成乘法时，被除数一定不能变，“÷”变成“×”，除数变成它的倒数。

3、分数除法算式中出现小数、带分数时要先化成分数、假分数再计算。

4、被除数与商的变化规律：①除以大于1的数，商小于被除数：a÷b=c 当b>1时，c<a (a ≠0)②除以小于1的数，商大于被除数：a÷b=c 当b<1时，c>a (a ≠0 b ≠0) ③除以等于1的数，商等于被除数：a÷b=c 当b=1时，c=a（三）分数混合运算：同整数。

（四）分数除法应用题1、分数乘除法应用题的对比①已知单位“1”的量用乘法。

例：甲是乙的53，乙是25，求甲是多少？即：甲＝乙×53 —→ 25×53=15 ②未知单位“1”的量用除法（或方程）。

六年级数学知识点：第三单元分数除法一、分数除法的意义：分数除法是分数乘法的逆运算，已知两个数的积与其中一个因数，求另一个因数的运算。

二、分数除法计算法则：除以一个数(0除外)，等于乘上这个数的倒数。

1、被除数divide;除数=被除数times;除数的倒数。

例 divide;3= times; = 3divide; =3times; =52、除法转化成乘法时，被除数一定不能变，“divide;”变成“times;”，除数变成它的倒数。

3、分数除法算式中出现小数、带分数时要先化成分数、假分数再计算。

4、被除数与商的变化规律：①除以大于1的数，商小于被除数：adivide;b=c 当bgt;1时，c②除以小于1的数，商大于被除数：adivide;b=c 当blt;1时，cgt;a (ane;0 bne;0)③除以等于1的数，商等于被除数：adivide;b=c 当b=1时，c=a三、分数除法混合运算1、混合运算用梯等式计算，等号写在第一个数字的左下角。

2、运算顺序：①连除：属同级运算，按照从左往右的顺序进行计算;或者先把所有除法转化成乘法再计算;或者依据“除以几个数，等于乘上这几个数的积”的简便方法计算。

加、减法为一级运算，乘、除法为二级运算。

②混合运算：没有括号的先乘、除后加、减，有括号的先算括号里面，再算括号外面。

注：(ab)divide;c=adivide;cbdivide;c四、比：两个数相除也叫两个数的比1、比式中，比号(∶)前面的数叫前项，比号后面的项叫做后项，比号相当于除号，比的前项除以后项的商叫做比值。

注：连比如：3：4：5读作：3比4比52、比表示的是两个数的关系，可以用分数表示，写成分数的形式，读作几比几。

例：12∶20= =12divide;20= =0.6 12∶20读作：12比20注：区分比和比值：比值是一个数，通常用分数表示，也可以是整数、小数。

比是一个式子，表示两个数的关系，可以写成比，也可以写成分数的形式。

六年级数学上册第三单元分数除法知识点总结1、倒数的意义: 乘积是1的两个数互为倒数。

强调:互为倒数，即倒数是两个数的关系，它们互相依存，倒数不能单独存在。

(要说清谁是谁的倒数)。

2、求倒数的方法:（1）、求分数的倒数：交换分子分母的位置。

（2）、求整数的倒数：把整数看做分母是1的分数，再交换分子分母的位置。

（3）、求带分数的倒数：把带分数化为假分数，再求倒数。

（4）、求小数的倒数：把小数化为分数，再求倒数。

3、1的倒数是1; 因为1×1=1;0没有倒数，因为0乘任何数都得0，(分母不能为0) 。

4、真分数的倒数大于1;假分数的倒数小于或等于1;带分数的倒数小于1。

5、运用，a×2/3=b×1/4求a和b是多少。

把a×2/3=b×1/4看成等于1,也就是求2/3的倒数和求1/4的倒数。

6、分数除法的意义：分数除法与整数除法的意义相同，表示已知两个因数的积和其中一个因数，求另一个因数的运算。

乘法：因数×因数=积除法：积÷一个因数=另一个因数7、分数除法的计算法则：除以一个不为0的数，等于乘这个数的倒数。

8、分数除法比较大小时的规律：(1)当除数大于1，商小于被除数;(2)当除数小于1(不等于0)，商大于被除数;(3)当除数等于1，商等于被除数。

9、分数除法解决问题（不知单位“1”的量（用除法）找单位“1”：在分率句中分率的前面；或“占”、“是”、“比”的后面。

10、解法：(1)方程：根据数量关系式设未知量为X，用方程解答。

解：设未知量为X (一定要解设),再列方程用 X×分率=具体量(2)算术(用除法)：单位“1”的量未知用除法：即已知单位“1”的几分之几是多少，求单位“1”的量。

分率对应量÷对应分率 = 单位“1”的量(3)看分率前有没有比多或比少的问题;分率前是“多或少”的关系式：(比少)：具体量÷ (1-分率)= 单位“1”的量;(比多)：具体量÷ (1+分率)= 单位“1”的量(4)求一个数是另一个数的几分之几是多少：用一个数除以另一个数，结果写为分数形式。

最新版六年级数学上册第三单元分数除法1.分数除法计算（1）分数除法的意义和分数除以整数整数除法的意义：已知两个因数的积与其中一个因数，求另一个因数的运算。

已知两个因数的积与其中一个因数，求另一个因数，用（除法）计算。

1013103=÷的意义是：已知两个因数的积是103，其中一个因数是3，求另一个因数是多少。

分数除法的意义与整数除法的意义相同，都是已知两个因数的积与其中一个因数，求另一个因数的运算。

分数除以整数的计算方法把一个数平均分成整数份，求其中的几份就是求这个数的几分之几是多少。

分数除以整数（0除外）的计算方法：（1）用分子和整数相除的商做分子，分母不变。

（2）分数除以整数，等于分数乘这个整数的倒数。

练习： 1.填空（1）根据3565372=⨯和分数除法意义可得：=÷53356（ ），=÷72356（ ）。

（2）把29m 长的绳子平均剪成4段，每段是29m 的（ ）。

（3）打字员打一份文件，打了20分钟后还剩52，平均每分钟打这份文件的（ ）。

2.列式计算。

（1）一个数的6倍是51，这个数是多少？（2）51的61是多少？3.看图列式计算。

811（2）一个数除以分数知识点一：一个数除以分数的计算方法：一个数除以分数，等于这个数乘分数的倒数。

知识点二：分数除法的统一计算法则：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

知识点三：商与被除数的大小关系：一个数（0除外）除以小于1的数，商大于被除数，除以1，商等于被除数，除以大于1的数，商小于被除数。

0除以任何数商都为0.练习：1.算一算4851625÷ 44392213÷ 1427277⨯ 210÷2.填空。

（1）32的43是（ ），它和32÷（ ）得数相同。

（2）分数除法可以转化为（ ）进行计算，计算过程中，转变成乘（ ）的倒数。

4.判断。

（1）两个真分数相除，商大于被除数。

第三单元《分数除法》整理和复习教学时间：年月日教学课时：2 课时课型：复习课教学内容：第一课时复习分数除法的意义和计算（教材第46、47页的内容），第二课时复习分数除法应用题（教材第46、47页的内容）教学目标：1.使学生进一步明确本单元的知识体系，加深对分数除法的意义和计算方法的理解。

通过复习比较，进一步弄清分数乘、除法应用题在数量关系和解题思路等方面的联系和区别。

2. 熟练掌握分数除法的计算法则，提高灵活解题的能力。

进一步掌握用方程或算术方法解答“已知一个数的几分之几是多少，求这个数”的应用题，提高学生解答分数应用题的能力。

3. 在整理知识体系的过程中，帮助学生掌握复习的方法。

培养学生独立思考、认真审题的好习惯。

教学重点：概念和计算法则的整理。

建立三类分数应用题之间的联系，能够比较准确地分析、解决较复杂的实际问题。

教学难点：运用所学概念，灵活解决问题。

建立三类分数应用题之间的联系，能够比较准确地分析、解决较复杂的实际问题。

教学准备：课件教材分析：1.结合操作活动和图形语言，探索并理解分数除法的意义及计算方法，采用对比的方法，揭示分数除法的意义在分数除法的教学中，教材采用了整数与分数对比，乘法与除法对比的方式，揭示出分数除法的意义与整数除法的意义相同，都是已知两个因数的积与其中一个因数，求另一个因数的运算。

探索分数除以整数的计算方法，明白算理在分数除以整数这个环节中，教材设计了“折一折、涂一涂”等活动，让学生在实际操作中借助图形语言，利用已学过的分数乘法的意义，解决有关分数除法的问题，在充分体验的基础上总结出分数除以整数的计算方法。

2、结合操作活动和图形语言，进一步探索并理解分数除法的意义及计算方法：根据已有的数量关系，引出一个数除以分数的计算在分数除以整数的基础上，研究一个数除以分数的计算，这是一个难点。

3、在解决实际问题的过程中，理解分数混合运算的计算方法（1）通过解决问题，理解分数混和运算的顺序，通过解决问题，引出涉及分数除法的混合运算，使学生看到已经掌握的混合运算顺序，同样适用于分数运算。

人教版六年级数学上册第三单元【学习目标】1、进一步掌握本章所学的基本概念和计算法则。

2、掌握用方程或算术方法解答已知一个数的几分之几是多少求这个数的应用题和稍复杂的分数乘除法应用题,提高计算能力和解答分数应用题的能力。

3、养成认真完成作业的好习惯，感受学习数学的乐趣。

【学习重难点】1、重点：分数除法的计算方法，化简比以及正确解答分数应用题。

2、难点：正确计算分数除法，提高解答分数应用题的能力。

×=（）43B AA ÷=B A ÷B=4343B A 除法是乘法的逆运算分数除法甲数除以乙数（0除外）等于甲数（）乙数的（）乘98÷4=815145÷3=÷=45 倒数分数混合运算的运算顺序：先乘除、后加减，有括号先算括号里的。

说出下面各题的运算顺序2－÷－61392623×[ －( －)]493414716÷（1－－）141214÷3＋×323545133－×－102127= ×＋×35134513=( ＋)×354513=1×13=13=3－－5727=3－（＋）5727=3－1=2－) ×40585.4×＋3.6÷910109黑兔只数相当于白兔的83甲数占乙数的43女生人数的是男生人数73实际比计划增产41王爷爷家养鸡30只，养鸡的只数是鸭的。

王爷爷家养鸭多少只？65王爷爷家养鸡30只，养鸭的只数是鸡的。

王爷爷家养鸭多少只？65一个牧场30头牛，牛的数量比羊少养羊多少只？94一个牧场，养了30头牛，羊的数量比牛少养羊多少只？94小华体重30千克，小丽比小华重,小丽体重多少千克？61小华体重30千克，比小刚重,小刚体重多少千克？61一辆汽车从甲地开往乙地，行了全程的，正好行了81千米。

两地间的公路长多少千米？一辆汽车从甲地开往乙地，行了全程的，离乙地还有135千米。