福建省三明市六县2020-2021学年七年级上学期期末考试数学试题

2020-2021学年福建省三明市七年级上期末数学试卷一．选择题（共10小题，满分40分，每小题4分）
1．下列四个图形中，不能作为正方体的展开图的是（）
A．B．
C．D．
2．如图，有理数a，b，c在数轴上的位置，则下列选项正确的是（）
A．a＜b＜0＜c B．a＜c＜0＜b C．b＜0＜a＜c D．c＜a＜0＜b 3．|a|＝1，|b|＝4，且ab＜0，则a+b的值为（）
A．3B．﹣3C．±3D．±5
4．计算﹣4×（﹣2）的结果等于（）
A．12B．﹣12C．8D．﹣8
5．下列计算不正确的是（）
A．（−1
2）
3=−1
8
B．（﹣6）2＝36
C．（﹣1）2n+1＝1（n是正整数）
D．（﹣1）2n＝1（n是正整数）
6．如果关于a，b的代数式a2m﹣1b与a5b m+n是同类项，那么（mn+5）2019等于（）A．0B．1C．﹣1D．52019
7．为调查某中学学生对社会主义核心价值观的了解程度，某课外活动小组进行了抽样调查，以下样本最具有代表性的是（）
A．初三年级的学生对社会主义核心价值观的了解程度
B．全校女生对社会主义核心价值观的了解程度
C．每班学号尾号为5的学生对社会主义核心价值观的了解程度
第1 页共17 页。

福建省三明市2021年七年级上学期数学期末考试试卷D卷姓名:________ 班级:________ 成绩:________一、单选题 (共7题；共14分)1. （2分）我国最长的河流长江全长约为6300千米，用科学记数法表示为（）A . 63×102千米B . 6.3×103千米C . 6.3×104千米D . 6.3×106千米2. （2分）如图，一个几何体由5个大小相同、棱长为1的正方体搭成，下列关于这个几何体的说法错误的是（）A . 主视图的面积为4B . 左视图的面积为3C . 俯视图的面积为4D . 搭成的几何体的表面积是203. （2分） (2016七上·蓟县期中) 如图所示，a、b、c表示有理数，则a、b、c的大小顺序是（）A . a＜b＜cB . a＜c＜bC . b＜a＜cD . c＜b＜a4. （2分） (2020七下·高新期中) 下列命题中，真命题有（）①垂线段最短；②全等三角形的周长相等；③在同一平面内，平行于同一直线的两条直线平行；④对顶角相等。

A . 1个B . 2个C . 3个D . 4个5. （2分） (2019七下·仁寿期中) 用不等式表示“a的一半不小于-7”，正确的是（）A . a≥-7B . a≤-7C . a>-7D . a<-76. （2分）如图，已知直线EF⊥MN垂足为F，且∠1=140°，则当∠2等于（）时，AB∥CD．A . 50°B . 40°C . 30°D . 60°7. （2分）如图是一张矩形纸片ABCD，AD＝10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE＝6cm，则CD＝（）A . 4cmB . 6cmC . 8cmD . 10cm二、填空题 (共12题；共15分)8. （1分）(2016·云南) |﹣3|=________．9. （1分） (2018七上·北京月考) 的系数是________，次数是________．10. （1分） (2017七上·启东期中) 关于x的方程7x﹣5=kx+9有正整数解，则整数k的值为________．11. （1分） (2017七上·洪湖期中) 请你取一个x的值，使代数式的值为正整数，你所取的x的值是________．12. （1分）合并同类项：－2a2＋4a2＝________，3x－2y－7x＋3y＝________．13. （1分） (2016八上·杭州期末) 已知关于x的一元一次方程4x+m﹣1=3m+1的解是负数，则m的取值范围是________．14. （2分） (2019·呼和浩特模拟) 如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE ，且点F在矩形ABCD内部．将AF延长交边BC于点G ．若＝，则＝________用含k 的代数式表示）．15. （2分） (2019七上·淮安月考) 若，则 =________.16. （2分）(2018·凉州) 已知某几何体的三视图如图所示，其中俯视图为正六边形，则该几何体的表面积为________．17. （1分） (2017七上·召陵期末) 计算：15°37′+42°51′=________18. （1分） (2018七上·镇江月考) - 的相反数是________，- 的倒数是________，- 的绝对值是________．19. （1分） (2018七上·辽阳月考) 若关于x的一元一次方程 =1的解是x=-1，则k=________.三、解答题 (共8题；共55分)20. （10分） (2019七上·沙河口期末) 计算:（1）（2）21. （10分） (2019七上·淮安月考) 若规定一种运算，（1）计算：；（2），则x是多少？22. （5分） (2019七上·朝阳期末) 先化简，再求值：，其中．23. （5分）如图，已知数轴上A、B两点所表示的数分别为﹣2和8．（1）求线段AB的长；（2）若P为射线BA上的一点（点P不与A、B两点重合，M为PA的中点，N为PB的中点，当点P在射线BA 上运动时；MN的长度是否发生改变？若不变，请你画出图形，并求出线段MN的长；若改变，请说明理由．24. （6分） (2019七上·下陆期末) 如图，我们知道，从A地到B地有四条道路，除它们外，可以再修一条从A地到B地的最短道路.解答下列问题：（1）请你在图上画出最短线路？（2）你这样画的理由是“两点决定一条直线”呢，还是“两点之间，线段最短”？（3）如果已知三点A、B、C在同一条直线上，且AB＝5，BC＝2，求AC的长.25. （10分） (2018七上·从化期末) 如图，数轴上点A表示的数为8，B是数轴上一点，且AB＝14，动点P 从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t＞0)秒．（1）点B表示的数为________，点P表示的数为________（用含t的式子表示）；（2）动点H从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P,H同时出发，问点P运动多少秒时追上点H?26. （7分） (2016九上·扬州期末) 已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．（1）如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；（2）如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF．27. （2分） (2017七上·北京期中) 阅读下面材料并解决有关问题：我们知道：|x|= ．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1=0和x﹣2=0，分别求得x=﹣1，x=2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x=﹣1和，x=2可将全体实数分成不重复且不遗漏的如下3种情况：①x＜﹣1；②﹣1≤x＜2；③x≥2．从而化简代数式|x+1|+|x﹣2|可分以下3种情况：①当x＜﹣1时，原式=﹣（x+1）﹣（x﹣2）=﹣2x+1；②当﹣1≤x＜2时，原式=x+1﹣（x﹣2）=3；③当x≥2时，原式=x+1+x﹣2=2x﹣1．综上讨论，原式= ．通过以上阅读，请你解决以下问题：（1）化简代数式|x+2|+|x﹣4|．（2）求|x﹣1|﹣4|x+1|的最大值．参考答案一、单选题 (共7题；共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、二、填空题 (共12题；共15分)8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、三、解答题 (共8题；共55分) 20-1、20-2、21-1、21-2、22-1、23-1、24-1、24-2、24-3、25-1、25-2、26-1、26-2、27-1、27-2、。

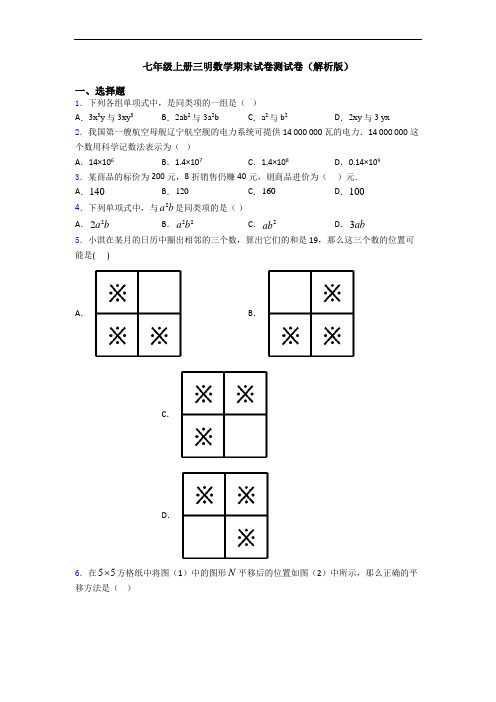
七年级上册三明数学期末试卷测试卷（解析版）一、选择题1．下列各组单项式中，是同类项的一组是（）A．3x3y与3xy3B．2ab2与-3a2b C．a2与b2D．2xy与3 yx2．我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的电力．14 000 000这个数用科学记数法表示为（）A．14×106B．1.4×107C．1.4×108D．0.14×1093．某商品的标价为200元，8折销售仍赚40元，则商品进价为（）元．A．140B．120C．160D．1004．下列单项式中，与2a b是同类项的是（）ab D．3abA．2a b C．22a b B．225．小淇在某月的日历中圈出相邻的三个数，算出它们的和是19，那么这三个数的位置可能是( )A．B．C．D．方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平6．在55移方法是（）（1）（2）A ．先向下移动1格，再向左移动1格；B ．先向下移动1格，再向左移动2格C ．先向下移动2格，再向左移动1格：D ．先向下移动2格，再向左移动2格7．小明在某月的日历中圈出了三个数，算出它们的和是14，那么这三个数的位置可能是（ ） A ．B ．C ．D ．8．化简：35xy xy -的结果是（ ） A ．2B ．2-C ．2xyD ．2xy -9．将一副直角三角尺按如图所示摆放，图中锐角∠1的度数为（ ）A ．58°B ．59°C ．60°D ．61° 10．若a ＞b ，则下列不等式中成立的是（ ）A ．a +2＜b +2B ．a ﹣2＜b ﹣2C ．2a ＜2bD ．﹣2a ＜﹣2b11．在一列数:123n a a a a ⋯，，，中，12=7=1a a ，， 从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这个数中的第2018个数是（） A ．1 B ．3 C ．7 D ．9 12．对于代数式3m +的值，下列说法正确的是（ ）A ．比3大B ．比3小C ．比m 大D ．比m 小13．我区深入实施环境污染整治，关停和整改了一些化工企业，使得每年排放的污水减少了167000吨．将167000用科学记数法表示为（ ） A ．316710⨯ B ．416.710⨯ C ．51.6710⨯ D ．60.16710⨯ 14．地球上陆地的面积约为1490000002km ，数149000000科学记数法可表示为( ) A ．90.14910⨯， B ．81.4910⨯ C ．714.910⨯ D ．614910⨯ 15．对于任何有理数a ，下列各式中一定为负数的是（ ）A ．(3)a --+B ．2a -C ．1a -+D ．1a --二、填空题16．3615︒'的补角等于___________︒___________′.17．若关于x 的方程5x ﹣1＝2x +a 的解与方程4x +3＝7的解互为相反数，则a ＝________．18．要在墙壁上固定一根小木条，至少需要两枚钉子，其数学原理是_____．19．12-的相反数是_________.20．按照下图程序计算：若输入的数是-3 ，则输出的数是________21．若∠1+∠2=90°，∠2+∠3=90°，则∠1=∠3．理由是______．22．线段AB=10cm，BC=5cm，A、B、C三点在同一条直线上，则AC=______．23．实验室里，水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高)，底面半径之比为1:2:1，用两根相同的管子在容器的5cm高度处连接(即管子底端离容器底5cm)，现三个容器中，只有甲中有水，水位高1cm，如图所示.若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位高度为56cm，则开始注入________分钟的水量后，甲与乙的水位高度之差是16 cm.24．已知∠α＝28°，则∠α的余角等于___．25．若如图的平面展开图折叠成正方体后，“泽”相对面上的字为_________三、解答题26．如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．()1过点C画线段AB的平行线CD；()2过点A画线段BC的垂线，垂足为E；()3过点A画线段AB的垂线，交线段CB的延长线于点F；()4线段AE 的长度是点______到直线______的距离； ()5线段AE 、BF 、AF 的大小关系是______.(用“<”连接)27．计算：（1）715|4|--- （2）42112(3)6⎛⎫--⨯-÷-⎪⎝⎭28．如图，已知三角形ABC ，D 为AB 边上一点．(1) 过点D 画线段BC 的平行线DE ，交AC 于点E ；过点A 画线段BC 的垂线AH ，垂足为点H ．(2)用符号语言分别描述直线DE 与线段BC 及直线AH 与线段BC 的位置关系． (3)比较大小：线段BH 线段BA ，理由为 ．29．解方程 （1）528x +=- （2）4352x x -=+ （3）()4232x x -=-- （4）2151136x x +--= 30．一项工程由甲单独做需12天完成，由乙单独做需8天完成，若两人合作3天后，剩下部分由乙单独完成，乙还需做多少天？31．先化简，在求值：221523243m mn mn m ⎡⎤⎛⎫--++ ⎪⎢⎥⎝⎭⎣⎦，其中2m =-，12n = 32．数轴是初中数学的一个重要工具，利用数轴可以将数与形完美结合．研究数轴时，我们发现有许多重要的规律:例如，若数轴上点 A , B 表示的数分别为 a , b ，则 A , B 两点之间的距离AB=a-b ，线段 AB 的中点M 表示的数为2a b+．如图，在数轴上，点A,B,C 表示的数分别为-8，2，20．（1）如果点A和点C都向点B运动，且都用了4秒钟，那么这两点的运动速度分别是点A 每秒_______个单位长度、点C每秒______个单位长度；（2）如果点A以每秒1个单位长度沿数轴的正方向运动，点C以每秒3个单位长度沿数轴的负方向运动，设运动时间为t秒，请问当这两点与点B距离相等的时候，t为何值？（3）如果点A以每秒1个单位长度沿数轴的正方向运动，点B以每秒3个单位长度沿数轴的正方向运动，且当它们分别到达C点时就停止不动，设运动时间为t秒，线段AB的中点为点P；①t为何值时PC=12；②t为何值时PC=4．33．如图，数轴上A，B两点表示的数分别为a，b，且a，b满足|a+5|+（b﹣10）2＝0．（1）则a＝，b＝；（2）点P，Q分别从A，B两点同时向右运动，点P的运动速度为每秒5个单位长度，点Q的运动速度为每秒4个单位长度，运动时间为t（秒）．①当t＝2时，求P，Q两点之间的距离．②在P，Q的运动过程中，共有多长时间P，Q两点间的距离不超过3个单位长度？③当t≤15时，在点P，Q的运动过程中，等式AP+mPQ＝75（m为常数）始终成立，求m 的值．四、压轴题34．探索、研究：仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…)，受堆放条件限制，堆放时应符合下列条件：每层堆放仪器箱的个数a n与层数n之间满足关系式a n=n²−32n+247，1⩽n<16，n为整数。

2020－2021学年第一学期期末六县质量检测七年级数学试题参考答案一.选择题（本大题共10小题，每小题4分,每题只有一个正确答案,共40分）1．D ； 2．B ； 3．B ； 4．A ； 5．A ； 6．D ； 7.C ； 8.A ； 9. C ； 10.B二.填空题(本大题共6小题, 每小题4分，共24分)11．6-; 12．105; 13．0 ； 14．30； 15．()945324+-⨯=； 16．132-. 三. 解答题（本大题共9小题，共86分）17．（8分）解：（1）原式＝（－12）×（－43）+（－12）×65 …………………… 2分 ＝-9-10……………………… 3分＝-19……………………… 4分（2）原式＝8-（－12）×31×41 …………………… 6分 ＝8+1……………………… 7分＝9……………………… 8分18.（8分）解： （1）215109x x -+=…………………… 2分1224x =…………………… 3分2.x =…………………… 4分（2）()()312216x x +--=…………………… 6分33426x x +-+=…………………… 7分1.x =-…………………… 8分19. （8分）解： (55)5(25)6a a b ab --+-+＝55510256a a ab ab ---++…………………… 4分＝4+20ab -…………………… 6分当1,2021a b =-=时，原式＝()412021208104.-⨯-⨯+=…………………… 8分20．（8分）解：（每图4分）21．（8分）解：（1）因为OD 平分∠AOC ,∠AOC ＝54°，所以∠AOD ＝∠COD ＝12∠AOC ＝27°，…………… 2分所以∠DOB ＝180°-∠AOD ＝180°-27°＝153°；…………… 4分（2）理由：因为∠DOE ＝90°，所以∠EOC ＝90°-27°＝63°，…………… 5分因为∠BOC ＝180°-54°＝126°所以∠BOE ＝126°-63°＝63°，…………… 6分所以∠BOE ＝∠EOC ，…………… 7分所以OE 是否平分∠COB ……… 8分22. （10分）解：（1） 8 …………… 3分（2）7分（3）根据题意得：4360051650⨯=人， 答：该校学生数学成绩合格的人数大约516人……… 10分23．（10分）解：（1）13，125；------------4分 （2）0,425x x x >+<+因为所以42+525(4)1112222x x x x x ++-++÷==所以，从正面看 从左面看31=,821又因为13,2x x +==所以解得------------7分（3）53 1.x =或或------------10分24. （12分）解：（1）设A 型空调销售x 台，则B 型空调销售()52x -台------------1分 ()2000300052126000x x +-= ------------3分解得30x = ------------4分523022-=（台）------------5分答：A 型空调销售30台，B 型空调销售22台. ------------6分（2）所以销售额3万时，可得工资：()500030000200005500+-⨯％=5（元） 销售额4万时，可得工资：()()500030000200005400003000080+-⨯+-⨯％％=630（元）所以550059806300<<所以销售额超过3万元但不超过4万元------------7分设销售总额y 元，则()()5000300002000053000080y +-⨯+-⨯％％=598------------8分 36000y = ------------9分所以销售员甲本月销售总额为36000元------------10分25．（14分）（1）–6； ------------3分（2）因为长方形ABCD 的面积为10，所以A B =5.①当S=8时，若长方形ABCD 向左平移，重叠部分中的A ＇B =4，所以AA ＇=1.则点A ＇表示–1–1= – 2. ------------6分若长方形ABCD 向右平移，重叠部分中的AB ＇=4，所以AA ＇=1.则点A ＇表示–1+1= 0.所以点A ＇表示的数为– 2或0. ------------9分①根据题意可知，E 表示的数为1,t -+ F 表示的数为26.3t -+------------11分 21603t t ⎛⎫-++-+= ⎪⎝⎭所以21.5t =解得------------14分。

福建省三明市六县统考七年级（上）期末数学试卷一、选择题（共10小题，每小题2分，满分20分每小题只有一个正确的选项）1．﹣9的相反数是（）A．B．﹣C．9D．﹣92．计算（﹣2）×3的结果是（）A．﹣5B．﹣6C．1D．63．下列说法正确的是（）A．射线PA和射线AP是同一条射线B．射线OA的长度是12cmC．直线ab、cd相交于点MD．两点确定一条直线4．下列问题，适合抽样调查的是（）A．了解一批灯泡的使用寿命B．学校招聘老师，对应聘人员的面试C．了解全班学生每周体育锻炼时间D．上飞机前对旅客的安检5．下面四个立体图形，从正面、左面、上面对空都不可能看到长方形的是（）A．B．C．D．6．经专家估算，南海属我国传统疆线以内的油气资源约合15000亿美元，用科学记数法表示数字15000是（）A．15×103B．1.5×103C．1.5×104D．1.5×1057．下列运算正确的是（）A．x﹣3y=﹣2xy B．5x2﹣2x2=3x2C．x2+x3=x5D．2x2y﹣xy2=xy8．如图，数轴上有M，N，P，Q四个点，其中点P所表示的数为a，则数﹣3a所对应的点可能是（）A．M B．N C．P D．Q9．下列方程的变形中正确的是（）A．由x+5=6x﹣7得x﹣6x=7﹣5B．由﹣2（x﹣1）=3得﹣2x﹣2=3C．由得D．由得2x=﹣1210．根据如图中箭头的指向规律，从2014到2015再到2016，箭头的方向是以下图示中的（）A．B．C．D．二、填空题（本大题共6小题，每小题3分，满分18分）11．计算：|﹣2|=．12．单项式﹣5a2b的系数是．13．若x=2是关于x的方程2x+m=7的解，则m=．14．钟面上7点30分时，时针与分针的夹角的度数是．15．一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件原价的8折（即按照原价的80%）销售，售价为120元，则这款羊毛衫的原销售价为．16．已知：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…，根据前面各式的规律可猜测：101+103+105+…+199=．三、解答题（本大题共10小题，满分62分，解答应写出说理过程或演算步骤）17．计算：3+（﹣11）﹣（﹣9）18．计算：（﹣1）2016+（﹣16）÷22×．19．如图是由10个同样大小的小正方体搭成的几何体，请在上面方格纸中分别画出这个几何体从正面看、从左面看、从上面看的形状图；20．解方程：﹣=1．21．先化简，再求值：（2a2b﹣5ab+1）﹣（3ab+2a2b），其中a=﹣3，b=．22．某商场对今年双十一这天销售A、B、C三种品牌的电饭煲的情况进行了统计，绘制如图1和图2所示的统计图，根据图中信息解答下列问题：（1）A、B、C三种品牌的电饭煲总共销售了多少个？（2）补全图1中的条形统计图．（3）求出B品牌电饭煲在图2中所对应的圆心角的度数．23．对于有理数a、b定义一种新运算，规定a☆b=a2﹣ab．（1）求2☆（﹣3）的值；（2）若（﹣2）☆（3☆x）=4，求x的值．24．列一元一次方程解应用题：学生在素质教育基地进行社会实践活动，帮助农民伯伯采摘了黄瓜和茄子共80千克，了解到这些蔬菜的种植成本共180元，还了解到如下信息：（1）求采摘的黄瓜和茄子各多少千克？（2）这些采摘的黄瓜和茄子可赚多少元？25．将一副三角尺叠放在一起．（1）如图（1），若∠1=25°，求∠2的度数；（2）如图（2），若∠CAE=3∠BAD，求∠CAD的度数．26．在数轴上有A、B两点，所表示的数分别为n，n+6，A点以每秒5个单位长度的速度向右运动，同时B点以每秒3个单位长度的速度也向右运动，设运动时间为t秒．（1）当n=1时，则AB=；（2）当t为何值时，A、B两点重合；（3）在上述运动的过程中，若P为线段AB的中点，数轴上点C所表示的数为n+10是否存在t的值，使得线段PC=4，若存在，求t的值；若不存在，请说明理由．福建省三明市六县统考七年级（上）期末数学试卷参考答案与试题解析一、选择题（共10小题，每小题2分，满分20分每小题只有一个正确的选项）1．﹣9的相反数是（）A．B．﹣C．9D．﹣9【考点】14：相反数．【分析】根据只有符号不同的两个数互为相反数，可得一个数的相反数．【解答】解：﹣9的相反数是9，故选：C．2．计算（﹣2）×3的结果是（）A．﹣5B．﹣6C．1D．6【考点】1C：有理数的乘法．【分析】原式利用异号两数相乘的法则计算即可得到结果．【解答】解：原式=﹣2×3=﹣6，故选B3．下列说法正确的是（）A．射线PA和射线AP是同一条射线B．射线OA的长度是12cmC．直线ab、cd相交于点MD．两点确定一条直线【考点】IA：直线、射线、线段．【分析】根据射线的表示方法判断A；根据射线的定义判断B；根据直线的表示方法判断C；根据直线的性质公理判断D．【解答】解：A、射线PA和射线AP是同一条射线，说法错误；B、射线OA的长度是12cm，说法错误；C、直线ab、cd相交于点M，说法错误；D、两点确定一条直线，说法正确．故选D．4．下列问题，适合抽样调查的是（）A．了解一批灯泡的使用寿命B．学校招聘老师，对应聘人员的面试C．了解全班学生每周体育锻炼时间D．上飞机前对旅客的安检【考点】V2：全面调查与抽样调查．【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而且抽样调查得到的调查结果不准确，只是近似值．【解答】解：A、调查具有破坏性，适合抽样调查，故选项符合题意；B、人数不多，容易调查，且事关重大，必须全面调查，故选项不符合题意；C、班内人数不多，容易调查，适合全面调查，故选项不符合题意；D、事关重大，必须进行全面调查，故选项不符合题意．故选A．5．下面四个立体图形，从正面、左面、上面对空都不可能看到长方形的是（）A．B．C．D．【考点】U1：简单几何体的三视图．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．依此找到从正面、左面、上面观察都不可能看到长方形的图形．【解答】解：A、主视图为三角形，左视图为三角形，俯视图为有对角线的矩形，故本选项错误；B、主视图为等腰三角形，左视图为等腰三角形，俯视图为圆，从正面、左面、上面观察都不可能看到长方形，故本选项正确；C、主视图为长方形，左视图为长方形，俯视图为圆，故本选项错误；D、主视图为长方形，左视图为长方形，俯视图为长方形，故本选项错误．故选：B．6．经专家估算，南海属我国传统疆线以内的油气资源约合15000亿美元，用科学记数法表示数字15000是（）A．15×103B．1.5×103C．1.5×104D．1.5×105【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：用科学记数法表示数字15000是1.5×104，故选：C．7．下列运算正确的是（）A．x﹣3y=﹣2xy B．5x2﹣2x2=3x2C．x2+x3=x5D．2x2y﹣xy2=xy【考点】35：合并同类项．【分析】直接利用合并同类项法则化简判断求出答案．【解答】解：A、x﹣3y无法计算，故此选项不合题意；B、5x2﹣2x2=3x2，正确，符合题意；C、x2+x3无法计算，故此选项不合题意；D、2x2y﹣xy2无法计算，故此选项不合题意；故选：B．8．如图，数轴上有M，N，P，Q四个点，其中点P所表示的数为a，则数﹣3a所对应的点可能是（）A．M B．N C．P D．Q【考点】13：数轴．【分析】根据数轴可知﹣3a一定在原点的左边，且到原点的距离是点P到原点距离的3倍，即可解答．【解答】解：∵点P所表示的数为a，点P在数轴的右边，∴﹣3a一定在原点的左边，且到原点的距离是点P到原点距离的3倍，∴数﹣3a所对应的点可能是M，故选：A．9．下列方程的变形中正确的是（）A．由x+5=6x﹣7得x﹣6x=7﹣5B．由﹣2（x﹣1）=3得﹣2x﹣2=3C．由得D．由得2x=﹣12【考点】86：解一元一次方程．【分析】分别对所给的四个方程利用等式性质进行变形，可以找出正确答案．【解答】解：A、由x+5=6x﹣7得x﹣6x=﹣7﹣5，故错误；B、由﹣2（x﹣1）=3得﹣2x+2=3，故错误；C、由得=1，故错误；D、正确．故选D．10．根据如图中箭头的指向规律，从2014到2015再到2016，箭头的方向是以下图示中的（）A．B．C．D．【考点】37：规律型：数字的变化类．【分析】观察不难发现，每4个数为一个循环组依次循环，根据题意得出2015是第504个循环组的第3个数，2016是第504个循环组的第4个数，进而解答即可．【解答】解：由图可知，每4个数为一个循环组依次循环，2012÷4=503，故2013是第504个循环的第1个数，2014是第504个循环组的第2个数，2015是第504个循环组的第3个数，2016是第504个循环组的第4个数．故从2014到2015再到2016，箭头的方向是：．故选：C．二、填空题（本大题共6小题，每小题3分，满分18分）11．计算：|﹣2|=2．【考点】15：绝对值．【分析】根据绝对值定义去掉这个绝对值的符号．【解答】解：∵﹣2＜0，∴|﹣2|=2．故答案为：2．12．单项式﹣5a2b的系数是﹣5．【考点】42：单项式．【分析】单项式的系数时指数字因数．【解答】解：故答案为：﹣5，13．若x=2是关于x的方程2x+m=7的解，则m=3．【考点】85：一元一次方程的解．【分析】把x=2代入方程得到一个关于m的方程，解方程求得m的值．【解答】解：把x=2代入方程得4+m=7，解得m=3．故答案是：3．14．钟面上7点30分时，时针与分针的夹角的度数是45°．【考点】IG：钟面角．【分析】根据时针与分针相距的份数乘以每份的度数，可得答案．【解答】解：7点30分时，时针与分针的夹角的度数是30×（1+0.5）=45°，故答案为：45°15．一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件原价的8折（即按照原价的80%）销售，售价为120元，则这款羊毛衫的原销售价为150元．【考点】8A：一元一次方程的应用．【分析】此题的相等关系为，原价的80%等于销售价，依次列方程求解．【解答】解：设这款羊毛衫的原销售价为x元，依题意得：80%x=120，解得：x=150，故答案为：150元．16．已知：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…，根据前面各式的规律可猜测：101+103+105+…+199=7500．【考点】37：规律型：数字的变化类；1G：有理数的混合运算．【分析】根据题意知，从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方，用从1开始到199的奇数的和减去从1开始到99的奇数的和，列式计算即可得解．【解答】解：101+103+105+107+…+195+197+199=（）2﹣（）2；=1002﹣502，=10000﹣2500，=7500，故答案为：7500．三、解答题（本大题共10小题，满分62分，解答应写出说理过程或演算步骤）17．计算：3+（﹣11）﹣（﹣9）【考点】1B：有理数的加减混合运算．【分析】先把原式去括号，再按照从左到右的顺序计算即可，特别要注意去括号时符号的变化．【解答】解：3+（﹣11）﹣（﹣9）=3﹣11+9=﹣8+9=1．18．计算：（﹣1）2016+（﹣16）÷22×．【考点】1G：有理数的混合运算．【分析】原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：原式=1﹣16÷4×=1﹣1=0．19．如图是由10个同样大小的小正方体搭成的几何体，请在上面方格纸中分别画出这个几何体从正面看、从左面看、从上面看的形状图；【考点】U4：作图﹣三视图；U3：由三视图判断几何体．【分析】观察图形可知，从正面看到的图形是3列，左边一列是3个正方形，中间一列是1个正方形，右边一列是2个正方形在下面；从左面看到的图形是3列分别为3，2，1个正方形；从上面看到的图形是3列，分别3，2，1个正方形；据此即可画图．【解答】解：如图所示：20．解方程：﹣=1．【考点】86：解一元一次方程．【分析】方程去分母，去括号，移项合并，将x系数化为1，即可求出解．【解答】解：去分母得：4（2x+1）﹣3（x﹣2）=12，去括号得：8x+4﹣3x+6=12，移项合并得：5x=2，解得：x=．21．先化简，再求值：（2a2b﹣5ab+1）﹣（3ab+2a2b），其中a=﹣3，b=．【考点】45：整式的加减—化简求值．【分析】原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．【解答】解：原式=2a2b﹣5ab+1﹣3ab﹣2a2b=﹣8ab+1，当a=﹣3，b=时，原式=8+1=9．22．某商场对今年双十一这天销售A、B、C三种品牌的电饭煲的情况进行了统计，绘制如图1和图2所示的统计图，根据图中信息解答下列问题：（1）A、B、C三种品牌的电饭煲总共销售了多少个？（2）补全图1中的条形统计图．（3）求出B品牌电饭煲在图2中所对应的圆心角的度数．【考点】VC：条形统计图；VB：扇形统计图．【分析】（1）根据A品牌的销售量是400，所占的比例是即可求得销售的总个数；（2）利用销售的总个数减去其他品牌的个数即可求得B品牌的个数；（3）利用360度乘以对应的比例即可．【解答】解：（1）销售的总数是：400÷=2400（个）；（2）B品牌销售的个数：2400﹣400﹣1200=800（个）．；（3）B品牌电饭煲在图2中所对应的圆心角的度数是：360×=120°．23．对于有理数a、b定义一种新运算，规定a☆b=a2﹣ab．（1）求2☆（﹣3）的值；（2）若（﹣2）☆（3☆x）=4，求x的值．【考点】1G：有理数的混合运算；86：解一元一次方程．【分析】（1）根据☆的含义，以及有理数的混合运算的运算方法，求出2☆（﹣3）的值是多少即可．（2）首先根据☆的含义，以及有理数的混合运算的运算方法，由（﹣2）☆（3☆x）=4，列出一元一次方程，然后根据解一元一次方程方法，求出x的值是多少即可．【解答】解：（1）2☆（﹣3）=22﹣2×（﹣3）=4+6=10（2）（﹣2）☆（3☆x）=（﹣2）☆（9﹣3x）=（﹣2）2﹣（﹣2）×（9﹣3x）=22﹣6x=4解得x=3．24．列一元一次方程解应用题：学生在素质教育基地进行社会实践活动，帮助农民伯伯采摘了黄瓜和茄子共80千克，了解到这些蔬菜的种植成本共180元，还了解到如下信息：（1）求采摘的黄瓜和茄子各多少千克？（2）这些采摘的黄瓜和茄子可赚多少元？【考点】8A：一元一次方程的应用．【分析】（1）设采摘的黄瓜x千克，则茄子（80﹣x）千克，根据题意可得等量关系：黄瓜的成本+茄子的成本=180元，根据等量关系列出方程，再解即可；（2）根据（1）中的结果计算出黄瓜的利润和茄子的利润，再求和即可．【解答】解：（1）设采摘的黄瓜x千克，则茄子（80﹣x）千克，由题意得：2x+3（80﹣x）=180，解得：x=60，80﹣60=20（千克），答：采摘的黄瓜60千克，则茄子20千克；（2）（3﹣2）×60+（4﹣2.4）×20=60+32=92（元），答：采摘的黄瓜和茄子可赚92元．25．将一副三角尺叠放在一起．（1）如图（1），若∠1=25°，求∠2的度数；（2）如图（2），若∠CAE=3∠BAD，求∠CAD的度数．【考点】IL：余角和补角．【分析】（1）根据同角的余角相等即可得到结论；（2）设∠BAD=x°，则∠CAE=3x°，根据∠ECB+∠DAB=60°得出90﹣3x+x=60，求出x即可．【解答】解：（1）∵∠EAD=∠CAB=90°，∴∠1=90°﹣∠DAC，∠2=90°﹣CAD，∴∠1=∠2；（2）如图（2），设∠BAD=x°，则∠CAE=3x°，∵∠EAB+∠DAB=60°，∴90﹣3x+x=60，x=15，即∠BAD=15°，∴∠CAD=90°+15°=105°．26．在数轴上有A、B两点，所表示的数分别为n，n+6，A点以每秒5个单位长度的速度向右运动，同时B点以每秒3个单位长度的速度也向右运动，设运动时间为t秒．（1）当n=1时，则AB=|2t﹣6|；（2）当t为何值时，A、B两点重合；（3）在上述运动的过程中，若P为线段AB的中点，数轴上点C所表示的数为n+10是否存在t的值，使得线段PC=4，若存在，求t的值；若不存在，请说明理由．【考点】8A：一元一次方程的应用；13：数轴．【分析】找出运动时间为t秒时，点A、B表示的数．（1）将n=1代入点A、B表示的数中，再根据两点间的距离公式即可得出结论；（2）根据点A、B重合即可得出关于t的一元一次方程，解之即可得出结论；（3）根据点A、B表示的数结合点P为线段AB的中点即可找出点P表示的数，根据PC=4即可得出关于t的一元一次方程，解之即可得出结论．【解答】解：当运动时间为t秒时，点A表示的数为5t+n，点B表示的数为3t+n+6．（1）当n=1时，点A表示的数为5t+1，点B表示的数为3t+7，AB=|5t+1﹣（3t+7）|=|2t﹣6|．故答案为：|2t﹣6|．（2）根据题意得：5t+n=3t+n+6，解得：t=3．∴当t为3时，A、B两点重合．（3）∵P为线段AB的中点，∴点P表示的数为（5t+n+3t+n+6）÷2=4t+n+3，∵PC=4，∴|4t+n+3﹣n﹣10|=|4t﹣7|=4，解得：t=或t=．∴存在t的值，使得线段PC=4，此时t的值为或．。

福建省三明市七年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题（每小题3分，共30分） (共10题；共30分)1. （3分）(2017·嘉兴模拟) a的相反数是（）A . |a|B .C . ﹣aD .2. （3分）在，，，3.1415926，2+，3.212212221…，这些数中，无理数的个数为（）A . 2B . 3C . 4D . 53. （3分） (2020七上·椒江期末) 2019年10月1日，中华人民共和国在北京天安门举行了盛大的建国70周年庆典活动。

据统计，参加阅兵和群众游行的人数大约有12万人，12万用科学记数法表示为（）A .B .C .D .4. （3分）若 =25, =3,则a+b=（）A . -8B . ±8C . ±2D . ±8或±25. （3分） (2016高一下·锦屏期末) 某种品牌的彩电降价30%以后，每台售价为a元，则该品牌彩电每台原价为（）A . 0. 7a元B . 0. 3a元C . 元D . 元6. （3分）下列说法中：①过两点有且只有一条直线；②两点之间选段最短；③在平面内有一点P使得PA=PB，那么，点P就是线段AB的中点；④连接两点的线段叫两点之间的距离；其中正确的有（）A . 1个B . 2个C . 3个D . 4个7. （3分）线段AB上有点C，点C使AC:CB=2:3，点M和点N分别是线段AC和线段CB的中点，若MN=4，则AB的长是（）A . 6；B . 8；C . 10；D . 128. （3分）已知∠AOC=∠BOD=90°，∠AOB=170°，则∠DOC=（）A . 40°B . 30°C . 20°D . 10°9. （3分）(2019七上·靖远月考) 对于实数a，b，c，d，规定一种运算，如，那么当时，x等于（）A .B .C .D .10. （3分） (2020七上·南浔期末) 有一个魔术，魔术师背对小聪，让小聪拿着扑克牌按下列四个步骤操作：①第一步：分发左、中、右三堆牌，每堆牌不少于五张，且各堆牌的张数相同；②第二步：从左边一堆拿出五张，放入中间一堆；③第三步：从右边一堆拿出三张，放入中间一堆；④第四步：右边一堆有几张牌，就从中间一堆拿几张牌放入右边一堆。

福建省三明市2020版七年级上学期数学期末考试试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题；共12分)1. （2分） -3的倒数是（）A . 3B .C .D . -32. （2分） (2015七上·罗山期中) 钓鱼岛是我国固有领土，位于我国东海，总面积约6340000平方米，数据6340000用科学记数法表示为（）A . 634×104B . 6.34×106C . 63.4×105D . 6.34×1073. （2分）(2017·永定模拟) 如图是某个几何体的三视图，则该几何体的形状是（）A . 长方体B . 圆锥C . 圆柱D . 三棱柱4. （2分） (2019七上·诸暨期末) 下列计算正确的是（）A .B .C .D .5. （2分） (2017九上·东丽期末) 若关于的一元二次方程的一个根是，则的值是（）A .B .C .D .6. （2分）(2019·吴兴模拟) 如图，将长BC=8cm，宽AB=4cm的矩形纸片ABCD折叠，使点C与点A重合，则折痕EF的长为（）A . 4cmB . cmC . cmD . c二、填空题 (共10题；共20分)7. （1分） (2020七上·咸阳月考) 写出所有大于而小于的整数________.8. （1分） (2017八下·蚌埠期中) 比较大小： ________ ．（填“＞”、“=”、“＜”）．9. （1分） (2019七上·慈利期中) 某微商平台有一商品，标价为a元，按标价的6折再降价20元销售，则该商品售价用代数式表示为________元.10. （2分） (2018七上·江海期末) 单项式的系数是________，次数是________11. （1分） (2018八上·开封期中) 等腰三角形的周长为13cm ，其中一边长为3cm ，则底边长等于________cm.12. （1分） (2019七上·宝应期末) 已知a-3b=2，则（3b-a）2+4（a-3b）-17=________.13. （1分）某公园划船项目收费标准如下：船型两人船（限乘两人）四人船（限乘四人）六人船（限乘六人）八人船（限乘八人）每船租金（元/小时）90100130150某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为________元．14. （1分） (2020八上·仙居期中) 如图是一枚“八一”建军节纪念章，其外轮廓是一个正五边形，则图中∠1的大小为________°.15. （1分） (2018七上·重庆月考) 如图，：：：7：4，OM平分，，则的度数为________度16. （10分） (2019七下·大名期中) 如图，E点为DF上的点，B为AC 上的点，∠1=∠2，∠C=∠D求证：DF∥AC证明：∵ ∠1=∠2（已知），∠1=∠3 ，∠2=∠4（________），∴ ∠3=∠4（ ________），∴ ________∥________（ ________ ）．∴∠C=∠ABD（ ________ ）．∵∠C=∠D（________），∴ ∠D =________（ ________）．∴ DF∥AC（________）．三、解答题 (共10题；共87分)17. （10分） (2019七上·文昌期末) 计算：（1）（2）18. （5分） (2019七下·延庆期末) 计算：（x+3）（x﹣2）﹣（x﹣4）2 ．19. （5分）解方程：14.5+（x﹣7）=x+0.4（x+3）20. （15分）(2017·仪征模拟) 阅读下面材料：实际问题：如图（1），一圆柱的底面半径为5厘米，BC是底面直径，高AB为5厘米，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线．解决方案：路线1：侧面展开图中的线段AC，如图（2）所示，设路线l的长度为l1：则l12=AC2=AB2+BC2=52+（5π）2=25+25π2；路线2：高线AB+底面直径BC，如图（1）所示．设路线2的长度为l2：则l22=（AB+BC）2=（5+10）2=225．为比较l1 ， l2的大小，我们采用“作差法”：∵l12﹣l22=25（π2﹣8）＞0∴l12＞l22∴l1＞l2 ，小明认为应选择路线2较短．（1）问题类比：小亮对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为1厘米，高AB为5厘米．”．请你用上述方法帮小亮比较出l1与l2的大小：（2）问题拓展：请你帮他们继续研究：在一般情况下，当圆柱的底面半径为r厘米时，高为h厘米，蚂蚁从A点出发沿圆柱表面爬行到点C，当满足什么条件时，选择路线2最短？请说明理由．（3）问题解决：如图（3）为2个相同的圆柱紧密排列在一起，高为5厘米，当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时，求圆柱的底面半径r．（注：按上面小明所设计的两条路线方式）．21. （7分）如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，∠CBF=20°．（1）∠ACB的大小=________（度）；（2）求证：△ABE≌△ADE；（3）∠AED的大小=________（度）．22. （5分）将4个数a、b、c、d排成2行2列，两边各加一条竖直线记成，定义 =ad﹣bc，上述记号就叫做2阶行列式．若 =﹣20，求x的值．23. （5分）(2019·长春模拟) 自农村义务教育学生营养餐改善计划开展以来，某校七年级（d）班某天早上分到牛奶、面包共7件，每件牛奶24元，每件面包16元，共14元，该班分到牛奶、面包各多少件？24. （15分）如图1，直线x⊥y，垂足为O，A、B两点同时从点O出发，点A以每秒x个单位长度沿直线x 向左运动，点B以每秒y个单位长度沿直线y向上运动．（1）若|x+2y﹣5|+|2x﹣y|=0，试分别求出1秒钟后，线段OA、OB的长．（2）如图2，设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P．问：点A、B在运动的过程中，∠P 的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．（3）如图3，延长BA至E，在∠ABO的内部作射线BF交x轴于点C，若∠EAC、∠FCA、∠ABC的平分线相交于点G，过点G作BE的垂线，垂足为H，试问∠AGH和∠BGC的大小关系如何？请写出你的结论并说明理由．25. （15分）(2017·深圳模拟) 如图所示, 中，∠BAC=90°，∠C=30°，BC=2，⊙O是△ABC的外接圆，D是CB延长线上一点，且BD=1，连接DA，点P是射线DA上的动点。

福建省三明市2020版七年级上学期数学期末考试试卷（II）卷姓名:________ 班级:________ 成绩:________一、单选题 (共11题；共11分)1. （1分）下列计算中,错误的是（）A . (2xy)3(-2xy)2=32x5y5B . (-2ab2)2(-3a2b)3=-108a8b7C . =x4y3D . = m4n42. （1分）如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A . 90°B . 135°C . 270°D . 315°3. （1分）(2018·恩施) 在下列图形中，既是轴对称图形又是中心对称图形的是（）A .B .C .D .4. （1分）(2016·崂山模拟) 下列计算正确的是（）A . 4a2﹣2a2=2B . 3a+a=3a2C . 4a6÷2a3=2a2D . ﹣2a•a=﹣2a25. （1分） (2016七上·瑞安期中) 如图，一个瓶子的容积为1L,，瓶内装着一些溶液. 当瓶子正放时，瓶内溶液的高度为30cm，将瓶子倒放时，空余部分的高度为10cm. 现将瓶内的溶液全部倒入一个圆柱形的杯子里，杯内溶液的高度为15cm，则圆柱形杯子的内底面半径约为（）A . 2..8cmB . 4.0cmC . 5.0cmD . 6.2cm6. （1分）当a=﹣1时，分式（）A . 等于零B . 等于1C . 等于﹣1D . 没有意义7. （1分）下列分式是最简分式的是（）A .B .C .D .8. （1分）下列多项式能用完全平方公式分解的是（）A . x2－2x－B . (a＋b) (a－b)－4aC . a2＋ab＋D . y2＋2y－19. （1分） (2018九上·郑州开学考) 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（）A .B . 2C .D . 310. （1分）如图，菱形ABCD中，AB=AC，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O．则下列结论：①△ABF≌△CAE，②∠AHC=120°，③AH+CH=DH，④AD2=OD•DH中，正确的是（）A . ①②④B . ①②③C . ②③④D . ①②③④11. （1分）某超市用240元购进的新上市水果迅速售完，第二次又用300元对外购进这种水果若干．已知第二次的进价比第一次进价每千克优惠2元，结果比第一次多买进20千克．求第一次的进价为多少元？若设第一次购买水果的进价为x元，则可列方程为A .B .C .D .二、填空题 (共4题；共4分)12. （1分）因式分解：2x3﹣8x=________13. （1分）(2017·岳池模拟) 如果分式的值为零，那么x=________．14. （1分）(2014·扬州) 如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A=65°，则∠DOE=________．15. （1分）如图，在平面直角坐标系中，点P在函数y=（x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结PC并延长交x轴于点D．则△APD的面积为________.三、解答题 (共8题；共10分)16. （1分） (2016八上·东营期中) 先化简，再求值：[（x﹣2y）2﹣（﹣x﹣2y）（﹣x+2y）]÷（﹣4y），其中x和y的取值满足 +（x2+4xy+4y2）=0．17. （1分） (2018八上·仙桃期末)（1）计算：（12a3－6a2＋3a）÷3a；（2）解方程： .18. （1分）先化简，再求值：，其中．19. （1分）(2017·泰兴模拟)（1）计算：（﹣2）0﹣（﹣1）2017+ ﹣sin45°；（2）化简：（﹣）÷ ．20. （1分） (2017八下·汇川期中) 在正方形ABCD中，CE=DF，求证：AE⊥BF．21. （1分）如图，E，C是线段BF上的两点，BE=FC，AB∥DE，∠A=∠D，AC=6，求DF的长．22. （1分） (2020八下·曹县月考) 某市为创建全同文明城市，开展了“美化绿化城市“活动，计划经过若干年使城区绿化总面积新增360万平方米，自2014年初开始实施后．实际每年的绿化面积是原计划的1.6倍，这样可提前4年完成任务，求实际每年绿化的面积是多少万平方米?23. （3分） (2019七下·重庆期中) 如图1，在平面直角坐标系中，点A（a，0），B（b，3），C（c，0），满足 + + =0.（1）分别求出点，，的坐标及三角形ABC的面积.（2）如图2.过点C作于点D，F是线段AC上一点，满足，若点G是第二象限内的一点，连接DG，使，点E是线段AD上一动点（不与A、D重合），连接CE交DF于点H，点E在线段AD上运动的过程中，的值是否会变化？若不变，请求出它的值；若变化，请说明理由.（3）如图3，若线段AB与轴相交于点F，且点F的坐标为（0，），在坐标轴上是否存在一点P，使三角形ABP和三角形ABC的面积相等？若存在，求出P点坐标.若不存在，请说明理由.（点C除外）参考答案一、单选题 (共11题；共11分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、二、填空题 (共4题；共4分)12-1、13-1、14-1、15-1、三、解答题 (共8题；共10分)16-1、17-1、17-2、18-1、19-1、19-2、20-1、21-1、22-1、23-1、23-2、23-3、。

福建省三明市2020版七年级上学期数学期末考试试卷（II）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共12分)1. （1分）的绝对值是（）A . ﹣B .C . ﹣6D . 62. （1分） (2017九下·潍坊开学考) 下列计算正确的是（）A . x3﹣x2=xB . x3•x2=x6C . x3÷x2=xD . （x3）2=x53. （1分）如图放置的圆柱体的左视图为（）A .B .C .D .4. （1分）下列通过移项变形，错误的是（）A . 由x+2=2x-7，得x-2x=-7-2B . 由x+3=2-4x，得x+4x=2-3C . 由2x-3+x=2x-4，得 2x-x-2x=-4+3D . 由1-2x=3，得-2x=3-15. （1分） (2019七上·咸阳期中) 下列说法正确的是（）A . 的系数是B . 单项式的系数为，次数为C . 次数为次D . 的系数为6. （1分） (2020七上·甘州期末) 有如下说法：①直线是一个平角；②如果线段AB＝BC，则B是线段AC 的中点；③射线AB与射线BA表示同一射线；④用一个扩大2倍的放大镜去看一个角，这个角扩大2倍；⑤两点之间，直线最短；⑥120.5°＝120°30′，其中正确的有（）A . 1个B . 2个C . 3个D . 4个7. （1分）如果ax2+24x+b=(mx-3)2,那么（）A . a=16,b=9,m=-4B . a=64,b=9,m=-8C . a=-16,b=-9,m=-8D . a=16,b=9,m=48. （1分） (2019七上·朝阳期末) 如图，直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交，若∠1＝30°，则∠2的度数是（）A . 30°B . 45°C . 60°D . 75°9. （1分）如果，则等于（）A .B . xyC . 4D .10. （1分）﹣7的相反数是（）A . -B . -7C .D . 711. （1分）某人用x元钱买年利率为2.89%的5年期国库券，5年后本息和为2.1万元，则列出方程得（）A . x+x×5×2.89%=2.1B . x×5×2.89%=21000C . x×5×2.89%=2.1D . x+x×5×2.89%=2100012. （1分）一条船在一条河上的顺流航速是逆流航速的3倍，这条船在静水中的航速与河水的流速之比为（）A . 3：1B . 2：1C . 1:1D . 3:2二、填空题 (共5题；共5分)13. （1分） (2017七上·渭滨期末) 数、、在数轴上对应点的位置如图所示，则________；14. （1分）(2018·阿城模拟) 2018年春节黄金周,哈尔滨太平国际机场运送旅客约430000人次,创历史新高,请将430000用科学记数法表示为________.15. （1分） (2016七上·孝义期末) 已知线段AB=10cm，直线AB上有一点C，BC=4cm，则线段AC=________cm．16. （1分）某班同学利用假期参加夏令营活动，分成几个小组，若每组7人还余1人；若每组8人还缺少6人．若设该班分成x个小组，可列方程为________ ．17. （1分）时钟的时针在不停地旋转，从下午3时到下午6时（同一天），时针旋转的角度是________．三、解答题 (共7题；共14分)18. （2分） (2018七上·平顶山期末) 计算：（1） -0.5+|-22-4|÷(-4)（2） -22÷ (1- )219. （1分）如图，已知A、B、C、D是正方形网格纸上的四个格点，根据要求在网格中画图并标注相关字母．画线段AB；画直线AC；过点D画AC的垂线，垂足为E；在直线AC上找一点P，使得PB+PD最小．20. （1分） (2018七上·沙洋期末) 若有理数a、b、c在数轴上对应的点A、B、C位置如图，化简．21. （2分） (2019七上·惠山期中)（1）先化简再求值：，其中a、b满足（2）已知a＋b＝4，ab＝－2，求代数式(5a－4b－4ab)－3(a－2b－ab)的值．22. （2分） (2019八上·海安期中) 如图1，已知中，点在边上，交边于点，且平分 .（1）求证：；（2）如图2，在边上取点，使，若，，求的长。

福建省三明市2020版七年级上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2017·南山模拟) 下列四个数中，最大的数是（）A . ﹣2B .C . 0D . 62. （2分）冬季的一天室内温度是12℃，室外是 -2℃,则室内外温度相差是（）A . 14℃B . 12℃C . 10℃D . 2℃3. （2分）(2019·邹平模拟) 2018年我国在人工智能领域取得显著成就，自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军，这得益于所建立的大数据中心的规模和数据存储量，它们决定着人工智能深度学习的质量和速度，其中的一个大数据中心能存储58000000000本书籍．将58000000000用科学记数法表示应为（）A . 58×109B . 5．8×1010C . 5．8×1011D . 0．58×10114. （2分） (2019七上·泰兴月考) 如果向北走8km记作+8km，那么-5km表示（）A . 向北走5kmB . 向南走-5kmC . 向东走5kmD . 向南走5km5. （2分）(2017·赤壁模拟) 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM．若∠AOC=70°，则∠CON的度数为（）A . 65°B . 55°C . 45°D . 35°6. （2分） (2019七上·道外期末) 下列所给的方程变形中，正确的是（）A . 把方程移项得B . 把方程去括号得C . 若，则D . 方程去分母得7. （2分） (2018七上·青山期中) 下列计算正确的是（）A . 2a+b＝3abB . 2b3+3b3＝5b6C . 6a3﹣2a3＝4D . 5a2b﹣4a2b＝a2b8. （2分）(2019·南山模拟) 下列计算正确的是（）A . （a+b）2＝a2+b2B . （﹣2a2）2＝﹣4a4C . a5÷a3＝a2D . a4+a7＝a119. （2分） 2010年“地球停电一小时”活动的某地区烛光晚餐中，设座位有x排，每排坐30人，则有8人无座位；每排坐31人，则空26个座位，则下列方程正确的是（）A . 30x－8＝31x＋26B . 30x＋8＝31x＋26C . 30x－8＝31x－26D . 30x＋8＝31x－2610. （2分）在墙壁上固定一根横放的木条，则至少需要钉子的枚数是（）A . 1B . 2C . 3D . 411. （2分）若∠A=45°18′，∠B=45°15′30″，∠C=45.15°，则（）A . ∠A＞∠B＞∠CB . ∠B＞∠A＞∠CC . ∠A＞∠C＞∠BD . ∠C＞∠A＞∠B12. （2分）下列计算正确的是（）A .B .C .D .二、填空题 (共10题；共13分)13. （1分）(2017·衡阳模拟) 根据科学家估计，地球年龄大约是4 600 000 000年，这个数用科学记数法表示为________．14. （1分） (2018七上·佳木斯期中) 如果某天的最高气温是5℃，最低气温是﹣3℃，那么日温差是________℃．15. （2分） (2018七上·高阳期末) 如图，O是线段AB上一点，E、F分别是AO、OB的中点，若EF=3，AO=2，则OB=________．16. （1分） (2020七上·临颍期末) 已知线段，点是直线上一点，且，若点是线段的中点，点是线段的中点，则线段 ________ .17. （1分） (2015九上·莱阳期末) 圆锥的底面半径为5，侧面积为60π，则其侧面展开图的圆心角等于________．18. （1分）计算：15°37′+42°51′=________19. （2分）如图，OA⊥OC，OB⊥OD，下面结论：①∠AOB=∠COD；②∠AOB+∠COD=90°；③∠BOC+∠AOD=180°；④∠AOC-∠COD=∠BOC中，正确的有________ （填序号）．20. （2分）某兴趣小组从学校出发骑车去植物园参观，先经过一段上坡路后到达途中一处景点，停车10分钟进行参观，然后又经一段下坡路到达植物园，行程情况如图，若他们上、下坡路速度不变，则这个兴趣小组的同学按原路返回所用的时间为________ 分钟（途中不停留）21. （1分）(2018·咸安模拟) 如图，已知点A1 ， A2 ，…，An均在直线y=x﹣1上，点B1 ， B2 ，…，Bn均在双曲线y=﹣上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，AnBn⊥x轴，BnAn+1⊥y 轴，…，记点An的横坐标为an（n为正整数）．若a1=﹣1，则a2016=________．22. （1分）某品牌电脑进价为5 000元，按照定价的9折销售时，获利760元，则此电脑的定价为________元．三、解答题 (共5题；共27分)23. （10分）用四舍五入法，按括号里的要求对下列各数取近似值：（1）0.65148（精确到千分位）（2）1.5673（精确到0.01）（3）450600（精确到千位）24. （5分） (2017七上·龙湖期末) 把一批书分发给某班的学生，若每名学生发3本书，则剩余20本书；若每名学生发4本书，则还少25本书．问这个班级有多少名学生？这批书有多少本？25. （5分）化简求值:2（x2y+xy）-3（x2y-xy）-4x2y,其中x=1,y=-1．26. （5分）从甲地到乙地，某人骑自行车比乘公共汽车多用2.5h，已知骑自行车的平均速度为每小时15km，公共汽车的平均速度为每小时40km，求甲乙两地之间的路程（只列方程）．27. （2分） (2018七下·韶关期末) 在平面直角坐标系中，A（﹣2，0），C（2，2），过C作CB⊥x轴于B．（1）如图1，△ABC的面积是________；（2）如图1，在y轴上找一点P，使得△ABP的面积与△ABC的面积相等，请直接写出P点坐标：________；（3）如图2，若过B作BD∥AC交y轴于D，则∠BAC+∠ODB的度数为________度；（4）如图3，BD∥AC，若AE、DE分别平分∠CAB，∠ODB，求∠AED的度数．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共10题；共13分)13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、21-1、22-1、三、解答题 (共5题；共27分) 23-1、23-2、23-3、24-1、25-1、26-1、27-1、27-2、27-3、27-4、。