123角的平分线的性质课后训练

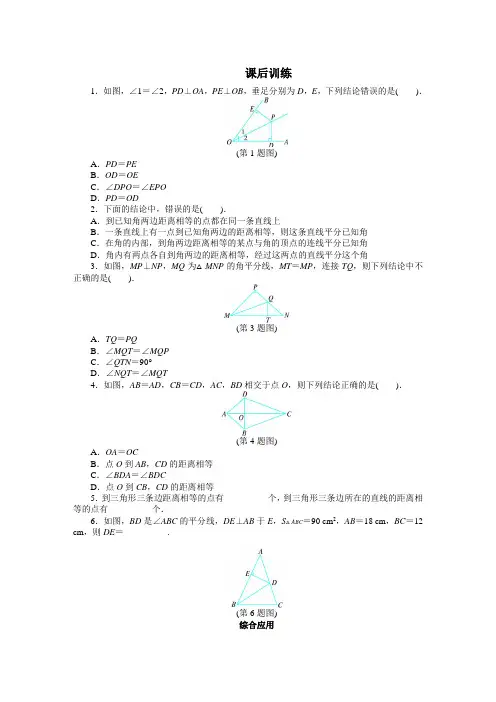
课后训练1．如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是()．(第1题图)A．PD＝PEB．OD＝OEC．∠DPO＝∠EPOD．PD＝OD2．下面的结论中，错误的是()．A．到已知角两边距离相等的点都在同一条直线上B．一条直线上有一点到已知角两边的距离相等，则这条直线平分已知角C．在角的内部，到角两边距离相等的某点与角的顶点的连线平分已知角D．角内有两点各自到角两边的距离相等，经过这两点的直线平分这个角3．如图，MP⊥NP，MQ为△MNP的角平分线，MT＝MP，连接TQ，则下列结论中不正确的是()．(第3题图)A．TQ＝PQB．∠MQT＝∠MQPC．∠QTN＝90°D．∠NQT＝∠MQT4．如图，AB＝AD，CB＝CD，AC，BD相交于点O，则下列结论正确的是()．(第4题图)A．OA＝OCB．点O到AB，CD的距离相等C．∠BDA＝∠BDCD．点O到CB，CD的距离相等5．到三角形三条边距离相等的点有__________个，到三角形三条边所在的直线的距离相等的点有__________个．6．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝90 cm2，AB＝18 cm，BC＝12 cm，则DE＝__________.(第6题图)综合应用7．如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC.求证：(1)AM平分∠DAB；(2)∠DMA＝90°.(第7题图)8．如图，BE⊥AC于E，CF⊥AB于F，BE，CF相交于点D，且BD＝CD.求证：∠BAD ＝∠CAD.(第8题图)9．现有一块形状为三角形的闲地，其三边的长分别为20 cm,30 cm,40 cm，现要把它分成面积比为2∶3∶4的三部分，分别种植不同的花草，请你设计一种方案，并简单说明理由．参考答案1.答案：D点拨：由角的平分线的性质易知PD＝PE，易证△PEO≌△PDO，所以有OD＝OE，∠DPO＝∠EPO.2.答案：B点拨：某点到角两边的距离相等，只能说明该点在角的平分线上，而过该点的直线有无数条，要确定角的平分线还需要一个点．3.答案：D点拨：由SAS易证△PMQ≌△TMQ，所以TQ＝PQ，∠MQT＝∠MQP，∠P＝∠MTQ＝90°，则∠QTN＝90°，可得选项A，B，C正确．故选D.4.答案：D点拨：由SSS可证△ABC≌△ADC，∴∠ACD＝∠ACB，∴点O在∠BCD 的平分线上．所以选项D正确．5.答案：14点拨：在三角形外部，两相邻外角的平分线的交点到各边所在的直线的距离相等，这样的点在三角形外部有3个，在三角形内部有1个，共4个．6.答案：6 cm点拨：如图，作DF⊥BC于F，由角平分线的性质，可令DE＝DF＝h cm，则S△ABC＝S△ABD＋S△BCD，即\f(1,2)×18×h＋\f(1,2)×12×h＝90，所以h＝6，即DE＝6 cm.(第6题图)7.答案：证明：(1)如图，作MN⊥AD于点N∵DM平分∠ADC，∴由角平分线的性质，可知MC＝MN.又∵M是BC的中点，∴BM＝CM.∴NM＝BM.∴点M在∠DAB的平分线上．∴AM平分∠DAB.(2)由(1)知，DM平分∠ADC，(第7题图)∴∠ADM ＝21∠ADC . 又∵AM 平分∠DAB ， ∴∠DAM ＝21∠DAB . 又∵∠B ＝∠C ＝90°，∴∠B ＋∠C ＝180°，∴AB ∥CD .∴∠DAB ＋∠ADC ＝180°.∴∠ADM ＋∠DAM ＝21 (∠ADC ＋∠DAB )＝21×180°＝90°. ∴∠DMA ＝90°.点拨：有垂线段和角平分线时，我们一般考虑用角平分线的性质及其逆用来解决有关问题．8. 答案：证明：∵BE ⊥AC 于E ，CF ⊥AB 于F ，∴∠DFB ＝∠DEC ＝90°.在△DBF 和△DCE 中，⎪⎩⎪⎨⎧==︒==,，∠∠，90E ∠∠CD BD CDE BDF DC DFB ∴△BDF ≌△CDE (AAS)．∴DF ＝DE .又DF ⊥AB ，DE ⊥AC ，∴AD 是∠BAC 的平分线，∴∠BAD ＝∠CAD .点拨：证角相等有两种方法：(1)证两个角所在的两个三角形全等；(2)利用角平分线性质的逆用．结合具体图形选择合适的方法．9. 答案：解：如图，AC ＝20 cm ，BC ＝30 cm ，AB ＝40 cm ，作出该三角形空地△ABC 的三个内角的角平分线，交点为P ，连接P A ，PB ，PC ，则S △ACP ∶S △BCP ∶S △ABP ＝2∶3∶4.理由：作PD ⊥AB 于D ，PF ⊥AC 于F ，PE ⊥BC 于E ，由角平分线的性质，可知PD ＝PE ＝PF ，∴S △ACP ∶S △BCP ∶S △ABP ＝(21PF ·AC )∶(21PE ·CB )∶(21PD ·AB )＝AC ∶BC ∶AB ＝2∶3∶4.(第9题图)点拨：若已知三角形角平分线的交点到三边的距离为r ，则连接该交点与三角形各顶点构成的三个小三角形的面积的比就等于原三角形各边的比．。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！《12.3角平分线的性质》课时练一、选择题1．如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD＝6，则点P到边OB的距离为（）A．6B．5C．4D．32．△ABC是一个任意三角形，用直尺和圆规作出∠A、∠B的平分线，如果两条平分线交于点O，那么下列选项中不正确的是（）A．点O一定在△ABC的内部B．∠C的平分线一定经过点OC．点O到△ABC的三边距离一定相等D．点O到△ABC三顶点的距离一定相等3．如图，在Rt△ABC中，∠A＝90°，∠ABC的平分线BD交AC于点D，AD＝3，BC＝10，则△BDC的面积是（）A．10B．15C．20D．304．如图，在四边形ABCD中，AB＝CD，BA和CD的延长线交于点E，若点P使得S△P AB ＝S，则满足此条件的点P（）△PCDA．有且只有1个B．有且只有2个C．组成∠E的角平分线D．组成∠E的角平分线和外角平分线所在的直线（E点除外）5．如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于（）A．10B．7C．5D．46．下列作图语句正确的是（）A．以点O为顶点作∠AOBB．延长线段AB到C，使AC＝BCC．作∠AOB，使∠AOB＝∠αD．以A为圆心作弧7．如图，∠MON＝60°，OP平分∠MON，P A⊥ON于点A，点Q是射线OM的一个动点，若OP＝4，则PQ的最小值为（）A．B．4C．2D．8．如图，若OP平分∠AOB，PM⊥OA于M点，PM＝3，N是OB上一个动点，线段PN 的最小值是（）A．2B．3C．4D．59．如图，在△ABC中，∠C是直角，AD平分∠BAC，交BC于点D；如果AB＝8，CD＝2，那么△ABD的面积等于（）A．4B．6C．8D．1010．如图，已知AD∥BC，AP平分∠DAB，BP平分∠ABC，点P恰好在CD上，王玲同学根据给定的条件写出了四个结论：①AP⊥BP；②点P到AD，BC的距离相等；③PD＝PC；④AD+BC＝AB，其中结论正确的个数有（）A．1个B．2个C．3个D．4个二．填空题11．如图，△ABC中，∠BAC的角平分线交BC于D，过D作AC的垂线DE交AC于E，DE＝5，则D到AB的距离是．12．如图，在直角坐标系中，AD是Rt△OAB的角平分线，已知点D的坐标是（0，﹣3），AB的长是10，则△ABD的面积为．13．在数学活动课上，小明提出这样一个问题：如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC，∠CED＝35°，则∠EAB的度数是．14．如图△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，给出下列结论：①DC＝DE；②DA平分∠CDE；③DE平分∠ADB；④BE+AC＝AB；⑤∠BAC＝∠BDE．其中正确的是（写序号）15．如图，△ABC中，∠ABC与∠ACB的外角平分线交于P，PM⊥AC于M，若PM＝6cm，则点P到AB的距离为．三．解答题16．如图，在△ABC中，∠ABC＝90°，D为BC上一点，在△ADE中，∠E＝∠C，∠1＝90°﹣∠EDC．求证：（1）∠1＝∠2；（2）ED＝BC+BD．17．已知，如图，BD⊥AM于点D，CE⊥AN于点E，BD、CE交点F，CF＝BF，求证：点F在∠A的平分线上．18．已知：如图，∠AOC＝∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为点D、E．求证：PD＝PE．19．如图①，在△ABC中，∠ACB是直角，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，且FG⊥AB于G，FH⊥BC于H．（1）求证：∠BEC＝∠ADC；（2）请你判断并FE与FD之间的数量关系，并证明；（3）如图②，在△ABC中，如果∠ACB不是直角，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请问，你在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．参考答案一、选择题1．A2．D3．B4．D5．C6．C7．C8．B9．C10．D 二、填空题11．512．1513．35°14．①②④⑤15．6cm三、解答题16．证明：（1）由三角形的外角性质，∠BAD+∠ABD＝∠1+∠EDC，∵∠1＝90°﹣∠EDC，∴∠BAD+90°＝90°﹣∠EDC，∴∠BAD＝∠EDC，延长DB至F，使BF＝BD，则AB垂直平分DF，∴∠BAD＝∠DAF，AD＝AF，∴∠DAF＝∠EDC，∠2＝∠F，在△ADF中，∠F+∠DAF＝∠1+∠EDC，∴∠1＝∠F，∴∠1＝∠2；（2）在△AED和△ACF中，，∴△AED≌△ACF（AAS），∴ED＝CF，∵CF＝BC+BF＝BC+DB，∴ED＝BC+BD．17．证明：∵BD⊥AM，CE⊥AN，∴∠CDF＝∠BEF＝90°，在△CDF和△BEF中，，∴△CDF≌△BEF（AAS），∴DF＝EF，∴点F在∠A的平分线上．18．解：（1）角平分线上的点到该角两边的距离相等；（2）∵PD⊥OA，PE⊥OB，∴∠PDO＝∠PEO＝90°，在△PDO和△PEO中，，∴△PDO≌△PEO（AAS），∴PD＝PE．19．解：（1）∵AD、CE分别是∠BAC、∠BCA的平分线，∴∠DAC＝∠DAB＝∠BAC＝15°，∠ACE＝∠ACB＝45°，∴∠CDA＝∠BAD+∠ABD＝75°，∠BEC＝∠BAC+∠ECA＝75°，∴∠BEC＝∠ADC；（2）相等，理由：如图①，过点F作FH⊥BC于H．作FG⊥AB于G，连接BF，∵F是角平分线交点，∴BF也是角平分线，∴HF＝FG，∠DHF＝∠EGF＝90°，∵在Rt△ABC中，∠ACB＝90°，∠ABC＝60°，∴∠BAC＝30°，∴∠DAC＝∠BAC＝15°，∴∠CDA＝75°，∵∠HFC＝45°，∠HFG＝120°，∴∠GFE＝15°，∴∠GEF＝75°＝∠HDF，在△DHF和△EGF中，，∴△DHF≌△EGF（AAS），∴FE＝FD；（3）成立．理由：如图②，过点F作FM⊥BC于M．作FN⊥AB于N，连接BF，∵F是角平分线交点，∴BF也是角平分线，∴MF＝FN，∠DMF＝∠ENF＝90°，∴四边形BNFM是圆内接四边形，∵∠ABC＝60°，∴∠MFN＝180°﹣∠ABC＝120°，∵∠CF A＝180°﹣（∠F AC+∠FCA）＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠ABC）＝180°﹣（180°﹣60°）＝120°，∴∠DFE＝∠CF A＝∠MFN＝120°．又∵∠MFN＝∠MFD+∠DFN，∠DFE＝∠DFN+∠NFE，∴∠DFM＝∠NFE，在△DMF和△ENF中。

肓 最大最全最精的教育资源网 C.ABvAD+BCD.无法确定温馨提示： 此套题为Word 版，请按住Ctrl,滑动鼠标滚轴，调节合 适的观看比例，答案解析附后。

关闭Word 文档返回原板块。

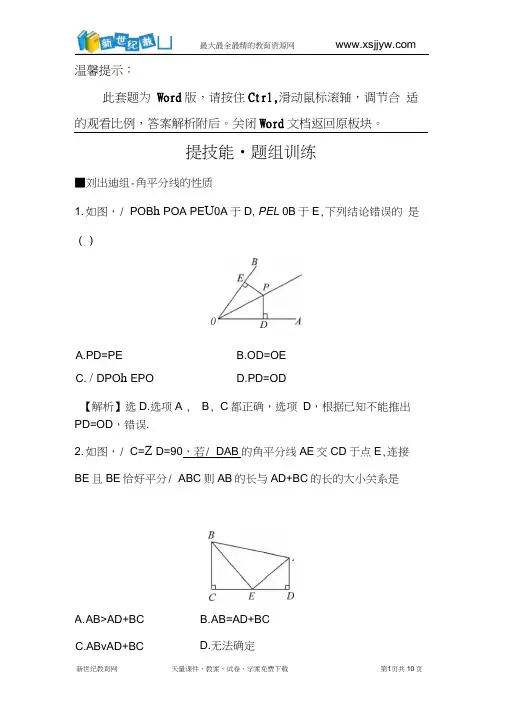
提技能•题组训练■刘出迪组-角平分线的性质1. 如图，/ POB h POA PE U 0A 于D, PEL 0B 于E ,下列结论错误的 是（）PD=OD ，错误.2. 如图，/ C=Z D=90，若/ DAB 的角平分线AE 交CD 于点E ,连接 BE 且BE 恰好平分/ ABC 则AB 的长与AD+BC 的长的大小关系是A.PD=PEB.OD=OEC. / DPO h EPOD.PD=OD B , C 都正确，选项 D ，根据已知不能推出A. A B>AD+BCB. A B=AD+BC 0【解析】选D.选项A ,肓 最大最全最精的教育资源网 90° , EC 二EF 二ED , AzBCE 幻启尸丘,△AEF 幻A ED ,/BC=BF , AF=AD ,「AB 二AF+BF 二AD+BC.【解析】选A.过点E 作EF 山D ,••DE 平分ZADC ，且E 是BC 的中点, /CE=EB=EF ,又/B=90 °，且AE=AE ,•••△BE 坐A FE ,A /AB 二 /EAF.又 T £ED=35 ° , C=90 ° ,•••/DE=90 °-35 °55。

，即/DA=110 ° , DAB=70• EAB=35 °3. 如图，在△ ABC 中, / B=90°, BC=4 /仁/2,则点C 到AE 的距 离是 ________.z?••BE , AE 分别为/ABC 和ZDAB 的角平分线，/ C= zD=【变式训练】 在数学活动课上，小明提出这样一个问题：如图,B=/ C=90 , ADC,CED=35 , )A.35B.45C.55D.65 【解析】选B.过点E 作EF 1AB 于F ,E 是BC 的中点，DE 平 则/ EAB 的度数是肓最大最全最精的教育资源网【解析】vl= d, :AC是ZEAB的平分线，vB=90 °,BC=4，二点C到直线AE的距离为4.答案：4【易错提醒】角平分线上的点到角两边的距离相等，指的是到两边的垂线段的长度相等，所以点C到AE的距离等于BC的长度.www.2i-cn-j 4. 如图，BD平分/ ABC DE垂直于AB于点E,三角形ABC的面积等于90, AB=18 BC=12求DE的长.2i •世纪*教育网【解题指南】根据角平分线上的点到角的两边的距离相等的性质可得点D到BC的距离等于DE,然后根据厶ABC的面积二A ABD的面积+△BCD的面积，列式进行计算即可得解.2-1-c-n-j-y【解析】・.BD平分SBC , DE垂直于AB于点E,•••点D到BC的距离等于DE的长度,V AB=18 , BC=12 ,ill•，S △KBC =S △KBD +S ABCD=〒 X18 DE+] X12 DE=亍DE(18+12)=15 DE△ABC 的面积等于90, 2i*cnj y*com••15 DE=90，解得DE=6.【易错提醒】运用角平分线的性质的注意事项(1) 距离指的是点到角的两边垂线段的长.(2) 性质可以独立作为证明两条线段相等的依据，不需要再证三角形全等.(3) 使用该性质的前提条件是图中有角平分线、有垂直■帝出酣二角平分线的判定1. 如图所示，0B与0C分别是△ ABC的/ ABC和/ACB的平分线，那么/ BAC与/ CAO勺大小关系为()21世纪教育网版权所有A. / BAC2 CACB. / BAC h CACC. / BAC h CACD. 不确定【解析】选B. --CB与CC分别是△ABC的ZABC和ZACB的平分线,•••点C 到AB , BC , AC 的距离相等，21*cnjy*com•••点C也在ZBAC的平分线上，二ZBAC二h CAC.2. 如图，三条公路把A, B, C三个村庄连成一个三角形区域，某地区决定在这个三角形区域内修建一个集贸市场，要使集贸市场到( )21教育名师原创作品三条公路的距离相等，则这个集贸市场应建在A. 在AC BC两边高线的交点处B. 在AC BC两边中线的交点处C. 在/ A,/ B两内角平分线的交点处D. 在AC BC两边垂直平分线的交点处【解析】选C.到三角形两条边的距离相等的点在这两边的夹角的平分线上，所以到三角形三条边的距离都相等的点是这个三角形的三条角平分线的交点.集贸市场应建在/ A, ZB两内角平分线的交点处.【来源:21 •世纪•教育•网】【变式训练】某地为了发展旅游业，要在三条公路上修建一个度假村，使度假村到三条公路的距离相等，这个度假村的选址地点共有（）【来源：21cnj*y.co*m ］A.1处B.2 处C.3处D.4 处形的内心，只有1个，在外部时，为外角平分线的交点，共有3个, 所以，这个度假村的选址地点共有P l, P2 , P3, P44处. 【版权所有：21教育］【方法技巧］有关到线段距离相等的点的位置确定方法1.当点指定在三角形内部时，只要作出内角的平分线的交点即可。

前言：
该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的同步训练习题助力考生查漏补缺，在原有基础上更进一步。

（最新精品同步训练习题）
角的平分线的性质
[学生用书P 37]
1．[2016·淮安]如图12-3-6，在Rt△ABC 中，∠C ＝90°，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12
MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若CD ＝4，AB ＝15，则△ABD 的面积是( )
图12-3-6
A ．15
B ．30
C ．45
D ．60
2．如图12-3-7，在△ABC 中，∠C ＝90°，AC ＝BC ，AD 平分∠BAC 交BC 于D ，DE ⊥AB 于E ，若△BDE 的周长是5 cm ，则AB 的长为__ __．
图12-3-7
3．[2016·咸宁]证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程．下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．
图12-3-8
已知：如图12-3-8，∠AOC＝∠BOC，点P在OC上．
____
求证：___．
请你补全已知和求证，并写出证明过程．
4．如图12-3-9，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，若AB＝10，CD＝3.
图12-3-9
(1)求DE的长；
(2)求△ADB的面积．。

人教版八年级数学12.3 角平分线的性质同步训练一、选择题（本大题共10道小题）1. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D.若PD＝2，则点P到边OA的距离是()A. 1B. 2C. 3D. 42. 下面是黑板上给出的尺规作图题，需要回答横线上符号代表的内容．已知∠AOB.求作：∠AOB的平分线．作法如下：①以点O为圆心，适当长为半径画弧，交OA于点M，交__○__于点N；②分别以点__⊕__为圆心，大于__△__的长为半径画弧，两弧在__⊗__的内部交于点C；③画射线OC，OC即为所求．则下列回答正确的是()A．○表示OA B．⊕表示M，CC．△表示MN D．⊗表示∠AOB3. 如图，在直角坐标系中，AD是Rt△OAB的角平分线，点D的坐标是(0，-3)，那么点D到AB的距离是()A.3B.-3C.2D.-24. 如图,利用尺规作∠AOB的平分线OC,其作法如下:(1)以点O为圆心,适当长为半径画弧,与OA,OB分别交于点D,E;(2)分别以点D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB的内部交于点C;(3)画射线OC,则射线OC就是∠AOB的平分线.这样作图的原理是三角形全等的一种判定方法,这种判定方法是()A.SSSB.SASC.ASAD.AAS5. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D.若CD＝4，AB＝16，则△ABD的面积是()A．14 B．32 C．42 D．566. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为60和35，则△EDF的面积为()A．25 B．5.5 C．7.5 D．12.57. 如图,AD是△ABC的角平分线,DE⊥AB,AB=6 cm,DE=4 cm,S△ABC=30 cm2,则AC 的长为()A.10 cmB.9 cmC.4.5 cmD.3 cm8. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为51和38,则△EDF的面积为 ()A.6.5B.5.5C.8D.139. 如图，平面上到两两相交的三条直线a，b，c的距离相等的点一共有()A．4个B．3个C．2个D．1个10. 如图，点G在AB的延长线上，∠GBC，∠BAC的平分线相交于点F，BE⊥CF 于点H.若∠AFB＝40°，则∠BCF的度数为()A．40°B．50°C．55°D．60°二、填空题（本大题共7道小题）11. 如图,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6 cm,则点P到AB的距离为.12. 如图，OP为∠AOB的平分线，PC⊥OB于点C，且PC＝3，点P到OA的距离为________．13. 如图，已知DB⊥AE于点B，DC⊥AF于点C，且DB＝DC，∠BAC＝40°，∠ADG＝130°，则∠DGF＝________°.14. 如图，已知∠C＝90°，AD平分∠BAC交BC于点D，BD＝2CD，DE⊥AB于点E.若DE＝5 cm，则BC＝________cm.15. 如图，请用符号语言表示“角的平分线上的点到角的两边的距离相等”．条件：____________________________________.结论：PC＝PD.16. 如图,在△ABC中,E为AC的中点,AD平分∠BAC交BC于点D,AB︰AC=2︰3,AD与BE相交于点O.若△OAE的面积比△BOD的面积大1,则△ABC的面积是.17. 如图，△ABC的两条外角平分线BP，CP相交于点P，PE⊥AC交AC的延长线于点E.若△ABC的周长为11，PE=2，S△BPC =2，则S△ABC=.三、解答题（本大题共4道小题）18. 如图，在△ABC中，AD平分∠BAC交BC于点D，DE⊥AB于点E，DF⊥AC 于点F，△ABC的面积是142.5 cm2，AB＝20 cm，AC＝18 cm，求DE的长．19. 已知:如图12-3-12,∠AOC=∠BOC,点P在OC上,.求证:.请你补全已知和求证,并写出证明过程.20. 如图，在△ABC中，∠B＝90°，两直角边AB＝7，BC＝24，斜边AC＝25，P是角平分线AP，CP的交点，PE⊥AB，PF⊥BC，PD⊥AC，垂足分别为E，F，D，求PD的长．21. 如图，P是∠AOB内部的一点，PE⊥OA，PF⊥OB，垂足分别为E，F，且PE＝PF.Q是射线OP上的任意一点，QM⊥OA，QN⊥OB，垂足分别为M，N，则QM与QN相等吗？请证明你的结论．人教版八年级数学12.3 角平分线的性质同步训练-答案一、选择题（本大题共10道小题）1. 【答案】B【解析】如解图，过点P作PG⊥OA于点G，根据角平分线上的点到角的两边距离相等可得，PG＝PD＝2.2. 【答案】D3. 【答案】A[解析] 如图，过点D作DE⊥AB于点E.∵点D的坐标是(0，-3)，∴OD=3.∵AD是△OAB的角平分线，∴ED=OD=3，即点D到AB的距离是3.4. 【答案】 A5. 【答案】B[解析] 如图，过点D作DH⊥AB于点H.由作法得AP平分∠BAC.∵DC⊥AC，DH⊥AB，∴DH＝DC＝4.∴S△ABD＝12×16×4＝32.6. 【答案】D [解析] 如图，过点D 作DH ⊥AC 于点H.又∵AD 是△ABC 的角平分线，DF ⊥AB ， ∴DF ＝DH.在Rt △ADF 和Rt △ADH 中，⎩⎨⎧AD ＝AD ，DF ＝DH ，∴Rt △ADF ≌Rt △ADH(HL)． ∴S Rt △ADF ＝S Rt △ADH .在Rt △DEF 和Rt △DGH 中，⎩⎨⎧DE ＝DG ，DF ＝DH ，∴Rt △DEF ≌Rt △DGH(HL)． ∴S Rt △DEF ＝S Rt △DGH .∵△ADG 和△AED 的面积分别为60和35， ∴35＋S Rt △DEF ＝60－S Rt △DGH .∴S Rt △DEF ＝12.5.7. 【答案】B[解析] 如图,过点D 作DF ⊥AC 于点F .∵AD 是△ABC 的角平分线,DE ⊥AB , ∴DE=DF=4. ∵AB=6,∴S △ABC =S △ABD +S △ACD =×6×4+AC ×4=30, 解得AC=9(cm).故选B .8. 【答案】A[解析] 如图,过点D 作DH ⊥AC 于点H.∵AD 是△ABC 的角平分线,DF ⊥AB ,DH ⊥AC ,∴DF=DH.在Rt △DFE 和Rt △DHG 中,∴Rt△DFE≌Rt△DHG.在Rt△ADF和Rt△ADH中,∴Rt△ADF≌△ADH.设△EDF的面积为x.由题意得,38+x=51-x,解得x=6.5,∴△EDF的面积为6.5.9. 【答案】A[解析] 如图，到三条直线a，b，c的距离相等的点一共有4个．10. 【答案】B[解析] 如图，过点F分别作FZ⊥AE于点Z，FY⊥CB于点Y，FW⊥AB于点W.∵AF平分∠BAC，FZ⊥AE，FW⊥AB，∴FZ＝FW.同理FW＝FY.∴FZ＝FY.又∵FZ⊥AE，FY⊥CB，∴∠FCZ＝∠FCY.由∠AFB＝40°，易得∠ACB＝80°.∴∠ZCY＝100°.∴∠BCF＝50°.二、填空题（本大题共7道小题） 11. 【答案】6 cm [解析] 如图,过点P 作PN ⊥BC 于点N ,PQ ⊥AB 交AB 的延长线于点Q.∵BP ,CP 是两条外角的平分线,PM ⊥AC ,∴PN=PM ,PQ=PN.∴PQ=PM.∵PM=6 cm,∴PQ=6 cm,即点P 到AB 的距离为6 cm .12. 【答案】3【解析】如解图，过点P 作PD ⊥OA 于点D ，∵OP 为∠AOB 的平分线，PC ⊥OB 于点C ，∴PD ＝PC ，∵PC ＝3，∴PD ＝3，即点P 到点OA 的距离为3.13. 【答案】150[解析] ∵DB ⊥AE 于点B ，DC ⊥AF 于点C ，且DB ＝DC ，∴AD 是∠BAC 的平分线．∵∠BAC ＝40°，∴∠CAD ＝12∠BAC ＝20°. ∴∠DGF ＝∠CAD ＋∠ADG ＝20°＋130°＝150°.14. 【答案】15[解析] ∵AD 平分∠BAC ，∠C ＝90°，DE ⊥AB ，∴DC ＝DE ＝5cm.∴BD ＝2CD ＝10 cm ，则BC ＝CD ＋BD ＝15 cm.15. 【答案】∠AOP ＝∠BOP ，PC ⊥OA 于点C ，PD ⊥OB 于点D16. 【答案】10[解析] 如图,过点D 作DM ⊥AC 于点M ,DN ⊥AB 于点N.∵AD 平分∠BAC ,DM ⊥AC ,DN ⊥AB , ∴DM=DN.∵S △ABD ︰S △ADC =BD ︰DC ,且S △ABD =·AB ·DN ,S △ADC =·AC ·DM ,∴BD ∶DC=AB ∶AC=2∶3. 设△ABC 的面积为S ,则S △ADC =S.∵E 为AC 的中点,∴S△BEC=S.∵△OAE的面积比△BOD的面积大1,∴△ADC的面积比△BEC的面积大1.∴S-S=1.∴S=10.故答案为10.17. 【答案】7[解析] 过点P作PF⊥BC于点F，PG⊥AB于点G，连接AP.∵△ABC的两条外角平分线BP，CP相交于点P，∴PF=PG=PE=2.∵S△BPC=2，∴BC·2=2，解得BC=2.∵△ABC的周长为11，∴AC+AB=11-2=9.∴S△ABC =S△ACP+S△ABP-S△BPC=AC·PE+AB·PG-S△BPC=×9×2-2=7.三、解答题（本大题共4道小题）18. 【答案】解：∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，∴DE＝DF.设DE＝x cm，则S△ABD＝12AB·DE＝12×20x＝10x(cm2)，S△ACD＝12AC·DF＝12×18x＝9x(cm2)．∵S△ABC＝S△ABD＋S△ACD，∴10x＋9x＝142.5，解得x＝7.5，∴DE＝7.5 cm.19. 【答案】解:PD⊥OA,PE⊥OB,垂足分别为D,EPD=PE证明:∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°.在△PDO和△PEO中,∴△PDO≌△PEO(AAS).∴PD=PE.20. 【答案】解：连接BP.∵P是角平分线AP，CP的交点，PE⊥AB，PF⊥BC，PD⊥AC，∴PE ＝PD ＝PF.设PE ＝PD ＝PF ＝x.∵S △ABC ＝12AB·BC ＝84，S △ABC ＝12AB·x ＋12AC·x ＋12BC·x ＝12(AB ＋AC ＋BC)·x ＝12×56x ＝28x ， ∴28x ＝84，解得x ＝3.故PD 的长为3.21. 【答案】解：QM ＝QN.证明：∵PE ⊥OA ，PF ⊥OB ，PE ＝PF ，∴OP 是∠AOB 的平分线．又∵Q 是射线OP 上的任意一点，QM ⊥OA ，QN ⊥OB ，∴QM ＝QN.。

12.3角的平分线的性质一、选择题（本大题共10小题，在每小题列出的选项中，选出符合题目的一项）1.如图，点P到AE，AD，BC的距离相等，则下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P是∠BAC，∠CBE，∠BCD的平分线的交点．其中正确的是( )A. ①②③④B. ①②③C. ④D. ②③2.如图，已知点P到AE，AD，BC的距离相等，下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P在∠BAC，∠CBE，∠BCD的平分线的交点上．其中正确的是( )A. ④B. ②③C. ①②③D.①②③④3.到三角形的三边距离相等的点是( )A. 三角形三条高的交点B. 三角形三条内角平分线的交点C. 三角形三条中线的交点D. 无法确定4.如图所示，∠B=∠C=90∘，M是BC的中点，DM平分∠ADC，且∠ADC =110∘，则∠MAB= ( )A. 30∘B. 35∘C. 45∘D. 60∘5.三角形内部到三边距离相等的点是( )A. 三边中线的交点B. 三边垂直平分线的交点C. 三内角平分线的交点D. 三边上高的交点6.如图，AB//CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直.若AD=8，则点P到BC的距离是( )A. 8B. 6C. 4D. 27.在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是．( )A. 点CB. 点DC. 点ED. 点F8.在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是( )A. 点MB. 点NC. 点PD. 点Q9.如图，在△ABC中，∠B=90°，AB=6，BC=8，AD为∠BAC的角平分线，则三角形ADC的面积为( )A. 3B. 10C. 12D. 1510.如图，△ABC的外角平分线BD，CE相交于点P.若点P到AC的距离为3，则点P到AB的距离为( )A. 1B. 2C. 3D. 4二、填空题（本大题共4小）11.如图，点O在△ABC内，且到三边的距离相等.若∠A=60∘，则∠BOC=°．12.如图，点P到∠AOB两边的距离相等，若∠POB=30°，则∠AOB=________．13.如图，在△ABC中，∠C=90∘，AD平分∠BAC与BC边交于点D，BD=2CD，若点D到AB的距离等于5cm，则BC的长为cm．14.如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，MN的长为半径画弧，两弧交于点P，作射线AP交BC于点D，大于12若CD=3，AB=10，则△ABD的面积是________．三、解答题（本大题共3小题，解答应写出文字说明，证明过程或演算步骤）15.如图，∠1=∠2，∠3=∠4.求证：AP平分∠BAC．16.已知：如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.求证：AM平分∠DAB．17.如图，点B，C分别在∠A的两边上，点D是∠A内一点，DE⊥AB，DF⊥AC，垂足分别为E，F，且AB=AC，DE=DF.求证：BD=CD．参考答案1.【答案】A2.【答案】D3.【答案】B4.【答案】B5.【答案】C6.【答案】C7.【答案】C8.【答案】A9.【答案】D10.【答案】C11.【答案】12012.【答案】60°13.【答案】1514.【答案】1515.【答案】证明：过P作PQ⊥AB于Q，PN⊥BC于N，PM⊥AC于M，∵∠1=∠2.∠3=∠4，∴PQ=PN，PN=PM，∴PQ=PM，∵PQ⊥AB，PM⊥AC，∴AP平分∠BAC．16.【答案】证明：过点M作ME⊥AD，垂足为E，∵∠B=∠C=90°，∴MC⊥CD，MB⊥AB，∵DM平分∠ADC，∴∠CDM=∠EDM，又∵MC⊥CD，ME⊥AD，∴ME=MC，又∵MC=MB，∴ME=MB，又∵MB⊥AB，ME⊥AD，∴AM平分∠DAB．17.【答案】证明：连接AD，∵DE⊥AB，DF⊥AC，DE=DF，∴∠BAD=∠CAD，在△ABD和△ACD中AB=AC∠BAD=∠CAD，AD=AD∴△ABD≌△ACD，(SAS)，∴BD=CD．。

前言：该同步练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

以高质量的同步练习题助力考生查漏补缺，在原有基础上更进一步。

（最新精品同步练习题）12.3角的平分线的性质基础巩固1.(题型一)如图12-3-1，在∆ABC中，∠C=90°，AD平分∠BAC，过点D作DE⊥AB于点E，测得BC=9，BE=3，则∆BDE的周长是( )A.15B.12C.9D.6图12-3-1 图12-3-22.(题型一)如图12-3-2，OP平分∠MON，PE⊥OM于点E，PF⊥ON于点F，OA=OB，则图中有对全等三角形．3.(题型一)在∆ABC中，∠BAC和∠ABC的平分线相交于点P，若点P到AB 的距离为10，则点P到边AC和BC的距离和为．4.(题型二)如图12-3-3，P是OC上一点，PD⊥OA于点D，PE⊥OB于点E，F，G分别是OA，OB上的点，且PF=PG，DF=EG．求证：OC是∠AOB的平分线．图12-3-35.(题型二)如图12-3-4，BE=CF，BF⊥AC于点F，CE⊥AB于点E，BF和CE相交于点D．求证：AD平分∠BAC．图12-3-46.(题型一)如图12-3-5,在△ABC中，AD为角平分线，DE⊥AB于点E，DF⊥AC 于点F，AB=10 cm，AC=8 cm，△ABC的面积是45 cm2，求DE的长．图12-3-57.(题型一)如图12-3-6，OC是∠AOB的平分线，P是OC上一点，PD⊥OA交OA于点D，PE⊥OB交OB于点E，F是OC上的另一点，连接DF，EF．求证：DF=EF．图12-3-68.(题型一)如图12-3-7，在四边形ABCD中，AC为∠BAD的平分线，AB=AD，E，F两点分别在AB，AD上，且AE=DF．证明：四边形AECF的面积为四边形ABCD 的面积的一半.图12-3-7能力提升9.(题型二)如图12-3-8，在四边形ABCD中，AB=CD，BA的延长线和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P( )图12-3-8A.有且只有1个B.有且只有2个。

12.3角的平分线的性质基础闯关全练拓展训练1.如图,△ABC的三边AB、BC、AC的长分别为12,18,24,O是△ABC三条角平分线的交点,则S△OAB∶S△OBC∶S△OAC=( )A.1∶1∶1B.1∶2∶3C.2∶3∶4D.3∶4∶52.如图,PM⊥OA,PN⊥OB,垂足分别为点M,N,PM=PN,∠BOC=30°,则∠AOB= .3.如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E.若BC=5 cm,DC=4 cm,则△DEB的周长为cm.4.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD∶DC=3∶2,则D到边AB的距离是.能力提升全练拓展训练1.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为( )A.3B.5C.6D.不能确定2.如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF= .3.如图,已知∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,求∠EAB的度数.三年模拟全练拓展训练1.(2018江苏无锡宜兴期中,16,★★☆)如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO 的面积为20,则△ACO的面积为.2.(2018河北邯郸期末,19,★★☆)如图所示,已知△ABC的周长是20,BO、CO分别平分∠ABC和∠ACB,OD⊥BC 于D,且OD=3,则△ABC的面积是.3.(2018吉林延边安图期末,21,★★☆)如图,AB=AC,BD=CD,DE⊥AB,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.(7分)五年中考全练拓展训练1.如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )A.10B.7C.5D.42.如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD 相交于点D,连接AD,下列结论中不正确的是( )A.∠BAC=70°B.∠DOC=90°C.∠BDC=35°D.∠DAC=55°3.(在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是.核心素养全练拓展训练1.如图,在四边形ABCD中,∠A=90°,AD=8,对角线BD⊥CD,P是BC边上一动点,连接DP.若∠ADB=∠C,则DP 长的最小值为.2.三条公路l1,l2,l3两两相交于A,B,C三点,现计划修建一个商品超市,要求这个超市到三条公路的距离相等,问可供选择的地方有多少处?请画出图形并在图中找出来.12.3 角的平分线的性质基础闯关全练拓展训练1.C ∵O是△ABC三条角平分线的交点,AB、BC、AC的长分别为12,18,24,∴S△OAB∶S△OBC∶S△OAC=AB∶CB∶AC=12∶18∶24=2∶3∶4.故选C.2.答案60°解析∵PM⊥OA,PN⊥OB,PM=PN,∴∠AOC=∠BOC=30°,∴∠AOB=60°.3.答案 5解析∵CD平分∠ACB,DE⊥BC,∠A=90°,∴DE=DA.在Rt△CDE和Rt△CDA中,∴Rt△CDE≌Rt△CDA,∴CE=CA,∴△DEB的周长=BE+BD+DE=BE+BD+DA=BE+BA=BE+AC=BE+CE=BC=5 cm.4.答案 6解析∵BC=15,BD∶DC=3∶2,∴CD=6.∵∠C=90°,AD平分∠BAC,∴D到边AB的距离=CD=6.能力提升全练拓展训练1.C 如图,作PF⊥AD于F,PG⊥BC于G,∵AP是∠BAD的平分线,PF⊥AD,PE⊥AB,∴PF=PE=3,∵BP是∠ABC的平分线,PE⊥AB,PG⊥BC,∴PG=PE=3,∴两平行线AD与BC间的距离为PF+PG=6.2.答案150°解析∵DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∴AD平分∠BAC,∵∠BAC=40°,∴∠CAD=∠BAC=20°,∴∠DGF=∠CAD+∠ADG=20°+130°=150°.3.解析如图,过点E作EF⊥AD交AD于F,∵DE平分∠ADC,EC⊥DC,EF⊥DA,且E是BC的中点,∴CE=EB=EF,又∵∠B=∠AFE=90°,∴AE平分∠DAB,∴∠EAB=∠EAF.又∵∠CED=35°,∠C=90°,∴∠CDE=90°-35°=55°,∴∠CDA=110°,∵∠B=∠C=90°,∴DC∥AB,∴∠CDA+∠DAB=180°,∴∠DAB=70°,∴∠EAB=35°.三年模拟全练拓展训练1.答案16解析∵点O是△ABC三条角平分线的交点,∴点O到AB,AC的距离相等,∴△AOB与△AOC面积的比=AB∶AC=10∶8=5∶4.∵△ABO的面积为20,∴△ACO的面积为16.2.答案30解析如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,∵BO、CO分别平分∠ABC和∠ACB,∴OE=OD,OF=OD,∴OE=OF=OD=3,∵△ABC的周长是20,OD⊥BC于D,且OD=3,∴S△ABC=×AB·OE+×BC·OD+×AC·OF=×(AB+BC+AC)×3=×20×3=30.3.证明在△ABD和△ACD中,∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD,∵DE⊥AB,DF⊥AC,∴DE=DF.五年中考全练拓展训练1.C 作EF⊥BC于F,∵BE平分∠ABC,ED⊥BA,EF⊥BC,∴EF=DE=2,∴S△BCE=BC·EF=×5×2=5,故选C.2.B ∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°-∠ABC-∠ACB=180°-50°-60°=70°,故A选项正确;∵BD平分∠ABC,∴∠ABO=∠ABC=×50°=25°,在△ABO中,∠AOB=180°-∠BAO-∠ABO=180°-70°-25°=85°,∴∠DOC=∠AOB=85°,故B选项错误;∵CD平分∠ACE,∴∠ACD=×(180°-60°)=60°,∴∠BDC=180°-85°-60°=35°,故C选项正确;由BD、CD分别是∠ABC和∠ACE的平分线易证AD是△ABC的外角平分线,∴∠DAC=×(180°-70°)=55°,故D选项正确.3.答案4∶3解析如图,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E、F,由角平分线的性质可得DE=DF,∵S△ABD=AB·DE,S△ACD=AC·DF,∴===,即S△ABD∶S△ACD=4∶3.核心素养全练拓展训练1.答案8解析根据垂线段最短知,当DP⊥BC时,DP的长度最小.∵BD⊥CD,即∠BDC=90°,又∠A=90°,∴∠A=∠BDC,又∠ADB=∠C,∴∠ABD=∠CBD,又DA⊥BA,∴当DP⊥BC时,AD=DP,又AD=8,∴DP长的最小值为8.2.解析先将实际问题转化为数学模型,要求超市到三条公路的距离相等,先观察△ABC的内部,实际上就是在△ABC内找一个点,使它到△ABC的三边的距离相等,这个点应该是△ABC的三条(或两条)角平分线的交点,但除此以外,还应考虑是否还有其他的点也符合要求,因为三条公路都是用直线来表示的,且三角形的互为同旁内角的两个外角的平分线的交点满足到三角形三边所在直线的距离相等,所以在△ABC的外部也存在满足题意的点.如图,(1)作出△ABC的两个内角的平分线,取其交点为O1;(2)作出△ABC所有外角(6个外角)的平分线,取其交点分别为O2,O3,O4,故满足条件的修建点有4处,即O1,O2,O3,O4处.。

12．3角的平分线的性质第1课时角的平分线的性质1．用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC＝∠BOC的依据是( )A．SSS B．ASAC．AAS D．角的平分线上的点到角两边的距离相等2．已知△ABC，用尺规作图作出∠ABC的平分线(保留作图痕迹，但不写作法)．3．如图，OP为∠AOB的平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，则下列结论错误的是( )A．PC＝PD B．∠CPD＝∠DOP C．∠CPO＝∠DPO D．OC＝OD第3题图第4题图4．如图，在△ABC中，∠A＝90°，BD是角平分线，DE⊥BC，垂足是E，AC＝10 cm，CD＝6 cm，则DE的长为( )A．10 cm B．6 cm C．4 cm D．2 cm5．如图，已知点O在∠BAC的平分线上，BO⊥AC，CO⊥AB，垂足分别为D，E，求证：OB＝OC.6．命题“全等三角形对应边上的高线相等”的已知是，结论是．7．证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．已知：如图，∠AOC＝∠BOC，点P在OC上，．求证：．请你补全已知和求证，并写出证明过程．8．在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是( ) A．M点B．N点C．P点D．Q点第8题图第9题图9．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，则点P到BC的距离是( )A．8 B．6C．4 D．210．如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交边AC，AB于点M，N，再分别以M，N为圆心，大于12MN长为半径画弧，两弧交于点P，作射线AP交边BC于点D.若CD＝4，AB＝15，则△ABD的面积为( ) A．15 B．30 C．45 D．60第10题图第11题图11．如图，△ABC的角平分线AD交BC于点D，BD∶DC＝2∶1.若AC＝3 cm，则AB＝．12．如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，且AB＝10 cm，求△DEB的周长．13．证明：全等三角形对应边上的中线相等．如图，已知△ABC≌△A′B′C′，AD，A′D′分别是BC，B′C′边上的中线．求证：AD＝A′D′.14．感知：如图1，AD平分∠BAC，∠B＋∠C＝180°，∠B＝90°.易证：DB＝DC.探究：如图2，AD平分∠BAC，∠ABD＋∠ACD＝180°，∠ABD<90°.求证：DB＝DC.第2课时角的平分线的判定1．如图，OC是∠AOB内部的一条射线，P是射线OC上任意点，PD⊥OA，PE⊥OB.下列条件中：①∠AOC＝∠BOC；②PD＝PE；③OD＝OE；④∠DPO＝∠EPO.能判定OC是∠AOB 的平分线的有( )A．1个B．2个C．3个D．4个第1题图第2题图2．如图，∠AOB＝70°，QC⊥OA于点C，QD⊥OB于点D，若QC＝QD，则∠AOQ＝．3．如图，BE＝CF，DE⊥AB的延长线于点E，DF⊥AC于点F，且DB＝DC，求证：AD 是∠BAC的平分线．4．到△ABC的三条边距离相等的点是△ABC的( )A．三条中线的交点B．三条角平分线的交点C．三条高的交点D．以上均不对5．如图，△ABC的三边AB，BC，CA的长分别为40，50，60，其三条角平分线交于点O，则S△ABO∶S△BCO∶S△CAO＝．6．如图，铁路OA和铁路OB交于点O处，河道AB与铁路分别交于A处和B处，试在河岸上建一座水厂M，要求M到铁路OA，OB的距离相等，则该水厂M应建在图中什么位置？请在图中标出M点的位置．7．D，E分别是△ABC中边AB，AC上的一点，在△ABC内有一点O，使OE＝OD，则AO平分∠CAB吗？解：AO平分∠CAB.理由如下：∵点O到∠CAB两边的距离相等，∴点O在∠CAB的平分线上．∴AO平分∠CAB.以上解法是否正确？若不正确，请说明理由，并写出正确的结论．8．如图，AD⊥OB，BC⊥OA，垂足分别为D，C，AD与BC相交于点P，若PA＝PB，则∠1与∠2的大小关系是( )A．∠1＝∠2 B．∠1＞∠2C．∠1＜∠2 D．无法确定9．如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB ＝( )A．30° B．35° C．45° D．60°第9题图第10题图10．如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3，则△ABC的面积是．11．三条公路两两相交于A，B，C三点，现计划修建一个商品超市，要求这个超市到三条公路距离相等，则可供选择的地方有处．12．如图，∠ABC的平分线与∠ACB的外角平分线相交于点D，连接AD.求证：AD是∠BAC 的外角平分线．13．如图，在△ABC中，∠B＝∠C，D是BC边上一动点，过点D作DE⊥AB，DF⊥AC，E，F分别为垂足，则当点D移动到什么位置时，AD恰好平分∠BAC？请说明理由．14．如图，在四边形ABDC中，∠D＝∠B＝90°，O为BD的中点，且AO平分∠BAC.求证：(1)CO平分∠ACD；(2)OA⊥OC；(3)AB＋CD＝AC.参考答案：12．3 角的平分线的性质 第1课时 角的平分线的性质1．A2．解：作图略． 3．B 4．C5．证明：∵点O 在∠BAC 的平分线上，BO ⊥AC ，CO ⊥AB ，∴OE ＝OD ，∠BEO ＝∠CDO ＝90°. 在△BEO 与△CDO 中，⎩⎪⎨⎪⎧∠BEO ＝∠CDO ，OE ＝OD ，∠EOB ＝∠DOC ，∴△BEO ≌△CDO(ASA )． ∴OB ＝OC.6．两个三角形是全等三角形，它们对应边上的高线相等． 7．证明：∵PD ⊥OA ，PE ⊥OB ，∴∠PDO ＝∠PEO ＝90°. 在△PDO 和△PEO 中，⎩⎪⎨⎪⎧∠PDO ＝∠PEO ，∠POD ＝∠POE ，OP ＝OP ，∴△PDO ≌△PEO(AAS )． ∴PD ＝PE. 8．A 9．C 10．B 11．6cm ．12．解：∵AD 平分∠BAC 交BC 于点D ，DE ⊥AB ，∠C ＝90°，∴CD ＝DE.在Rt △ACD 和Rt △AED 中，⎩⎪⎨⎪⎧CD ＝ED ，AD ＝AD ，∴Rt △ACD ≌Rt △AED(HL )．∴AE ＝AC.∴△DEB 的周长为DE ＋DB ＋EB ＝CD ＋DB ＋BE ＝BC ＋BE ＝AC ＋BE ＝AE ＋BE ＝AB ＝10 cm .13．证明：∵△ABC ≌△A′B′C′，∴AB ＝A′B′，∠B ＝∠B′，BC ＝B′C′.又∵AD ，A′D′分别是BC ，B′C′边上的中线，∴BD ＝12BC ，B′D′＝12B′C′.∴BD ＝B′D′.在△ABD 和△A′B′D′中， ⎩⎪⎨⎪⎧AB ＝A′B′，∠B ＝∠B′，BD ＝B′D′，∴△ABD ≌△A′B′D′(SAS )． ∴AD ＝A′D′.14．证明：过点D 分别作DE ⊥AB 于点E ，DF ⊥AC 交AC 的延长线于点F ，∵AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ， ∴DE ＝DF ，∠DEB ＝∠F ＝90°.∵∠B ＋∠ACD ＝180°，∠ACD ＋∠FCD ＝180°， ∴∠B ＝∠FCD.在△DFC 和△DEB 中，⎩⎪⎨⎪⎧∠F ＝∠DEB ，∠FCD ＝∠B ，DF ＝DE ，∴△DFC ≌△DEB(AAS )． ∴DC ＝DB.第2课时 角的平分线的判定1．D2． 35°．3．证明：∵DE ⊥AB ，DF ⊥AC ，∴∠BED ＝∠DFC ＝90°.在Rt △DEB 和Rt △DFC 中，⎩⎪⎨⎪⎧BE ＝CF ，DB ＝DC ，∴Rt △DEB ≌Rt △DFC(HL )．∴DE ＝DF.∴AD 是∠BAC 的平分线． 4．B5．4∶5∶6．6．解：图略．提示：作∠AOB 的平分线，与AB 的交点即为点M 的位置．7．解：不正确．以上解法忽视了OD ，OE 分别垂直于AB ，AC 的条件，故产生错误．正确的结论是“AO 不一定平分∠CAB ”． 8．A 9．B10．31.5． 11．4． 12．证明：过点D 分别作DE ⊥AB ，DG ⊥AC ，DF ⊥BC ，垂足分别为E ，G ，F. 又∵BD 平分∠ABC ，CD 平分∠ACF ， ∴DE ＝DF ，DG ＝DF. ∴DE ＝DG.∴AD 平分∠EAC ，即AD 是∠BAC 的外角平分线．13．解：移动到BC 的中点时，AD 恰好平分∠BAC.理由如下：∵D 是BC 的中点， ∴BD ＝CD.∵DE ⊥AB ，DF ⊥AC ， ∴∠DEB ＝∠DFC ＝90°. 在△DEB 和△DFC 中，⎩⎪⎨⎪⎧∠DEB ＝∠DFC ，∠B ＝∠C ，BD ＝CD ，∴△DEB ≌△DFC(AAS )． ∴DE ＝DF.又∵DE ⊥AB ，DF ⊥AC ， ∴AD 平分∠BAC. 14．证明：(1)过点O 作OE ⊥AC 于点E. ∵∠B ＝90°，AO 平分∠BAC ， ∴OB ＝OE.∵O 为BD 的中点， ∴OB ＝OD. ∴OE ＝OD.又∵∠D ＝90°，∠OEC ＝90°， ∴CO 平分∠ACD.(2)在Rt △ABO 和Rt △AEO 中，⎩⎪⎨⎪⎧AO ＝AO ，OE ＝OB ， ∴Rt △ABO ≌△Rt △AEO(HL )．∴∠AOB ＝∠AOE ＝12∠BOE.同理，∠COD ＝∠COE ＝12∠DOE.∵∠AOC ＝∠AOE ＋∠COE ，∴∠AOC ＝12∠BOE ＋12∠DOE ＝12×180°＝90°.∴OA ⊥OC.(3)∵Rt △ABO ≌Rt △AEO ， ∴AB ＝AE.同理可得CD ＝CE.∵AC ＝AE ＋CE ，∴AB ＋CD ＝AC.。

课后训练基础稳固1．作∠的均分线，合理的次序是 () ．AOBOC①作射线 OC ；②以 O 为圆心，适合长为半径画弧，交OA 于点 D ，交 OB 于点 E ；③分别以点 D ， E 为圆心，大于1DE的长为半径画弧，两弧在∠.2AOB 内交于点 CA ．①②③B ．②①③C ．②③①D ．③②① 2．三角形中到三边距离相等的点是( ) ． A ．三条边的垂直均分线的交点 B ．三条高的交点 C ．三条中线的交点D ．三条内角均分线的交点 3．如图，∠ 1＝∠ 2， PD ⊥ OA ， PE ⊥ OB ，垂足分别为 D ， E ，以下结论错误的选项是 () ．A ． PD ＝ PEB ． OD ＝ OEC ．∠ DPO ＝∠ EPOD ． PD ＝OD4．如图，在△ ABC 中 ，∠ ACB ＝ 90°， BE 均分∠ ABC ，DE ⊥ AB 于点 D ，假如 AC ＝ 3 cm ，那么 AE ＋ DE 等于 ( ) ．A ． 2 cmB ． 3 cmC ． 4 cmD ．5 cm5．在 △ ABC 中，∠ C ＝ 90°，点 O 为△ ABC 三条角均分线的 交点， OD ⊥ BC 于点 D ，OE ⊥AC 于点 E ，OF ⊥ AB 于点 F ，且 AB ＝ 10 cm ， BC ＝ 8 cm ， AC ＝ 6 cm ，则点 O 到三边 AB ， AC ， BC 的距离分别为 ( ) ．A ． 2 cm,2 cm,2 c mB ． 3 cm,3 cm,3 cmC ． 4 cm,4 cm,4 cmD ． 2 cm,3 cm,5 cm能力提高6．以下图，∠AOB ＝ 60°， CD ⊥ OA 于点 D ，CE ⊥ OB 于点 E ，且 CD ＝ CE ，则∠ DCO ＝________.7．在△ ABC 中，∠ C ＝ 90°， AD 均分∠ BAC 交 BC 于点 D ，若 BC ＝ 32，且 BD ∶ CD ＝9∶ 7，则 D 到 AB 的距离为 __________．8．点 O 是△ ABC 内一点，且点 O 到三边的距离相等，∠ A ＝ 60°，则∠ BOC 的度数为 __________．9．如图， BN 是∠ ABC 的均分线，点 P 在 BN 上，点 D ， E 分别在 AB ， BC 上，∠ BDP ＋∠ BEP ＝ 180°，且∠ BDP ，∠ BEP 都不是直角，求证： PD ＝ PE .word10．如图，在△ABC中，∠C＝ 90°，AD均分∠BAC，DE⊥AB于点E，点F在AC上，BD ＝DF.(1)试说明 CF＝EB的原因；( 2) 请你判断AE，AF与 BE的大小关系，并说明原因．11．如图，木匠师傅常用角尺来作随意一个角的均分线，请你设计一个方案，只用角尺来作∠ AOB的均分线，并说明原因．12．已知：以下图，BF与CE订交于点D，BD＝CD，BF⊥AC于点F，CE⊥AB于点E，求证：点 D在∠ BAC的均分线上．word参照答案1． C2．D 点拨：由角的均分线的性质知，到角两边距离相等的点在角的均分线上，因此到三角形三边距离相等的点 是三条内角均分线的交点．3．D 点拨： 由角均分线的性质得 ＝ ，从而可证△≌△，得＝ ，∠PE PDPEOPDOOE OD DPO＝∠ EPO ，但 PD ＝ OD 是错误的．4． B 点拨： 因为 BE 均分∠，∠ ＝ 90°， ⊥于点，ABCACBDEABD因此 DE ＝ EC ， AE ＋ DE ＝ AE ＋ EC ＝ AC ＝ 3 cm.5． A 点拨： 因为点 O 为△ ABC 三条角均分线的交点， OD ⊥ BC 于点 D ， OE ⊥AC 于点E ，OF ⊥ AB 于点 F ，因此设点 O 到三边 AB ， AC ， BC 的距离为 x cm.由三角形的面积公式得，1× 6x ＋ 1 × 8x ＋ 1 × 10x ＝ 1× 6× 8，解得 x ＝ 2(cm) ．2 2 226． 60° 点拨： 因为 CD ⊥OA 于点 D ， CE ⊥ OB 于点 E ，且 CD ＝ CE ， 因此 为∠ 的均分线．OCAOB因此∠ AOC ＝ 30° .因此∠ ＝60°.DCO7． 14 点拨： 设 BD ＝ 9x ，CD ＝ 7x ， 因此 9x ＋ 7x ＝ 32，解得 x ＝ 2.因此 BD ＝ 18， CD ＝ 14. 因为 AD 均分∠ BAC 交 BC 于点D ， 则点 D 到 AB 的距离等于 CD ＝ 14. 8． 120° 点拨： 点 O 到三边的距离相等， 因此点 O 是三个内角的均分线的交点．又因为∠ ＝ 60°，A因此∠ B ＋∠ C ＝120°， 1 ∠ B ＋ 1∠ C ＝ 60° .2 2因此∠ BOC ＝ 180°－ 60°＝ 120° .9．证明：如图，过点 P 分别作 PF ⊥ AB 于点 F ， PG ⊥BC 于点 G ，∵ BN 是∠ ABC 的均分线， ∴ PF ＝PG .又∵∠ BDP ＋∠ BEP ＝ 1 80°，∠ PEG ＋∠ BEP ＝ 180°， ∴∠ BDP ＝∠ PEG .在△ PFD 和△ PGE 中，FDPGEP,∵PFD PGE,PF PG,∴△ PFD ≌△ PGE (AAS) ． ∴ PD ＝PE .10． 解： (1) ∵∠ C ＝ 90°， ∴ DC ⊥AC .∵ AD 均分∠ BAC ， DE ⊥ AB ，∴ DC ＝DE ，∠ DEB ＝∠ C ＝90° . 在 Rt △ DCF 与 Rt △ DEB 中，wordDF DB ,∵DC DE ,∴Rt △DCF≌ Rt△DEB(HL) ．∴CF＝EB.(2)AE＝ AF＋ BE.原因以下：∵ AD均分∠ BAC，∴∠ CAD＝∠ EAD.又∵ AD＝ AD，∠ C＝∠ DEA＝90°，∴△ ACD≌△ AED(AAS)．∴ AC＝AE.由 (1) 知BE＝CF，∴AC＝AF＋ CF＝AF＋ BE.∴AE＝AF＋ BE.11．解：方案：如图，(1) 在射线OA上截取OM为必定的长度a，在 OB上截取 ON＝ a；(2)分别过点 M， N作 OA，OB的垂线，设交点为 P；(3)连结 OP，则 OP就是∠ AOB的均分线．原因：在 Rt △OMP和 Rt △ONP中，OM＝ON，OP＝OP，因此 Rt△OMP≌Rt △ONP(HL) ．因此∠ MOP＝∠ NOP.12．证明：∵BF⊥AC，CE⊥AB，∴∠ BED＝∠ CFD＝90°.在△ BDE和△ CDF中，BED CFD,∵BDE CDF ,BD CD,∴△ BDE≌△ CDF(AAS)．∴DE＝DF.∵BF⊥AC， CE⊥AB，∴∠ BAD＝∠ CAD，即点 D在∠ BAC的均分线上．word。

第十二章12.3角的平分线的性质姓名： ________________________ 班 考号： ________________________ 1. 如图所示，已和一条定长线段在Z/I 防内找一点出使点P 到0A,防的距离都等 于日，作法如下：①在ZAOB 内作防的垂线段NH,使NH 二a, 〃为垂足;②过艸作NM// 0B\③作AAOB 的平分线0P,与翩交于点P;④点戶即为所求.其中③的依据是（）A. 平行线之间的距离处处相等B. 角的内部到角的两边的距离相等的点在角的平分线上C. 角的平分线上的点到角的两边的距离相等D. 线段垂直平分线上的点到线段两端点的距离相等2. 如图，〃平分ZAOB, PCLOA, PD10B,垂足分别为C, D,则下列结论中错误的是（）A. PC=PDB. OD=OCC. 乙 DPO 二乙 CPOD. PC=OC 3. 如图，在中，,他平分ZABC, EDI AB 于点D,若AC=5 cm,则AE+DE 等于 ()A. 3 cmB. 4 cm C ・5 cm D.6 cm 4.如图，在中，ZQ90° , ZJ-30°，勿是SBC 的平分线,〃-20,则％的长是A. 20B. 20C.评卷人得分一、选择题 学校:B5. 如图，的外角上BCD,上CBE 的平分线相交于点穴连接你则下列结论正确的是（）6. 如图所示，在△ /D7中，, AC=BQ AD 是ZD1C 的平分线,％丄也垂足为2若7. 如图，已知AB=AC, AE 二AF, BE 与CF 交于点、D,贝I 」:①'ABE^'ACF;②△跑灼△宓;③〃在 Z 浙C 的平分线上，以上结论中，正确的是（）A.①①② 8. 已知△肋Q 的周长是60cm,三条角平分线交于P 点,且P 点到 氏的距离是10cm,则△肋C 的面积为 （）2 2 A. 600 cmB. 300 cmC.300 cm 2 D.无法确定 9. 如图所示，点P 到AE, AD,力的距离相等，则下列说法:①点P 在ABAC 的平分线上;②点P 在ZQE 的平分线上;③点尸在Z/O 的平分线上;④点户是ABAC. ZCBE t的平分线的交点.其中，正确的是（）A. 4 个B. 3 个C. 2 个D. 1个 10. 如图，在中，AB 二AC,初平分ZBAC, DEX.AB 于E 点、,DFLAC 于F 点、,有下列结论:®BD=DC;②〃③初上任意一点到 也化的距离相等;④初上任意一点到〃点与C点A. AF 平分BC AFLBCB. SF 平分/ACD.以上结论都正确 c.B.② D.①②③C.A B E14 cmD. 10 cm的距离不等.其中正确的是（）11.如图所示，直线日,方,c表示交叉的公路,现要建一货物屮转站，要求它到三条公路的距离相等,则可供选择的站址有________ 处.12._______ 如图，点0是内一点，且到三边的距离相等,Z/I-600，则ZBOC的度数为•13.如图所示，已知BDA.AE于点B, DCA.AF于点C,且DB二DC, ZBAC^O° , ZADG=13O° ,则14.________________________ 如图，在四边形肋C刀中，Z^-90°,初珂连接BD, BDLDC y乙ADB二乙C.若P是〃C边上一动点，则莎长的最小值为.15. ________ 如图，在△血农中，AB=BC,应=16 cm, ZABC=80° ,弘平分ZABC, DE//BC,则AD=,乙EDB _______ .评卷人得分二、填空题B.③④C.D.①②③④评卷人得分解答题A.①②①②③16.如图，在Rt△血农中，,AD平分Z CAB, DEI AB于E若Ag BC之，〃-3,求化'的长.17.二和△PG?的面积相等,求证："平分ZAOC.18.如图，已知〃丄M于点D, BEL AC于点£, CD交BE于点、0.(1)若求证：点0在的平分线上；(2)若点0在Z胡Q的平分线上，求证：00%19.如图所示，PA二PB, ZPA附ZPBN=\80°，求证：莎平分GOB.20.如图，△肋C屮，肋平分ZBAC,必;丄％且平分BC, DEIAB于E, DFIAC于F.求证:駁参考答案1.【答案】B【解析】由要找角内部的点到角两边的距离相等可知本题考查对角的平分线的判定的掌握.2.【答案】D【解析\ JOP平分ZAOB, :. ZAOP=ZPOB.由PC丄％刖丄血可得Z ODP二Z OCP,且OP=OP,・•・ R t △ "0ZZ R t △POC,所以Z DPO二乙CPO, OD二OC, PD二PC.若PC=OQ 乙POB二乙PO&45° ,则OB LOA,由图可知D项错误，故选D.3.【答案】C【解析】根据角的平分线的性质可知DE二CE,所以AE+DE二AE+CE二ACt cm.4.【答案】D【解析】劭是的平分线，所以ZABD=ZCBD=30° ,所以AD二BDQ,又Z 67^-30 ° ,所以0=10.5.【答案】B【解析】过厂点分别作侃BC,所在直线的垂线，垂足分别为G, A；由角平分线的性质可得沏心67=忧再由角平分线的判定定理即可得出平分ABAC.由已知条件推不出结论"F平分比：AFL BC.6.【答案】A【解析】・••肋是乙BAC的平分线，・・・ZG〃二乙EAD，又1评卷人得分O LI四、证明题DE_LAB, ZO90°・ CD二ED,又AD二AD,；・△JCM厶AEDQW), :. AE=AC,又AC二BC, :./XDBE的周长二DE+EB+BD二CD+DB+EB二BC+EB二AC+EB二AE+EB二AB=\ 2 cm.7.【答案】D【解析】由题意可知・・・ZQ=Z〃,・•・△财竺△宓(AAS) ;△/!仞竺劭(SSS),所以ZCAD二ZBAD,所以点〃在Z胡Q的平分线上,所以①②③都正确.8.【答案】B【解析】角平分线上的点到角两边的距离相等，则△/!%的面枳=X60X10-300cm'；9.【答案】A【解析】过点戶分别向AE, AD, BC作垂线段，由角的内部到角的两边的距离相等的点在角的平分线上可证明①②③④都正确.10.【答案】C【解析\・・• AB二AC, AD平分ZBAC, .・・/!〃是％的垂直平分线，:・BD二DC,且上任意一点到AB,AC的距离相等，・・・①③正确，④错误；又•: DEIAB,DFIAC,:・DE二DF,・••②正确. 故选 C.11.【答案】412.【答案】120°13.【答案】150°14.【答案】415.【答案】8 cm;40° 16.【答案】•・•初平分ZCAB,DE丄AB, ZG90° ,:・CD二DE. •: CD冯，：・DE冷. 17.【答案】证明：如图，过点"分别作肱丄如M丄垂足分别为点2点人:・AB・ PE二CD • PF,又J AB二CD, :. PE二PF,又J PEI OB, PFIOD,・•・〃平分ZAOC.18.【答案】•・•点0在Z胡C的平分线上，OE=OD.又'：BEVAC y CD LAB, :. ZOEC=ZODB=90a .在和△沏中,・•・△ OEd△ 妙(ASA),・・・OC=OD.19.【答案】证明：如图，过点戶分别作PELO•札PFJLON,垂足分别为鸟斤则ZPEANPFB3。

12.3角的平分线的性质第1课时角的平分线的性质01课前预习J要点感知1角的平分线的性质：角的平分线上的点到角的两边的距离________ .预习练习1-1如图,OP平分ZAOB,PC丄OA,垂足为C,PD丄OB,垂足为D,则PC与PD的大小关系是（）A.POPDB.PC=PDC.PC<PDD.不能确定要点感知2命题证明的一般步骤为：（1）明确命题中的已知和求证；（2）根据题意画出图形，并用数学符号表示已知和求证；（3）写出证明过程.预习练习2-1命题“全等三角形对应角的角平分线长度相等”的己知是—，求证是—.02半堂训练知识点1角平分线的作法1•用直尺和圆规作一个角的平分线的示意图如图所示，则能说明ZAOC=ZBOC的依据是（）A.SSSB.ASAC.AASD.角平分线上的点到角两边距离相等2.已知AABC,用尺规作图作tilZABC的角平分线,保留作图痕迹，但不写作法.知识点2角平分线的性质3.如图，BD是ZABC的平分线，P是BD±的一点，PE丄BA于点E, PE=4 cm,则点P到边BC的距离为cm.、C4. 如图所示,E 是ZAOB 的平分线上一点,EC 丄OA,ED 丄OB,垂足分别为C, D.求证：OC=OD.5. 如图，BD 平分ZABC, DE 垂直于AB 于E 点，Z\ABC 的面积等于90, AB=18, BC=12,求DE 的长.知识点3命题证明6. 命题“全等三角形对应边上的高线相等”的已知是—，结论是7. 证明：全等三角形对应边上的屮线相等.03课后作业&如图,AD 〃BC,ZABC 的角平分线BP 与ZBAD 的角平分线AP 相交于点P,作PE±AB 于点E.若PE=2, 则两平行线AD 与BC 间的距离为9. 如图，在AABC, ZC=90° , ZCAB=50° ,按以下步骤作图：①以点A 为圆心，小于AC 的长为半径画 弧，分别交AB, AC 于点E 、F ；②分别以点E,F 为圆心，大于］EF 的长为半径画弧，两弧相交于点G ；2③作射线AG 交BC 边于点D,则ZCDA 的度数为 _______ .10. 已知，如图所示，ZXABC 的角平分线AD 将BC 边分成2 ： 1两部分，若AC=3 cm,则AB 二—.a第8题图 第9题图11.己知:如图所示，点0在ZBAC的平分线上,BO丄AC,CO丄AB,垂足分别为D, E,求证：OB=OC.12.如图,AABC 中,ZC=90° ,AC=BC,AD 平分ZBAC 交BC 于D,DE丄AB,垂足为E,且AB=10。

《12.3 角的平分线的性质》一、填空题1．如图，∠B=∠D=90゜，根据角平分线性质填空：（1）若∠1=∠2，则______=______．（2）若∠3=∠4，则______=______．2．如图，BD是∠ABC的平分线，DE⊥AB于E，DF⊥BC于F，AB=12，BC=15，S△ABD =36，则S△BCD=______．3．如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则S△ABO ：S△BCO：S△CAO等于______．4．如图，AD是△ABC的角平分线，若AB=2AC．则S△ABD ：S△ACD=______．二、选择题5．如图，已知点P、D、E分别在OC、OA、OB上，下列推理：①∵OC平分∠AOB，∴PD=PE；②∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD=PE；③∵PD⊥OA，PE⊥OB，∴PD=PE；其中正确的个数有（）A．0个B．1个C．2个D．3个6．如图△ABC中，∠ACB=90゜，AD平分∠BAC交BC于D，DE垂直AB于E，若DE=1.5cm，BD=3cm，则BC=（）A．3cm B．7.5cm C．6cm D．4.5cm7．在△ABC中，∠C=90゜，AD平分∠BAC交BC于D，BD：DC=3：2，点D到AB的距离为6，则BC 长为（）A．10 B．20 C．15 D．258．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD=OE D．不能确定三、解答题9．如图，△ABC中，∠C=90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE=CF，求证：（1）DE=DC；（2）BD=DF．10．如图，四边形ABCD中，AB=AD，CB=CD，点P是AC上一点，PE⊥BC于E，PF⊥CD于F，求证：PE=PF．11．已知，如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM=PN．12．如图，BD是∠ABC的平分线，DE⊥AB于E，S=90，AB=18，BC=12，求DE的长．△ABC13．如图．已知在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR ⊥AB于R，AB=7，BC=8，AC=9．（1）求BP、CQ、AR的长．（2）若BO的延长线交AC于E，CO的延长线交AB于F，若∠A=60゜，求证：OE=OF．《12.3 角的平分线的性质》参考答案与试题解析一、填空题1．如图，∠B=∠D=90゜，根据角平分线性质填空：（1）若∠1=∠2，则BC = DC ．（2）若∠3=∠4，则AB = AD ．【考点】角平分线的性质．【分析】（1）根据角平分线性质推出即可；（2）根据角平分线性质推出即可．【解答】解：（1）∵∠B=∠D=90°，∴AB⊥BC，AD⊥DC，∵∠1=∠2，∴BC=CD，故答案为：BC，DC．（2）∵AB⊥BC，AD⊥DC，∵∠3=∠4，∴AB=AD，故答案为：AB，AD．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边距离相等．2．如图，BD是∠ABC的平分线，DE⊥AB于E，DF⊥BC于F，AB=12，BC=15，S△ABD =36，则S△BCD= 45 ．【考点】角平分线的性质．【分析】首先根据△ABD的面积计算出DE的长，再根据角平分线上的点到角两边的距离相等可得DE=DF，然后计算出DF的长，再利用三角形的面积公式计算出△BCD的面积即可．【解答】解：∵S△ABD=36，∴•AB•ED=36，×12×ED=36，解得：DE=6，∵BD是∠ABC的平分线，DE⊥AB于E，DF⊥BC于F，∴DE=DF，∴DF=6，∵BC=15，∴S△BCD=•CB•DF=×15×6=45，故答案为：45．【点评】此题主要考查了角平分线的性质，关键是掌握角平分线上的点到角两边的距离相等．3．如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则S△ABO ：S△BCO：S△CAO等于2：3：4 ．【考点】角平分线的性质；三角形的面积．【专题】常规题型．【分析】由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB、BC、CA的高相等，利用面积公式即可求解．【解答】解：过点O 作OD ⊥AC 于D ，OE ⊥AB 于E ，OF ⊥BC 于F ，∵O 是三角形三条角平分线的交点，∴OD=OE=OF ，∵AB=20，BC=30，AC=40，∴S △ABO ：S △BCO ：S △CAO =2：3：4．故答案为：2：3：4．【点评】此题主要考查角平分线的性质和三角形面积的求法，难度不大，作辅助线很关键．4．如图，AD 是△ABC 的角平分线，若AB=2AC ．则S △ABD ：S △ACD = 2 ．【考点】角平分线的性质．【分析】过D 作DM ⊥AC 于M ，DN ⊥AB 于N ，根据角平分线性质得出DM=DN ，根据三角形面积公式求出即可．【解答】解：过D 作DM ⊥AC 于M ，DN ⊥AB 于N ，∵AD 是△ABC 的角平分线，∴DM=DN ，∴S △ABD ：S △ACD =（AB ×DN ）：（AC ×DM ）=AB ：AC=2AC ：AC=2，故答案为：2．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．二、选择题5．如图，已知点P、D、E分别在OC、OA、OB上，下列推理：①∵OC平分∠AOB，∴PD=PE；②∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD=PE；③∵PD⊥OA，PE⊥OB，∴PD=PE；其中正确的个数有（）A．0个B．1个C．2个D．3个【考点】角平分线的性质．【分析】直接根据角平分线的性质进行解答即可．【解答】解：∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD=PE．故选B．【点评】本题考查的是角平分线的性质，即角平分线上的点到角两边的距离相等．6．如图△ABC中，∠ACB=90゜，AD平分∠BAC交BC于D，DE垂直AB于E，若DE=1.5cm，BD=3cm，则BC=（）A．3cm B．7.5cm C．6cm D．4.5cm【考点】角平分线的性质．【分析】根据角平分线的性质得出CD长，代入BC=BD+DC求出即可．【解答】解：∵∠ACB=90°，∴AC⊥BC，∵DE⊥AB，AD平分∠BAC，∴DE=DC=1.5cm，∵BD=3cm，∴BC=BD+DC=3cm+1.5cm=4.5cm，故选D．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．7．在△ABC中，∠C=90゜，AD平分∠BAC交BC于D，BD：DC=3：2，点D到AB的距离为6，则BC 长为（）A．10 B．20 C．15 D．25【考点】角平分线的性质．【分析】过点D作DE⊥AB于E，根据角平分线上的点到角的两边的距离相等可得DC=DE，然后求出BD的长，再根据BC=BD+DE代入数据进行计算即可得解．【解答】解：如图，过点D作DE⊥AB于E，∵点D到AB的距离为6，∴DE=6，∵∠C=90°，AD平分∠BAC交BC于D，∴DC=DE=6，∵BD：DC=3：2，∴BD=×3=9，∴BC=BD+DE=9+6=15．故选C．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键，作出图形更形象直观．8．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD=OE D．不能确定【考点】角平分线的性质．【分析】根据三角形的角平分线相交于一点，连接AO，则AO平分∠BAC，然后根据角平分线上的点到角的两边的距离相等解答．【解答】解：如图，连接AO，∵∠B、∠C的角平分线交于点0，∴AO平分∠BAC，∵OD⊥AB，OE⊥AC，∴OD=OE．故选C．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，根据三角形的角平分线相交于一点作辅助线并判断出AO平分∠BAC是解题的关键．三、解答题9．如图，△ABC中，∠C=90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE=CF，求证：（1）DE=DC；（2）BD=DF．【考点】角平分线的性质；全等三角形的判定与性质．【专题】证明题．【分析】（1）根据角平分线上的点到角的两边的距离相等证明即可；（2）利用“边角边”证明△BDE和△FDC全等，再根据全等三角形对应边相等证明即可．【解答】证明：（1）∵∠C=90°，AD是∠BAC的平分线，DE⊥AB，∴DE=DC；（2）在△BDE和△FDC中，，∴△BDE≌△FDC（SAS），∴BD=DF．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，是基础题，熟记性质是解题的关键．10．如图，四边形ABCD中，AB=AD，CB=CD，点P是AC上一点，PE⊥BC于E，PF⊥CD于F，求证：PE=PF．【考点】全等三角形的判定与性质；角平分线的性质．【专题】证明题．【分析】根据“SSS”可得到△ABC≌△ADC，则∠BCA=∠DCA，再利用角平分线的性质即可得到结论．【解答】证明：在△ABC和△ADC中，，∴△ABC≌△ADC（SSS），∴∠BCA=∠DCA，∵PE⊥BC于E，PF⊥CD于F，∴PE=PF．【点评】本题考查了全等三角形的判定与性质：三边都对应相等的两三角形全等；全等三角形的对应边相等，对应角相等．角平分线的性质：角的平分线上的点到角的两边的距离相等．11．已知，如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM=PN．【考点】角平分线的性质；全等三角形的判定与性质．【专题】证明题．【分析】根据角平分线的性质以及已知条件证得△ABD≌△CBD（SAS），然后由全等三角形的对应角相等推知∠ADB=∠CDB；再由垂直的性质和全等三角形的判定定理AAS判定△PMD≌△PND，最后根据全等三角形的对应边相等推知PM=PN．【解答】证明：在△ABD和△CBD中，AB=BC（已知），∠ABD=∠CBD（角平分线的性质），BD=BD（公共边），∴△ABD≌△CBD（SAS），∴∠ADB=∠CDB（全等三角形的对应角相等）；∵PM⊥AD，PN⊥CD，∴∠PMD=∠PND=90°；又∵PD=PD（公共边），∴△PMD≌△PND（AAS），∴PM=PN（全等三角形的对应边相等）．【点评】本题考查了角平分线的性质、全等三角形的判定与性质．由已知证明△ABD≌△CBD是解决的关键．12．如图，BD是∠ABC的平分线，DE⊥AB于E，S=90，AB=18，BC=12，求DE的长．△ABC【考点】角平分线的性质．【分析】过点D作DF⊥BC于F，根据角平分线上的点到角的两边的距离相等可得DE=DF，然后根据三角形的面积列出方程求解即可．【解答】解：如图，过点D作DF⊥BC于F，∵BD是∠ABC的平分线，DE⊥AB，∴DE=DF，=AB•DE+BC•DF=90，∴S△ABC即×18•DE+×12•DE=90，解得DE=6．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，三角形的面积，熟记性质并作出辅助线是解题的关键．13．如图．已知在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR ⊥AB于R，AB=7，BC=8，AC=9．（1）求BP、CQ、AR的长．（2）若BO的延长线交AC于E，CO的延长线交AB于F，若∠A=60゜，求证：OE=OF．【考点】角平分线的性质；全等三角形的判定与性质．【分析】（1）根据角平分线性质得出OR=OQ=OP，根据勾股定理起床AR=AQ，CQ=CP，BR=BP，得出方程组，求出即可；（2）过O作OM⊥AC于肘，ON⊥AB于N，求出OM=ON，证出△FON≌△EOM即可．【解答】解：连接AO，OB，OC，∵OP⊥BC，OQ⊥AC，OR⊥AB，∠A、∠B的角平分线交于点O，∴OR=OQ，OR=OP，∴由勾股定理得：AR2=OA2﹣OR2，AQ2=AO2﹣OQ2，∴AR=AQ，同理BR=BP，CQ=CP，即O在∠ACB角平分线上，设BP=BR=x，CP=CQ=y，AQ=AR=z，则x=3，y=5，z=4，∴BP=3，CQ=5，AR=4．（2）过O作OM⊥AC于M，ON⊥AB于N，∵O在∠A的平分线，∴OM=ON，∠ANO=∠AMO=90°，∵∠A=60°，∴∠NOM=120°，∵O在∠ACB、∠ABC的角平分线上，∴∠EBC+∠FCB=（∠ABC+∠ACB）=×（180°﹣∠A）=60°，∴∠FON=∠EOM，在△FON和△EOM中∴△FON≌△EOM，∴OE=OF．【点评】本题考查了角平分线性质和全等三角形的性质和判定的应用，注意：角平分线上的点到角两边的距离相等．。