定积分求面积

定积分求平面图形面积在实际生活中的应用定积分是数学中重要的概念，定积分可以用来计算函数在一定范围（定义域）内的积分值。

它是一种可以用来计算面积或计算曲线积分问题的一种技术。

在实际生活中，定积分用于求解平面图形面积的问题，广泛应用于水利、建筑、航空航天等各个领域。

首先，定积分可以用于求解椭圆面积的问题。

椭圆面积可以用定积分来计算，其计算公式为：S=[π/2*(a2-b2)]，其中a是椭圆的长轴，b是椭圆的短轴。

这个公式能够准确地计算出椭圆的面积，在水利等领域中，椭圆管道的运用非常广泛，可以用定积分计算出椭圆管道的面积，从而帮助水利设计者准确地计算水利结构的尺寸。

其次，定积分可以用于求解三角形面积的问题。

三角形的面积也可以通过定积分进行计算，其计算公式为：S=*a*b*sin（C），其中a 和b是三角形的底边，C是三角形的内角。

这个公式可以准确的计算出三角形的面积，在建筑设计等领域中，三角形结构的运用非常广泛，可以用定积分计算出三角形结构的面积，从而帮助设计者准确地计算建筑结构的尺寸。

此外，定积分还可以用于求解复杂图形的面积。

复杂图形的面积可以用定积分来计算，例如可以用定积分计算圆柱体的表面积、圆柱管的表面积以及球的表面积等。

在航空航天等领域中，复杂图形的运用也非常广泛，例如飞机机身的设计、航天器的设计等，可以用定积分计算出复杂图形的面积，从而帮助设计者准确地计算机构的尺寸。

综上所述，定积分在实际生活中极具价值，它可以用于求解椭圆
面积、三角形面积以及复杂图形的面积等问题，在水利、建筑、航空航天等各个领域都有很广泛的应用，其准确的计算方法可以为实际生活中的设计者提供帮助。

找一个函数来描述要求解的曲面一侧的高度，然后描述无穷小单元的面积。

其实，不管是什么样的坐标，思路都是一样的。

事实上，最原始的方法可以用方格子图纸来计算面积。

用定积分计算平面图形的面积、旋转体的体积和平面曲线的弧长。

Mbth是一种积分，它是函数f(X)在区间[a，b]上的积分和的极限。

这里要注意定积分和不定积分的关系：如果有定积分，就是一个具体的数值，而不定积分是一个函数表达式，只有一个数学计算关系(牛顿-莱布尼兹公式)。

定积分定义：设函数f(X)在区间[a，b]上连续，将区间[a，b]分成n个子区间[x0，x1]，(x1，x2]，(x2，x3]，…。

，(xn-1，xn]，其中x0=a，xn=b。

可以知道，每个区间的长度依次为x1=x1-x0，并且每个子区间(xi-1，xi]中的任意点ξi(1，2，…，n)被用作求和公式。

这个求和公式称为积分和。

设λ=max{x1，x2，…，xn}(即，λ是最大间隔长度)。

如果当λ→为0时存在积分和极限，则这个极限称为函数f(X)在区间[a，b]上的定积分，记为，函数f(X)在区间[1]内，其中：a称为积分下限，b称为积分上限，区间[a，b]称为积分区间，函数f(X)称为被积函数，x称为积分变量，f(X)dx称为被积函数表达式，∫称为整数。

之所以叫定积分，是因为积分后得到的值是定的，是常数，不是函数。

根据上述定义，如果函数f(X)可以在区间[a，b]内积分，则存在n等分的特殊除法：特别地，根据上述表达式，当区间[a，b]恰好是区间[0，1]时，区间[0，1]的积分表达式如下：1.当a=b时，2.当a>b时，3.在整数前可以提到常量。

4.代数和的积分等于积分的代数和。

5.定积分的可加性：如果将积分区间[a，b]分成两个子区间[a，c]和[c，b]，则有由于性质2，如果f(X)在区间d上可积，则区间d(可能不在区间[a，b]上)中的任何c都满足条件。

6.如果f(X)在区间[a，b]内≥0。

利用定积分求平面图形面积的一些讨论在数学中，定积分是一个非常重要的概念。

它可以用来求曲线下面的面积、体积等。

在这篇文章中，我们将探讨如何利用定积分来求解平面图形的面积，并对其中的一些需要注意的问题进行讨论。

一、定积分求平面图形的面积通常情况下，我们使用定积分求解平面图形的面积主要分为以下两种情况：1. 若平面图形位于第一象限内，我们可以通过将其关于x轴或y轴进行对称，得到其关于某条轴的镜像图形。

然后，我们可以通过积分的方法求得该镜像图形的面积，再将其乘以2即可得到原图形的面积。

2. 若平面图形位于第三象限内，我们可以采用类似的方法，将其关于x轴和y轴进行对称，再将其平移至第一象限内，最后采用积分的方法求解面积。

二、需要注意的问题在使用定积分求解平面图形的面积时，我们还需要注意以下几个问题：1. 积分区间的确定在求解平面图形面积时，我们需要确定积分的区间。

通常情况下，这个区间并不是在平面直角坐标系中所表示的图形区域，而应该是其在积分方程中的区间。

因此，在进行计算之前，我们需要先画出该图形和其在积分方程中的区间，并根据图形和区间的特点确定积分的上下限。

2. 导数、微积分的运用在计算过程中，我们经常需要使用导数和微积分知识。

对于不熟悉这些知识的人来说，可能会产生一定的困难。

因此，在进行平面图形面积的计算时，我们需要对相关的导数和微积分知识有一定的了解，才能更好地进行计算。

3. 曲线積分的處理如果题目本身是一个曲线的方程或者是一个参数方程问题，我们还需要先将其转化为参数方程或者直接采用曲线积分的方法来求解。

另外，对于一些复杂的曲线问题，我们可能需要结合掌握一定的计算技巧和方法来进行计算。

三、总结定积分是求解平面图形面积的一个非常好的工具。

在进行计算时，我们需要注意导数、微积分等方面的知识，并结合所求图形的特点来确定积分区间、上下限等参数。

只有在掌握了这些知识和技巧之后，我们才能更好地求解平面图形的面积问题。

圆的面积公式推导过程定积分圆的面积公式推导过程（定积分法）一、建立坐标系。

我们以圆的圆心为原点建立平面直角坐标系。

设圆的半径为r，则圆的方程为x^2+y^2=r^2，即y = ±√(r^2)-x^{2}。

由于圆关于x轴对称，我们只需要计算上半圆的面积，然后乘以2就可以得到整个圆的面积。

上半圆的方程为y=√(r^2)-x^{2}。

二、利用定积分计算面积。

1. 确定积分区间。

对于圆来说，x的取值范围是从-r到r。

2. 计算定积分。

根据定积分的几何意义，函数y = √(r^2)-x^{2}在区间[-r,r]上与x轴所围成的图形的面积S为：S=2∫_0^r√(r^2)-x^{2}dx令x = rsinθ，则dx = rcosθ dθ。

当x = 0时，θ= 0；当x = r时，θ=(π)/(2)。

将x = rsinθ和dx = rcosθ dθ代入积分式可得：S=2∫_0^(π)/(2)√(r^2)-r^{2sin^2θ}· rcosθ dθ =2∫_0^(π)/(2)r√(1 - sin^2)θ· rcosθ dθ=2r^2∫_0^(π)/(2)cos^2θ dθ根据三角函数的二倍角公式cos^2θ=(1 + cos2θ)/(2)，则：S=2r^2∫_0^(π)/(2)(1+cos2θ)/(2)dθ =r^2∫_0^(π)/(2)(1 + cos2θ)dθ =r^2<=ft[θ+(1)/(2)sin2θ]_0^(π)/(2) =r^2<=ft((π)/(2)+ 0-(0 + 0)) =π r^2所以，圆的面积公式为S = π r^2。

定积分求面积
将不规则图形的的边界线用曲线方程表示出来,定积分的上下限就是曲线的端点.用上边界曲线的定积分减去下边界曲线的定积分就是面积!
平面图形的面积有两点需要注意，一个是选择用极坐标计算面积还是选择用极坐标系计算面积，一个是在计算面积是应该注意正负，定积分是有正负的，但是面积都是正的，在理解了定积分的含义之后，要明白计算面积时要加绝对值，或者在负的定积分前加负号，保证计算出来的面积是正的。

今天定积分的几何应用分为两个部分，平面图形的面积和曲边扇形面积，前者是直角坐标系下的，后者是极坐标系下的，所以考专升本的小伙伴们只需要学会前者就可以，考研的小伙伴们两个都要很熟练。

其实，秘诀就是两个字——画图，把图画出来，根据定积分的求面积公式就可以了，注意交点，注意范围，注意被积函数。

今天其实就6道例题，但是我写了很久，因为……图太难画了，图像很简单，但是涂色有点麻烦，想了许久，终于成功得涂成了灰灰的样子，哈哈哈哈~~~相当于又复习了一遍原先学的软件，果然，还是熟能生巧（其实完全可以保存好了之后用画图软件打开，直接填充颜色就可以，但是为了彰显我这个小白的软件技术⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄~~哈哈哈哈~）预告一下明天的内容，明天有出题率很高的旋转体体积，还有考研数学一和数学二要学会的求弧长以及旋转体的侧面积或表
面积。

定积分曲线与面积计算在数学中，定积分是一种重要的数学概念，用于计算曲线与坐标轴之间的面积或曲线的长度。

定积分的应用广泛，尤其在微积分和物理学等领域中起着至关重要的作用。

本文将介绍定积分的定义和性质，并详细说明如何使用定积分来计算曲线与面积。

一、定积分的定义定积分是对一个区间上的函数进行积分运算的结果。

它可以看作是将一个曲线下方的面积划分为无穷多个无穷小的长方形，并将这些长方形的面积相加而得到的极限值。

数学上，定积分通过极限运算来定义。

如果函数f(x)在闭区间[a, b]上连续，则对应的定积分可以表示为：∫[a, b] f(x) dx其中，∫表示积分符号，[a, b]表示积分区间，f(x)为被积函数，dx表示自变量的微小增量。

二、定积分的性质定积分具有以下几个重要的性质：1. 线性性质：对于任意的实数c，d和函数f(x)、g(x)，有：∫[a, b] (c * f(x) + d * g(x)) dx = c * ∫[a, b] f(x) dx + d * ∫[a, b] g(x) dx2. 区间可加性：对于区间[a, c]和区间[c, b]上的函数f(x)，有：∫[a, b] f(x) dx = ∫[a, c] f(x) dx + ∫[c, b] f(x) dx3. 积分上下界交换性：如果函数f(x)在区间[a, b]上连续，则下面两个积分相等：∫[a, b] f(x) dx = ∫[b, a] f(x) dx三、使用定积分计算曲线与面积使用定积分可以计算曲线与坐标轴之间的面积。

具体步骤如下：1. 确定积分区间：首先需要确定曲线与坐标轴之间需要计算面积的区间。

2. 构建被积函数：根据具体情况，将曲线的方程表示为y = f(x)，并构建被积函数f(x)。

3. 计算定积分：将被积函数代入定积分的定义中，并按照定义计算出定积分的值。

举例说明，考虑计算曲线y = x^2和x轴所围成的面积。

首先确定积分区间为[-1, 1]，然后将曲线方程改写为x = y^(1/2)，构建被积函数f(y) = y^(1/2)。

微积分中的定积分与面积计算微积分是数学中的一个重要分支，包含了微分与积分两个方面。

在微积分中，定积分是一个非常重要的概念，它与面积计算密切相关。

本文将介绍定积分的概念、性质，以及如何利用定积分来计算曲线下的面积。

一、定积分的概念与性质定积分是微积分中的一个基本概念，它可以用来计算曲线与坐标轴之间的面积。

在数学中，定积分可以看作是一个函数在某个区间上的加权平均值。

具体来说，对于一个函数f(x)，我们可以将其分割成无穷多个小区间，每个小区间的长度为Δx。

然后，我们计算每个小区间上的函数值f(x)乘以Δx的乘积，并将所有乘积相加。

当Δx趋近于0时，这个和就收敛于一个确定的值，即定积分。

定积分的符号表示为∫f(x)dx，其中f(x)为被积函数，dx表示积分变量。

定积分的计算可以通过积分的定义和一系列的积分性质来完成。

其中，积分的定义是通过极限的概念来定义的，即∫f(x)dx = lim(Δx→0) Σf(x)Δx定积分具有一些重要的性质，包括线性性质、区间可加性、保号性等。

线性性质指的是定积分具有加法和数乘的性质，即∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx。

区间可加性指的是对于一个函数在不同区间上的定积分，可以将其分割成多个小区间的定积分的和。

保号性指的是如果一个函数在一个区间上恒大于等于0，则其定积分也大于等于0。

二、利用定积分计算曲线下的面积定积分与面积计算密切相关，可以用来计算曲线与坐标轴之间的面积。

具体来说，对于一个函数f(x)，我们可以通过定积分来计算其在某个区间[a, b]上的面积。

计算方法如下：1. 首先，我们需要确定被积函数f(x)以及积分的区间[a, b]。

2. 将区间[a, b]分成无穷多个小区间，每个小区间的长度为Δx。

3. 在每个小区间上选择一个代表点xi，计算对应的函数值f(xi)。

4. 计算每个小区间上的函数值f(xi)乘以Δx的乘积，并将所有乘积相加。

积分面积公式
积分求面积公式：s=（1，e）-∫（1，e）xd（lnx）。

积分是微积分学与数学分析里的一个核心概念。

通常分为定积分和不定积分两种。

直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。

微积分（Calculus），数学概念，是高等数学中研究函数的微分（Differentiation）、积分（Integration）以及有关概念和应用的数学分支。

它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。

微分学包括求导数的运算，是一套关于变化率的理论。

它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。

积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

定积分可以用来求面积，但定积分不等于面积，因为定积分可以是负数但面积是正的，因此，当所求积分的曲线跨越x轴时，需分段，分大于零和小于零分别计算，然后正的积分加上负的积分的绝对值，就等于面积。

面积是表示平面中二维图形或形状或平面层的程度的数量。

表面积是三维物体的二维表面上的模拟物。

面积可以理解为具有给定厚度的材料的量，面积是形成形状的模型所必需的。

一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。

一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。

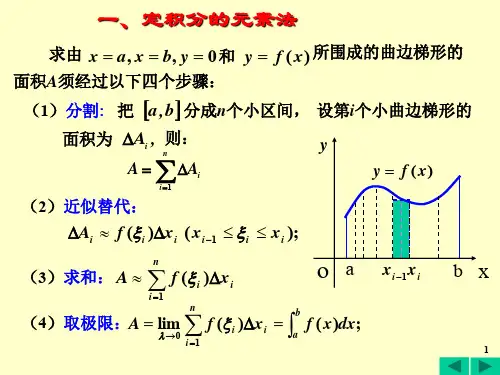
定积分就是求函数f(X)在区间[a，b]中的图像包围的面积。

即由y=0，x=a，x =b，y=f(X)所围成图形的面积。

这个图形称为曲边梯形，特例是曲边三角形。

定积分是把函数在某个区间上的图象[a，b]分成n份，用平行于y轴的直线把其分割成无数个矩形，再求当n→+∞时所有这些矩形面积的和。

定积分与不定积分看起来风马牛不相及，但是由于一个数学上重要的理论的支撑，使得它们有了本质的密切关系。

把一个图形无限细分再累加，这似乎是不可能的事情，但是由于这个理论，可以转化为计算积分。

定积分和面积的关系
嘿，你知道吗，定积分和面积那可是有着超级紧密的关系啊！咱就说那曲线下的面积，定积分就能把它给算出来呢！比如说吧，就像你要知道一个操场的面积，那定积分就像个厉害的工具，能帮你精确地找到这个面积呀！这多神奇呀！
定积分呢，就像是一把神奇的钥匙，能打开面积这个神秘之门。

好比你有一个形状古怪的图形，看着头都大了，不知道它面积咋算，这时候定积分就闪亮登场啦，嘿，能轻松搞定它的面积！比如说一个弯弯绕绕的曲线围成的区域，定积分就能给你算得明明白白！这不是很牛吗？
你想想啊，要是没有定积分，咱要算那些奇奇怪怪图形的面积得多费劲啊！所以说定积分和面积的关系，那真的是太重要啦，就如同好朋友一样，相互成就啊！你这下能明白它们的关系有多铁了吧！。