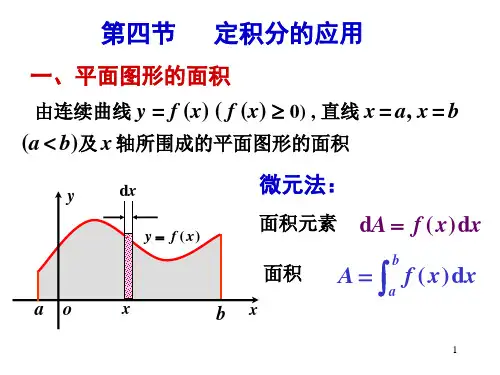
定积分的应用平面图形面积

定积分求平面图形面积在实际生活中的应用定积分是数学中重要的概念，定积分可以用来计算函数在一定范围（定义域）内的积分值。

它是一种可以用来计算面积或计算曲线积分问题的一种技术。

在实际生活中，定积分用于求解平面图形面积的问题，广泛应用于水利、建筑、航空航天等各个领域。

首先，定积分可以用于求解椭圆面积的问题。

椭圆面积可以用定积分来计算，其计算公式为：S=[π/2*(a2-b2)]，其中a是椭圆的长轴，b是椭圆的短轴。

这个公式能够准确地计算出椭圆的面积，在水利等领域中，椭圆管道的运用非常广泛，可以用定积分计算出椭圆管道的面积，从而帮助水利设计者准确地计算水利结构的尺寸。

其次，定积分可以用于求解三角形面积的问题。

三角形的面积也可以通过定积分进行计算，其计算公式为：S=*a*b*sin（C），其中a 和b是三角形的底边，C是三角形的内角。

这个公式可以准确的计算出三角形的面积，在建筑设计等领域中，三角形结构的运用非常广泛，可以用定积分计算出三角形结构的面积，从而帮助设计者准确地计算建筑结构的尺寸。

此外，定积分还可以用于求解复杂图形的面积。

复杂图形的面积可以用定积分来计算，例如可以用定积分计算圆柱体的表面积、圆柱管的表面积以及球的表面积等。

在航空航天等领域中，复杂图形的运用也非常广泛，例如飞机机身的设计、航天器的设计等，可以用定积分计算出复杂图形的面积，从而帮助设计者准确地计算机构的尺寸。

综上所述，定积分在实际生活中极具价值，它可以用于求解椭圆
面积、三角形面积以及复杂图形的面积等问题，在水利、建筑、航空航天等各个领域都有很广泛的应用，其准确的计算方法可以为实际生活中的设计者提供帮助。

第十章 定积分的应用§1 平面图形的面积在上一章开头讨论过由连续曲线()()0≥=x f y ，以及直线()b a b x a x <==,和x 轴所为曲边梯形的面积为()⎰⎰==ba b a ydx dx x f A .|| 如果()x f 在[]b a ,上不都是非负的,则所围图形的面积为()⎰⎰==ba b a dx y dx x f A .|||| 一般地，由上、下两条连续曲线()x f y 2=与()x f y 1=以及两直线a x =与()b a b x <=所围成平面图形（图10－1），它的面积计算公式为()[()].12dx x f x f A ba ⎰-= （1） 图10－1 图10－2例１ 求抛物线x y =2与直线032=--y x 所围图形的面积A ．解 该平面图形如图10-2所示．先求出抛物线与直线的交点()1,1-P 与()3,9Q ．用1=x 把图像分为左、右两部分，应用公式（1）分别球的它们的面积为 [()]⎰⎰==--=10101,342dx x dx x x A .32823912=⎪⎭⎫ ⎝⎛--=⎰dx x x A 所以.33221=+=A A A 本题也可以把抛物线方程和直线方程改写成()()[].3,1,232,12-∈=+===y y g y x y g y x并改取积分变量为y ，便得()()[]dy y g y g A ⎰--=3112().33232312=-+=⎰-dy y y设曲线C 由参数方程 ()()[]βα,,,∈==t t y y t x x （2）给出，在[]βα,上()t y 连续，()t x 连续可微且()0≠'t x （对于()t y 连续可微且()0≠'t y 的情形可类似的讨论）.记()()()(),,0a b b a x b a x a t y <<==≠'或β则由曲线C 及直线x b x a x 和==,轴所围成的面积的图形，其面积计算公式为()().||dt t x t y A '=⎰βα （3）例2 求由摆线()()()0cos 1,sin >-=-=a t a y t t a x 的一拱与x 轴所为平面图形（图10-3）的面积图10-3解 摆线的一拱可取[]π2,0∈t .所求面积为()()[]dt t t a t a A '--=⎰sin cos 120π()222023cos 1a dt t a a ππ=-=⎰.如果由参数方程（2）所标示的曲线是封闭的，即有 ()()()(),,ββy a y x a x ==且在[]βα,内曲线自身不在相交，那么有曲线自身所围图形的面积为()()||dt t x t y A '=⎰βα()().||⎪⎭⎫ ⎝⎛'⎰dt t x t y βα或此公式可由公式（1）和公式（3）推出，绝对值内的积分，其正、负由曲线（2）的旋转方向所确定.例3 求椭圆12222=+by a x 所围的面积. 解 化椭圆为参数方程[].2,0,sin ,cos π∈==t t y t a x由公式（4），求得椭圆所围面积为()|cos sin |20dt t a t b A '=⎰π.sin 202ab tdt ab ππ==⎰显然，当r b a ==时，这就等于圆面积.2r π设曲线C 由极坐标方程()[]βαθθ,,∈=r r给出，其中()θr 在[]βα,上连续，.2παβ≤-由曲线C 与两条射线βθαθ==,所围成的平面图形，通常也可称为扇形（图10-4）.此扇形的面积算公式为().212θθβαd r A ⎰= （5）图10-4 图10-5这任可由定积分的基本思想而得.如图10-5所示，对区间[]βα,作任意分割,:110βθθθθ=<<<<=-n n a T射线()1,,2,1-==n i i θθ把扇形分成n 个小扇形.由于()θr 是连续的，因此当||||T 很小时，在每一个[]i i i θθ,1-=∆上()θr 的值变化也很小.任取i i ∆∈ξ，便有()().,,2,1,,0n i r r i i =∆∈≈θξ这时，第i 个小扇形的面积(),212i i i r A θξ∆≈∆ ()∑=∆≈n i i i r A 12.21θξ由定积分的定义和连续函数的可积性，当0||||→T 时，上式右边的极限即为公式（5）中的定积分.例4 求双曲线θ2cos 22a r =所围平面图形的面积. 解 如图10-6所示，因为,02≥r 所以θ的取值范围是⎥⎦⎤⎢⎣⎡-4,4ππ与.45,43⎥⎦⎤⎢⎣⎡-ππ由图形的对称性及公式（5），得到 ⎰⋅=4022cos 214πθθd a A =.|2cos 2402a a =πθ 图10-6§2 由平行截面面积求体积设Ω为三围空间中的一立体，它夹在垂直于x 轴的两平面a x =与b x =之间).(b a <为方便起见称Ω位于[]b a ,上的立体.若在任意一点[]b a x ,∈处做垂直于x 轴的平面，它截得 Ω的截面面积显然是x 的函数，记为()x A ，[]b a x ,∈，并称之为Ω的截面面积函数（见图10-8）.本节将导出由截面面积函数求立体体积的一般公式和旋转体的体积公式. 图10-8设截面面积函数()x A 是[]b a ,上的一个连续函数，对[]b a ,作分割.:10b x x x a T n =<<=过个分割点做垂直x 轴的平面,,2,1,n i x x i ==它们把Ω切割成n 个薄片.设()x A 在每个小区间[]i i x x i ,1-=∆的最大、小值分别为i M 与i m ，那么每一薄片的体积i V ∆满足 .i i i i i x M V x m ∆≤∆≤∆于是，Ω的体积∑=∆=n i i V v 1满足 .11∑∑==∆≤≤∆n i i i n i i ix M V x m因为()x A 为连续函数，从而在[]b a ,上可积，所以当||||T 足够小时，能使(),11ε<∆-=∆∑∑==n i i i i n i ii x m M x w其中ε为任意小的正数.由此知道⎪⎭⎫ ⎝⎛∆∆=∑∑=→=→n i i i T ni i i T x m x M V 10||||10||||lim lim 或 (),lim 10||||∑=→∆=n i i i T x A ξ其中()()i i i m M A 或=ξ，所以有 ().dx x A V b a ⎰= （1）例1 求两个圆柱面222222a x z a y x =+=+与所围立体的面积.解 图10-9所示为该立体在第一卦限部分的图像（占整体的八分之一）.对任一[]a x ,00∈，平面0x x =与这部分立体的截面是一个边长为202x a -的正方形，所以()x A []..,0,22dx a x x a ∈-=由公式（1）便得().31683022a dx x a V a =-=⎰ 例2 求由椭圆面1222222=++cz b y a x 所为立体的体积. 解 以平面()a x x x ≤=||00截椭球面，得椭圆（它在yOz 面上的正投影）：.1112202222022=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-a x c z a x b y所以截面面积函数为（根据§1例3）：()[].,,122a a x a x bc x A -∈⎪⎪⎭⎫ ⎝⎛-=π于是求得椭圆体积.34122abc dx a x bc V aa ππ=⎪⎪⎭⎫ ⎝⎛-=⎰- 显然当r cb a ===时，这就等于球的体积.343r π 设B A ΩΩ,位于同一区间[]b a ,上的两个立体，其体积分别为.,B A V V 若在[]b a ,上它们的截面面积函数()()x B x A 与皆连续，且()()x B x A =，则有公式（1）推知.B A V V =这个关于截面面积相等则体积也相等的原理，早已为我国齐梁时代的数学家祖冲之之子，生卒年代约在公园5世纪末至6世纪初）在计算球的体积时所发现.在《九章算术》一书中所记载的组原理是：“夫叠基成立积，缘幂势既同则积不可容异”，其中幂就是截面面积，势就是高，这就是说，等高处的截面面积既然相等，则两立体的体积不可能相等（图10-10）.17世纪意大利数学家卡伐列利也提出了类似的原理，但要比组完一千多年.下面讨论旋转体的体积设f 是[]b a ,上的连续函数，Ω是由平面图形()b x a x f y ≤≤≤≤|,|||0绕x 轴旋转一周所得的旋转体，那么易之截面面积函数为()()[][].,,2b a x x f x A ∈=π 由公式（1），得到旋转体Ω的体积公式为()[].2dx x f V π=例3 使用公式（2）导出圆锥体的体积公式.解 设正圆锥的高为h ，地圆半径为r .如图10-11所示，这圆锥体可由平面图形[]h x x h r y ,0,||0∈≤≤绕x 轴旋转一周而得，所以其体积为 ,31220h r dx x h r V h ππ=⎪⎭⎫ ⎝⎛=⎰ 这个结果读者在中学课本便熟知了，又因同底同高的两个圆锥，在相同高程处的截面为相等的圆，及截面面积函数相同，所以任意高为h ，底半径为r 的圆锥（正或斜），其体积恒为.312h r π 例4 求圆()()R r r R y x <<≤-+0222绕x 轴旋转一周所得的环状立体的体积. 解 如图10-12所示，圆()222r R y x =-+的上、下半圆分别为 (),222x r R x f y -+==().||,221r x x r R x f y ≤--==故圆环体的截面面积函数是()()[]()[]2122x f x f x A ππ-= [].,,422R r x x r R -∈-=π图10-11 图10-12由此得到圆环体的体积为.2822022R r dx x r R V rππ⎰=-=如果把上述改写成,22r R ππ⋅读者不难看出这相当于一个圆锥体的体积.§3 平面曲线的弧长与曲率一 、平面曲线的弧长先建立曲线弧长的概念.设平面曲线.AB C =如图10-14所示，在C 上从A 到B 依次去分点：,,,,,1210B P P P P P A n n ==-它们成为对曲线C 的一个分割，记为T.然后用线段连结T 中每相邻两点，得到C 的n 条弦(),,2,11n i P P i i =-这n 条弦又成为C 的一条内接折线,记|,||,|max ||||1111P P st P P T i ni i n i -=-≤≤∑== 分别表示最长弦的长度和折线的总长度.定义1 对于曲线C 的无论怎样的分割T ，如存在有限极限,lim 0||||s st T =→则曲线C 是可求长的，并把极限s 定义作为曲线C 的弧长.定义2 设平面曲线C 由参数方程()()[]βα,,,∈==t t y y t x x给出.如果()t x 与()t y 在[]βα,上连续可微，且()t x '与()t y '不同时为零（即()()[]βα,,022∈≠'+'t t y t x ），则称C 为一条光滑曲线.定理10-1 设曲线C 由参数方程（1）给出，若C 为一条光滑曲线，则C 是可求长的，且弧长为 ()()⎰'+'=βα.22dt t y t x s证 如前所述，对C 作任意分割{},,,10n P P P T =并设0P 与n P 分别对应βα==t t 与，且 ()()()().1,,2,1,,,-==n i ti y ti x yi xi P i 于是，与T 对应的得到区间[]βα,的一个分割β=<<<<<='-n n o t t t t t a T 121:在T '所属的每个小区间[]i i t t i ,1-=∆上，由微分中值定理得()()().,1i i i i i i i t x t x t x x ∆<∆'=-=∆-ξξ()()().,1i i i i i i i t y t y t y y ∆<∆'=-=∆-ηη 从而曲线C 内接折线总长为.122∑=∆+∆=n i i i y x sT()().122t y x i n i i ∆'+'=∑=ηξ又因C 为光滑曲线，当()0≠'t x 时，在t 的某领域内()t x x =有连续的反函数，故当0→∆x 时0→∆t ；类似的，当()0≠'t y 时，亦能由0→∆y 推知0→∆t .所以当0|1|22→∆+∆=-i i i i y x P P 时，必有0→∆i t .反之，当0→∆i t 时，显然有.0|1|→-i i P P 由此知道；当C 为光滑曲线时，0||||→T 与0||||→'T 是等价的.由于()()t y t x 22'+'在[]βα,上连续从而可积，因此根据定义1，只需证明：()(),lim lim 1220||||0||||∑=→→∆'+'=n i i t t t i y i x sT ξξ （3）而后者即为（2）式右边的定积分，为此记()()()()i i i y i x y i x ξξηξσ2222'+'-'+'=则有 ()()[].122t y i x sT i n i i ∆+'+'=∑=σξξ利用三角形不等式易证()()()()|,|||||||||i i i i i y y y y ξηξησ'-'≤'-'≤由()t y '在[]βα,上连续，从而一致连续，故对任给的,0>ε存在,0>δ当δ<'||||T 时，只要i ξ、,i i ∆∈η就有.,,2,1,||n i i =-<αβεσ因此有 ()()∑∑--∆=∆'+'-n i i i i n i i t t y i x sT 1122||||σξξ∑-<∆≤n i i i t 1.||εσ即（3）式得证，亦即公式（2）成立.若曲线C 有直角坐标方程()[]b a x x f y ,,∈=表示，把它看做参数方程时，即为()[].,,,b a x x f y x x ∈==所以当()x f 在[]b a ,上连续可微时，此曲线即为一光滑曲线.这时弧长公式为 ()⎰'+=ba dx x f s .12 （4）又若曲线C 由极坐标方程()[]βαθθ,,∈=r r表示，把它化为参数方程，则为()()[]βαθθθθθ,,cos ,cos ∈==r y r x()()(),sin cos θθθθθr r x -'='()()(),cos sin θθθθθr r y '+='()()()(),2222θθθθr r y x '+='+'因此，当()θr '在[]b a ,上连续，且()θr '与()θ2r '不同时为零时，此极坐标曲线为一光华曲线.这时弧长公式为 ()().22θθθβαd r r s ⎰'+= （5）例1 求摆线()()()0cos 1,sin >-=-=a t a y t t a x 一拱的弧长（见图10-3）。

定积分求平面图形面积在实际生活中的应用把复杂的积分问题求解出来就可以计算出平面图形的面积，在实际生活中也可以看到它的很多应用。

其中有一类是涉及设计的，比如建筑设计中的空间分配、土地开发等；另一类是分析的，比如海洋表面的波浪分析等。

1、建筑设计建筑设计中，定积分可以用来求解空间分配问题。

比如，在房屋设计中，它可以用来确定楼层、楼梯、墙壁、门窗等占用了多少面积。

此外，它还可以用来求解不规则房间布局时，室外墙体和室内墙体的面积分配。

同样，在土地开发中也可以看到定积分的应用，如计算出道路两端的封闭区域面积，以及计算建筑的总面积。

定积分也可以帮助规划者精确计算出规划区域的面积，从而更好地管理规划区域的开发。

2、海洋表面的波浪分析定积分也可以用来求解海洋表面的波浪。

水波的主要性质是在洋流中运动，它的变化符合泊松方程，这是一个带积分的方程，可以用定积分来求解。

这种波浪分析可以更好地解释海洋表面的复杂性，进而指导航管理者和建筑者采取更安全有效的导航措施。

此外，在海岸线上，可以使用定积分来计算海岸线内各子区域的面积，以及海岸线及其各个部分的面积，为海洋管理者提供有形的参考数据。

3、农业此外，定积分在农业中也有非常广泛的应用。

比如，在种植作物时，可以使用定积分来计算出作物地的面积，以及需要灌溉地区的面积；在研究农田开发时，可以利用定积分来计算出耕作面积。

通过计算出具体的面积数据，可以更好地规划农田的分布和种植规模，从而节约农业资源，提高农作物的产量。

总结定积分是一种有用的数学技术，可以把复杂的数学问题转化成计算机可计算的简单形式，在计算平面图形面积上表现出很强的优势。

它在实际生活中有很多应用，比如建筑设计、土地开发、海洋洋面波浪分析，以及农业规划等。

定积分的几何应用定积分是微积分中的重要概念，它有着广泛的应用。

其中之一就是在几何学中的应用。

本文将探讨定积分在几何学中的具体应用，并解释其背后的原理和意义。

一、平面图形的面积通过定积分，我们可以计算出复杂平面图形的面积。

假设有一个曲线方程y=f(x)，该曲线与x轴所围成的图形为A。

我们可以将A分解成无限个极小的矩形条，然后通过求和的方式来逼近A的面积。

具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。

然后，在每个小区间中，选择一个x值作为代表点，记作xi。

根据代表点xi和函数f(x)的值，我们可以计算出相应小矩形的高度为f(xi)。

由于每个小矩形的宽度Δx非常小，因此在计算总面积时，可以通过求和的方式逼近。

即可以得到如下的定积分表达式：A = ∫[a,b] f(x) dx其中[a,b]表示x的取值范围。

通过对上述定积分进行求解，即可得到图形A的面积。

二、曲线的弧长除了计算平面图形的面积外，定积分还可以用来计算曲线的弧长。

假设有一个曲线L，其方程为y=f(x)。

我们希望计算出曲线L的弧长。

与计算面积类似，我们同样可以将曲线L分解为无限个极小的线段，然后通过求和的方式来逼近曲线L的弧长。

具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。

然后，在每个小区间中，选择一个x值作为代表点，记作xi。

根据代表点xi和函数f(x)的值，我们可以计算出相应线段的长度为Δs。

同样地，由于每个小线段的长度Δs非常小，因此在计算总弧长时，可以通过求和的方式逼近。

即可以得到如下的定积分表达式：L = ∫[a,b] √(1 + [f'(x)]^2) dx其中[a,b]表示x的取值范围，f'(x)表示函数f(x)的导数。

通过对上述定积分进行求解，即可得到曲线L的弧长。

三、体积与质量除了平面图形的面积和曲线的弧长外，定积分还可以用来计算体积和质量。

当我们需要计算一个曲线绕某个轴旋转一周所形成的立体的体积时，定积分就派上用场了。

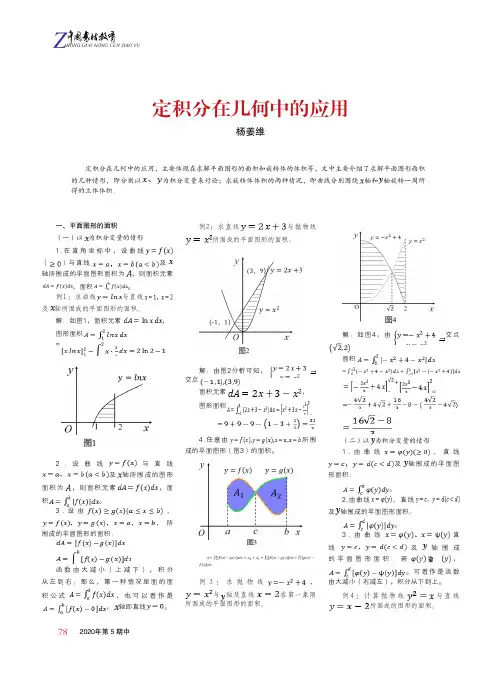
782020年第 5 期中定积分在几何中的应用杨姜维一、平面图形的面积（一）以为积分变量的情形1.在直角坐标中，设曲线（）与直线及轴所围成的平面图形面积为，则面积元素，面积。

例1：求曲线与直线及轴所围成的平面图形的面积。

解：如图1，面积元素，图形面积=2.设曲线与直线及轴所围成的图形面积为，则面积元素，面积。

3.设由，所围成的平面图形的面积：函数由大减小（上减下），积分从左到右；那么，第一种情况里面的面积公式，也可以看作是，轴即直线。

例2：求直线与抛物线所围成的平面图形的面积。

解：由图2分析可知，交点面积元素，图形面积4.任意由所围成的平面图形（图3）的面积。

例3：求抛物线，与轴及直线在第一象限所围成的平面图形的面积。

解：如图4，由交点面积+（二）以为积分变量的情形1.由曲线、直线及轴围成的平面图形面积：。

2.由曲线、直线及轴围成的平面图形面积：。

3.由曲线直线及轴围成的平面图形面积：若，。

可看作是函数由大减小（右减左），积分从下到上。

例4：计算抛物线与直线所围成的图形的面积。

定积分在几何中的应用，主要体现在求解平面图形的面积和旋转体的体积等，文中主要介绍了求解平面图形面积的几种情形，即分别以为积分变量来讨论；求旋转体体积的两种情况，即曲线分别围绕轴和轴旋转一周所得的立体体积。

JIAO HAI TAN HANG／教海探航解：如图5，由交点为方便计算，选取为积分变量，则有4.任意由曲线直线及轴围成的平面图形面积：。

二、旋转体的体积一个平面图形围绕其所在平面上的一条直线旋转一周而成的立体即为旋转体，常见的旋转体有圆柱体、圆锥、圆台、球体等,这些都有对应的体积公式，面对日常生活中所用到的水杯、花瓶等立体物件，求解体积时可考虑以下情况：（一）曲线绕轴旋转的情形由连续曲线与直线及轴所围成的曲边梯形绕轴旋转一周而成的立体，选为积分变量，该旋转体的体积元素，体积为。

（二）曲线绕轴旋转的情形由曲线、直线及轴围成的平面图形绕轴旋转一周所得的立体，选为积分变量，该旋转体的体积元素，体积为。

第十章 定积分的应用 1 平面图形的面积公式1：连续曲线y=f(x)(≥0)，以及直线x=a, x=b(a<b)和x 轴所围曲边梯形面积为：A=⎰b a f(x )dx=⎰ba y dx.若f(x)在[a,b]变号，则所围图形的面积为：A=⎰b a |f(x )|dx=⎰ba |y |dx.公式2：上下两条连续曲线y=f 2(x)与y=f 1(x)以及两条直线x=a 与x=b(a<b)所围的平面图形面积为：A=⎰ba 12(x )]-f (x )[f dx.例1：求由抛物线y 2=x 与直线x-2y-3=0所围图形的面积A. 解法一：A 等同于由抛物线y=x 2与直线y=2x+3所围图形的面积. 解方程组：⎩⎨⎧=+= x y 32x y 2，得⎩⎨⎧==9y 3x , ⎩⎨⎧=-=1y 1x . ∴A=⎰-+312)x -3(2x dx=[32-(-1)2]+3[3-(-1)]-3(-1)-333=332. 解法二：如图，图形被x=1分为左右两部分， A 左=⎰--10)]x (x [dx=3⎰10x dx=34. A 右=⎰⎪⎭⎫ ⎝⎛-9123-x x dx=312-9233-41-922+21)-(93⨯=328. A= A 左+ A 右=34+328=332.公式3：设曲线C 为参数方程x=x(t), y=y(t), t ∈[α,β]，在[α,β]上y(t)连续，x(t)连续且可微且x ’(t)≠0(类似地可讨论y(t)连续可微且y ’(t)≠0的情形). 记a=x(α), b=x(β), (a ≠b)，则由曲线C 及直线x=a, x=b 和x 轴所围的图形，其面积计算公式为：A=⎰'βα(t)x )t (y dt.例2：求由摆线x=a(t-sint), y=a(1-cost) (a>0)的一拱与x 轴所围平面图形的面积.解：摆线的一拱可取t ∈[0,2π]，又x ’=a(1-cost)， ∴A=⎰-2π022)t cos 1(a dt=3πa 2.公式4：若参数方程所表示的曲线是封闭的，即有x(α)=x(β), y(α)=y(β)， 且在(α,β)内曲线自身不再相交，则由曲线自身所围图形面积为： A=⎰'βα(t)dt x )t (y 或A=⎰'βα(t)dt y )t (x .例3：求椭圆22a x +22by =1所围的面积.解：化为参数方程：x=asint, y=bcost, t ∈[0,2π], 又x ’=acost ， ∴A=⎰2π02tdt abcos =πab.公式5：设曲线C 为极坐标方程r=r(θ), θ∈[α,β]，且r(θ)在[α,β]上连续, β-α≤2π.由曲线C 与两条射线θ=α, θ=β所围成的平面图形，通常也称为扇形，此扇形的面积为：A=⎰βα2d θ)θ(r 21. 证：如图，对区间[α,β]作任意分割T ：α=θ0<θ1<…<θn-1<θn =β， 射线θ=θi (i=1,2,…,n-1)把扇形分成n 个小扇形.∵r(θ)在[α,β]上连续，∴当T 很小时，在每一个△i =[θi-1, θi ]上r(θ)的值变化也很小，任取ξi ∈△i ，便有r(θ)≈r(ξi ), θ∈△i , i=1,2,…,n.这时，第i 个小扇形的面积△A i ≈21r 2(ξi)△θi , ∴A ≈∑=n1i 21r 2(ξi )△θi .当T →0时，两边取极限，就有A=⎰βα2d θ)θ(r 21.例3：求双纽线r 2=a 2cos2θ所围平面图形的面积. 解：如图，∵r 2≥0，∴θ∈[-4π,4π]∪[43π,45π]，由图形的对称性可得： A=4·⎰4π02θdθ2cos a 21=a 2 sin2θ|4π0=a 2 .习题1、求由抛物线y=x 2与y=2-x 2所围图形的面积.解：求得两曲线交点为(-1,1), (1,1). ∴所围图形的面积为： A=⎰-1122)x -x -(2dx=38.2、求曲线y=|lnx|与直线x=101, x=10, y=0所围图形的面积. 解：所围图形的面积为： A=⎰10101|lnx |dx=-⎰1101lnx dx+⎰101lnx dx =-(xlnx|1101-⎰1101x dlnx)+ xlnx|101+⎰101x dlnx=-(101ln10-109)+10ln10-9=1099ln10-1081.3、抛物线y 2=2x 把圆x 2+y 2=8分成两部分，求这两部分面积之比. 解：问题等同于抛物线y=21x 2把圆x 2+y 2=8分成两部分，求面积比. 它们的交点为(2,2),(-2,2). 记两部分的面积为A 1,A 2，则A 1=⎰--2222)x 21x -8(dx=8⎰-4π4π2θcos d θ-38=2π+34；A 2=8π-A 1=6π-34.∴21A A =34-6π34+2π=2 -9π2 +3π.4、求内摆线x=acos 3t, y=asin 3t (a>0)所围图形的面积. 解：如图，所围图形面积为： A=4⎰'2π033dt |)t t(asin cos a |=12a2⎰2π024tdttsin cos=12a 2⎰2π024tdt tsin cos =83πa 2.5、求心形线r=a(1+cos θ) (a>0)所围图形的面积. 解法一：根据心形线的对称性，得A=2·⎰+π022d θ)θcos 1(a 21=a 2⎰++π02d θ)θcos θcos 21(=23πa 2.解法二：化为参数方程：x=a(1+cos θ)cos θ, y=a(1+cos θ)sin θ, θ∈[0,2π]， A=|⎰'++2π0d θ]θsin )θcos θ[a(1cos )θcos a(1| =a 2|⎰-+2π0234θ)dθθsin cos θcos 2θcos (2|=23πa 2.6、求三叶形曲线r=asin3θ (a>0)所围图形的面积.解：根根三叶形曲线的形态特点，所围图形由相同的三部分组成，即 A=3⎰32π3π223θsin a 21d θ=⎰32π3π223θsin a 21d3θ=4πa 2.7、求曲线a x +by =1 (a,b>0)与坐标轴所围图形的面积. 解：曲线与x 轴的交点为(a,0)，∴所围图形的面积为： A=b ⎰⎪⎪⎭⎫ ⎝⎛+-a0a x a x 21dx=6ab.8、求曲线x=t-t 3, y=1-t 4所围图形的面积.解：当t=-1,1时，x=0,y=0，∴曲线在t ∈[-1,1]围成封闭图形，即 A=|⎰'-11-43)t -)(1t t (dt|=4|⎰-11-46)t t (dt|=3516.9、求二曲线r=sin θ与r=3cos θ所围公共部分的面积. 解法一：化为圆的方程：x 2+(y-21)2=41, (x-23)2+y 2=43. 它们的交点为O(0,0)与P(43,43)，∴所围公共部分的面积为： A=⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+---⎪⎭⎫ ⎝⎛-4302223y 4321-y 41dy=⎰-6π2π2t cos 41dt+⎰3π02t cos 43dt -833 =323+12π+3233+8π-833=245π-43. 解法二：由sin θ=3cos θ, 得tan θ=3，∴二曲线相交于θ=3π.A=⎰3π02θsin 21d θ+⎰2π3π2θcos 23d θ=-)1(cos2θ413π0-⎰d θ+⎰+2π3π1)(cos2θ43d θ =-163+12π+8π-1633=245π-43.(参考解法)如图：求得P(43,43) S 阴=S P OO 1扇形+S P OO 2扇形-S P OO 1∆ -S P OO 2∆ =3πOO 12+6πOO 22-21·43·OO 1-21·43·OO 2=12π+8π-163-1633=245π-43.10、求两椭圆22a x +22b y =1与22b x +22ay =1(a>b>0)所围公共部分的面积.解：两椭圆在第一象限的交点为：⎪⎪⎭⎫⎝⎛++2222b a abb a ab ，. 根据图形的对称性，可得：A=8⎰+⎪⎪⎭⎫ ⎝⎛--22baab022x a x 1b dx=4abarcsin 22b a b +-2222b a b 4a +.。

第十章 定积分的应用1 平面图形的面积公式1：连续曲线y=f(x)(≥0)，以及直线x=a, x=b(a<b)和x 轴所围曲边梯形面积为：A=⎰b a f(x )dx=⎰ba y dx.若f(x)在[a,b]变号，则所围图形的面积为：A=⎰b a |f(x )|dx=⎰ba |y |dx.公式2：上下两条连续曲线y=f 2(x)与y=f 1(x)以及两条直线x=a 与x=b(a<b)所围的平面图形面积为：A=⎰ba 12(x )]-f (x )[f dx.例1：求由抛物线y 2=x 与直线x-2y-3=0所围图形的面积A.？解法一：A 等同于由抛物线y=x 2与直线y=2x+3所围图形的面积. 解方程组：⎩⎨⎧=+= x y 32x y 2，得⎩⎨⎧==9y 3x , ⎩⎨⎧=-=1y 1x . ∴A=⎰-+312)x -3(2x dx=[32-(-1)2]+3[3-(-1)]-3(-1)-333=332. 解法二：如图，图形被x=1分为左右两部分， A 左=⎰--10)]x (x [dx=3⎰10x dx=34. A 右=⎰⎪⎭⎫ ⎝⎛-9123-x x dx=312-9233-41-922+21)-(93⨯=328. A= A 左+ A 右=34+328=332.:公式3：设曲线C 为参数方程x=x(t), y=y(t), t ∈[α,β]，在[α,β]上y(t)连续，x(t)连续且可微且x ’(t)≠0(类似地可讨论y(t)连续可微且y ’(t)≠0的情形). 记a=x(α), b=x(β), (a ≠b)，则由曲线C 及直线x=a, x=b 和x 轴所围的图形，其面积计算公式为：A=⎰'βα(t)x )t (y dt.例2：求由摆线x=a(t-sint), y=a(1-cost) (a>0)的一拱与x 轴所围平面图形的面积.解：摆线的一拱可取t ∈[0,2π]，又x ’=a(1-cost)， ∴A=⎰-2π022)t cos 1(a dt=3πa 2.公式4：若参数方程所表示的曲线是封闭的，即有x(α)=x(β), y(α)=y(β)， 且在(α,β)内曲线自身不再相交，则由曲线自身所围图形面积为：:A=⎰'βα(t)dt x )t (y 或A=⎰'βα(t)dt y )t (x .例3：求椭圆22a x +22by =1所围的面积.解：化为参数方程：x=asint, y=bcost, t ∈[0,2π], 又x ’=acost ， ∴A=⎰2π02tdt abcos =πab.公式5：设曲线C 为极坐标方程r=r(θ), θ∈[α,β]，且r(θ)在[α,β]上连续, β-α≤2π.由曲线C 与两条射线θ=α, θ=β所围成的平面图形，通常也称为扇形，此扇形的面积为：A=⎰βα2d θ)θ(r 21.证：如图，对区间[α,β]作任意分割T：α=θ0<θ1<…<θn-1<θn=β，<射线θ=θi(i=1,2,…,n-1)把扇形分成n个小扇形.∵r(θ)在[α,β]上连续，∴当T很小时，在每一个△i=[θi-1, θi]上r(θ)的值变化也很小，任取ξi∈△i，便有r(θ)≈r(ξi), θ∈△i, i=1,2,…,n.这时，第i个小扇形的面积△A i≈21r2(ξi)△θi, ∴A≈∑=n1i21r2(ξi)△θi.当T→0时，两边取极限，就有A=⎰βα2dθ)θ(r21.-例3：求双纽线r2=a2cos2θ所围平面图形的面积.解：如图，∵r2≥0，∴θ∈[-4π,4π]∪[43π,45π]，由图形的对称性可得：A=4·⎰4π2θdθ2cosa21=a2 sin2θ|4π=a2 .习题1、求由抛物线y=x2与y=2-x2所围图形的面积.解：求得两曲线交点为(-1,1), (1,1). ∴所围图形的面积为：A=⎰-1122)x-x-(2dx=38.{2、求曲线y=|lnx|与直线x=101, x=10, y=0所围图形的面积. 解：所围图形的面积为：A=⎰10101|lnx |dx=-⎰1101lnx dx+⎰101lnx dx =-(xlnx|1101-⎰1101x dlnx)+ xlnx|101+⎰101x dlnx=-(101ln10-109)+10ln10-9=1099ln10-1081.3、抛物线y 2=2x 把圆x 2+y 2=8分成两部分，求这两部分面积之比. 解：问题等同于抛物线y=21x 2把圆x 2+y 2=8分成两部分，求面积比.：它们的交点为(2,2),(-2,2). 记两部分的面积为A 1,A 2，则A 1=⎰--2222)x 21x -8(dx=8⎰-4π4π2θcos d θ-38=2π+34；A 2=8π-A 1=6π-34.∴21A A =34-6π34+2π=2 -9π2 +3π.4、求内摆线x=acos 3t, y=asin 3t (a>0)所围图形的面积. 解：如图，所围图形面积为： A=4⎰'2π033dt |)t t(asin cos a |=12a2⎰2π024tdttsin cos=12a2⎰2π024tdt tsin cos =83πa 2.【5、求心形线r=a(1+cos θ) (a>0)所围图形的面积. 解法一：根据心形线的对称性，得A=2·⎰+π022d θ)θcos 1(a 21=a 2⎰++π02d θ)θcos θcos 21(=23πa 2.解法二：化为参数方程：x=a(1+cos θ)cos θ, y=a(1+cos θ)sin θ, θ∈[0,2π]， A=|⎰'++2π0d θ]θsin )θcos θ[a(1cos )θcos a(1| =a 2|⎰-+2π0234θ)dθθsin cos θcos 2θcos (2|=23πa 2.,6、求三叶形曲线r=asin3θ (a>0)所围图形的面积.解：根根三叶形曲线的形态特点，所围图形由相同的三部分组成，即 A=3⎰32π3π223θsin a 21d θ=⎰32π3π223θsin a 21d3θ=4πa 2.7、求曲线a x +by =1 (a,b>0)与坐标轴所围图形的面积. 解：曲线与x 轴的交点为(a,0)，∴所围图形的面积为：A=b ⎰⎪⎪⎭⎫ ⎝⎛+-a0a x a x 21dx=6ab .$8、求曲线x=t-t 3, y=1-t 4所围图形的面积.解：当t=-1,1时，x=0,y=0，∴曲线在t ∈[-1,1]围成封闭图形，即 A=|⎰'-11-43)t -)(1t t (dt|=4|⎰-11-46)t t (dt|=3516.9、求二曲线r=sin θ与r=3cos θ所围公共部分的面积.解法一：化为圆的方程：x 2+(y-21)2=41, (x-23)2+y 2=43. 它们的交点为O(0,0)与P(43,43)，∴所围公共部分的面积为： A=⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+---⎪⎭⎫ ⎝⎛-4302223y 4321-y 41dy=⎰-6π2π2t cos 41dt+⎰3π02t cos 43dt -833 =323+12π+3233+8π-833=245π-43. *解法二：由sin θ=3cos θ, 得tan θ=3，∴二曲线相交于θ=3π.A=⎰3π02θsin 21d θ+⎰2π3π2θcos 23d θ=-)1(cos2θ413π0-⎰d θ+⎰+2π3π1)(cos2θ43d θ =-163+12π+8π-1633=245π-43.(参考解法)如图：求得P(43,43) S 阴=S P OO 1扇形+S P OO 2扇形-S P OO 1∆ -S P OO 2∆ =3πOO 12+6πOO 22-21·43·OO 1-21·43·OO 2=12π+8π-163-1633=245π-43.10、求两椭圆22a x +22b y =1与22b x +22ay =1(a>b>0)所围公共部分的面积.解：两椭圆在第一象限的交点为：⎪⎪⎭⎫ ⎝⎛++2222b a abba ab，. 根据图形的对称性，可得：A=8⎰+⎪⎪⎭⎫ ⎝⎛--22baab022x a x 1b dx=4abarcsin 22b a b +-2222b a b 4a +.。