当前位置：文档之家 › 平面波函数

平面波函数

  • 格式：ppt
  • 大小：747.00 KB
  • 文档页数：58

下载文档原格式

  / 58

合集下载

波函数的几种不同的形式

波函数的几种不同的形式

r1 ) 2n
n 0,1,2,3,.....
A Amax A1 A2
干涉减弱 的条件：
( 20
10
)
2
(r2 r1 ) (2n 1)
n 0,1,2,3,.....
A Amin | A1 A2 |
当两波源的初相位相同时，相干条件可写为：为波程差
干涉加强 r2 r1 n n 0,1,2,3,...
t
u
显然能流是随时间周期性变化的。但它总为正值。
2)平均能流:在一个周期内能流的平均值称为平均能流。
P u S
3)能流密度:通过垂直于波动传播方向的单位面积的平均能流 称为能流密度或波的强度。
I P u 1 A2 2u
S
2
能流密度是单位时间内通过垂直于波速方向的单位截面的
平均能量。
I
1
A2
注意： 波的叠加原理仅限于线性波动现象， 例如对强冲击波则不成立。
三、弦上横波的反射与透射
定义媒质特征阻抗: Z u 媒质密度，u 波速
1、振幅
振幅反射系数
B Z1 Z2 A Z1 Z2
A 入射波振幅
振幅透射系数
C 2Z1 A Z1 Z2
B 反射波振幅 C 透射波振幅
2、能量＝1 2 A2 , I 1 2 A2u 1 2 A2 Z
3、驻波的特征： y y1 y2 2 Acos kx cost
①波节和波腹： 有些点不动(波节),有些点振动最强(波腹)
波节：振幅为零的点称为波节。
| 2 Acos 2 x | 0 即: 2 x (2n 1) 的各点。
2
波节的位置为： x (2n 1)
4
n 0, 1, 2y...

波函数的几种不同的形式

波函数的几种不同的形式

C、若 t 一定， E k 、 E p 随 x 周期分布。
D、能量以速度 u 传播。
二、波的能流（描述波的能量传播的物理量）：
1)能流 — 单位时间内垂直通过某一截面的能量。
设波速为u ，在 时t 间内通过垂直于波速截面
E u t S
的Su能量:
S
ε为截面所在位置的能量密度。
能流为：
ut
P E u S uS 2 A2 sin2[(t x )]
cos(t
20
2
r2 )
在 P 点的振动为同方向同频率振动的合成。
y1( p, ty2 ( p, t )
A2
cos(t
20
2
r2 )
由叠加原理P 点合振动：
y y1 y2 Acos(t )
A A12 A22 2 A1 A2 cos
( 20
干涉减弱
r2 r1
(2n 1)
2
n 0,1,2,3,...
[例1]在同一媒质中相距为20m 的两平面简谐波源S1 和S2 作同方
向,同频率(ν=100Hz )的谐振动,振幅均为A=0.05m,点S1 为波峰时,点S2恰为波谷,波速u = 200m / s 。
求：两波源连线上因干涉而静止的各点位置.
y2
Acos[2 (t
20
x)]
因干涉而静止的点的条件为:
[2 (t x 20 ) ] 2 (t x ) (2n 1)
n 0,1,2,
化简上式,得:
x n 10
2
将 u 代2入m,可得:
x n 10(m)
所以在两波源的连线上因干涉而静止的点的位置分别为:
x 1,2,3,,17,18,19m

波函数的复数表示

波函数的复数表示

§3.3 波函数的复数表示 复振幅一．波函数的复数表示简谐函数和复指数函数之间存在着对应关系，可用复指数函数来表示简谐函数。

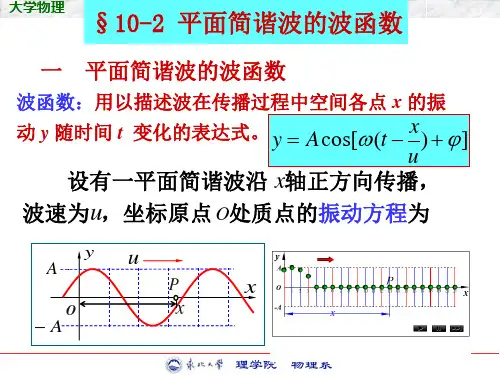
不论复指数函数的实部或虚部都可以用来描写简谐波，习惯上都选用其实部，即余弦函数 平面波波函数为图3.3-1 复数的图示)cos(0),(ϕω+⋅−r k t =A t p E)]}(exp[{0ϕω+⋅−−=r k t i A R e 平面波复数表示：)}(exp{),(0ϕω+⋅−−=r k t i A t p E球面波复数表示：0(,)()exp{()}E p t A r i t k r ωϕ=−−⋅+注意：1．复数表示是对应关系，不是相等关系。

2．作简谐波函数的线性运算（加、减、乘常数、微分、积分）时，可用复指数函数来表示波函数，并通过复数运算后，从计算的最后结果取相应的实部即为所求。

二．复振幅复指数函数表示波函数t i i e Ae t p E ωϕ−−⋅⋅=)(0),(r k 某点在 t 时刻的振动完全由该点的振幅和初相所决定。

平面波场中任一点 P 的复振幅0()()()()()i k r i p Ep A p e A p e φφ•−−== 沿x 方向传播的一维平面波的复振幅为)(0)(~φ−=kz i Ae p E球面波的复振幅为0()()i kr A E p e rφ±−= 强调：相位因子的表示会聚与发散±高斯波束的复振幅为)]())(2(exp[))(exp()()(~0222220z i z r y x z ik z w y x t w A p E φ+++−⋅+−=小结：复振幅是一个复量，其模量表示波场中某点的振幅，其辐角表示该点初相位的负值。

复振幅包含了我们所关心的振幅和相位两个空间分布，所以可以用它来描写单色光波场。

三．共轭波设某一波的复振幅为 r k ⋅=i e p A p E )()(~复共轭函数 ()()i Ep A p e −⋅= k r ——共轭波 意义：共轭波与原波是互为共轭的，它们的实振幅空间分布相同，只是其波矢量由k 变为-k ，即传播方向反转。

《平面波函数》课件

《平面波函数》课件

平面波函数的特性
1
平面波函数具有周期性，即波的振动状态会重复 出现，这是由于波的传播具有周期性。
2
平面波函数的空间形式是平面波，即波的传播方 向与波矢 $mathbf{k}$ 垂直，而振幅在空间中是 均匀分布的。
3
平面波函数的时间形式是简谐振动，即波的振动 形式是正弦或余弦函数，这是由于波动现象通常 是由振源的振动所激发。
奇函数对称性
对于另一些平面波函数，如正切波和余切波，函数图像关于原点对称。这意味着对于任 何实数x，f(x) = -f(-x)成立。
平面波函数的周期性
周期性定义
如果存在一个非零常数T，使得对于定义域内的所有x，f(x + T) = f(x)都成立，则称函数f(x)具有周期 性，T称为其周期。
常见周期函数
应用
在干涉实验中的应用
干涉实验是物理学中常用的实验方法，用于研究波的叠加和 相干性。平面波函数在干涉实验中扮演着重要的角色，因为 干涉现象是波函数相干叠加的结果。通过测量干涉条纹的分 布和变化，可以深入了解波的传播和叠加机制。
在干涉实验中，通常使用激光作为相干光源，其光场可以近 似为平面波函数。通过调整干涉臂的长度和角度，可以改变 干涉条纹的分布，进一步研究波函数的性质。
感谢观看
THANKS
这个表达式描述了波在三维空间中随时间和位置的变化规律，其中 $omega$ 和 $mathbf{k}$ 分别决定了波的频率和传播方向。
平面波函数的物理意义
平面波函数描述了波动现象中各点的 振动状态，它包含了波的振幅、相位 和传播方向等信息。
在物理中，波动是一种广泛存在的现 象，如声波、光波、电磁波等都可以 用平面波函数来描述。
在粒子加速器中的应用

10-2平面简谐波的波函数

10-2平面简谐波的波函数

x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
yO Acost
yO表示质点O在 t时刻离开平衡位置的距离.
考察波线上P点(坐标x), P点比O点的振
动t 落Δ后t 时刻t 的ux,位P移点，在由t此时得刻的位移是O点在
y A
u
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
y
u
A
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
故P点的振动方程（波动方程）为：
y
yo
(t
t)
A cos[ (t
x) u
]
对波动方程的各种形式，应着重从
物理意义上去理解从形式上看：波动是波形的传播.
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
大学物理 §§1100--22 平平面简面谐波简的谐波函波数 的波函数
一 平面简谐波的波函数
波函数：用以描述波在传播过程中空间各点 x 的振
动 y 随时间 t 变化的表达式。 y Acos[(t x) ]
u
设有一平面简谐波沿 x轴正方向传播，
波速为u，坐标原点 O处质点的振动方程为
y A
u
P
uu
Acos[(t x ) ( x0 )]
理学u院 物理u系
大学物理
§10-2 平面简谐波的波函数
例4 一平面简谐波以速度 u 20 m s-1 沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).

《平面波函数》课件

《平面波函数》课件
电磁波
在电磁波理论中，平面波函数用于描述电磁波的传播方式和特性，如无线电波、可见光 和X射线等。这为电磁波的传播、散射和吸收等研究提供了基础。
相对论
在狭义相对论中，平面波函数用于描述光波的传播方式和特性。这为理解光速不变原理 和相对论效应提供了重要的理论基础。
Part
06
深入理解平面波函数的意义和 价值
平面波函数
• 平面波函数的定义 • 平面波函数的图像与特征 • 平面波函数的应用场景 • 平面波函数与其他波动函数的对比 • 平面波函数在物理中的重要性 • 深入理解平面波函数的意义和价值
目录
Part
01
平面波函数的定义
Байду номын сангаас
平面波函数的数学表达式
平面波函数的数学表达式通常表示为 (f(x, y, z) = A cos(omega t - mathbf{k} cdot mathbf{r} + varphi))，其 中 (A) 是振幅，(omega) 是角频率，(mathbf{k}) 是波矢， (mathbf{r}) 是位置矢量，(varphi) 是初相。
模拟电磁波传播
在电磁学中，电磁波的传播规律也可 以通过波动方程来描述。平面波函数 可以用于模拟电磁波在真空或介质中 的传播过程，例如光波的传播。
信号处理与通信领域的应用
信号传输
在通信领域中，信号的传输通常会受到各种干扰和噪声的影响。平面波函数可 以用于信号处理中，通过对信号进行滤波、调制和解调等操作，提高信号传输 的可靠性和稳定性。
雷达与声呐
雷达和声呐是利用波的反射和传播特性进行探测和定位的技术。平面波函数可 以用于模拟雷达和声呐信号的传播过程，优化探测和定位算法，提高设备的性 能和精度。

第五章 平面波函数

第五章 平面波函数

（5.3.4）
把上式带入方程（5.3.3），得到以下的关系： （5.3.5）
把方程（5.3.2）重新整理可以得到 ： （5.3.6）
对于这个表达式，它的等相位面由下列式子给出：
（5.3.7）
它的等振幅面由下列式子给出：
（5.3.8）
根据式子（5.3.5），我们可得到下面的结论：等相位面 和等振幅面是实相互正交的。用方程表示为：
ｍ，得到场的分量表达式
（5.1011）
（具体可参考横磁波与横电波的推导公式）
其中：
。特别地， ＝0，我们有， y
-k z m Ex = ωε x 1 Ez = (k 2 - k z 2 ) m jωε Hy = - m x
（5.1.12）
这里只给出TM模的求解过程，TE模的求解与之类似。
k0 kz
kd
根据前面的讨论，当 kz k0 ，无衰减介质波导传输波的 频率趋于截止频率，这时v 0。
2 2 u = k k 我们设v＝0及 ，解特征方程可以得到： d 0
a k d 2 - k 02 ) = 0 2 a cot( k d 2 - k 02 ) = 0 2 tan(
（5.1.24）
u( x, z ) = e-jpx- jk z z
（5.3.2）
把方程（5.3.2），带入方程（5.3.1）中，得到 ：
p2 + kz 2 = k2
（5.3.3）
在通常情况下，p和 kz是复数，可以设为以下形式：
p = pr - j t k z = r - j
pr 2 - t 2 r 2 - 2 = k 2 pr t r = 0
a 2 a x2 x
a 2
根据 Ez 和 H y 在 x a 2 处需满足的条件，也就是电 场和磁场在边界处连续，即在边界处电场和磁场分别相等。 由此得到下面的方程：

波函数及其统计解释

波函数及其统计解释
5
动量分布概率（1）
设子设有平出 动 面pr现 量波 px在的ixip点波的y函pjr概y数j附z率k为近p如，zk的何则为概表(|粒r率示)(子r。？) 的|2eip动|r /量(x,，y, z那) |2么表粒示子粒具
任意粒子的波函数可以按此平面波做傅立叶展开
(r )
1
(2)3
2
( p)eipr / d 3 p
*
(
p)
p
(
p)d
3
p
p
*
(r )
pˆ
(r )d
3r
,
pˆ
力学量用算符表示
A
*
(r )
Aˆ
(r )d
3r
20
三、力学量用算符表示(5)
力学量 A 的平均值为
A
*
(r )
Aˆ
(r )d
3r
其 问中 题，：Aˆ坐为标力r学的量平A均的值算符r 。
*
(r )r
(r )d
该如何理解波函数的物理意义？为此，人们
提出了波函数的统计诠释来作为对波函数物
理意义的一种理解。
4
量子力学的基本假定之一
基本假定Ⅰ：波函数假定 微观粒子的状态可以被一个波函数完全 描述，从这个波函数可以得出体系的所 有性质。波函数一般满足连续性、有限 性和单值性三个条件。 说明：波函数一般是粒子坐标和时间的 复函数，波函数的模方代表粒子空间分 布的概率密度。
量子力学
波函数及其统计解释 粒子的动量分布 不确定度关系——进一步讨论
1
简短回顾
1、自由粒子的波函数 既然粒子具有波动性，那么就应该用一
个反映波动的函数来加以描述。 由平面波公式 Asin(kxt)

波函数几种不同形式

波函数几种不同形式
2、产生干涉的条件：
两波源具有相同的频率。
两波源具有恒定的相位差。 满足上述条件的称为相干波。 两波源的振动方向相同
两波源的波振幅相近或相等时干涉现象明显。
3、干涉加强、减弱条件：
s1
r1
p
设有两个频率相同的波源 S1S2 的振动表达式为：
y10 (s1 , t ) A10 cos(t 10 )
的变化和动能的变化“步调一致”。
3)总机械能:
E
Ek
E p
VA2 2
s in2 [ ( t
x u
)
0
]
4)能量密度:( 单位体积中的能量 )
E
V
A2
2
s in2 [ ( t
x u
)
0
]
5)平均能量密度( 在一个周期内的能量密度的平均值)
1
T
T
dt
0
1 T
T 0
A2
2
s in2 [ ( t
2 y t 2
即y1、y2 分别是它的解，则它们的任一线性组合y=C1 y1+C2 y2
也是方程的解,即上述波动方程遵从叠加原理。
实际表现：
❖ 无论是否相遇, 各列波将保持原有的特性( 频率, 波长和
振动方向等)不变, 按照原来的方向继续前进, 就象没有
遇到其他的波一样。
❖ 在其相遇区域内, 任一点处质点的的振动为各个波单独 存在时所引起的振动的矢量和。
波函数的几种不同的形式：
y( x, t )
A cos[ (t
x u
)
0
]
1 , 2
T
u
T
y( x, t )
Acos[2 ( t

波函数的几种不同的形式

波函数的几种不同的形式

1 2
u 2 A12 S1T
1 2
u 2 A22 S2T
S1 4r12 ; S2 4r22
r2
r1
A1r1 A2r2
所以球面波的振幅与离波源的距离成反比。
如果距波源单位距离的振幅为A则距波源r处的振幅为 A r
由于振动的相位沿波速方向随距离的增加而落后的关系， 与平面波类似，球面简谐波的波函数：
x) u
0
]d t
1 A22
2
A2,2
特点:
A2 2
s in2 [ ( t
x u
)
0
]
x, t
A、Ek Ep 相位,大小均相同；机械能不守恒。
( 注意与振动能量相区别 )
y
•c
y
•c
O
•B
x
• A 波形图
O•
•B
t
• A 振动图形
平衡位置（y = 0） E k 、 E p 最大。 振幅处（y = A） E k 、 E p 为 0。 B、若x 一定, E k 、 E p、E 均随 t 周期性变化。
t
u
显然能流是随时间周期性变化的。但它总为正值。
2)平均能流:在一个周期内能流的平均值称为平均能流。
P u S
3)能流密度:通过垂直于波动传播方向的单位面积的平均能流 称为能流密度或波的强度。
I P u 1 A2 2u
S
2
能流密度是单位时间内通过垂直于波速方向的单位截面的
平均能量。
I
1
A2 2u
1、平面波 在均匀不吸收能量的媒质中传播的平面波 在传播方向上振幅不变。
证明：因为
在一个周期
T内通过
S1和

平面简谐波的波函数

平面简谐波的波函数

C
B
u B
TC
2π d dC
3 ） 如图简谐波 以余弦函数表示，
求 O、a、b、c 各
点振动初相位.
(π ~ π )
t =0 A y u
t=T/4
b
Oa
c
x
A
O
O
y o π
y
a
π 2
O
y b 0
O
y
c
π 2
u
8m 5m 9m
C
BA
Dx
B
A
2π
xB
xA
2π 5 10
π
B π yB (3102 m) cos[(4π s1)t π ]
y (3102 m) cos[2π ( t x ) π ] 0.5s 10m
3）写出传播方向上点C、点D 的简谐运动方程
u
yA (3102 m) cos(4 π s1)t
Hale Waihona Puke x) u]二 波函数的物理意义
y Acos[(t x) ] Acos[2 π( t x ) ]
u
T
1 当 x 固定时， 波函数表示该点的简谐运动
方程，并给出该点与点 O 振动的相位差.
x 2 π x
u
λ
y(x,t) y(x,t T ) （波具有时间的周期性）
波线上各点的简谐运动图
2
2
比较得
T 2 s 0.8 s 2cm 200 cm u 250 cms1
2.5
0.01
T
例1 已知波动方程如下，求波长、周期和波速.
y (5cm) cosπ [(2.50s -1)t (0.01cm-1)x].
解：方法二（由各物理量的定义解之）.

平面简谐波的波函数

平面简谐波的波函数

解 确定坐标原点的 Y
振动初相0
A
由图知：t=0时， A/2
u=100m /s
x=0处的质点位于
0
1
X(
A/2处 且向位移正方向运动
-A
m)
由图知：t=0时， x=1m处的质点位于平 衡位置处且向位移负方
向运动
第十章 波动
21
物理学
第五版
0
π 3
,
2.4m,
u 100(m/s)
T /u 0.024s
在 理学
第五版
左行波的波函数：
p点的相位超前于O点相位：
所以 p点的振动方程，也就是左行波的波函数为：
第十章 波动
6
物理学
第五版
波函数的几种常用形式
第十章 波动
7
物理学
第五版
演示实验安排
周三 第3节 7班 第4节 8班
第十章 波动
8
物理学
第五版
二 波函数的物理含义
1 x一定，t变化
解
确定坐标原点的振动初相0
由：t=0时，x=0处的质点位于-A/2处 且向位移的负方向运动，知
第十章 波动
18
物第理五例版学 4.一平面简谐波，波长为12m，沿 ox轴负向传播. 图（a）所示为x=1.0m处质点的振动曲线，求波动方 程。
解：t=0时此质点的相位
0.40 0.20
5.0
t/s
t=5s时质点第一次回到平
第十章 波动
28
物理学
第五版
(1/4) 2A2
o
EP Ek
Y
WpWk x = x0
Tt
y
第十章 波动
t

得到描写自由粒子的平面波波函数： 利关系

得到描写自由粒子的平面波波函数： 利关系

2.在势场中粒子的薛定谔方程
势场中粒子的总能量
p2 E U ( x， t) 2m
则可得
i p2 U ( x， t ) t 2m
2 U ( x， t ) i 2 2m x t2Biblioteka 一维运动粒子含时薛定谔方程
上页 下页 返回 退出
d (x) dx
2
0
2 πx kπ， k 0， 1， 2， 3， a
因0<x<a/2,故得
a x 2
粒子出现的概率最大。
上页 下页 返回 退出
二、薛定谔方程
薛定谔建立的适用于低速情况的、描述微观粒子 在外力场中运动的微分方程,称为薛定谔方程。 1.自由粒子的薛定谔方程 自由粒子平面波函数方程
2 2 1 2m ( x, y, z ) U ( x, y, z ) ( x, y, z ) ( x, y, z ) E
f (t ) e

2
i Et
定态薛定谔 方程
2m
2
( E U ) 0
上页 下页 返回 退出
选择进入下一节 §13-0 教学基本要求 §13-1 热辐射 普朗克的能量子假设 §13-2 光电效应 爱因斯坦的光子理论 §13-3 康普顿效应 §13-4 氢原子光谱 玻尔的氢原子理论 §13-5 德布罗意波 微观粒子的波粒二象性 §13-6 不确定关系 §13-7 波函数及其统计诠释 薛定谔方程 §13-8 一维定态薛定谔方程的应用 §13-9 量子力学中的氢原子问题 §13-10 电子的自旋 原子的电子壳层结构
代入薛定谔方程，采用分离变量，得到
2 2 1 2m ( x, y, z ) U ( x, y, z ) ( x, y, z ) ( x, y, z )

《平面波函数》课件

《平面波函数》课件
1. "Introduction to Wave Propagation" by John S. Pringle 2. "Engineering Wave Mechanics" by William W. Morse
《平面波函数》PPT课件
本PPT课件将介绍平面波函数的定义、由来和特性，以及相关的基础知识如复 数、费马原理和傅里叶变换。还将深入讨论一维和三维平面波函数，以及球 面波函数的应用。最后总结重点回顾，并提供学习建议和参考文献。
平面波函数的定义、由来和特性
1 定义
2 由来
3 特性
平面波函数描述了在空间中 传播的波动现象。
三维平面波函数
三维平面波函数是描述沿三维空间 传播的波动。
球面波函数
球面波函数是描述从单一点源向外 传播的波动。
平面波函数的应用
物理学中的应用
平面波函数在量子力学和电磁学等物理学领域有广泛应用。
工程领域的应用
平面波函数在声学和通信工程等领域中扮演重要角色。
实际案例介绍
1
案例1
以平面波函数为基础的激光技术在医学领域中的应用。
2
案例2
使用平面波函数分析地震波的传播和地的结构。
3
案例3
以平面波函数为基础的水声通信技术在海洋学研究中的应用。
总结
1 重点回顾
平面波函数是描述在空间中传播的波动现象，具有特定的波长、频率和振幅。
2 学习建议
深入学习复数、费马原理和傅里叶变换等基础知识，以更好地理解和应用平面波函数。
3 参考文献
平面波函数的概念最早来自 波动理论的发展。
平面波函数具有波长、频率 和振幅等特性。
与平面波函数相关的基础知识

平面简谐波的波函数

平面简谐波的波函数
课堂练习 图示为 t = 1s 时的波形曲线，求波动方程。
提示 关键：求解原点o处质元初位相 o ！
(t 0)
o
2
A
y
y(m)
0.08 m/s
0.04
(t 1)
t
25
(1
0)
2
5
o
2
2
5
9
10
o
P
0.20
x (m)
t 1s
答案： y
0.04 cos [2
5
(t
x ) 0.08
9 ]
10
(
t
x u
)
o
]
(t
x u
)
o
(t
t
x
x u
)
o
x ut
y
u
☻波速即为相位传播速度 o
( 相速 ) 。
☻行波或前进波。
x
ut
·7 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
三、微分形式的平面波波动方程
对一般的平面波：
xoy系：y f (x, t) xoy系： y f (x)
y
A
cos
[
(t
x u
)
o
]
波函数亦称 波动方程 。
ut
Ao y(0 ,t )
Δt Ax
(x,t)
o
y(x,t) y
t o
·3 ·
Chapter 14. 波的传播与叠加 §14. 2 平面简谐波的波函数
波动方程 的几种标准形式： y
y
A
cos
[
(t
x u

波函数与傅里叶变换

波函数与傅里叶变换
的频率和波长为： / h 和 h / p
波矢定义为：k 2 / 所以看出自由粒子的频率和
波矢均为常量。
改写de Broglie关系为
h
p
h
e
k
2 , h / 2
14
三、自由粒子的波函数（3）
函数 描和述k都为Ac常os量(k 的 r 波应t) 该或是平 面Ae波xp[，i(k可 r用以t)下]
在经典力学中，宏观粒子在任何时刻都有完全 确定的位置、动量、能量等。然而，对于微观粒 子，其波动性远远大于宏观粒子，以致于它的某 些成对的物理量（如位置坐标和动量、时间和能 量等）不可能同时具有确定的量值。这就叫不确 定度关系或测不准原理。
下面以电子 单缝衍射为 例讨论这个 问题
多晶 铝 箔
汤姆逊（1927）：电子圆孔衍射实7 验
对于de Broglie波，有关系： k 2 / 2m
ቤተ መጻሕፍቲ ባይዱ
vg
k / m
dvg dk
m
0
根据波包说：粒子为三维空间中连续分布的一
种物质波包，波包的大小即粒子的大小。由于
dvg / dk 0 ，则波包会随着运动发生扩散，即： 粒子的大小随时间会变大。
难道电子会随着时间 “变胖”？ 22
四、一般粒子的波函数及其物理意义（7）
代入de Broglie关系得到：
k
A exp[ i
(pr
Et)]
即：自由粒子的波函数，它将粒子的波动同其能
量和动量联系了起来。它是时间和空间的函数。
15
三、自由粒子的波函数（4）
总结：由于自由粒子的能量和动量为常量，根据de
Broglie关系，其对应物质波的角频率和波矢也为常量，

平面波的归一化

平面波的归一化

平面波的归一化平面波是物理学中常用的一种模型，用于描述波动现象。

归一化是指将波函数或波动方程的解进行适当的缩放，使其满足一定的条件。

本文将介绍平面波的归一化方法和其在物理学中的应用。

首先我们来了解一下什么是平面波。

平面波是一种无限延伸的波，其波函数或波动方程解具有以下形式：ψ(x, t) = A * exp(i(kx - ωt))。

其中，ψ表示波函数，x表示位置，t表示时间，A表示振幅，k表示波矢量，ω表示角频率。

平面波的特点是在空间上是均匀的，波峰和波谷呈现平行的形态。

接下来我们讨论平面波的归一化。

归一化是一种常见的数学处理方法，它将波函数或波动方程的解进行缩放，使其满足一定的条件。

对于平面波，归一化的条件是使波函数的模的平方在整个空间上的积分等于1。

即∫ |ψ(x, t)|^2 dV = 1，其中dV表示空间的微元。

要进行归一化，我们首先需要计算平面波的模的平方。

对于平面波来说，|ψ(x, t)|^2 = |A * exp(i(kx - ωt))|^2 = |A|^2。

因此，归一化的条件可以简化为∫ |A|^2 dV = 1。

接下来我们将归一化条件应用到三维空间中的平面波中。

假设平面波在一个无限大的三维空间中传播，我们需要计算整个空间上的积分。

由于平面波在空间上是均匀的，我们可以将积分分解为三个方向上的积分：∫∫∫ |A|^2 dx dy dz = 1。

由于平面波在空间上是均匀的，波函数的模的平方在空间上是常数。

因此，我们可以将积分中的|A|^2提取出来，得到：|A|^2 ∫∫∫ dx dy dz = 1。

积分的结果应该等于1，因此∫∫∫ dx dy dz = 1 / |A|^2。

由于积分的结果是一个常数，因此我们可以将其表示为一个体积元的体积V：V = 1 / |A|^2。

由此可见，平面波的归一化常数是|A|^2的倒数，并且与空间中的体积有关。

归一化常数的平方根即为振幅A。

平面波的归一化在量子力学和电磁学等领域中有着重要的应用。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Hy = Bve-v x e-jkzz
Ez
=
-B jωε0
v2e-vxe- jkzz
Ez
=
B jωε0
v2evxe- jkzz
x<a 2
x >a x a2
2 x-a
2
根据 Ez 和 H y 在 x a 2 处需满足的条件，也就是电 场和磁场在边界处连续，即在边界处电场和磁场分别相等。
由此得到下面的方程：
（5.1.18）
该公式就是决定偶TM模的截止频率和 k z的特征方程。
▪平板介质波导的截止频率和截止波长与金属波导有一些
不同，当频率高于截止频率时，介质波导传输波是无衰
减的，这时 kz是实数。低于截止频率时，就产生衰减，
这时 k z= j 。波在传输时有衰减，就必须计算能量的
减少。由于介质波导是无损耗传输波的，那么衰减就只
选择 k0 jv 和 kd u ，使公式更简洁些。
从上面的公式可以得到分离参数方程为
u2 + kz2 = kd2 = ω2εdμd -v2 + kz2 k02 = ω2ε0μ0
（5.1.15）
把上面的分离参数方程代入公式（5.1.12）就得到方程
Ez
A u2 sin uxe jkzz
j d
H y = -Au cos uxe- jkzz
5.1平板介质波导
5.1.1标量波函数
标量波函数是矢量波函数的基础 ，矢量波动方程的直 角分量满足标量波动方程。
在介绍平板介质波导之前，先简单介绍标量波函数。 在直角坐标系中，波动方程为：
用分离变量法解上述方程。令
（5.1.1）
代入式（5.1.1）得到： 上式中的各项相互独立，分解为：
其中
为分离常数，它们满足：
能是波在传输过程中向周围辐射引起的。也就是说介质
波导可以用作天线（要求传输波的频率低于截止频率）。
无衰减模的 必须界于介质的相位常数 和空气的
常数 之间，k即z ：
kd
k0
<<
（5.1.23）
k0 kz kd
本节讨论的特征方程解是v为实数时的情况。
根频据率前趋面于的截讨止论频，率当，这k z时vk0
பைடு நூலகம்
kx
➢对于 h(kx ) = coskxx,sinkxx ：
当
k
为实数时代表纯驻波；当
x
k
为复数时代表局部驻波。
x
分别称为沿x,y,z方向的波数,用一个矢量表示
为kx , k y , kz
(5.1.8)
k = kxex kyey +kzez
于是基本波函数
（5.1.9）
φ = e e e - jkxx - jky y - jkzz
波导结构以z轴对称,图其5中.1.1a平表板示介介质波质导的厚度,.上半平面在
x=/2处,下半平面在x = -/2处。ε0 , μ0和 d , d 分别为自由
空间及介质的介电常数和磁导率。
若把问题放在二维里考虑，且设在y方向波函数无变化， 即： ＝0。波沿z方向传播，用 e-jkzz 表示波沿z方向的变 化。y •对于TM波，我们取Ａ＝ｕｘφｍ，得到场的分量表达式 如下：
可写成
（5.1.10）
▪ 电磁场矢量满足矢量波动方程，其直角分量满足标量 波动方程，可以由矢量平面波对波数的迭加得到。这一 思路不仅适用于平面波函数，也适用于其它坐标系中的 波函数；不仅适用于各向同性媒质，而且适用于各向异 性媒质。
5.1.2平板介质波导
对于各向同性介质的平板介质波导，如下图所示：
➢对于 h(k x ) = e-jkx ：
当 kx 为正实数时，代表沿＋x方向的无衰减行波；
当 kx 为实部大于零的复数时，代表沿＋x方向的衰减行波。
➢对于
：
当 为正h(实kx数) 时= ，e jk代x 表沿＋x方向的无衰减行波；
当 kx 为实部大于零的复数时，代表沿＋x方向的衰减行波。
kx ➢当 为纯虚数时，上述两波变为凋落场（急速衰减）。
同样对于x的偶函数的TM模，我们选择
e d
=
A cos uxe- jkzz
x a 2
e a
=
Be-v x e- jkz z
x a 2
（5.1.17）
它的分量参数公式依然是公式（5.1.15）。而它的场量
也由公式（5.1.12）给出。
根据 Ez 和 H y在 x a 2处的连续性条件，我们得到：
- ua cot ua = εd va 2 2 ε0 2
A u2 sin ua = -B v2e-va/2
εd
2 ε0
Au cos ua = -Bve-va/2 2
把上面的两个方程左右两边分别相除得到：
ua tan ua = εd va 2 2 ε0 2
（ 5.1.16 ）
这个公式和前面的色散关系式（5.1.15）是决定TM模
的截止频率和 k z 的特征方程。
（5.1.2） （5.1.3） （5.1.4）
式（5.1.3）中的三个公式形式相同，称为调和方程式， 它们的解称为调和函数，用 h(kx x),h(ky x),h(kz x) 表示，它 们是线性的。
φ = h(kxx)h(kyx)h(kzx)
（5.15）
上式为基本波函数。
基本波函数加权求和或求积分后，仍是波动方程的解。
（5.1011）
（具体可参考横磁波与横电波的推导公式）
其中：
。特别地，y＝0，我们有，
Ex
=
-kz ωε
m x
Ez
=
1 (k2 jωε
- kz2 )m
Hy
=
-
m x
（5.1.12）
这里只给出TM模的求解过程，TE模的求解与之类似。
另外由于平板介质波导关于x轴对称，那么得到的TM模的 解是关于x轴的奇函数或偶函数。 令 代表x的奇函数，e代表x的偶函数，则
对于有界问题， kx , k y 等取离散值，有
（5.1.6）
φ =
B(kx , ky )h(kxx)h(kyx)h(kzx)
对于有界问题，kx ky 等取连续值，有
kx , ky
φ = kx kyf(kx , ky )h(kxx)h(kyx)h(kzx)dkxdky （5.1.7）
我们详细地讨论一下平面波函数的波动特性：
在介质内的TM模的解形式为
od = A sin uxe-jkzz ,
x a 2
（5.1.13）
在空气中的TM模的解形式为
oa = Be-vxe-jkzz , oa = -Bevxe- jkzz ,
xa 2
x-a 2
（5.1.14）
这里A、B、u、v为常数，这时波在介质中是无衰减传播
的。u和v不为实数时的情况将在第三节讲述。
，无衰减介质波导传输波的 0。
我们设v＝0及 u = kd2 - k02 ，解特征方程可以得到：