下载文档原格式
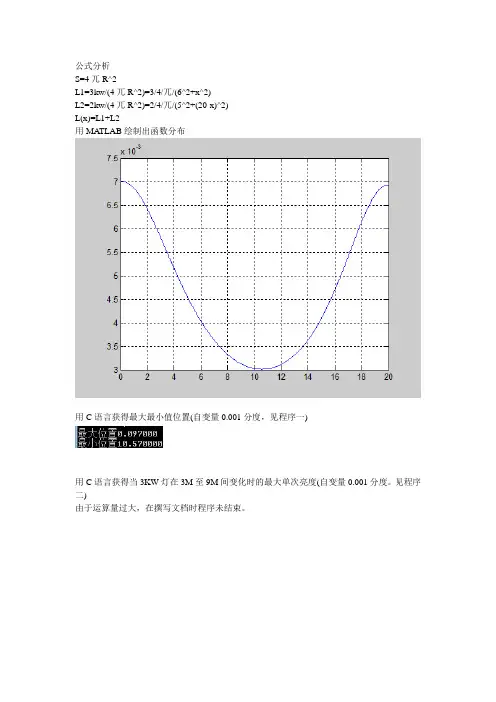
数学模型实验论文路灯安置优化问题一、摘要：现代社会，经济不断发展人民生活水平不断提高，国家采取了一系列的措施让人民生活得更舒适，而在路上安装路灯就是其中一项重要的举措。
这里我从一盏灯的照明情况的分析出发，研究怎样合理的设计路灯的度和路灯之间的间距才能满足人们的需求。
首先分析路灯照明的特性，然后建立一盏灯时面积使最大的模型及两盏灯时时路灯间距最大的模型，在此基础上建立一排路灯及两排路灯的数学模型，分析两种情况何时须灯数最少即最节约能源，其中由实际情况和生活经验来看，两排灯时交错分布照明是比较均匀的，所以在两排灯时考虑灯交错分布的情况。
关键词:照明强度、路灯设计、路灯高度、间距的优化二、问题的提出：目前大多数公共场所都安装了路灯，路灯的高度和路灯之间的间距一般是依靠经验进行设置的，并没有从优化的角度进行考虑。
在能源日益减少的今天，我们应该考虑怎样尽可能的节约能源，并且作为路段整体设计的一部分路灯的安排也直接影响到社会公共环境。
经过对我校校园内几条道路的路灯设计的观察，对校园整体室外照明有了一定的了解。
在调查时A路正在安装路灯，为获取数据的方便取该路段为研究对象。
三、背景知识：1．光强度：光源在一定范围内发出可见光辐射强弱的物理量。
以光源在某一方向上单位立体角辐射的能量来量度。
（单位：坎德拉）2．照度：单位面积上得到的光通量。
（单位：勒克司）3．通量：人眼所能感觉到的光辐射的功率。
单位时间光辐射的能 和相对视见率的乘积。
（单位：流明）4．对于眼睛最敏感的 波长的黄绿光来说，1流明相当于1/685瓦特。
一般常见或需要的照度：晴朗夏天室外背荫处得照度为1000-10000流明。
5．为保证在该路段上处处都能有满足正常活动需要的照明强度，取照度的最小值为 ，即为13700流明。
6．照度定律：点光源O 预备照明平面中心A 的距离为h 时，平面上A 点的照度。
符号规定：p 为 O 点的光强度，a 为平面的法线方向与光源到A 点的连线之间的夹角,h 为光源的高度，l 为光源到A 点的距离。
数学实验与数学建模1-2.路灯照明问题（1)解：2^/sin .r p k I α=（光照强度公式），由题意的假设两只路灯照射半径之和为20m ，可得路面上任一点的光照强度等于两路灯光照强度之和。
由题意建立如下坐标系建立方程：2^1/1sin 1.1x p k I α= 2/1)^2^2^1/(11sin x h h +=α2^2)/(2sin 2.2x s p k I -=α 2/1]^2)^(2^2/[12sin x s h h -+=α此题只考虑强度的大小，故设k=1;2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+= 要求最亮与最暗，即求I 的最大与最小值，先求I 的极值点用MA TLAB 求取clear alls=solve('(-30*x)/((25+x^2)^(5/2))+(54*(20-x))/((36+(20-x)^2)^(5/2))') s1=vpa(s,8);s1综上所述，当x=9.33m 时，为最暗点；当x=19.97m 时，为最亮点。
(2)~1. 3KW 的路灯高度在变化，此时2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+=（此时h2也为未知数）因此求偏导数3))^2)^(2^2((/2^2233)^2^2^2((/22/x s h h p x h p h I -++-=∂∂=0同理用MA TLAB 求取（2）~2. 两只路灯的高度都在变化时2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+=（此时h1，h2也都为未知数）3)^2^2^2((/2^2233)^2^2^2((/12/x h h p x h p h I ++-=∂∂=0 3))^2)^(2^2((/2^2233)^2^2^2((/22/x s h h p x h p h I -++-=∂∂=0 同理用MA TLAB 求取 2—2小型火箭初始。
2012级电子信息工程段宏坤 20121060177 1、路灯照明问题。
在一条20m宽的道路两侧，分别安装了一只2kw和一只3kw的路灯，它们离地面的高度分别为5m和6m。
在漆黑的夜晚，当两只路灯开启时，两只路灯连线的路面上最暗的点和最亮的点在哪里？如果3kw的路灯的高度可以在3m到9m之间变化，如何路面上最暗点的亮度最大？如果两只路灯的高度均可在3m到9m之间变化，结果如何？解：（1）求最亮点和最暗点一、模型假设：1、查得光强公式：I=k*(p*sinα/r2),其中，k为强度系数，p为功率，α为光线与地面的夹角，r为光源与照射点之间的距离。
2、假设两只路灯的k值相同，且均为1。
3、假设光强不受外界因素干扰。
4、如图：5、二、模型建立要求最亮点和最暗点，即求函数最大值和最小值，则求出极值点即可。
利用MATLAB求出导数为零的点，输入代码：s=solve('(-30*x)/((25+x^2)^(5/2))+(54*(20-x))/((36+(20-x)^2)^(5/2))'); s1=vpa(s,8); s1结果s1 =19.9766968.5383043+11.615790*i8.5383043-11.615790*i9.33829910.28489970e-1因为x>=0,所以复数排除综上，当x=19.97时为最亮点，x=9.34时为最暗点。
（2）如果3kw的路灯的高度可以在3m到9m之间变化，如何路面上最暗点的亮度最大？3KW的路灯的高度可以在3M到9M之间变化变化时，Q点的照度为关于x和h2的二元函数利用MATLAB求出极值点，输入solve('3/((h^2+(20-x)^2)^(3/2))-3*(3*h^2)/((h^2+(20-x)^2)^(5/2))=0')结果为：ans =20+2^(1/2)*h（舍去）20-2^(1/2)*h当x=20-2^(1/2)*h时，利用MATLAB求解h2，输入solve('-30*(20-2^(1/2)*h)/((25+(20-2^(1/2)*h)^2)^(5/2)) +9*h*(20-(20-2^(1/2)*h))/((h^2+(20-(20-2^(1/2)*h))^2)^( 5/2))=0')结果为：ans =7.422392889676861255710450993296514.120774098526835657369742179215因为 h在3~9之间，所以h2=7.42239m再利用matlab求解x和亮度I，输入h=7.42239;x=20-2^(1/2)*hI=10/((25+x^2)^(3/2))+(3*h)/((h^2+(20-x)^2)^(3/2)) 结果：x = 9.5032 I = 0.0186 可得，x=9.5032 ，h2=7.42239时，最暗点的亮度最大，为0.0186w。
21年全国数学建模竞赛c题一、题目背景与分析2021年全国数学建模竞赛C题是一道具有实际背景的数学问题。
题目描述如下：某地区计划对一批新型太阳能路灯进行试推广，为了评估其效果，需要在不同地点设置一定数量的试点。
题目要求根据路灯的照明距离、太阳能辐射强度、地形因素等条件，建立优化模型，合理布置试点，使得整个地区的照明效果最优。
二、数学模型建立1.问题抽象：可以将问题抽象为在给定条件下，求解最优的点位布置策略。
具体来说，需要建立一个关于路灯照明距离、太阳能辐射强度和地形因素的数学模型，以求解最优的试点布置方案。
2.参数设定：设路灯的照明距离为d，太阳能辐射强度为I，地形因素为T。
假设各个地点的地形因素相同，可以用一个参数表示。
3.目标函数：为了使整个地区的照明效果最优，可以建立如下的目标函数：最大化Σd^2 * I * T其中，Σ表示对所有试点的求和。
4.约束条件：根据实际情况，设置以下约束条件：1) 太阳能辐射强度I和地形因素T需满足0 <= I <= 1，0 <= T <= 1；2) 路灯的照明距离d需满足0 <= d <= 最大照明距离；3) 试点数量需满足总共设置的试点数量不超过预设数量。
三、模型求解与结果分析1.求解方法：可以使用线性规划（Linear Programming，LP）方法求解该优化问题。
线性规划是一种求解带有线性约束条件的线性目标函数最优化问题的方法。
2.求解步骤：1) 整理题目条件，列出目标函数和约束条件；2) 构建线性规划模型，输入求解器（如Excel的求解器、Python的SciPy库等）；3) 运行求解器，得到最优解。
3.结果分析：根据求解结果，分析各个地点的路灯照明距离、太阳能辐射强度和地形因素对最优试点布置方案的影响。
同时，可以对结果进行敏感性分析，探讨参数变化对最优解的影响。
四、实际应用与拓展1.实际应用：通过建立的数学模型，可以为地区路灯规划提供科学依据。
最终报告课题名称：关于城市街道路灯分布规划问题一、问题描述1.问题背景随着城市化水平的不断提高，城市街道越来越多，街道上的路灯数量也会大量增加，如何合理安放路灯便成为一个重要问题。
在能源日益紧张的今天，更需要一种能够尽可能节约能源的路灯安置方案。
2.主要问题对某一条街道两侧的路灯，在照明强度的要求已知时，寻求一种路灯安置方案，（选定合适的路灯高度、路灯之间的间距），使路灯的安置达到要求，同时路灯的数量尽可能减少，路灯的能耗达到最低。
3.问题研究的意义通过对路灯问题的研究，找到一种安置方案，优化现有路灯布局，使路灯能耗降低，以节省经济投入。
二、问题分析要使能耗最小，在路灯功率一定的情况下，只能减少路灯的使用量。
因此，在满足最低照明功率的前提下，通过改变路灯的高度来使路灯之间的距离达到最优是本问题的一个解决方案。
三、模型假设所有路灯都紧靠在路的边界线上，且照明效果都相同。
光源是点光源。
在单个光源照射下，距光源L的点的光照强度为C=f(L)；在多光源照射下，某一点的光照强度为各光源对该点光照强度的代数和。
道路处处等宽，路面上每一点的光照强度至少要达到C0。
四、说明1. 照度定律：点光源O的发光强度是P，则距点光源O为l的点的照度为E=Pℎ32. 参量变量说明：（1）设路灯的高度：ℎ，路的宽度：d=7m（2）经过实际考察，路灯的功率：P=2200W（3）路灯的间距：l（4）查阅资料可知，使物体可见的最低照明强度：c0=20W/m2五、模型建立与求解㈠单排路灯平直道路的路灯优化问题首先考虑直路上只安装一排路灯时的最优化方案，目的是通过调整路灯的高度和间距，使路灯的间距尽可能大，以减少路灯数量，节约成本。
忽略相邻的四盏路灯之外路灯对该点的影响。
建立如图坐标系，假设四盏路灯下最暗点坐标为(x,d)(x∈[0,l2])，设该点照度为E，则有E =Pℎ[ℎ2+d 2+(x −3l2)2]32+Pℎ[ℎ2+d 2+(x −l2)2]32+Pℎ[ℎ2+d 2+(x +l2)2]32+Pℎ[ℎ2+d 2+(x +3l2)2]32E ′=−2Pℎx(1[ℎ2+d 2+(x−3l2)2]52+1[ℎ2+d 2+(x−l2)2]52+1[ℎ2+d 2+(x+l2)2]52+1[ℎ2+d 2+(x+3l2)2]52)易求得当x =0时E 有最小值E m =2Pℎ[ℎ2+d 2+(3l 2)2]32+2Pℎ[ℎ2+d 2+(l2)2]32令E m =c 0，c 0=2Pℎ[ℎ2+d 2+(3l 2)2]32+2Pℎ[ℎ2+d 2+(l2)2]32用C 程序求解 程序源代码： #include <stdio.h> #include <math.h>double s(double l, double h);void main(){double c, h, t[51], delta, left, right, mid; int i; c = 20;while (1) {scanf("%lf", &h); if (h == 0) break; t[0] = 30;for (i = 1; i <= 50; i++) { t[i] = s(i, h); if ((t[i] - c) * (t[i-1] - c) <= 0)break;}left = i-1;right = i;do{mid = left * 0.618 + right * 0.382;if (s(mid, h) <= c)left = mid;elseright = mid;delta = s(left, h) - c;}while (delta <= -1);printf("l=%lf,%lf\n", left, delta);}}double s(double l, double h){double s, p, d, k1, k2;p = 2200;d = 7;k1 = h * h + d * d + l * l * 2.25;k1 = sqrt(k1 * k1 * k1);k2 = h * h + d * d + l * l * 0.25;k2 = sqrt(k2 * k2 * k2);s = 2 * p * h * (1 / k1 + 1 / k2);return s;}解得当ℎ＝9.6m时，l的值最大，l m=13.38m㈡两排路灯直路的优化问题两排路灯安置有对称和非对称两种形式，考虑美观，本方案针对对称安置优化问题进行讨论。
数学实验与数学建模路灯照明问题年级:20121060025 班级:电子信息科学与技术 学生姓名:吕佳琪 学号:20121060025云南大学信息学院路灯照明问题。
在一条20m 宽的道路两侧,分别安装了一只2kw 与一只3kw 的路灯,它们离地面的高度分别为5m 与6m 。
在漆黑的夜晚,当两只路灯开启时,两只路灯连线的路面上最暗的点与最亮的点在哪里？如果3kw 的路灯的高度可以在3m 到9m 之间变化,如何路面上最暗点的亮度最大？如果两只路灯的高度均可以在3m 到9m 之间变化,结果又如何？摘要本题利用方程(组)模型,求两只路灯连线的路面上的最暗点与最亮点。
查阅资料知:光照强度公式为2sin rp kI α=,根据题意可建立坐标轴,假设两只路灯在道路上的照射半径的长度之与为20m,可得路面上某点的照度为两只路灯在该点的照度之与。
列出方程,利用MATLAB 软件进行求解,求出该方程的最值(即最暗点与最亮点及其亮度)。
关键词:路灯照明 方程(组) MATLAB 最值 一、问题重述在一条20m 宽的道路两侧,分别安装了一只2kw 与一只3kw 的路灯,它们离地面的高度分别为5m 与6m 。
在漆黑的夜晚,当两只路灯开启时,两只路灯连线的路面上最暗的点与最亮的点在哪里？如果3kw 的路灯的高度可以在3m 到9m 之间变化,如何路面上最暗点的亮度最大？如果两只路灯的高度均可以在3m 到9m 之间变化,结果又如何？ 二、模型假设1、假设把两个路灯视为质点;2、假设忽略对路灯光照强度其她因素的影响;3、假设路灯为同一型号;4、假设路灯的光照强度2sin r p k I α=;5、假设把两只路灯连线的路面视为一条直线;6、假设两路灯在路上的照射半径长度之与为20m;7、假设路灯正常工作;三、变量说明K ………………………………路灯光照强度系数 P …………………………………路灯的功率 S ………………………………道路的宽度αi ………………………………路灯光线与地面的夹角R i………………………………路灯到路面上某点的距离h i………………………………路灯离地面的垂直距离X………………………………2KW路灯的投影到路面上某点的距离I(X)………………………………路面上某点的光照强度I i………………………………路灯光照强度四、问题分析问题一根据两路灯间的距离关系建立坐标轴,利用路灯光照强度的计算公式列出方程,再用MATLAB软件求解。
路灯的更换策略摘要本文针对路灯的更换策略中最佳更换周期的确定做了深入的研究，根据路灯更换的周期对平均费用影响的分析可知该问题是一类基于概率模型的周期性更换策略问题。
对此，本文建立了微分方程模型进行讨论求解。
首先，我们采用数理统计的思想，利用题中给出了200个抽样灯泡的寿命，借助SPSS 应用统计软件和MATLAB软件工具箱对样本进行了假设检验以及参数估计，检验结果显示，样本中的灯泡的寿命均服从均值为4002.67，标准差为96.047的正态分布。
对于问题（1），先确定了以单位时间内路政部门所花费最小为判断指标，通过计算推导得到了单位时间所花费的平均费用关于周期的表达式，即单位时间内所花的平均费用为一个周期内所花的总费用除以一个周期的小时数，周期的总费用包括灯泡成本以及罚款费用。
然后对该函数进行微分求导，在导数为0的情况下求解最佳更换周期T的表达式，经化简，得到T为最佳周期时的等式。
对于问题（2），在问题（1）以及数据处理阶段的基础上，对模型进行了求解。
采用遍历的思想，用MATLAB对周期在某一范围内进行遍历代入问题（1）中求得的关系式进行计算，当（1）中关系式成立时，输出的周期T为最佳周期，即4314小时。
对于问题（3），在问题（1）的基础上，考虑更换下来的未损坏路灯的回收价值，对模型进行修改，在从费用中减去该部分的价格，按照问题（1）的推导的思路以及问题（2）中的算法对该问题进行分析求解，最佳更换周期为3926.5小时。
最后，本文对模型中涉及的罚款费用做了敏感性分析，并结合实际做了的优缺点进行了评价，提出了离散的时间模型的改进方案，对模型进行了简单的推广。
关键词：假设检验；周期性更换策略；微分方程模型；敏感性分析一、问题的提出和重述1.1问题的提出路灯的更换和维护是路政部门的一项重要的工作，在更换路灯时间的选择上，路政部门需要考虑到跟换的成本，灯泡的寿命等众多因素。
而在更换时，花费的精力和成本主要是要专用云梯车进行线路检测和更换灯泡，向相应的管理部门提出电力使用和道路管制申请，雇用的各类人员支付的报酬等，这些工作需要的费用往往比灯泡本身的费用更高，因此，灯泡坏一个换一个的办法是不可取的。
数学模型实验论文路灯安置优化问题一、摘要：现代社会，经济不断发展人民生活水平不断提高，国家采取了一系列的措施让人民生活得更舒适，而在路上安装路灯就是其中一项重要的举措。
这里我从一盏灯的照明情况的分析出发，研究怎样合理的设计路灯的度和路灯之间的间距才能满足人们的需求。
首先分析路灯照明的特性，然后建立一盏灯时面积使最大的模型及两盏灯时时路灯间距最大的模型，在此基础上建立一排路灯及两排路灯的数学模型，分析两种情况何时须灯数最少即最节约能源，其中由实际情况和生活经验来看，两排灯时交错分布照明是比较均匀的，所以在两排灯时考虑灯交错分布的情况。
关键词:照明强度、路灯设计、路灯高度、间距的优化二、问题的提出：目前大多数公共场所都安装了路灯，路灯的高度和路灯之间的间距一般是依靠经验进行设置的，并没有从优化的角度进行考虑。
在能源日益减少的今天，我们应该考虑怎样尽可能的节约能源，并且作为路段整体设计的一部分路灯的安排也直接影响到社会公共环境。
经过对我校校园内几条道路的路灯设计的观察，对校园整体室外照明有了一定的了解。
在调查时A路正在安装路灯，为获取数据的方便取该路段为研究对象。
三、背景知识：1．光强度：光源在一定范围内发出可见光辐射强弱的物理量。
以光源在某一方向上单位立体角辐射的能量来量度。
（单位：坎德拉）2．照度：单位面积上得到的光通量。
（单位：勒克司）3．通量：人眼所能感觉到的光辐射的功率。
单位时间光辐射的能 和相对视见率的乘积。
（单位：流明）4．对于眼睛最敏感的 波长的黄绿光来说，1流明相当于1/685瓦特。
一般常见或需要的照度：晴朗夏天室外背荫处得照度为1000-10000流明。
5．为保证在该路段上处处都能有满足正常活动需要的照明强度，取照度的最小值为 ，即为13700流明。
6．照度定律：点光源O 预备照明平面中心A 的距离为h 时，平面上A 点的照度。
符号规定：p 为 O 点的光强度，a 为平面的法线方向与光源到A 点的连线之间的夹角,h 为光源的高度，l 为光源到A 点的距离。
四、模型的假设：1. 假设高度和间距的优化问题为简化模型设路灯的额定功率为定值（注：数据来源 A 路的路灯标签额定功率为220伏，额定电流为10安，所以取额定功率）。
m 7105.5-⨯2/20m w2.在考虑一排路灯的情况时，假设为完全规范的，即处处等宽。
即宽度为 5米。
（数据来源：实地测量A路的宽度）3.据相关物理知识，照明强度直接影响可见度，只有照明强度不低于某定值c。
时，才能认为物体可见。
在这里假设所有物体均匀的。
4.路长的计算：所考虑路段路的两侧均铺有花砖，所以用砖的块数乘以每块砖的边长在乘灯数减1来计算路长，经观测灯的间距大致相同，仅有少数有些差别，取平均值为64块砖。
路长：L=64*0.29*14=260米。
5.假设通过路灯的额定电压为220V，电流为10A 。
参量变量：路灯的高度 h ；路灯的功率 p ；使物体可见的最低照明强度为13700明朗；路灯的间距 l ；路的宽度 d=5米；路长 L=260米；r为灯到点A的距离；五、组建模型：一. 一盏路灯的优化问题:由物理学知识可知，被光线照射的物体的亮度依赖于它与光源之间的距离平方的倒数和光线的投射角度。
则路灯到某点A 的照明强度为 ：2322⎪⎪⎭⎫ ⎝⎛+=h r ph c（其中p 为灯的功率，h 为灯的高度，r 为灯到点A 的距离）。
地面上物体可见的区域为：02322c h r ph ≥+⎪⎪⎭⎫ ⎝⎛ 只有时0c p h ≤有解时，且2320h c ph r -≤⎪⎪⎪⎭⎫ ⎝⎛ 的区域物体可见，物体可见区域的面积为以O 为圆心，以2320h c ph -⎪⎪⎪⎭⎫ ⎝⎛ 为半径的圆，其面积为： 2r s π= = ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛-2320h c ph π 对s 关于h 求导可得04271*c p h =时，面积达最大值，可求得路灯得最优高度。
h=04271c p 其中 p=2200w ,可得最优高度h 为4.60米。
二 . 两盏路灯间距最小的的优化问题:主要考虑当高度为何值时，两灯的距离可达最小值；如图，A 点的照度在路面的各点中最小，所以l 和 h 的只需满足2322249223222412⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+++++=h d l ph h d l ph c 即可。
用求解Maple 程序如下：> fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=5},{l,h}); > fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=5.5},{l,h}); > fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=6},{l,h}); > fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=6.5},{l,h});R> fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=7},{l,h}); > fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=6.4},{l,h}); > fsolve({(1./4*l^2+25+h^2)^3=(220*h)^2,h=6.6},{l,h}); >h=6.5 时 l 最大为15. 5米三 . 一排路灯的优化问题:优化目的是确定路灯高度h 和路灯之间的距离l ，使得路灯之间的距离最大。
1.求最大路灯间距：由上图可知,路灯l 和m 之间的路段，与中点Q 相对的R 点的照明强度最小，并且计算该点照明强度时，只需考虑路灯K,L,M,N 对其的影响，其他较远的路灯对其的影响可忽略。
R 点的照明强度为：2322412161223224121692⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+++++=h d l ph h d l ph c且要使R点的物体可见应有：c≥c0其中p=2200w, d=5m, 求使得l最大的h值，具体做法：取一系列h值求使得c=的l值，比较l的大小取最大值。
用Maple求解，得h=6.6米时，l最大。
最大值为16.5米。
2．考虑边界问题可解得：x=3.5时c=20，此时x最大。
3．计算所需的总的灯数：260-3.5=256.5 256.5=15*16.5+9 因为9>3.5 所以路的另一端还需一盏灯，所需灯的总数为17盏。
四.两排路灯的优化问题:路灯的布点是否适当直接关系到照明的效果。
双侧布灯大体有两种方式：一种是对称布置，另一种是交错布置，各有优劣。
对称布置的优点是比较美观，但不足之处是照度不够均匀，适合较宽的道路。
交错布置美观上不如对称布灯，但照度比较均匀。
由于校内道路即使是干道也不很宽，如果对称布置照度不均匀的缺点会更加突出，所以事实上选择交错布置的方式更好。
由图可知，照明强度最低的点一定出现在路的中线上，且对图中AB段照明强度呈周期性变化，所以只需使AB的中点C照明强度大于等于20即可。
并且计算该点照明强度时，只需考虑路灯J,H,M,N对其的影响，其他较远的路灯对其的影响可忽略。
用Maple求解，得h= 6米时，l最大。
最大值为36.9米。
再考虑边界问题，如上面边界图所示。
A、 C两点为路的边界，设距A点最近的灯E与A的距离为x米，则J点的照明强度为：（只考虑E 和H两灯的影响）可解得：x=6 时c=20，此时x最大。
计算所需的灯数：在AE边上，AE=6米，260=6+36.9*6+32.6，所以该边需装灯7盏，且另一端剩余32.6米。
在CG边上CH=6+l/2=24.45米，260=24.45+36.9*6+13.15，所以该边装灯7盏时距另一端13.15米，13.15>6米，所以改变还需一盏灯，即总需8盏。
综上，安装两排灯时所需总数为15盏。
五 .结论：根据上述计算可知，安装两排灯时所需灯数较少，所以此种情况更能节约用电。
实际情况分析：据调查，该路段长260米，宽5米，灯高4米，间距18.56米，灯的功率2200瓦，灯共计15盏经计算照明强度最小点的值为13.04,所以照明强度过低，建议增加灯的数目。
六、结束语：大范围、复杂环境的路灯设计需考虑的因素非常多。
而我们这里只是讨论了其中的一小部分，要想精确的计算出路灯的分布是哪种最合理，还需要认真调查，认真思考，进行多次讨论，按照多方面的要求统一协调，综合考虑，要根据实际发生的情况解决具体施工问题。
校园不同的区域有不同的功能，同时环境也比较复杂。
在设计室外照照时需要考虑的方面非常多。
并且应考虑所选灯的类型，校园中一些支路上照度要求不很高，同时需要营造比较幽静的气氛，白帜灯正好满足这些要求。
七、参考文献：[1] 数理化基础知识物理（四）田均福等编山东科学技术出版社 1980 济南[2] 简明物理学词典许国宝王福山等编上海辞书出版社 1984 上海[3]数学的实践与认识第34卷第1期 2004年1月路灯安置优化问题研究高尚- 11 -。
