凸透镜成像规律的作图法

初中物理所有光路图平面镜成像凸透镜成像凹透镜成
像的作图图解急
这一类题就是“光路图”题！
有关光路图问题，主要有光的反射、光的折射、凸透镜成像规律。

考查的知识点主要有“光的反射定律”、“平面镜成像特点”、“平面镜成像原理”、“凸透镜、凹透镜中的三条特殊光线”！
需要特别注意的易错细节问题如下：
1.画法线后必须画垂直符号！
2.画光线之后必须画箭头！
3.特别注意实线与虚线！实际光线用实线，非实际光线以及辅助线用虚线！
4.光的反射图：注意利用“平面镜成像特点（物像关于镜面对称）”、“平面镜成像原理（任意两条反射光线的反向延长线相交于像点）”来画图！
期末考试必考类型题用六个光路图组合展示:。

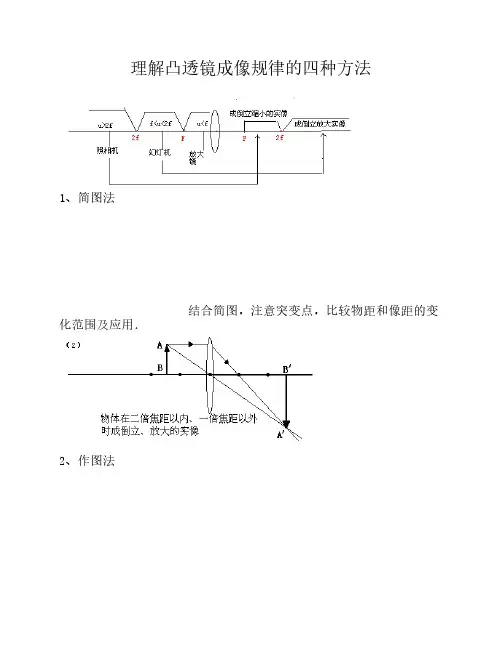
初二物理凸透镜成像规律重点难点总结一、凸透镜成像规律作图：三条特殊光线(1)与主光轴平行光线折射后过焦点(2)过光心的光线方向不变(3)过焦点的光线折射后平行于主光轴1.成实像时，像与物的位置关系：上下互换，左右互换。

这就意味着像和物的移动方向是相反的，物体向上移动，像就向下移动，物体向左移动，像就向右移动。

所以如果屏上的像在左上角，要把像移到光屏的中央，就要让像向右下移，而要让像向右下移，蜡烛就要向相反方向：左上移动即可。

成虚像时，像与物的形状一样，大小不同。

2.实像都是倒立的，与物体在透镜两侧，在主光轴两侧。

虚像都是正立的，与物体在透镜同侧，在主光轴同侧。

注意：这里面所说的倒立和正立是相对实物而言的。

3.一倍焦距处是实像与虚像的分界点，即u>f成实像；u<f成虚像；u=f不成像。

一倍焦距处是正立像与倒立像分界点，即u>f成倒立像：u<f成正立像。

4.二倍焦距处是成缩小像与放大像分界点，即u>2f成缩小的实像；u<2f成放大实像；u=f成等大的实像。

5.成实像时：u减小 v增大像变大；u增大 v减小像变小，即物近，像远，像变大。

成虚像时：u减小 v减小像变小。

总之：无论成虚像还是实像，物体离一倍焦距处越近，像越大。

6.一倍焦距处，u=f不成像。

因为光线从一倍焦距处射向凸透镜，经透镜的折射光线是平行于主光轴的，无法汇聚成一点，所以无法成像。

7.成实像时，u>f,v>f。

8.成缩小的像 v<u；成放大的像 v>u。

9.实像与虚像的相同点和不同点：相同点：都可以用眼睛看到，也都可以拍照。

不同点：实像可用光屏承接，虚像不能；实像是实际光线交点，虚像是某一点发出的光射到平面镜或凸透镜上，反射光线或折射光线反向延长线的交点。

10.物体与像运动方向相同。

11.成实像时：u>v 倒立缩小实像；u=v 倒立等大实像；u<v 倒立放大实像。

12.在实验中，如果把凸透镜遮上一部分，那么像是完整的，只是变暗；如果把烛焰遮上一部分，那么对应部分像失去。

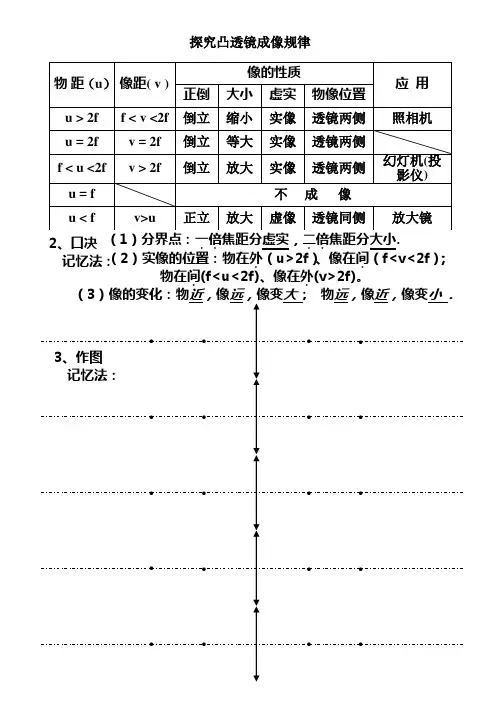
探究凸透镜成像规律4、实验：在“探究凸透镜成像规律”的实验中，从左到右依次放置蜡烛、凸透镜和光屏，首先要使它们在同一直线上，其次调整烛焰、凸透镜和光屏的高度，使它们的中心大致在同一高度，这样做的目的是烛焰的像能成在光屏中央。

5、实像：能在光屏上呈现的像，它是由实际光线相交而形成的。

虚像：不能在光屏上呈现的像，它不是由实际光线会聚而形成的，是由反射光线或折射光线反向延长线相交而形成的。

实像和虚像都能用人眼观察。

6、凸透镜成像实验中，什么情况下光屏上得不到像？①u≤f；②烛焰、凸透镜、光屏三者的中心不在同一高度7、当成实像时，如用手挡住透镜的上半部，猜一猜，光屏上的像可能有什么变化？能成完整的像，像变暗了8、什么情况下像和物体在凸透镜两侧？什么情况下像和物体在凸透镜同侧？成实像时物像异侧成虚像时物像同侧9、用凸透镜正对着太阳，发现在凸透镜的另一侧10cm处的光屏上得到一个亮点，那么将点燃的蜡烛放在位于凸透镜前15cm处时，光屏上得到的像是。

10、小明在探究凸透镜成像规律时，蜡烛与光屏分置于凸透镜两侧，保持凸透镜的位置不变，先后把蜡烛放在如图所示的a、b、c、d四点，并分别调整光屏的位置．当蜡烛位于点时，屏上出现最大的像；当蜡烛位于点时，屏上清晰的像距凸透镜最近；当蜡烛位于点时，无论怎样移动光屏，在光屏上都找不到像。

11、一个物体到凸透镜的距离是30cm时，在光屏上得到一个放大的实像，若把物体沿凸透镜的主光轴移到距凸透镜65cm处，则成像的情况是。

解析：凸透镜所成像的性质与物距有关，由第一次成倒立放大的实像可知：f<u<2f，即f<30cm<2f，解得：15cm<f<30cm，当物距为65cm，u>2f。

所以成倒立缩小的实像。

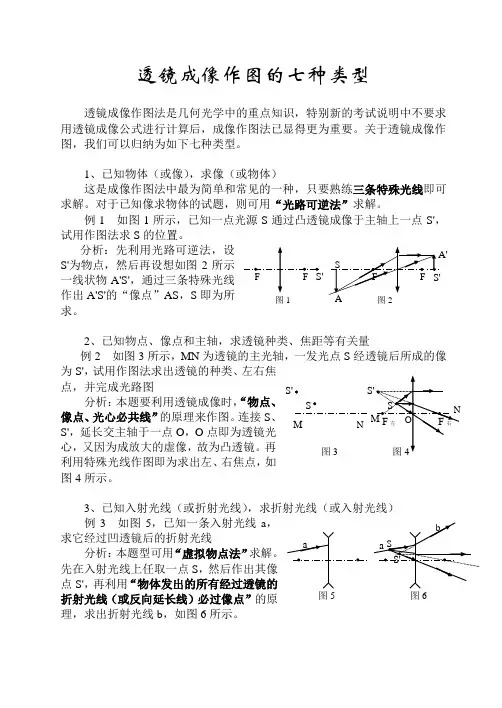
透镜成像作图的七种类型透镜成像作图法是几何光学中的重点知识，特别新的考试说明中不要求用透镜成像公式进行计算后，成像作图法已显得更为重要。

关于透镜成像作图，我们可以归纳为如下七种类型。

1、已知物体（或像），求像（或物体）这是成像作图法中最为简单和常见的一种，只要熟练三条特殊光线即可求解。

对于已知像求物体的试题，则可用“光路可逆法”求解。

例1 如图1所示，已知一点光源S 通过凸透镜成像于主轴上一点S'，试用作图法求S 的位置。

分析：先利用光路可逆法，设S'为物点，然后再设想如图2所示一线状物A'S'，通过三条特殊光线作出A'S'的“像点”AS ，S 即为所求。

2、已知物点、像点和主轴，求透镜种类、焦距等有关量例2 如图3所示，MN 为透镜的主光轴，一发光点S 经透镜后所成的像为S'，试用作图法求出透镜的种类、左右焦点，并完成光路图 分析：本题要利用透镜成像时，“物点、像点、光心必共线”的原理来作图。

连接S 、S'，延长交主轴于一点O ，O 点即为透镜光心，又因为成放大的虚像，故为凸透镜。

再利用特殊光线作图即为求出左、右焦点，如图4所示。

3、已知入射光线（或折射光线），求折射光线（或入射光线） 例3 如图5，已知一条入射光线a ，求它经过凹透镜后的折射光线 分析：本题型可用“虚拟物点法”求解。

先在入射光线上任取一点S ，然后作出其像点S'，再利用“物体发出的所有经过透镜的折射光线（或反向延长线）必过像点”的原理，求出折射光线b ，如图6所示。

图1图5图6S S'图3 M N4 、已知入射光线和折射光线，求解透镜种类及有关量例4 如图7所示，已知一条入射光线a 和它经过透镜后的折射光线b ，试用作图法求出透镜类别及左右焦点分析：由题可知，因光线经透镜后发散，故为凹透镜，然后用“虚拟物点法”可求解。

本题采用了“焦平面法”作图。

凸透镜成像规律一、凸透镜成像规律凸透镜成像规律口决记忆法口决：“一焦分虚实，二焦分大小；虚像同侧正；实像异侧倒，物远像变小”u是物距 v是像距 f是焦距物距像距像的大小像的正倒和虚实应用例子u>2f f<v<2f 缩小倒立的实像照相机u=2f v=2f 等大倒立的实像测焦距f<u<2f v>2f 放大倒立的实像幻灯机投影仪u=f 不成像（呈平行光射出）！！粗略测焦距u<f v>u 放大正立的虚像放大镜①当u=f时，_________________________________________②当u=2f时，__________________________________________③实像、虚像分界点：____________________________________④放大、缩小实像分界点：__________________________________1、为了使幕上的像“正立”（朝上），幻灯片要倒着插。

2、照相机的镜头相当于一个凸透镜，暗箱中的胶片相当于光屏，我们调节调焦环，并非调焦距，而是调镜头到胶片的距离，物离镜头越远，胶片就应靠近镜头。

3、（1）眼睛（相当于）：晶状体（相当于）（相当于底片）瞳孔（相当于）（改变晶状体的薄厚）成像特征：像。

（2）近视眼的成因：晶状体太，折光能力太，光会聚在视网膜。

近视眼的矫治：佩戴。

（3）远视眼的成因：晶状体太，折光能力太，光会聚在视网膜。

远视眼的矫治：佩戴。

二、显微镜的工作原理1.显微镜的结构（1）目镜：靠近眼睛的凸透镜（2）物镜：靠近被观察物体的凸透镜叫物镜目镜物镜被观察的物体AB在物镜的________________________之间,成的像A’B’在物镜的_________以外,成的是一个_____,_______的____像.1）来自观察物体的光经过物镜后成一个_____的____像.物镜所成的像A’B’在目镜的_____________内,目镜相当于是一个_________,把实像A’B’放大.实像A’B’通过目镜成的像A’’B’’是相对与A’B’_______,_______的___像.’ A’目镜物镜 B’ A’A B B’’ A’’2）目镜的作用则像一个普通的放大镜,把这个像再________.3）经过2次放大作用,物体经过显微镜成的是_______,________的像.2.望远镜望远镜的结构（1）目镜：靠近眼睛的凸透镜（2）物镜：靠近被观察物体的凸透镜叫物镜物镜目镜目镜1）望远镜的工作原理被观察的物体AB到物镜的距离远大于物镜的__________,成的像A’B’在物镜的________________________之间,成的像A’B’是_______,_______的_____像.A物镜B B’A’物镜成像图2）物镜的作用是使远处的物体在焦点附近成__ ___像.B’’B’目镜A’’ A’目镜成像图物镜所成的像A’B’在目镜的___________内,目镜的作用相当于一个_________,把实像A’B’放大.实像A’B’通过目镜成的像A’’B’’是相对于A’B’_______,________的_____像. 3）目镜的作用相当于放大镜,把这个像_______.4）远处的物体经过望远镜成的是________,_________的像.但是我们在用望远镜观察时,会感觉物体被_________了.我们有时看远处的汽车,感觉比身边的课本还小,但是我们知道汽车比课本要大的多.那么眼睛感觉物体的大小取决于什么呢?.科学家研究发现,眼睛感觉物体的大小与眼睛观察物体的_______有关.看近处的人视角大,感觉人就比较大看远处的人视角小,感觉人就比较小视角的大小除了与物体自身的_______有关外,还与物体到眼睛的________有关,所以眼睛感觉物体的大小与物体本身的_______和距离物体的_______都有关系.例1．一个物体到凸透镜的距离为30 cm时，在光屏上得到一个放大的实像，若把物体沿凸透镜主轴移动到距凸透镜45 cm处，则成像的情况一定是（）A．放大的实像 B．等大的实像 C．缩小的实像 D．上述三种情况都可能例2．在做凸透镜成像实验时，当蜡烛距凸透镜15 cm，在光屏上成放大的像，则下列说法中不正确的是（）A．蜡烛距透镜40 cm时，一定成缩小的实像B．蜡烛距透镜18 cm时，可能成放大的实像C．蜡烛距透镜20 cm时，一定成放大的实像D．蜡烛距透镜6 cm 时，一定成放大的虚像实战演练的距离的,当拍摄近的景物时,镜头往,离胶片一些,因而在胶片上成的像一些2．如图所示是简易天文望远镜的内部结构。

凸透镜成像规律八种记忆方法一、作图成像法光学作图，是掌握光学内容的有效途径之一。

因此，凸透镜成像规律完全可以利用三条特殊光线中的两条，而找到像点，这种方法适用于基础较好的学生，也可以作为实验后，强化知识的一种补充，也可以为那些要参加各种物理竞赛的学生，作为知识的一种拓宽。

方法是过物体上的一点，画出三条特殊光线中的任意两条，然后找到光线通过凸透镜后相交的点，或者光线的反向延长线的交点，就是物体上该点的像点。

再根据物体与主光轴的垂直关系，画出像也与主光轴垂直，就可以画出虚实像。

还可以借此介绍虚实像。

本文列举两种利用作图法探究成像规律，作图在下：两条光线：(1)过光心的光线方向不变；(2)平行于主光轴光线通过焦点。

(1)u ＞2f ，f ＜v ＜2f ，成倒立、缩小的实像由实际光线会聚形成的像叫实像．．(2)u ＜f ，v ＞u ，成正立、放大的虚像由光线反向延长线会聚形成的像叫虚像．． 这种方法适合学习能力较好的学生，初二学生接受起来可能有些困难，可以在初三第一轮复习时，帮助学生记忆，减轻复习时的学生的记忆压力。

二、光路可逆法光路可逆性是光学的一个重要知识点，学生对这个知识也是记忆犹新。

具体方法是先根据作图法作出一种成像规律的图后，提醒学生从光路可逆性来考虑问题，把作出来的图，从反面看一下，又是什么成像规律？这样所有的成像规律，就可以从光路可逆性来记住规律。

下图中就是利用光路可逆性，完成两个成像规律！(1)u ＞2f ，f ＜v ＜2f ，倒立、缩小的实像 (2)f ＜u ＜2f ，u ＞2f ，倒立、放大的实像这种方法理解层次较高，学生理解起来也很难，可以作为新课以后的辅助练习。

三、童话故事记忆法一个天气晴朗、阳光明媚的冬天，唐僧师徒一行四人，为取真经，他们继续向西方徒步前行。

他们来到一个山洞中休息吃饭。

山洞前有一个大的冰山，冰山中间厚、边缘薄。

孙悟空到外面弄了一些吃的回到山洞前，他看到冰山后面的山洞里，也有一只倒立、缩小的孙悟空，他以为是妖精，又来吃唐僧的肉了，连忙拿出金箍棒，准备降服妖精。

凸面镜成像平行光线投射到凸面镜上，反射的光线将成为散开光线，如果顺着反射光线的相反方向延伸到凸面镜镜面的后面，可会聚并相交于一点，这一点就是凸面镜的主焦点（F），属虚性焦点凸面镜成像的几何作图原则与凹面镜相同，也就是：·从物体的某一点（A）作一与主轴平行的直线为入射光线，入射光线到达球面镜镜面时，发生反射，反射后的方向相反的直线为反射光线，此反射光线必然通过主焦点（F）。

·从物体的同一点（A）通过镜面的曲率中心（C）的连线为副轴，此副轴与上述通过主焦点的反射光线发生相交的点（A′），即为该物体成像之处，凸透镜成像规律物体放在焦点之外，在凸透镜另一侧成倒立的实像，实像有缩小、等大、放大三种。

物距越小，像距越大，实像越大。

物体放在焦点之内，在凸透镜同一侧成正立放大的虚像。

物距越小，像距越小，虚像越小。

在光学中，由实际光线汇聚成的像，称为实像；反之，则称为虚像。

有经验的物理老师，在讲述实像和虚像的区别时，往往会提到这样一种区分方法：“实像都是倒立的，而虚像都是正立的。

”所谓“正立”和“倒立”，当然是相对于原像而言。

平面镜、凸面镜和凹透镜所成的三种虚像，都是正立的；而凹面镜和凸透镜所成的实像，以及小孔成像中所成的实像，无一例外都是倒立的。

当然，凹面镜和凸透镜也可以成虚像，而它们所成的两种虚像，同样是正立的状态。

那么人类的眼睛所成的像，是实像还是虚像呢？我们知道，人眼的结构相当于一个凸透镜，那么外界物体在视网膜上所成的像，一定是实像。

根据上面的经验规律，视网膜上的物像似乎应该是倒立的。

可是我们平常看见的任何物体，明明是正立的啊？这个与“经验规律”发生冲突的问题，实际上涉及到大脑皮层的调整作用以及生活经验的影响。

当物体与凸透镜的距离大于透镜的焦距时，物体成倒立的像，当物体从较远处向透镜靠近时，像逐渐变大，像到透镜的距离也逐渐变大；当物体与透镜的距离小于焦距时，物体成放大的像，这个像不是实际折射光线的会聚点，而是它们的反向延长线的交点，用光屏接收不到，是虚像。