第03讲 三角形与角平分线

三角形中角平分线的定义三角形，这个我们在小学数学课上学过的形状，真的是个奇妙的东西。

三条边，三个角，听起来简单，但里面的奥妙可不少。

今天咱们就聊聊三角形中的角平分线，哎呀，这个名字一听就有点复杂，对吧？别担心，我来给你捋一捋，让你一下子明白过来。

角平分线顾名思义，它就是把一个角给分成两个相等的角。

这就像是把一块蛋糕切成两份，虽然都一样大，但你觉得两边的味道是一样的吗？哈哈，可能不会，因为每个人都有自己喜欢的那一块。

但在数学里，这两个角可就是一模一样的，完全不差分毫。

这条线从角的顶点出发，直直地延伸到对面的边上，像个英勇的骑士，一路披荆斩棘。

你可能会问，这个角平分线有什么用呢？角平分线在我们生活中也有不少应用。

比如说，建筑设计、工程测量，甚至是打理花园，都是需要用到这种神奇的线的。

想象一下，设计师在画图纸时，心里默念：“要把这个角平分，才能确保这个房子建得又稳又美！”是不是听起来很酷？三角形的角平分线有个很棒的性质：它把对面的边分成的两段，和它的两个角的比值是相等的。

简单说，就是边上的两段长度和相应的角大小是有关系的。

就像是你和朋友去吃饭，最后你们各自点了多少菜，大家心里都有数，绝对不想让对方多点或少点，这样才公平嘛，对吧？讲到这里，可能有人会觉得这些性质有点抽象。

别着急，咱们用个例子来说明一下。

想象你有个三角形ABC，角A的角平分线穿过对面的边BC，交点叫D。

你会发现，BD 和DC的长度比就是角A的大小与角B的大小的比。

这可是个绝对的真理，听起来是不是有点像魔法？这种规律性让我们对三角形的理解更深入，也让我们在解题时有了更多的工具。

你看，虽然数学有时让人觉得枯燥无味，但只要好好去了解，就会发现里面的乐趣。

就像在翻一本书，你不知道书里有多精彩，直到你真正打开它的一页。

角平分线就是这样一种神奇的存在，它在三角形里默默无闻，却又扮演着极其重要的角色。

生活中也处处有它的影子，只是我们常常没注意到而已。

角平分线不仅是数学中的一个概念，更是让我们在生活中找到平衡与和谐的小秘密。

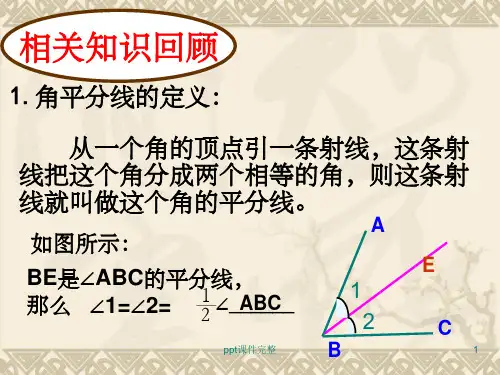
三角形中的角平分线和中线性质一、角平分线性质1.定义：从三角形一个顶点出发，将这个顶点的角平分成两个相等的角的线段，称为这个角的角平分线。

（1）一个角有且只有一条角平分线。

（2）角平分线上的点到这个角的两边的距离相等。

（3）角平分线与这个角的对边相交，交点将对边分为两条线段，这两条线段的长度相等。

二、中线性质1.定义：连接三角形一个顶点与对边中点的线段，称为这个顶点的中线。

（1）一个三角形有且只有三条中线。

（2）中线的长度是该顶点与对边中点距离的一半。

（3）中线平行于第三边，并且等于第三边的一半。

（4）三角形的中线将第三边平分成两条相等的线段。

三、角平分线与中线的交点性质1.定义：三角形的三条角平分线与三条中线的交点，称为三角形的心。

（1）三角形的心是三角形内部的一个点。

（2）三角形的心到三角形的三个顶点的距离相等。

（3）三角形的心到三角形的任意一边的距离相等。

四、角平分线和中线的应用1.判断三角形的形状：（1）如果一个三角形的三条角平分线相等，那么这个三角形是等边三角形。

（2）如果一个三角形的三条中线相等，那么这个三角形是等腰三角形。

2.求解三角形的问题：（1）利用角平分线求解三角形的角度。

（2）利用中线求解三角形的边长。

三角形中的角平分线和中线性质是解决三角形相关问题的重要知识点。

掌握这些性质，可以帮助我们更好地理解和解决三角形的相关问题。

习题及方法：1.习题：在三角形ABC中，角A的角平分线与中线交于点D，若AD=3，BD=4，求AB的长度。

答案：由于点D是角A的角平分线与中线的交点，根据性质可知AD=BD。

又因为AD=3，BD=4，所以AB=5。

2.习题：在等边三角形EFG中，求证：每条角平分线也是中线。

答案：由于三角形EFG是等边三角形，每个角都是60度。

根据角平分线性质，每条角平分线将角平分成两个30度的角。

又因为等边三角形的中线也是角平分线，所以每条角平分线也是中线。

3.习题：在三角形APQ中，若角APQ的角平分线与中线交于点M，且AM=4，PM=6，求AB的长度。

三角形的角平分线定义和应用嘿，朋友们！今天咱来唠唠三角形的角平分线。

你说这角平分线啊，就像是三角形这个大家庭里的和事佬。

你看啊，三角形有三个角，这角平分线呢，就不偏不倚地把每个角都分成了相等的两部分。

就好像你有一块蛋糕，要平均分给两个人，那中间切的那一刀就是角平分线啦！它把一个角分成了同样大小的两份，多神奇呀！角平分线在数学里的用处可大了去了。

它就像一把钥匙，能帮我们打开很多难题的大门。

比如说，知道了角平分线，我们就能知道很多关于角的信息，这对我们解决问题可太有帮助啦。

咱举个例子哈，就好比你要去一个陌生的地方，角平分线就是给你指引方向的那个标志。

有了它，你就能更清楚该往哪儿走，不至于迷路呀。

而且啊，角平分线还和很多其他的知识点有关系呢。

它和三角形的中线、高线啥的，都能一起合作，共同解决问题。

这就像是一个团队，大家各有所长，互相配合，就能把事情干得漂漂亮亮的。

你想想，要是没有角平分线，那数学世界得少了多少乐趣和挑战呀！它就像生活中的那些小惊喜，总是在不经意间给我们带来惊喜。

角平分线还能让我们看到数学的美妙之处。

它那简洁明了的定义，却蕴含着无穷的奥秘。

这就好像一首好听的歌曲，虽然歌词简单，但是却能打动人心。

咱再说说它在实际生活中的应用吧。

虽然不像买东西、算钱那么直接，但是它的原理可是无处不在的哟！比如说设计一个东西的形状啦，或者规划一个场地的布局啦，都可能用到角平分线的知识呢。

哎呀呀，说了这么多，角平分线是不是很有意思呀？它虽然看起来不起眼，但是在数学的世界里，可是有着举足轻重的地位呢！所以啊，咱可不能小瞧了它，得好好去研究研究，说不定就能发现更多有趣的东西呢！这就是三角形的角平分线，一个小小的概念，却有着大大的作用！你说是不是呀？。

三角形的角平分线引言三角形是几何学中最基本的图形之一，它由三条边和三个顶点组成。

在三角形中，角平分线是指从一个角的顶点出发，将该角分为两个相等的角的线段。

本文将介绍三角形的角平分线的性质和相关定理。

角平分线的定义在三角形ABC中，假设角A的顶点是顶点A，其角平分线是指从顶点A出发，将角A分为两个相等的角。

角平分线的性质在三角形ABC中，角平分线有以下性质：1.角平分线将角分为两个相等的角。

证明：假设角A的角平分线为AD，可以通过角A的两边与角平分线的交点D分别连接线段CD和BD，得到三个小三角形ACD、BCD和ABD。

根据直角三角形的性质，我们知道ACD ≌ BCD 和ABD ≌ BCD，因此角ACD和角ABD是相等的。

2.角平分线上的点到三角形的两边距离相等。

证明：假设角A的角平分线为AD，可以通过点D分别作垂线DE和DF分别与边AC和边BC相交。

根据直角三角形的性质，我们可以得知三角形AED ≌三角形BED和三角形AFD ≌ 三角形BFD。

因此，DE = DF。

3.三角形的三条角平分线交于一点。

证明：假设角A的角平分线为AD，角B的角平分线为BE，角C的角平分线为CF。

我们可以通过两条角平分线相交的性质，得到∠CAD = ∠BAD 和∠BAE =∠CAE。

由于∠CAD = ∠BAE，所以角DAB = ∠CAB。

同理，可以证明角BAC = ∠BAC。

因此，三个角平分线交于点D。

角平分线的相关定理角平分线定理在三角形ABC中，角A的角平分线和边BC的关系为：angle_bisector_theoremangle_bisector_theorem其中，BD为角平分线，根据角平分线的性质可得：AB/AC = BD/CD。

角平分线的外角定理在三角形ABC中，如果角平分线BD将边AC分成了线段AE和EC，那么∠BAD = ∠BCE。

角平分线的内角定理在三角形ABC中，如果角平分线BD将角BAC分成了角BAD和角CAD，那么∠BAD = ∠CAD。

三角形中的角平分线三角形是中学数学中常见的一个几何图形，它由三条线段组成，每条线段连接两个角，并形成三个角。

在三角形中，角平分线是指从一个角的顶点出发，将该角分成两个相等的角，并与对边相交的线段。

角的平分线在三角形中具有重要的几何性质和应用。

本文将详细介绍三角形中角平分线的特点和应用。

一、定义角平分线是指从一个角的顶点出发，将该角分成两个相等的角，并与对边相交的线段。

对于任意三角形ABC，若AD为角BAC的角平分线，则∠BAD≅∠CAD。

二、三角形角平分线的性质1. 角平分线将角分成两个相等的角。

若AD为角BAC的角平分线，则∠BAD≅∠CAD。

2. 角平分线与对边相交于三角形的内心。

三角形的内心是角平分线三条的交点，记为I。

即角平分线BE、CF和AD的交点为内心I。

3. 角平分线与对边的比例关系。

根据内切角的性质，有以下比例关系：AB/AC = BD/DC = c/bBC/BA = CE/EA = a/cCA/CB = AF/FB = b/a4. 角平分线长度的性质。

设角BAC的角平分线AD与对边BC相交于点D，则有以下关系： BD/DC = AB/AC (根据角平分线与对边的比例关系)AD/DC = AB/BC (根据角平分线定理)根据以上性质，可以推导出角平分线长度的计算公式。

三、三角形角平分线的应用1. 寻找三角形的内心。

通过求解角平分线的交点，可以确定三角形的内心。

内心是三角形的一个重要特征点，在几何学和三角学中有广泛的应用。

2. 解决三角形的相关问题。

通过应用角平分线的性质，可以解决各种与角平分线相关的三角形问题，如角平分线的长度、角平分线与周长的关系等。

这些问题是解决几何学和三角学中经典问题的重要方法之一。

3. 构造等分角。

如果需要将某个角等分为多个角，可以通过绘制角平分线来实现。

通过绘制角平分线，可以将原角等分为任意个相等的角。

四、结语三角形中的角平分线在数学中具有重要的地位和应用。

三角形的角平分线几何语言三角形的角平分线是指从三角形的一个顶点出发，将相邻两边的夹角平分成两个相等的角的线段。

角平分线在几何学中有着重要的应用和性质。

我们来看一下角平分线的定义。

对于三角形ABC来说，如果从顶点A出发，将∠BAC的角平分成两个相等的角∠BAD和∠DAC，则线段AD称为角BAC的角平分线。

角平分线有一些重要的性质。

首先，角平分线上的点到三角形的两边的距离相等。

也就是说，如果点D是角BAC的角平分线上的一点，那么AD=BD=CD。

这个性质可以通过角平分线的定义和角的性质来进行证明。

角平分线将对边分成一定比例。

具体来说，如果有一个三角形ABC，角平分线AD将∠BAC的角平分成两个相等的角∠BAD和∠DAC，那么有AD/DB=AC/BC。

这个性质可以通过相似三角形的性质来进行证明。

接下来，我们来探讨一下角平分线的一些应用。

首先，角平分线可以帮助我们求解三角形的各个角的大小。

如果我们已知一个三角形的两边的长度和它们夹角的大小，我们可以通过角平分线的性质来求解出三角形其他两个角的大小。

角平分线还可以帮助我们求解三角形的边的长度。

如果我们已知一个三角形的两个角的大小和它们对应的两边的长度，我们可以通过角平分线的性质来求解出第三边的长度。

这个方法被称为角平分线定理。

角平分线还有一些重要的性质。

例如，如果一个点在一个三角形的角平分线上，那么这个点到三角形的三个顶点的距离之比等于这个点到三角形的三个对边的距离之比。

这个性质被称为角平分线定理的逆定理。

角平分线还有一些其他的性质和定理，例如外角平分线、内接角平分线、垂直平分线等。

这些性质和定理在几何学的证明和计算中有着重要的应用。

总结起来，三角形的角平分线是从一个顶点出发，将相邻两边的夹角平分成两个相等的角的线段。

角平分线具有一些重要的性质，包括角平分线上的点到三角形的两边的距离相等，角平分线将对边分成一定比例等。

角平分线在几何学中有着重要的应用，可以帮助我们求解三角形的角的大小和边的长度。

三角形的角平分线角平分线是指从一个三角形的顶点出发，将该角分成两个相等的角的线段。

在三角形中，每个角都有三条平分线，它们相交于一个点，称为内心。

角平分线的性质有很多，下面我们来逐一介绍。

1. 内心：三角形的角平分线相交于一个点，这个点被称为三角形的内心。

内心到三角形的三条边的距离相等，这个距离被称为内心到三边的距离，也是内心半径。

2. 角平分线长度：三角形的角平分线将对边分成两个段，这两个段的长度与角平分线所在边的长度的比相等。

也就是说，如果一条角平分线将对边分成长度为a和b的两段，那么 a:b等于边所占对边的比。

3. 角平分线的垂直性：三角形的角平分线与对边垂直。

即在一个三角形ABC中，角A的平分线与边BC垂直，角B的平分线与边AC垂直，角C的平分线与边AB垂直。

4. 角平分线的外角平分性：三角形的外角是指一个三角形内部的一个角的补角。

角平分线同时也是外角的平分线，也就是说，如果一条角平分线平分了某个外角，那么这个外角被平分成两个相等的角。

5. 角平分线的交点：三角形的三条角平分线相交于一个点，称为内心。

内心是三角形内心圆的圆心，内心到三角形的三条边的距离相等，即内心到三边的距离相等。

此外，内心到三角形三个顶点的距离相等，即内心到顶点的距离也是相等的。

角平分线在三角形的研究中具有广泛的应用。

它不仅可以用于求解三角形的各个参数，还可以应用到三角形的几何性质证明中。

最后，角平分线也是解决三角形相关题目中的一个有效的思路和方法。

通过运用角平分线的性质，可以使问题的求解更加简单和方便。

总结起来，角平分线是一个具有重要性质的几何概念，它不仅能够划分和研究三角形内部的角度，还可以应用到解决三角形问题的过程中。

对于了解三角形的角平分线性质以及灵活运用角平分线的方法，对于解决相关问题和提升几何推理能力都具有重要作用。

第3讲三角形与角平分线知识导航1.三角形内外角平分线夹角模型；2.其它常见角平分线夹角模型.【板块一】三角形内外角平分线的夹角的三个基本模型方法技巧角平分线性质＋三角形内角和定理＋三角形外角性质＋整体思想、化归思想＋设参数计算模型 模型一三角形两内角平分线夹角【例1】如图，点P 是△ABC 两条内角平分线的交点，求证:∠P ＝90°＋12∠A. PCBA【例2】已知在△ABC 中，∠A ＝60°.(1)如图1，∠ABC ，∠ACB 的角平分线交于点O ，求∠BOC 的度数；(2)如图2，∠ABC ，∠ACB 的三等分线交于点O 1，O 2，则∠BO 1C ＝__，∠BO 2C ＝_____； (3)如图3，∠ABC ，∠ACB 的n 等分线交于点O 1，O 2，……O n －1. 则∠BO 1C ＝_______，∠BO n －1C ＝__________.(用含n 的代数式)图1图2图3O 2O 1A CA BCO模型二三角形两外角平分线夹角【例3】如图，点P 是△ABC 两条外角平分线的交点，求证:∠P ＝90°－12∠A. ABCDE模型三三角形一内角平分线与一外角平分线的夹角【例4】如图，点D是BC延长线上一点，PB平分∠ABC，PC平分∠AC D.求证:∠P＝12∠A.AB C DE针对练习11.如图，在△ABC中，∠A＝60°，BP，BE把∠ABC三等分，线段CP，CE把∠ACB三等分，求∠BPE的度数.PACE2.如图，在平面直角坐标系中，点A为x轴上的一点，点B为y轴上的一点，AC平分∠BAx，BC平分∠ABy，求∠C的度数.3.如图，在平面直角坐标系中，点A为x轴上的一点，点B为y轴上的一点，AD平分∠BAx，BP平分∠OBA，BP与DA的延长线交于点P，求∠P的度数.【板块二】与三角形有关的其它角平分线模型 ◆方法技巧◆角平分长性质＋三角形内角和定理十三角形外角性质＋整体思想，化归思想＋设参数计算 模型四◆角平分线＋高线夹角模型(设参计算＋整体思想)【例5】(1)已知△ABC 中，∠B ＞∠C ，AD ⊥BC 于D ，AE 平分∠BAC ，如图1，设∠B ＝x ，∠C ＝y ，试用x ，y 表示∠DAE ，并说明理由；(2)在图2中，其他条件不变，若把“AD ⊥BC 于D ”改为“F 是AE 上一点，FD ⊥BC 于D "，试用x ，y 表示∠DFE ＝_________；(3)在图3中，若把(2)中的“点F 在AE 上”改为“点F 是AE 延长线上一点”，其余条件不变，试用x ，y 表示∠DFE ＝_______；(4)在图3中，分别作出∠BAE 和∠EDF 的角平分线，交于点P ，如图4，试用x ，y 表示∠P ＝_____.图4图1图2图3PF DBE AFDBE CEBD AABCDEF模型五燕尾形双角平分(设参计算＋整体思想)【例6】如图，BP ，CP 分别平分∠ABD ，∠ACD ，它们交于点P .求证:∠P ＝12(∠A ＋∠D ). P DCBA模型六蝶形(8字形)双角平分(设参计算＋整体思想)【例7】(1)模型:如图1，AD ，BC 交于O 点.求证:∠D ＋∠C ＝∠A ＋∠B. (2)模型应用:如图2，∠BAD 和∠BCD 的平分线交于点E . ①若∠D ＝30°，∠B ＝40°，则∠E 的度数是______；②直接写出∠E 与∠D ，∠B 之间的数量关系是:__________；(3)类比应用:如图3，∠BAD 的平分线AE 与∠BCD 的平分线CE 交于点E .若∠D ＝m °，∠B ＝n °，(m ＜n ).求∠E 的度数.(用含有m ，n 的式子表示)图1图2图3EABCDBCDOEDC A针对练习21.如图，∠ABD ，∠ACD 的角平分线交于点P ，若∠P ＝20°，∠D ＝10°，求∠A 的度数.ABCDP2.如图，∠ABD 的平分线与∠ACD 的邻补角∠ACE 的平分线所在的直线交于点I . (1)写出∠I 与∠A ，∠D 之间的数量关系式并证明；(2)直接写出∠I 与∠A ，∠D 之间的数量关系式为___________.图1图2I ABDCE AB CD EI。

三角形内外角平分线与角的关系咱来说说三角形内外角平分线和角的那些事儿。

一、内角平分线与角的关系。

1. 一个内角平分线把这个角分成两个相等的角。

- 你看啊，在三角形里，假如有个角∠A，它的角平分线AD一出来，那就把∠A 分成了两个小角，∠BAD和∠CAD，这俩小角那可是一模一样大的。

就好像把一块蛋糕（∠A这个角），从中间（角平分线）平均切成了两块（∠BAD和∠CAD）。

2. 三角形内角平分线定理。

- 这个定理可有点意思呢。

如果AD是△ABC中∠A的平分线，它交BC于D点，那么就有AB/AC = BD/DC。

你可以想象成，角平分线AD就像一个裁判，它把BC边分成的两段BD和DC的比例，就和AB、AC这两条边的比例是一样的。

这就好像是三角形里的一种“平衡规则”，角平分线在这儿起着一种特殊的协调边和角关系的作用。

二、外角平分线与角的关系。

1. 外角平分线与相邻内角的关系。

- 三角形一个角的外角平分线和它相邻的内角是互补的关系。

比如说，在△ABC 中，∠A的外角∠CAE，它的平分线AF，那∠CAF和∠BAF把∠CAE平分了。

而∠CAE和∠BAC是互补的，也就是∠CAE+∠BAC = 180°。

这就好比一个在外面（外角），一个在里面（相邻内角），它们合起来就是一条直线的角度。

2. 三角形外角平分线定理。

- 如果AE是△ABC的外角∠CAE的平分线，交BC的延长线于E点，那么有AB/AC=BE/CE。

这就和内角平分线定理有点类似啦，外角平分线也在协调着边和角之间的比例关系。

只不过这里是涉及到边的延长线部分了。

就好像外角平分线在三角形外面也在按照自己的规则管理着边和角的关系呢。

三角形角平分线关系嘿，咱今儿就来唠唠这三角形角平分线的事儿。

你想想啊，这三角形就好比是咱生活中的一个小团体，那角平分线呢，就是这个团体里的和事佬。

为啥这么说呢？你看啊，角平分线把一个角平分成了相等的两份，就像咱在朋友间调解矛盾，让两边都能得到公平的对待。

有一次我和几个朋友一起研究三角形呢。

我就说：“嘿，你们看这角平分线多有意思，它就像个公平使者。

”朋友小李就接话了：“可不是嘛，它把角分得那么均匀，太神奇了。

”另一个朋友小张也点头说：“对对对，要是咱生活中也有这么个角平分线就好了，啥事儿都能分得妥妥当当的。

”然后我们就开始动手画三角形，画完了就研究那些角平分线。

我指着一个三角形说：“你们瞧，这条角平分线把这个角分成了一样大的两半，多厉害。

”小李就笑着说：“哈哈，要是人的心也能被角平分线这么分一下，那该多好，就不会有那么多偏心啦。

”我们都笑了起来。

在研究的过程中，我们还发现了一些有趣的现象。

比如，角平分线相交的那个点，好像有着特别的魔力。

我们就开始琢磨这个点到底有啥特别的。

小张说：“我感觉这个点就像一个中心枢纽，把整个三角形都给联系起来了。

”我一想，还真是这么回事儿。

经过这么一番研究和探讨，我越发觉得这三角形角平分线有意思极了。

它不仅在数学里有着重要的地位，在咱生活中也能找到类似的道理呢。

咱就说，这角平分线让三角形变得更加有规律，更加有序。

它让每个角都能得到恰当的划分，不会有谁多谁少的问题。

这就像我们在与人相处的时候，要公平公正，不能偏袒一方。

而且，角平分线还让我们看到了数学中的那种和谐之美，几个简单的线条就能让一个图形变得如此有魅力。

所以啊，可别小瞧了这三角形角平分线，它能给我们带来好多启发呢！。

二 由角平分线想到的辅助线口诀：图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等。

对于有角平分线的辅助线的作法，一般有两种。

①从角平分线上一点向两边作垂线；②利用角平分线，构造对称图形（如作法是在一侧的长边上截取短边）。

通常情况下，出现了直角或是垂直等条件时，一般考虑作垂线；其它情况下考虑构造对称图形。

至于选取哪种方法，要结合题目图形和已知条件。

与角有关的辅助线（一）、截取构全等几何的证明在于猜想与尝试，但这种尝试与猜想是在一定的规律基本之上的，希望同学们能掌握相关的几何规律，在解决几何问题中大胆地去猜想，按一定的规律去尝试。

下面就几何中常见的定理所涉及到的辅助线作以介绍。

如图1-1，∠AOC=∠BOC ，如取OE=OF ，并连接DE 、DF ，则有△OED ≌△OFD ，从而为我们证明线段、角相等创造了条件。

例1． 如图1-2，AB//CD ，BE 平分∠BCD ，CE 平分∠BCD ，点E 在AD 上，求证：BC=AB+CD 。

分析：此题中就涉及到角平分线，可以利用角平分线来构造全等三角形，即利用解平分线来构造轴对称图形，同时此题也是证明线段的和差倍分问题，在证明线段的和差倍分问题中常用到的方法是延长法或截取法图1-1B图1-2DBC来证明，延长短的线段或在长的线段长截取一部分使之等于短的线段。

但无论延长还是截取都要证明线段的相等，延长要证明延长后的线段与某条线段相等，截取要证明截取后剩下的线段与某条线段相等，进而达到所证明的目的。

简证：在此题中可在长线段BC 上截取BF=AB ，再证明CF=CD ，从而达到证明的目的。

这里面用到了角平分线来构造全等三角形。

另外一个全等自已证明。

此题的证明也可以延长BE 与CD 的延长线交于一点来证明。

自已试一试。