05 热力学第二定律

解释热力学第二定律
热力学第二定律是热力学中的一个基本定律，也被称为熵增定律。

它提供了一个描述自然界中热现象发生方向的规律。

热力学第二定律有多种表述方式，其中最常见的是克劳修斯表述和开尔文表述。

克劳修斯表述，不可能将热量从低温物体自发地传递给高温物体，而不产生其他效果。

这个表述可以解释为，热量不会自发地从冷的物体转移到热的物体，而不产生其他变化。

例如，我们无法将热量从一个冷水杯中传递到一个热水杯中，而不使用外部能量（如加热器）。

开尔文表述，不可能通过一个循环过程将热量完全转化为功而不产生其他效果。

这个表述可以解释为，不可能通过一个循环过程将热量完全转化为有用的功而不产生其他变化。

换言之，不可能将热量全部转化为有用的能量，而不产生其他形式的能量损失。

热力学第二定律的核心思想是熵的增加。

熵是描述系统无序程度的物理量，热力学第二定律指出，一个孤立系统的熵总是趋向于增加，而不会减少。

换句话说，自然界中的过程总是朝着更高熵（更大的无序）的方向发展。

总结来说，热力学第二定律告诉我们，热现象具有一种不可逆性，热量不会自发地从冷物体传递到热物体，而且热量无法完全转化为有用的功而不产生其他形式的能量损失。

这个定律对于理解自然界中的热现象和能量转化过程非常重要。

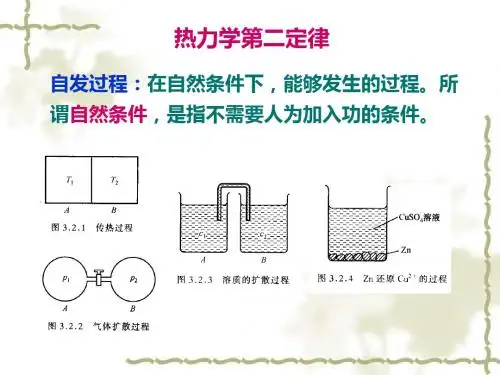
热力学第二定律一、自发反应—不可逆性（自发反应乃是热力学的不可逆过程）一个自发反应发生之后，不可能使系统和环境都恢复到原来的状态而不留下任何影响,也就是说自发反应是有方向性的，是不可逆的。

二、热力学第二定律1.热力学的两种说法：Clausius:不可能把热从低温物体传到高温物体，而不引起其它变化Kelvin：不可能从单一热源取出热使之完全变为功，而不发生其他的变化2.文字表述：第二类永动机是不可能造成的（单一热源吸热,并将所吸收的热完全转化为功)功热【功完全转化为热，热不完全转化为功】(无条件，无痕迹，不引起环境的改变）可逆性:系统和环境同时复原3.自发过程：（无需依靠消耗环境的作用就能自动进行的过程）特征:(1）自发过程单方面趋于平衡；(2）均不可逆性；(3)对环境做功,可从自发过程获得可用功三、卡诺定理(在相同高温热源和低温热源之间工作的热机）（不可逆热机的效率小于可逆热机）所有工作于同温热源与同温冷源之间的可逆机，其热机效率都相同,且与工作物质无关四、熵的概念1.在卡诺循环中，得到热效应与温度的商值加和等于零：任意可逆过程的热温商的值决定于始终状态，而与可逆途径无关热温商具有状态函数的性质：周而复始数值还原从物理学概念,对任意一个循环过程，若一个物理量的改变值的总和为0，则该物理量为状态函数2。

热温商:热量与温度的商3。

熵：热力学状态函数熵的变化值可用可逆过程的热温商值来衡量（数值上相等）4. 熵的性质:(1)熵是状态函数，是体系自身的性质是系统的状态函数，是容量性质（2)熵是一个广度性质的函数，总的熵的变化量等于各部分熵的变化量之和（3）只有可逆过程的热温商之和等于熵变(4）可逆过程热温商不是熵，只是过程中熵函数变化值的度量（5）可用克劳修斯不等式来判别过程的可逆性（6）在绝热过程中，若过程是可逆的,则系统的熵不变（7）在任何一个隔离系统中,若进行了不可逆过程，系统的熵就要增大,所以在隔离系统中，一切能自动进行的过程都引起熵的增大。

热力学第二定律的表述热力学第二定律，也称为熵增定律，是热力学中的重要概念之一。

该定律表明，任何一个孤立系统在自发过程中，其熵总是不断增加的。

熵是一个描述系统无序程度的物理量，可理解为一个系统的混乱程度。

具体来说，热力学第二定律的表述可以从以下几个方面进行阐述：一、热力学第二定律的基本原理热力学第二定律是热力学的基本定律之一，它表明孤立系统总是向着不可逆的方向进行自发变化。

熵作为描述系统无序程度的物理量，可以解释这一现象。

热力学第二定律将熵增作为孤立系统自发性质的概率形式，即熵的增加是不可逆的。

二、熵的定义及熵增过程的表述熵是一个描述系统无序程度的物理量，熵的增加意味着这一系统的混乱程度变得更大，而系统的混乱程度是不可逆的。

热力学第二定律表明，在孤立的系统中，一切自发过程中的熵增加，即系统无序程度不断增大。

这种无序程度的增加可以表述为：在过程中，能量总是从有序的状态流向有限的状态，因此越来越多的能量被转化为无用的热能。

三、热力学第二定律和环境保护的关系热力学第二定律是我们了解和约束自然界不可逆演化过程的基础。

正是热力学第二定律的存在，才有了反渗透、风能、水力发电，甚至太阳能电池等各种环境保护技术。

人类社会发展中不断寻找新的技术，不仅是为了满足能源需求，更重要的是要在这个过程中尽可能地减少环境污染。

总之，热力学第二定律能够为我们揭示自然界中不可逆的演化规律，对于人类社会发展中的环境保护及科学技术的发展，也起到了重要的指导意义。

我们应该加强对这一领域的研究，推进可持续发展进程，使得人类社会发展与环境保护取得良好的平衡。

【5－1】下列说法是否正确？（1）机械能可完全转化为热能，而热能却不能完全转化为机械能。

（2）热机的热效率一定小于1。

（3）循环功越大，则热效率越高。

（4）一切可逆热机的热效率都相等。

（5）系统温度升高的过程一定是吸热过程。

（6）系统经历不可逆过程后，熵一定增大。

（7）系统吸热，其熵一定增大；系统放热，其熵一定减小。

（8）熵产大于0的过程必为不可逆过程。

【解】（1）对于单个过程而言，机械能可完全转化为热能，热能也能完全转化为机械能，例如定温膨胀过程。

对于循环来说，机械能可完全转化为热能，而热能却不能完全转化为机械能。

（2）热源相同时，卡诺循环的热效率是最高的，且小于1，所以一切热机的热效率均小于1。

（3）循环热效率是循环功与吸热量之比，即热效率不仅与循环功有关，还与吸热量有关。

因此，循环功越大，热效率不一定越高。

（4）可逆热机的热效率与其工作的热源温度有关，在相同热源温度的条件下，一切可逆热机的热效率都相等。

（5）系统温度的升高可以通过对系统作功来实现，例如气体的绝热压缩过程，气体温度是升高的。

（6）T QdS δ>>系统经历不可逆放热过程，熵可能减小；系统经历不可逆循环，熵不变。

只有孤立系统的熵只能增加。

系统经历绝热不可逆过程，熵一定增大。

（7）g f dS dS dS +=，而0≥g dS ，系统吸热，0>f dS ，所以熵一定增加；系统放热时，0<f dS ，此时要比较g dS 与f dS 的大小，因此熵不一定减小。

（8）熵产就是由不可逆因素引起的熵增，所以熵产大于0的过程必为不可逆过程。

【5－2】某人声称发明一个循环装置，在热源1T 及冷源2T 之间工作。

若1T =1700K ，2T =300K 。

该装置能输出净功1200kJ ，而向冷源放热600kJ ，试判断该装置在理论上是否由可能。

【解】据能量守恒原理，装置内工质从高温热源吸热net W Q Q +=21=600+1200=1800kJ装置热效率1Q W n e t t =η=18001200=66.67% 在同温限的恒温热源间工作的卡诺循环热效率为121T T c -=η=17003001-=82.35% 比较t η和c η可知，此装置有可能实现，是一不可逆热机。

热力学第二定律热力学第二定律是热力学中的一条重要定律，它描述了自然界中热能传递的方向和过程的不可逆性。

热力学第二定律即卡诺定理，这一定律的发现不仅推动了热力学的发展，也在工程和科学研究中发挥着巨大的作用。

热力学第二定律的核心思想是热能的自发从高温系统向低温系统传递，而不会相反。

这个思想在日常生活中随处可见。

当我们将一杯热茶放置在桌子上，茶的温度逐渐降低，而不会变得更热。

这个过程是不可逆的，它符合热力学第二定律的要求。

热力学第二定律的原型是卡诺定理，它由法国工程师尼古拉·卡诺在19世纪初提出。

卡诺定理表达了理想热机的效率与工作温度之间的关系。

根据卡诺定理，任何机械热机的效率都不可能高于理论上的最大值，即卡诺热机的效率。

卡诺热机是一个在两个不同温度下工作的理想热机，其效率由工作温度之间的比值决定。

这种限制性的不可逆性是热力学第二定律的核心内容，也是热力学与统计物理学的重要区别之一。

事实上，热力学第二定律的发现引发了科学家们对宇宙中热能传递过程的深入研究。

他们发现，自然界中存在着一种名为熵的物理量，它代表了系统无序程度的度量。

根据熵的增加原理，自然倾向于朝着更高熵的方向演化，这就意味着热能应该自发地从高温系统传递到低温系统，而不会相反。

熵增加原理使热力学第二定律更加深入人心，在科学研究和工程设计中得到了广泛应用。

比如，通过了解热力学第二定律，我们可以最大限度地提高能源利用效率，减少能量的浪费。

这对于提升工业生产的效益和降低环境污染具有重要意义。

在工程中，通过设计有效的热回收系统，可以将废热转化为有用的能量，实现能量的再利用。

除了工程应用外，热力学第二定律在生物学中也有深远的影响。

生命系统本质上是开放的非平衡系统，需要从外部吸收能量来维持其复杂的结构和功能。

热力学第二定律为生物学家提供了理论基础，从微观角度解释了生命现象的发生。

通过深入理解热力学第二定律，科学家能够更好地探索生物体内能量转换的机制，从而拓宽我们对生命起源和演化的认识。

热力学第二定律解析热力学第二定律及其与熵的关系热力学第二定律作为热力学基本定律之一，对于研究热力学系统的行为和性质具有重要意义。

它揭示了自然界中一种普遍存在的规律，并与熵这一热力学量密切相关。

本文将对热力学第二定律的核心内容进行解析，并探讨它与熵的关系。

一、热力学第二定律的概念与表述热力学第二定律是描述自然界中热现象发生方向性的基本定律，它有多种表述方式。

其中，开尔文表述是最常见的。

开尔文表述指出，不可能从单一热源中吸热完全转化为可做的功而不引起其他变化的过程。

这意味着热能不会自发地从低温物体传递给高温物体，而只会沿着温度梯度由高温传向低温。

二、热力学第二定律的数学描述除了开尔文表述，热力学第二定律还可以通过数学方式进行描述。

热力学第二定律可以用克劳修斯表述来表达，即热量不会自发地从低熵物体传递到高熵物体。

在这种描述中，熵是一个关键的热力学量，它代表了系统的无序程度或混乱程度。

根据克劳修斯表述，任何孤立系统的熵都不会减少，而是增加或保持不变。

这意味着自然界趋向于朝着更高的熵方向发展，即朝着更大的无序性发展。

三、熵的概念与计算方法熵是描述热力学系统无序程度的物理量，它可以用数学方法进行计算。

熵的计算方法主要有两种：统计熵和宏观熵。

统计熵是基于热力学微观模型和概率统计原理得出的熵计算方法，它涉及到粒子的状态数和相应的概率。

而宏观熵是基于宏观性质和测量结果得出的熵计算方法，它通过物态方程和其他宏观性质来计算系统的熵。

四、热力学第二定律与熵的关系热力学第二定律与熵的关系是热力学研究中的一个重要问题。

根据熵的定义和计算方法，熵的增加可以看作是系统自发朝热平衡状态发展的结果，而热力学第二定律则描述了热现象发生的方向性。

从数学上讲，熵的增加可以用热力学第二定律来解释，即熵的增加是由于热能在温度梯度下自发地从高温物体传递到低温物体，从而使得整个系统的无序程度增加。

因此，熵与热力学第二定律密切相关。

五、实例分析：热机工作过程中的熵增为了更好地理解热力学第二定律和熵的关系，我们可以以热机工作过程为例进行分析。