微波仿真论坛附录COMSOLMultiphysics的MATLAB矢量计算基础18页

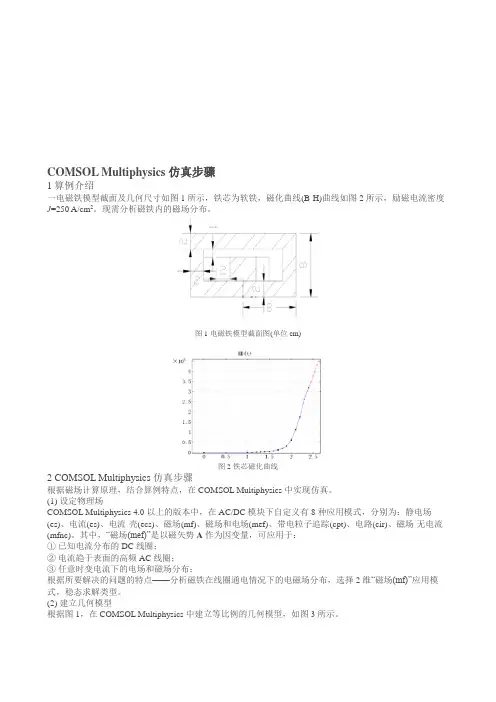
COMSOL Multiphysics仿真步骤1算例介绍一电磁铁模型截面及几何尺寸如图1所示，铁芯为软铁，磁化曲线(B-H)曲线如图2所示，励磁电流密度J=250 A/cm2。

现需分析磁铁内的磁场分布。

图1电磁铁模型截面图(单位cm)图2铁芯磁化曲线2 COMSOL Multiphysics仿真步骤根据磁场计算原理，结合算例特点，在COMSOL Multiphysics中实现仿真。

(1) 设定物理场COMSOL Multiphysics 4.0以上的版本中，在AC/DC模块下自定义有8种应用模式，分别为：静电场(es)、电流(es)、电流-壳(ecs)、磁场(mf)、磁场和电场(mef)、带电粒子追踪(cpt)、电路(cir)、磁场-无电流(mfnc)。

其中，“磁场(mef)”是以磁矢势A作为因变量，可应用于：①已知电流分布的DC线圈；②电流趋于表面的高频AC线圈；③任意时变电流下的电场和磁场分布；根据所要解决的问题的特点——分析磁铁在线圈通电情况下的电磁场分布，选择2维“磁场(mf)”应用模式，稳态求解类型。

(2) 建立几何模型根据图1，在COMSOL Multiphysics中建立等比例的几何模型，如图3所示。

图3几何模型有限元仿真是针对封闭区域，因此在磁铁外添加空气域，包围磁铁。

由于磁铁的磁导率，因此空气域的外轮廓线可以理想地认为与磁场线迹线重合，并设为磁位的参考点，即(21) 式中，L为空气外边界。

(3) 设置分析条件①材料属性本算例中涉及到的材料有空气和磁铁，在软件自带的材料库中选取Air和Soft Iron。

对于磁铁的B-H曲线，在该节点下将已定义的离散B-H曲线表单导入其中即可。

②边界条件由于磁铁的磁导率，因此空气域的外轮廓线可以理想地认为与磁场线迹线重合，并设为磁位的参考点，即(21) 式中，L为空气外边界。

为引入磁铁的B-H曲线，除在材料属性节点下导入B-H表单之外，还需在“磁场(mef)”节点下选择“安培定律”，域为“2”，即磁铁区域，在“磁场 > 本构关系”处将本构关系选择为“H-B曲线”。

1引言使用计算机模拟物理学问题能帮助学生更深刻的理解物理学，帮助学生在学习中了解和掌握使用计算机做物理学研究的一些基本手段，并学会如何根据具体的物理问题选择相应的研究方法[1]。

Comsol Multiphysics 是一款大型的高级数值仿真软件[2]，广泛应用于各个领域的科学研究以及工程计算，模拟科学和工程领域的各种物理过程，Comsol Multiphysics 以高效的计算性能和杰出的多场双向直接耦合分析能力实现了高度精确的数值仿真。

利用Comsol Multiphysics 软件的AC/DC 物理场模块，可以仿真各种形状的电极构成的电流场，能够得到相应的电位分布图像、绘制等位线等，便于学生对静电场以及稳恒电流场的规律进行探究式学习，在实验教学中能起到很好的演示作用，并且根据仿真的结果能对各种电极的实际设计提供参考。

2Comsol Multiphysics 仿真2.1同轴圆柱电极电位分布同轴圆柱电极的电位分布的理论表达式为：U r =U 01n (b /r )1n (b /a )（1）其中a、b 分别为中心电极的半径和外圆环的内半径，U 0为同轴圆柱正负电极的电位差，r 为场点到电极中心轴线的距离。

对于实际测量的电极，其中a=7mm，b=50mm。

水作为导电介质，输入电压U 0=10V。

根据上述实验条件，运行Comsol Multi-physics 5.1软件进行仿真。

在空间维度中选择三维，组件下的几何体选择圆柱体，半径设置为55mm，高度设置为10mm，层1厚度设置为5mm，层2厚度设置为43mm，构建的几何模型如图1所示。

中心圆柱体和外圆环的材料设置为铜，两者之间的材料设置为水。

网格设置序列类型为物理场控制网格，单元尺寸设置为极端细化。

在物理场选项中选择AC/DC的电流（ec ）物理场模块。

设置整个外圆环为接地端，整个中心电极为终端，终端类型为电压，电压设置为10V。

研究选项中选择稳态，经过软件计算后电流场的电位分布以颜色图例显示出来，等位线分布如图2所示。

COMSOL与MATLAB联合仿真的实现方法作者：赵晓磊齐秋菊郭春超来源：《中国新技术新产品》2014年第24期摘要：本文在分析COMSOL与MATLAB这两款软件特点的基础上，研究了COMSOL 与MATLAB联合仿真的方法，通过COMSOL与MATLAB之间的相互调用，实现了MATLAB与COMSOL的数据传递，并结合实例介绍了联合仿真的方案，通过这两款软件的联合仿真，提高了仿真效率。

关键词：联合仿真；COMSOL；MATLAB中图分类号：TP31 文献标识码：ACOMSOL Multiphysics是一款大型的高级数值仿真软件。

广泛应用于各个领域的科学研究以及工程计算，被称为“第一款真正的任意多物理场直接耦合分析软件”。

在模拟科学和工程领域的各种物理过程中，COMSOL以高效的计算性能和杰出的多场双向直接耦合分析能力实现了高度精确的数值仿真。

COMSOL是以有限元法（FEM）为基础，通过求解偏微分方程来实现真实物理现象的仿真。

目前已经在声学、生物科学、化学反应、电磁学、流体动力学、燃料电池、地球科学、热传导、光学等领域得到了广泛的应用。

尽管COMSOL在仿真方面能力强大，但是由于软件没有可以输入程序的功能，使COMSOL对于进行大量重复性工作时，如果全由人工进行，工作量非常大。

而COMSOL其实是起源于MATLAB的Toolbox，最初命名为Toolbox 1.0。

因此这两款软件之间相互兼容，可以联合起来进行仿真。

这样，利用 MATLAB 进行编程，实现COMSOL的建模、计算、后处理等工作。

1 COMSOL与MATLAB 联合仿真的实现方案1.1 COMSOL 与MATLAB 联合仿真环境的连接方式本文采用的软件是Matlab2011b和COMSOL 4.3，系统为Win7，64bit。

安装顺序为先安装MATLAB，然后安装COMSOL到MATLAB的子文件夹下，并勾选link to MATLAB选项。

COMSOL Multiphysics 有限元法多物理场建模与分析序 言多物理场耦合模型及数值模拟在各领域的研究及应用正在快速地发展。

本书的读者可通过如下方式获得实用的信息，新的期刊、国际多物理场期刊(/)和ComsolMultiphysics 软件包()，同时可以访问中文网站( )以获取更多的中文资料及在线的视频教程，Comsol 软件对于复杂过程的耦合建模能力给用户呈现了广阔的应用空间。

本书整理了我近年来对Comsol Multiphysics 软件的应用体会，同时我也随着软件一起“成长”。

我最早的博士研究生中有一位在1995 年就开始使用Matlab 软件的PDE toolbox，该工具箱也就是ComsolMultiphysics (原Femlab)软件的前身，用于开发多相流电容层析成像重建算法。

我们早在2001 年就购买了Femlab 2.0 软件，她对有限元建模具有卓越的图形用户界面和扩充功能，我们用她来处理电动流和微通道流的混合。

我于2002 年六月首次提供了基于Femlab 2.2 的加强模块，随着一系列的深入技术交流，她最终发展为有限元方法的过程建模和仿真。

自从我们开发了更为有效的模块以及新模块实例，这个模块已经运行过八次，每一模块都引入了新的功能，并且我的研究团队已学会如何使用。

随着2005 年Comsol Multiphysics 3.2 的引进，Femlab 根本的改革牢牢地集中在多物理场模型建立的准确定位。

图形用户界面的操作界面以及给人的感觉已经改变了，所以很多对Femlab 一步一步的描述不再和现代软件版面设计相匹配。

处理例子的最好方法也不再是最初我用Femlab 的方法。

我们的许多模型是对Matlab代码生成的混合GUI 应用，随后是基本Matlab 程序设计步骤。

Comsol Multiphysics 的GUI 中新的内建工具和许多新特征一起给出了足够的功能，那些对Matlab 程序设计不是特别需要的。

Comsol和Matlab 联合仿真的⽅法
1.联合使⽤Comsol和Matlab的原因：
尽管Comsol在仿真⽅⾯能⼒强⼤，但是由于软件没有可以与ANSYS⼀样输⼊程序的功能，使Comsol对于进⾏⼤量重复性⼯作时，如果全由⼈⼯进⾏，⼯作量⾮常⼤。

⽽COMSOL其实是起源于MATLAB的Toolbox的，最初命名为Toolbox 1.0。

这两款软件，可以联合起来进⾏仿真。

这样，利⽤MATLAB强⼤的计算功能，可以实现通过MATLAB进⾏编程，实现Comsol的建模，计算，后处理等⼯作。

sol与matlab联合仿真的实现：
所⽤软件为Matlab2011b和Comsol 4.2,系统为win7，64bit。

安装顺序为先安装Matlab，然后安装Comsol到Matlab的⼦⽂件夹2011b\bin\win64下，并勾选link to matlab选项，地址为2011b⽂件夹。

安装完毕后，打开Comsol with matlab,会打开matlab界⾯，然后⼿⼯打开Comsol。

这两个软件就通过⼀个共同的服务器联系在⼀起了。

sol 和Matlab相互调⽤的⽅法：
Matlab调⽤Comsol模型⽂件：对于Comsol中已经建好的某个模型，将其保存为Matlab可调⽤的.M格式⽂件，然后在Matlab的⼯作路径⾥找到这个⽂件并打开即可；
Comsol调⽤Matlab模型⽂件：对于Matlab中通过M语⾔已经编好的M模型⽂件，运⾏（Run），在Comsol的File下找到“从服务器导⼊模型”即可。

Matlab 与Feko软件混合目录•概述•模型的建立•EditFeko中控制卡的编辑•Matlab调用Feko 讨论•Matlab对Feko结果文件的处理Matlab调用Feko的几个要点•Matlab调用Feko的几个要点–在Matlab以如下形式调用Fekodos('prefeko OnespiralAnt');dos (‘runfeko OnespiralAnt');其中的OnespiralAnt为Feko工程文件的名称，prefeko和runfeko是Feko关键字符串，分别表示Feko预处理和Feko求解器–在Feko中生成的.pre和.out可以以文本的形式打开，所以在Mablab中可以象处理文本那样来处理这些文件：在Matlab定义一个变量，该变量对应于Feko的.pre文件中某一个变量（如：工作频率、几何模型的尺寸变量、模型旋转角等），这样，就可以用Matlab控制Feko中的这个变量，每改变一次该变量的值就可以重新生成一个新的.pre文件，然后调用runFeko运行新生成的.pre文件；同样，可以应用Matlab像处理文本一样来处理Feko的结果文件.out，来对仿真结果进行处理。

–Matlab生成的.m文件需要和Feko的工程文件、.pre文件及输出文件存放在同一文件夹中。

举例（单螺旋天线）•问题描述–以单螺旋为例来说明如何用Matlab控制Feko•可以在CadFeko中进行建模；•也可以在EditFeko中进行建模；（有些问题用EditFeko处理会非常方便）–Matlab可以控制Feko脚本文件.pre中的某个或某几个变量，在该例子中是控制螺旋天线的旋转角度#alpha–Matlab控制Feko的结果文件（.out）,（要想很好的处理结果文件，必须对其格式非常清楚）读取内部的源阻抗数值目录•概述•模型的建立•EditFeko中控制卡的编辑•Matlab调用Feko 讨论•Matlab对Feko结果文件的处理螺旋天线的建立（CadFeko）•建立Feko工程文件“OneSpiralAnt”•双击Variables添加以下变量：freq=3.0e+10n=6.5, lambda=c0/freqD=lambda/pi,s=0.225*lambda,seg_len=lambda/15seg_rad=lambda/200tri_len=lambda/20.0a=0.75*lambda•点击图标添加螺旋曲线helix•点击图标把helix模型分成两部分选择小的一部分更名为：feed模型建立•点击图标创建地板ground网格剖分•选中所有模型点击图标进行模型合并，并把新生成的模型更名为spiral •把馈源位置的线元更名为feed•点击菜单“Mesh\create mesh”或按住键盘Ctrl+M进行网格剖分目录•概述•模型的建立•EditFeko中控制卡的编辑•Matlab调用Feko 讨论•Matlab对Feko结果文件的处理EditFeko处理•按住Alt+2进行预处理，并保存工程文件•按住Alt+1调出EditFeko•在IN卡下边添加FM卡•在FM卡下边添加“#alpha=0”•然后添加TG卡** TG卡用来控制模型的平移与旋转，在该项目中，我们是把该基本模型沿y轴旋转#alpha角度，初始值是0度•修正FR卡•添加A1卡•添加FF卡•所有的控制卡添加完毕后保存该文件Spiral.feed目录•概述•模型的建立•EditFeko中控制卡的编辑•Matlab调用Feko 讨论•Matlab对Feko结果文件的处理Matlab部分处理•点击Matlab程序中的M-file editor或先进入Matlab主程序，在主程序中点击菜单“File\New\M file”进行.m文件的制作部分（可以命名为OneSpiralAnt.m）•第一步添加如下命令clear all; %清除工作间的变量和函数•第二步添加循环（该循环的目的是为了得到不同的旋转角alpha，循环变量用i表示，i的变化范围是从1到5，步长为1，alpha表示为10*i）for i=1:1:5第一部分：初始化变量部分；第二部分：文件的读写部分；第三部分：生成新的脚本文件；第四部分：Matlab中调用Feko；end % 结束for循环•第一部分：变量的初始化special_str_1='prefeko ';special_str_2='runfeko ';project_name=' OneSpiralAnt_';prestr='#alpha='; % Initialise a variable for special string注释：变量special_str_1、special_str_2和project_name是为了最终装配最终的字符串形式“runfeko OneSpiralAnt_1.pre”而设定的，因为在循环中，我们是以OneSpiralAnt_1.pre、OneSpiralAnt_2.pre…OneSpiralAnt_5.pre的形式来存储脚本文件的，而且每循环生成一个.pre脚本文件，我们会运行一次Feko软件，这样处理就相对比较灵活了prestr变量是一个关键字符，用于存储模型的旋转角度•第二部分：文件的读写部分fid_r=fopen(‘OneSpiralAnt.pre’,‘r’); % Define a file reading point （定义读文件指针）fid_w=fopen(‘OneSpiralAnt.tmp’,‘w’); %Define a file writting point （定义写文件指针）while ~feof(fid_r) % while not the end of the file （如果不是文件的结尾就继续循环）line_r=fgetl(fid_r); % get each line value （遍历每一行的值）g=strfind(line_r,‘#alpha=’); % whether this line need be modified（是否是需要修改的那一行）if g>0 %如果是需要修改的那一行，则在if…end区间修改这一行的值newvalue=num2str(10*(i-1));line_r=strcat(prestr,newvalue); % modify this line's value, line_r=‘#alpha=10’or 20…end% 通过fprintf语句把line_r的值写入fid_w指向的文件OneSpiralAnt.tmp中fprintf(fid_w,'%s\n',line_r); % write each line to the file 'OneSpiralAnt.tmp' end %end while （结束读写脚本文件循环）fclose(fid_r); % close file reading point (关闭读文件指针)fclose(fid_w); % close file writting point (关闭写文件指针)•第三部分：生成新的脚本文件% get and save each .pre file in the form of OneSpiralAnt_1.pre,OneSpiralAnt_2.pre...% 我们需要生成的文件的名称分别为OneSpiralAnt_1.pre,OneSpiralAnt_2.pre,OneSpiralAnt_3.pre, % OneSpiralAnt_4.pre以及OneSpiralAnt_5.pre% new_file_name分别为OneSpiralAnt_1.pre, OneSpiralAnt_2.pre, OneSpiralAnt_3.pre…new_file_name=strcat('OneSpiralAnt_',num2str(i));new_file_name=strcat(new_file_name,'.pre');% 把文件OneSpiralAnt.tmp中的内容拷贝到new_file_name中，即生成上边提到的5个.pre文件中copyfile('OneSpiralAnt.tmp',new_file_name);•第四部分：Matlab调用Feko% Assemble the “prefeko OneSpiralAnt_i.pre”stringsspecial_str_1=strcat(special_str_1,project_name);special_str_1=strcat(special_str_1,num2str(i));special_str_1=strcat(special_str_1,'.pre');% Assemble the “runfeko OneSpiralAnt_i.pre”stringsspecial_str_2=strcat(special_str_2,project_name);special_str_2=strcat(special_str_2,num2str(i));special_str_2=strcat(special_str_2,'.pre');%invoke feko functions (通过dos函数调用prefeko、funfeko)dos(special_str_1); % dos(‘prefeko OneSpiralAnt_1.pre')dos(special_str_2); % dos('runfeko OneSpiralAnt_1.pre')%;完整的Matlab代码结果文件分析•打开Matlab 主程序，调出OneSpiralAnt.m 文件，然后点击菜单Debug\Run 或直接按F5开始运行，运行完毕后，•我们就得到了5个后缀为.pre 的脚本文件，5个PostFeko 文件（后缀为.bof,.fek ）以及5个后缀为.out 的结果文件，它们分别对应不同的角度alpha ，分别打开*_1.fek, *._2.fek, *_3.fek,*_4.fek 和*_5.fek 可以看到模型随角度的变化alpha=0alpha=10alpha=20alpha=30alpha=40EditFeko文件中alpha 角度的变化alpha=0alpha=40 alpha=10alpha=20alpha=30目录•概述•模型的建立•EditFeko中控制卡的编辑•Matlab调用Feko 讨论•Matlab对Feko结果文件的处理•借用前边的项目文件OneSpiralAnt.cfx,OneSpiralAnt.cfm和OneSpiralAnt.pre。

功能强⼤的多物理场耦合分析软件功能强⼤的多物理场耦合分析软件COMSOL Multiphysics（原FEMLAB）COMSOL Multiphysics是⼀个专业有限元数值分析软件包，是对基于偏微分⽅程的多物理场模型进⾏建模和仿真计算的交互式开发环境系统。

它为所有科学和⼯程领域物理过程的建模和仿真提供了⼀种崭新的技术！COMSOL Multiphysics的多物理场问题⼀次轻松解决，让您⼀次就能轻松拥有超强功能、超低价格的CAE 软件。

COMSOL Multiphysics是专为描述和模拟各种物理现象⽽开发的基于有限元分析的软件包，它使得建⽴各种物理现象的数学模型并进⾏数值模拟计算变得更为容易和可能。

在使⽤COMSOL Multiphysics软件的过程中，您可以⾃⼰建⽴普通的偏微分⽅程形式，也可以使⽤COMSOL Multiphysics提供的特定的物理应⽤模型。

这些特定的物理应⽤模型包括预先设定好的模块和在⼀些特殊应⽤领域已经通过微分⽅程和变量建⽴起来的⽤户界⾯。

此外，COMSOL Multiphysics软件通过把任意数⽬的这种物理应⽤模块整合成对⼀个单⼀问题的描述，使得建⽴耦合问题变得更为容易。

模型库是整个COMSOL Multiphysics软件包的最特⾊部分，它囊括了各种⼯程领域的所有模型。

每⼀个模型都包含了⾮常完善的相关⽂档如⼯程技术背景、结果讨论和⼀步⼀步建⽴模型的每个过程描述。

由于这些模型⽂件都已经包括了⽹格划分和运⾏计算的信息，所以您可以⾃⼰打开这些⽂件并试着进⾏相应的各种后处理操作和显⽰。

另外，您可以应⽤、扩充或者修改这些⼯程模型使它们符合您的个⼈需求。

因此，进⼊这些模型库就给您提供了建⽴⾃⼰模型的基础和起点。

⽽事实上，这些模型库也会给您建⽴⾃⼰的模型提供宝贵的参考。

能够独⽴于MATLAB运算的COMSOL Multiphysics软件系统为进⼀步改进软件提供了⼀个很好的基础和平台。

COMSOL Multiphysics V42a隆重发布新版本新模块新功能COMSOL Multiphysics V4.2a亮点简介COMSOL Multiphysics在多物理场仿真模拟和分析领域已经建立了快速革新的的良好信誉。

最新的4.2a版本在COMSOL Multiphysics旗舰产品成功史上添加了新的一笔。

通过引入工程师和科学家们感兴趣的新功能，COMSOL正在创造一个在广度和深度无与伦比的集成分析平台。

在4.2a版本中主要的创新点如下：粒子追踪模块在CFD，电磁，声学和其他应用领域，追踪粒子和物理场之间的相互作用。

Creo™ Parametric实时链接与PTC™公司最新的设计软件进行无缝双向的CAD集成。

更快速和高效的参数化扫描对于大量的参数化扫描控制内存的使用，并能够快速建立响应图。

导入数字高程图(DEM)导入拓扑表面数据，并结合到固体区域中，用于诸如流体，结构、或电磁等各种物理场的分析。

导入图像基于照相数据或者扫描数据，以材料查找表的形式导入2D图像。

交互式切片图和等值面图绘制面图和切片图时进行快速交互式定位。

磁勘探是一种铁矿勘探中常用的地质学勘探方法。

这幅图片显示了根据导入的地形数据模拟所表征的地下几何结构。

被动式磁勘探于精确的区域性磁异常图形。

本案例求解铁矿在地磁场作用下产生地表和空中的磁异常图形。

粒子追踪模块粒子追踪模块扩展了COMSOL Multiphysics在流场或电磁场中的轨迹计算功能，包括粒子与物理场之间的相互作用。

所有模块都可以和粒子追踪模块进行无缝结合，可以引入驱动粒子运动的额外的建模工具和物理场。

质谱仪用来分离和鉴别中的不同物质，广泛应用于材料工程和环境科学。

本图显示在一个四极透镜中不同分子量的离子的运动轨迹。

电场中同时包含直流和交流部分，这是实现质谱仪功能的要素。

本例模拟计算了石英粒子通过一个静态混合器的轨迹。

由于粒子具有质量，只有一定数量的粒子能到达出口，这可以通过后处理来得到，还可以计算传递属性。

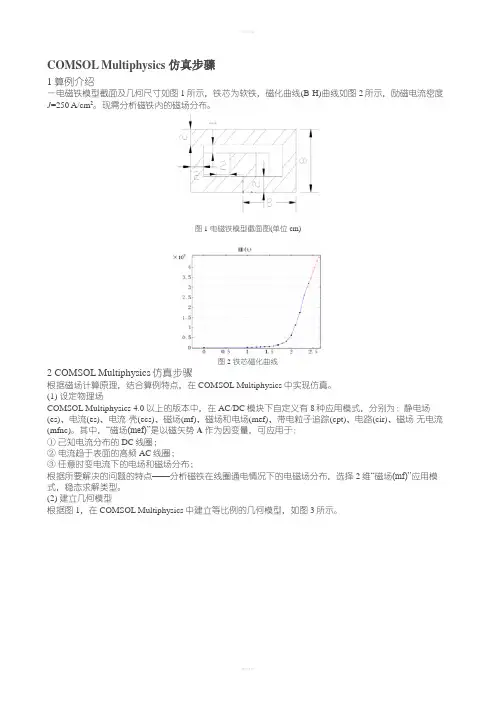
COMSOL Multiphysics仿真步骤1算例介绍一电磁铁模型截面及几何尺寸如图1所示，铁芯为软铁，磁化曲线(B-H)曲线如图2所示，励磁电流密度J=250 A/cm2。

现需分析磁铁内的磁场分布。

图1电磁铁模型截面图(单位cm)图2铁芯磁化曲线2 COMSOL Multiphysics仿真步骤根据磁场计算原理，结合算例特点，在COMSOL Multiphysics中实现仿真。

(1) 设定物理场COMSOL Multiphysics 4.0以上的版本中，在AC/DC模块下自定义有8种应用模式，分别为：静电场(es)、电流(es)、电流-壳(ecs)、磁场(mf)、磁场和电场(mef)、带电粒子追踪(cpt)、电路(cir)、磁场-无电流(mfnc)。

其中，“磁场(mef)”是以磁矢势A作为因变量，可应用于：①已知电流分布的DC线圈；②电流趋于表面的高频AC线圈；③任意时变电流下的电场和磁场分布；根据所要解决的问题的特点——分析磁铁在线圈通电情况下的电磁场分布，选择2维“磁场(mf)”应用模式，稳态求解类型。

(2) 建立几何模型根据图1，在COMSOL Multiphysics中建立等比例的几何模型，如图3所示。

图3几何模型有限元仿真是针对封闭区域，因此在磁铁外添加空气域，包围磁铁。

由于磁铁的磁导率，因此空气域的外轮廓线可以理想地认为与磁场线迹线重合，并设为磁位的参考点，即(21) 式中，L为空气外边界。

(3) 设置分析条件①材料属性本算例中涉及到的材料有空气和磁铁，在软件自带的材料库中选取Air和Soft Iron。

对于磁铁的B-H曲线，在该节点下将已定义的离散B-H曲线表单导入其中即可。

②边界条件由于磁铁的磁导率，因此空气域的外轮廓线可以理想地认为与磁场线迹线重合，并设为磁位的参考点，即(21) 式中，L为空气外边界。

为引入磁铁的B-H曲线，除在材料属性节点下导入B-H表单之外，还需在“磁场(mef)”节点下选择“安培定律”，域为“2”，即磁铁区域，在“磁场 > 本构关系”处将本构关系选择为“H-B曲线”。

基于COMSOL Multiphysics的目标磁特性仿真分析作者：孙晓永张琦潘孟春陈棣湘翁飞兵万成彪来源：《中国测试》2017年第01期摘要：针对潜艇等薄壳类磁性目标的磁场仿真问题，提出基于COMSOL Multiphysics有限元软件的多模型磁场仿真方法。

首先对比分析空心球体模型磁场的理论计算值和仿真值，相对误差优于1%，验证采用该仿真方法解决薄壳物体磁场的准确性。

然后将潜艇等效为空心圆柱体模型，通过COMSOL软件仿真得到其磁场的大小和分布，其中400m处磁场为nT级，在目前磁传感器的探测精度以内。

最后在同一坐标系下建立探测飞行模型，包括潜艇和飞机几何体。

采用离散取点的仿真方法实现多目标模型磁场的仿真，仿真结果与单潜艇模型下基本一致，相似度达到95%，对磁目标探测仿真具有一定的借鉴意义。

关键词：COMSOL Multiphysics软件；仿真方法；磁场分布；目标探测文献标志码：A 文章编号：1674-5124（2017）01-0122-05收稿日期：2016-06-13；收到修改稿日期：2016-08-13基金项目：国家自然科学基金项目（51175507）作者简介：孙晓永（1992-），男，山东聊城市人，硕士研究生，专业方向为电磁测量与传感。

引言潜艇是现代海军隐蔽性最强的装备体系，以广阔海洋为掩护的潜艇广泛应用于战场后，已成为现代战争中，对世界各国军舰队和水上船只极具威胁的突袭手段[1]。

而及时有效地发现敌方潜艇是建立反潜作战系统的先决条件之一，也是在战争中取得优势地位的关键所在[2]。

由于潜艇为铁磁性物体，会对地磁场环境产生异常，故可以采用磁异常探测技术对潜艇进行目标探测和定位识别；并且合理的磁场异常探测技术可以提高探测的精度、效率以及准确度[3]。

目前国内外经常使用的方法是在飞行载体平台上安装基于总量的磁传感器来对其探测范围内的海域进行探测，通过磁异信号来发现潜艇。

探测原理是利用潜艇的磁场信号，对潜艇进行准确定位，并依此解算出目标潜艇的运动要素，及其与飞机的相对位置等参数[4]。

comsol仿真案例Comsol仿真案例。

在工程领域，仿真技术扮演着越来越重要的角色。

Comsol Multiphysics作为一款多物理场仿真软件，被广泛应用于各种工程领域，如电子、光学、声学、热力学等。

本文将介绍一个基于Comsol Multiphysics的仿真案例，以展示其在工程实践中的应用。

我们选择了一个热传导问题作为仿真案例。

假设我们需要设计一个具有特定热传导特性的材料结构，以满足某种工程需求。

在这种情况下，我们可以利用Comsol Multiphysics进行热传导仿真，以验证设计方案的可行性。

首先，我们需要建立仿真模型。

在Comsol Multiphysics中，我们可以通过几何建模模块构建材料结构的几何形状，然后定义材料的热传导特性。

接下来，我们需要设置边界条件和初始条件，以模拟材料结构在特定工况下的热传导行为。

然后，我们可以进行仿真计算。

Comsol Multiphysics提供了强大的求解器，可以有效地求解多物理场耦合问题。

通过设置仿真参数和求解选项，我们可以对材料结构的热传导行为进行精确的数值模拟。

在仿真计算完成后，我们可以对结果进行后处理分析。

Comsol Multiphysics提供了丰富的后处理功能，可以直观地展示仿真结果，如温度分布、热通量、热传导路径等。

通过对仿真结果的分析，我们可以评估设计方案的优劣，并进行必要的优化调整。

通过以上仿真案例，我们可以看到Comsol Multiphysics在工程实践中的重要作用。

它不仅可以帮助工程师们快速准确地验证设计方案，还可以为工程问题的解决提供有力的支持。

因此，Comsol Multiphysics已经成为许多工程领域不可或缺的仿真工具之一。

总的来说，通过本文介绍的Comsol仿真案例，我们可以更好地了解和认识这款多物理场仿真软件在工程实践中的应用。

希望本文能够对工程领域的从业人员有所帮助，也希望Comsol Multiphysics在未来能够为更多工程问题的解决提供支持和帮助。

[转载]Comsol和Matlab联合仿真
1、建立模型
可以在Comsol中先建立好模型或者执行一些操作，然后再通过菜单“文件”->“另存为模型M文件”，查看M文件中的语句，即可了解相应的操作过程和Matlab调用语法；
例：
上面的这个例子，在Comsol中新建了一个3维模型的稳态分析，将单位设置为mm，几何模型中建立了一个长方体，宽度100，深度50，高度10。

基本上通过函数的命名即可看出其实际的意义。

倒数第二句mphgoem函数的作用是在Matlab的Figure中显示几何模型。

打开桌面上的“COMSOL 4.2 with MATLAB”快捷方式，然后运行上述代码，即可看到如下结果：
2、设置材料
设置材料也可以在Comsol中先设置好，然后再另存为模型M文件，下面代码将上述模型材料设置为铝，对于结构分析来说其实关键设置杨氏模量、泊松比和密度就可以了；
3、划分网格
划分网格并显示的代码如下（自由划分网格）：
其中mphmesh函数是显示划分的网格，结果如下：
4、设置载荷和约束
本例约束长方体的下表面，设置体载荷重力载荷，重力方向为Z 轴负方向，设置代码如下：
设置约束时需要选择约束的位置，上面的第二行代码中的[3]为长方体下表面的编号。

5、求解
求解的代码如下：
最后的mphplot函数的作用是在Matlab的Figure中显示分析结果，如下所示：
问题：最终显示结果默认是Von Mises应力的云图，如何设置单独显示变形的云图？结果数据如何导出？
通过为知笔记发布。

基于comsol multiphysics的有限元仿真分析在《固体中的超声导波》教学中的应用
固体中的超声导波是一个重要的物理现象，它在科学研究和工程应用中都有广泛的应用。

随着计算机技术的发展，有限元仿真分析方法越来越得到广泛的应用，而comsol multiphysics是一个能够仿真多物理场和多物理过程的软件平台，其强大的计算功能和可视化表示深受业界的青睐。

本文主要讨论了基于comsol multiphysics的有限元仿真分析在固体中的超声导波教学中的应用。

超声波是在介质中传播的时间变化的振动，它的传播由该介质的本质特性决定，当一个静止的能量源所产生的超声波穿过固体时，它会在此介质中发生变形和反射。

而comsol multiphysics可以仿真多物理量的耦合和传播，通过添加物理模型，可以很好地模拟出固体中超声波反射、传播和衰减等物理现象。

凭借强大的计算能力，comsol multiphysics可以实现复杂场景下的精确仿真，可以用于固体超声传播模型的制作和评估。

基于comsol multiphysics的有限元仿真分析可以实现对不同的材料参数的实时修改和介质结构的准确模拟，它还可以研究超声波在材料内的反射、衰减特性及其介质效应等。

有限元仿真分析为研究复杂材料结构和多物理量耦合现象提供了极大的帮助，因此，它在固体中的超声导波教学是非常有价值的。

总之，comsol multiphysics是一款功能强大的软件，它可以实现精确的多物理仿真，对于固体中的超声导波教学具有重要的参考价值。

它不仅可以提供准确的模拟结果，而且还可以帮助学生理解超声传播的基本原理和机理。

如果说matlab在解偏微分方程时，性能不佳，那么comsol则很好地互补上了。

当然，更好的消息就是这两个软件的连接比较简单，互相调用方便。

/view/656888.htmCOMSOL公司是全球多物理场建模与仿真解决方案的提倡者和领导者，其旗舰产品COMSOL Multiphysics，使工程师和科学家们可以通过模拟，赋予设计理念以生命。

它有无与伦比的能力，使所有的物理现象可以在计算机上完美重现。

COMSOL的用户利用它提高了手机的接收性能，利用它改进医疗设备的性能并提供更准确的诊断，利用它使汽车和飞机变得更加安全和节能，利用它寻找新能源，利用它探索宇宙，甚至利用它去培养下一代的科学家。

COMSOL Multiphysics起源于MATLAB的Toolbox，最初命名为Toolbox 1.0。

后来改名为Femlab 1.0（FEM为有限元，LAB是取自于Matlab），这个名字也一直沿用到Femlab3.1。

从2003年3.2a版本开始，正式命名为COMSOL Multiphysics。

一看这两软件这么有渊源，就知道联合仿真，有戏。

具体实现步骤如下1.系统配置32位win7，matlab2011b，comsol4.2安装comsol时候，有一步骤中要选择matlablive，然后点进去修改matlab的目录，要到bin目录，这样安装完之后，桌面上会多出来一个快捷方式COMSOL 4.2 withMATLAB ，如图所示。

如果第一次安装时候没注意，那么可以重新运行安装程序，选择修复即可。

2.双击COMSOL 4.2 with MATLAB此时弹出一个黑色的框，这个是java的框？不太清楚，不过不用管，最小化就是。

然后matlab会自动启动，并且启动后会弹出几行字，如图所示3.此时在matlab中输入一些命令就可以调用comsol了！例如输入import sol.model.*import sol.model.util.*model = ModelUtil.create('Model');model.modelPath('D:\Program Files\MATLAB\halleyhit');model.modelNode.create('mod1');model.geom.create('geom1', 3);model.mesh.create('mesh1', 'geom1');model.physics.create('es', 'Electrostatics', 'geom1');等等，就是在comsol中建立一些模型，话一些形体，然后可以再加边界条件，加求解范围，开始求解，显示结果等等等等。